Всем привет! Разработка медленно продолжается и я внес достаточно важные изменения в ядро передвижения, так же появилась новая версия платы управления. В результате гексапод теперь умеет выравнивать свое тело благодаря наличию акселерометра и возросла скорость передвижения. Все технические подробности в статье. Как всегда, вас ждет фото и видео.
Github: https://github.com/NeoProg2013/AIWM_hexapod (активная ветка: strain_gauge)
Этапы разработки:
Часть 1 — проектирование
Часть 2 — сборка
Часть 3 — кинематика
Часть 4 — математика траекторий и последовательности
Часть 5 — электроника
Часть 6 — переход на 3D печать
Часть 7 — новый корпус, прикладное ПО и протоколы общения
Часть 8 — улучшенная математика передвижения
Часть 9 — завершение версии 1.00
Часть 10 — датчики касания
Часть 11 — стабилизация
Немного об изменениях в железе
Появилась новая версия платы управления, на этот раз в синем цвете (надоел зеленый). На ней я разместил дополнительный 3V3 стабилизатор напряжения для питания камеры. Так же появились дополнительные разъемы для датчиков касаний, акселерометра и FTDI для реализации терминала в будущем.

Появился вспомогательный микроконтроллер STM32F030, находится он снизу и занимается сбором и обработкой информации с MPU6050 и шести датчиков касания на базе HX711. Он периодически передает результаты обработки данных с датчиков по USART на скорости 1Мбит\с в основной контроллер. В целом на него возложена работа с датчиками, которые только косвенно относятся к ядру передвижения и ядро без этих датчиков будет работать отлично. Я решил вынести это в отдельный МК, чтобы не усложнять логику основного — пусть там будет только ядро передвижения и нечего лишнего. В будущем это открывает возможность кастомизации -- меньше стоимость, меньше функционала.
Например: если убрать датчики касания, то можно сэкономить порядка 2-3к рублей, что достаточно неплохо.
Для общения с HX711 потребовался 8-канальный преобразователь уровней 3V3-5V0. Весь необходимый функционал пока влезает в двухслойную печатную плату, но места для маневров уже остается мало. К счастью, сейчас Китай предлагает производство четырехслойной печатной платы за очень хорошие цены и в будущем это не сильно повлияет на стоимость гексапода.

На плате предусмотрены радиаторы для отвода тепла от стабилизаторов. В корпусе гексапода стоят 2 вентилятора 30х30 для охлаждения силовых DC-DC, плата управления располагается над вентиляторами и при всасывании воздуха внутрь корпуса охлаждается и плата управления.
Стабилизация. Железо
Стабилизация является очередным шагом для реализации адаптации к ландшафту. Гексапод, к сожалению, не умеет как пауки цепляться за стены, поэтому ему нужно выравнивать свое тело для сохранения устойчивости.
Для реализации стабилизации необходимо как-то получить углы наклона тела гексапода в пространстве в текущий момент времени. Для этих целей очень хорошо подходит широко известный MPU6050, стоит копейки, работать с ним просто.

Он имеет на борту акселерометр и гироскоп, а так же Digital Motion Processor. Вот за наличие DMP я и люблю его. DMP это процессор, который не имеет энергонезависимой памяти и в него нужно каждый раз заливать код по I2C. К сожалению, это код никак не документирован и остается надеяться, что он работает как надо (аномалий не замечал ни разу). Засада с ним заключается в его FIFO буфере — его размер не кратен размеру пакета с данными, который в него кладется. Соответственно, при переполнении FIFO часть данных пропадет и все последующие данные будут повреждены. Поэтому частота опроса MPU6050 должна быть выше частоты работы DMP, мы же не хотим допустить переполнения.
DMP позволяет уйти от фильтраций показаний акселерометра и гироскопа, а так же позволяет забыть о компенсации дрейфа гироскопа. На выходе DMP кватернионы, из которых после нехитрых вычислений можно получить нужные нам углы наклона по осям Х и Y, их мы и будем фильтровать. Максимальная частота опроса DMP — 200Hz. Этой частоты более чем достаточно для реализации стабилизации.
Драйвер для MPU6050 с DMP можно взять с моего github. Вам только нужно подсунуть ему библиотеку I2C и заменить функции чтения\записи на свои.
Код DMP и процедура его инициализации были получены путем reverse engineering демонстрационной платы. Большое спасибо людям, которые потратили большое количество времени, чтобы сделать этот код доступным для использования!
Стабилизация. Математика
Начнем с ответа на вопрос "А с чего начать?". А начать нужно с определения метода выравнивания тела. Введем несколько обозначений. На картинке ниже показан идеальный вариант положения конечностей гексапода и земли (черная линия). Кругами обозначена нагрузка на приводы, в данном случае нагрузка распределена равномерно на обе стороны.

В реальности же земля имеет некий наклон и выглядит это следующим образом:

В результате этого на правые приводы возрастает нагрузка за счет изменения распределения массы в правую часть, а в левой части нагрузка уменьшается. На маленьких углах влияние наклона незаметно, но на больших приводы оказываются перегружены и они явно не рады этому. Может показаться, что крайний левый привод тоже должен быть нагружен, т.к. гексапода тянет в бок, но нет. Левая сторона оказывается недогруженной, и левая нога начинает проскальзывать.
Нужно каким-то образом выровнять корпус, чтобы как можно больше веса переместить в противоположную наклону сторону. Есть 2 варианта реализации этого.
Первый вариант заключается в поднимании ног на правой стороне и опусканием на левой на одинаковое расстояние. Данный способ простой в плане расчетов -- просто используем уравнение плоскости, которая проходит через точку (0;0;0) и перпендикулярна вектору наклона тела гексапода.
Но в нашем случае он не подходит. Дело в том, что мы не можем бесконечно опускать конечность, т.к. гексапод когда-нибудь ляжет на брюхо. Да и в целом уменьшать клиренс мысль не очень, это сильно ограничит проходимость.

Есть другой вариант: вместо синхронного опускания\поднимания ног мы будем поднимать только одну ногу (в данном случае поднимается права нога).
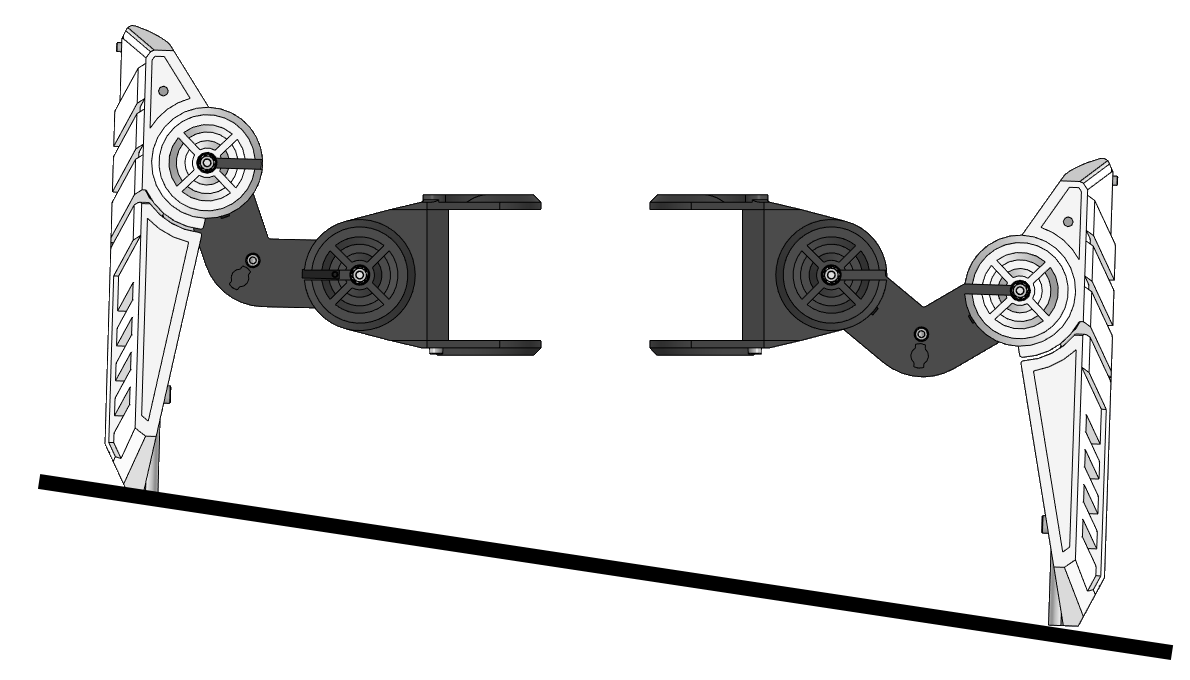
Такой подход немного усложняет расчеты, т.к. плоскость должна проходить не через (0;0;0), а через точку касания самой удаленной от центра гексапода конечности, причем с противоположной стороны наклона. Т.е. мы переносим начало координат в точку касания левой ноги. С виду сложности нет пока мы работаем по одной оси и с двумя конечностями.
Веселье начинается когда, появляется наклон по второй оси и еще 4 конечности, которые расположены далеко не на одной прямой, так они еще и постоянно меняют координаты точек касания во время походки. Веселье в том, что необходимо каждый раз пробегаться по координатам ног и выявлять самую удаленную, и уже относительно неё формировать уравнение плоскости. В целом это несложно, но всё же нюанс.
Реализация
Взглянем на код всего этого счастья. В данном коде для упрощения понимания я убрал обход конечностей и получения их координат, заменив их константами. По сути мы рассматриваем стабилизацию, когда гексапод не двигается.
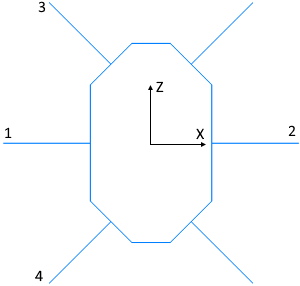
-135.0f + 80.0f определяют точку "1";
135.0f + 80.0f определяют точку "2";
70.0f + 104.0f определяют точку "3";
-70.0f + 104.0f определяют точку "4";
// Surface normal
point_3d_t n;
n.x = 0;
n.y = 1;
n.z = 0;
// Move surface to max position
point_3d_t a = {0, 0, 0};
if (z_rotate < 0) a.x = +(135.0f + 80.0f);
else a.x = -(135.0f + 80.f);
if (x_rotate < 0) a.z = +(70.0f + 104.0f);
else a.z = -(70.0f + 104.0f);
// Rotate normal by axis X
float x_rotate_rad = DEG_TO_RAD(x_rotate);
n.x = n.x;
n.y = n.y * cosf(x_rotate_rad) + n.z * sinf(x_rotate_rad);
n.z = n.y * sinf(x_rotate_rad) - n.z * cosf(x_rotate_rad);
// Rotate normal by axis Z
float z_rotate_rad = DEG_TO_RAD(z_rotate);
n.x = n.x * cosf(z_rotate_rad) + n.y * sinf(z_rotate_rad);
n.y = n.x * sinf(z_rotate_rad) - n.y * cosf(z_rotate_rad);
n.z = n.z;
// Calculate Y offsets
for (int32_t i = 0; i < sizeof(g_limbs) / sizeof(g_limbs[0]); ++i) {
float z_sign = 1.0f;
if (g_limbs[i].position.z != 0) {
z_sign = g_limbs[i].position.z / fabs(g_limbs[i].position.z);
}
float z = g_limbs[i].position.z + z_sign * 104.0f; // 104 - coxa position from center by axix Z
float x_sign = 1.0f;
if (g_limbs[i].position.x != 0) {
x_sign = g_limbs[i].position.x / fabs(g_limbs[i].position.x);
}
float x = g_limbs[i].position.x + x_sign * 104.0f;
offsets[i] = (-1) * (-n.z * (z - a.z) - n.x * (x - a.x)) / n.y;
}В начале мы определяем нормаль и поворачиваем её по осям X и Z на углы, которые мы получили из MPU6050. На основании знака угла наклона мы можем определить в какую сторону наклонено тело гексапода и сформировать нужную точку, через которую будет проходить плоскость. Зная вектор и точку мы можем построить уравнение плоскости:
Отсюда нам нужен Y
Но нам нужен не абсолютный Y, а смещение, т.е. на сколько нам нужно сдвинуть конечность, чтобы выровнять корпус. Поэтому y0 можно убрать, он будет добавлен при расчете кинематики.
Результат
Немного фото во время процесса переборки




Костыли
Ну куда же без них. В процессе работы с HX711 оказалось, что после считывания данных с них новая конверсия начинается на сразу, т.е. читать данные не обязательно, конверсия будет начинаться и без этого. Т.к. частота внутреннего тактового генератора в HX711 зависит от всего что только можно, разумеется получалась рассинхронизация и ни о какой параллельной работе с АЦП и речи быть не может.
Пришлось тактировать их от ноги STM32F030 и проводками припаиваться к ноге HX711, которая используется для подачи тактов от внешнего источника. Это позволило синхронизировать все АЦП и параллельно считывать с них данные. Но с этим нужно будет что-то делать, т.к. передавать такты по проводам с частотой 8МГц неправильно.
P.S.
В целом статья получилась не очень объемной и достаточно простой. Спасибо всем за внимание. Надеюсь я кого-нибудь смог убедить, что стабилизация шестиногих роботов дело достаточно простое и эту задачу можно решить обладая школьными знаниями :)