Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!

Всем привет! Разработка гексапода продвинулась на еще один шаг. На этот раз реализованы и протестированы траектории движения конечности — очередная часть математики передвижения. В этой статье я расскажу об этих траекториях и базовых последовательностях для движения. Надеюсь будет интересно.
Траектории
Суть данного механизма состоит в том, что при задании двух точек можно выбрать траекторию движения конечности. При движении из одной точки в другую координаты будут меняться по определенным параметрическим уравнениям. Механизм получился достаточно мощным и позволяет получать интересные кривые для движения. Так же при помощи него реализуется сглаживание движений за счет изменения шага параметра t — чем меньше шаг, тем больше будет промежуточных точек, соответственно ниже скорость и выше плавность движения.
Процедура задания параметров траектории местами немного непонятна и можно запутаться в ней. Сложность заключается в том, что при задании координат начальной и конечной точек не всегда задаются координаты реальных точек в пространстве, т.е. некоторые координаты задают параметры траектории. Пришлось написать программу, которая отображает заданную траекторию и заодно проверяет достижимость каждой точки траектории.
Драйвер поддерживает следующие траектории движения:
- XYZ_LINAR — самая простая из всех траекторий. Траектория используется при движении вперед, назад, подъеме и спуске. Все координаты меняются линейно и вычисляются следующим образом:
x = t * (x1 - x0) / 180.0f + x0; y = t * (y1 - y0) / 180.0f + y0; z = t * (z1 - z0) / 180.0f + z0;
Тут с понимаем проблем нет. Координаты задают углы параллелепипеда и они совпадают с реальными координатами. Движение происходит по диагонали параллелепипеда.
Визуализация траектории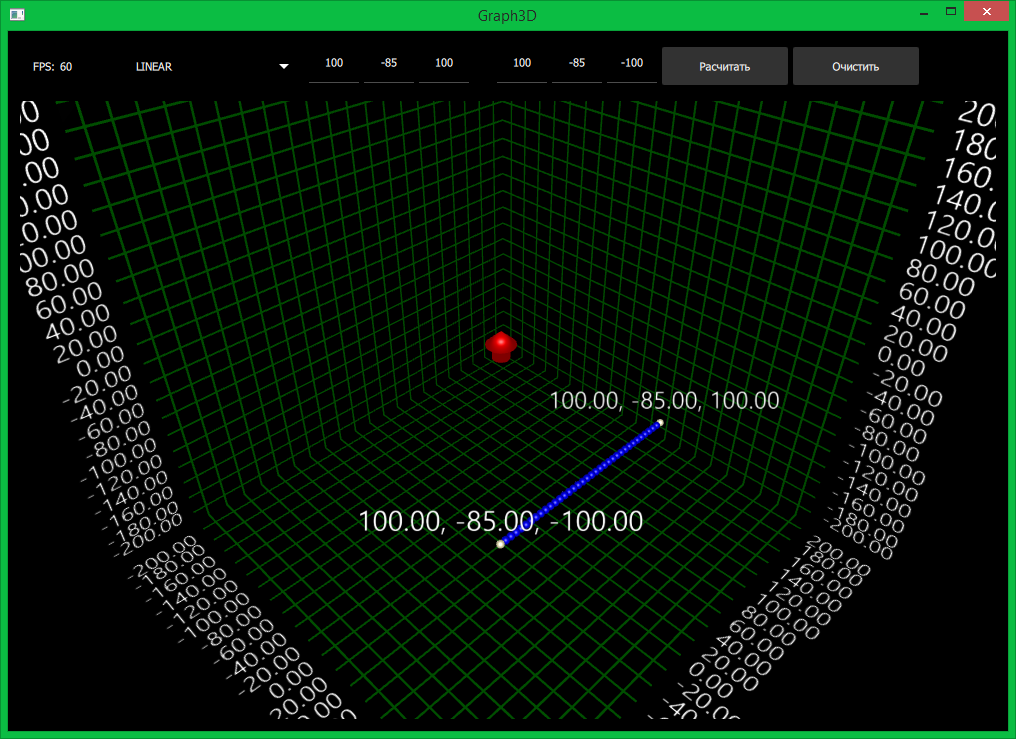

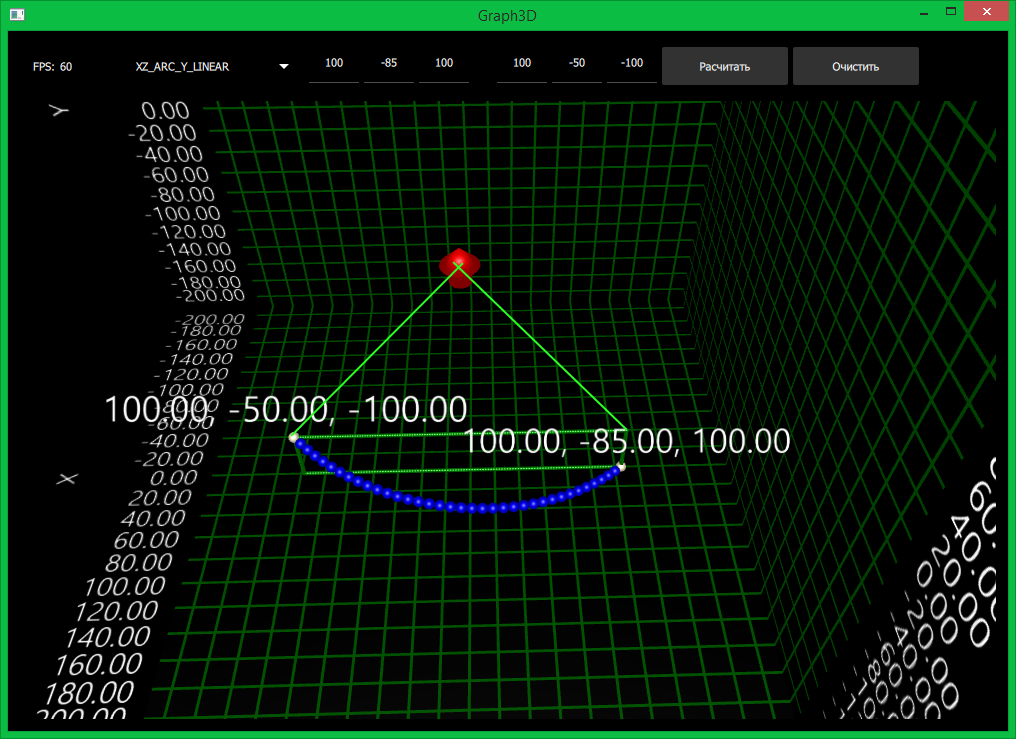
- YZ_ARC_Y_LINEAR — данная траектория позволяет реализовать движение по дуге. Траектория используется при повороте, когда нужно переместить конечность по земле. Координаты вычисляются следующим образом:
float R = sqrt(x0 * x0 + z0 * z0); float atan0 = RAD_TO_DEG(atan2(x0, z0)); float atan1 = RAD_TO_DEG(atan2(x1, z1)); float t_mapped_rad = DEG_TO_RAD(t * (atan1 - atan0) / 180.0f + atan0); x = R * sin(t_mapped_rad); // Circle Y y = t * (y1 - y0) / 180.0f + y0; z = R * cos(t_mapped_rad); // Circle X
Вот тут начинается веселье. Координаты задают направления лучей для ограничения дуги и они могут не совпадать с реальными координатами. Лучи находятся в одной плоскости, при этом радиус окружности равен длине вектора до начальной точки.
Визуализация траектории
- XZ_ARC_Y_SINUS — данная траектория так же позволяет реализовать движение по дуге, но более сложное, чем YZ_ARC_Y_LINEAR. Траектория используется при повороте, когда нужно переместить конечность по воздуху. Координаты вычисляются следующим образом:
float R = sqrt(x0 * x0 + z0 * z0); float atan0 = RAD_TO_DEG(atan2(x0, z0)); float atan1 = RAD_TO_DEG(atan2(x1, z1)); float t_mapped_rad = DEG_TO_RAD(t * (atan1 - atan0) / 180.0f + atan0); x = R * sin(t_mapped_rad); // circle Y y = (y1 - y0) * sin(DEG_TO_RAD(t)) + y0; z = R * cos(t_mapped_rad); // circle X
Веселье продолжается. Координаты так же задают направления лучей для ограничения дуги, но они НЕ совпадают с реальными координатами. Координата Y целевой точки задает высоту синуса.
Визуализация траектории
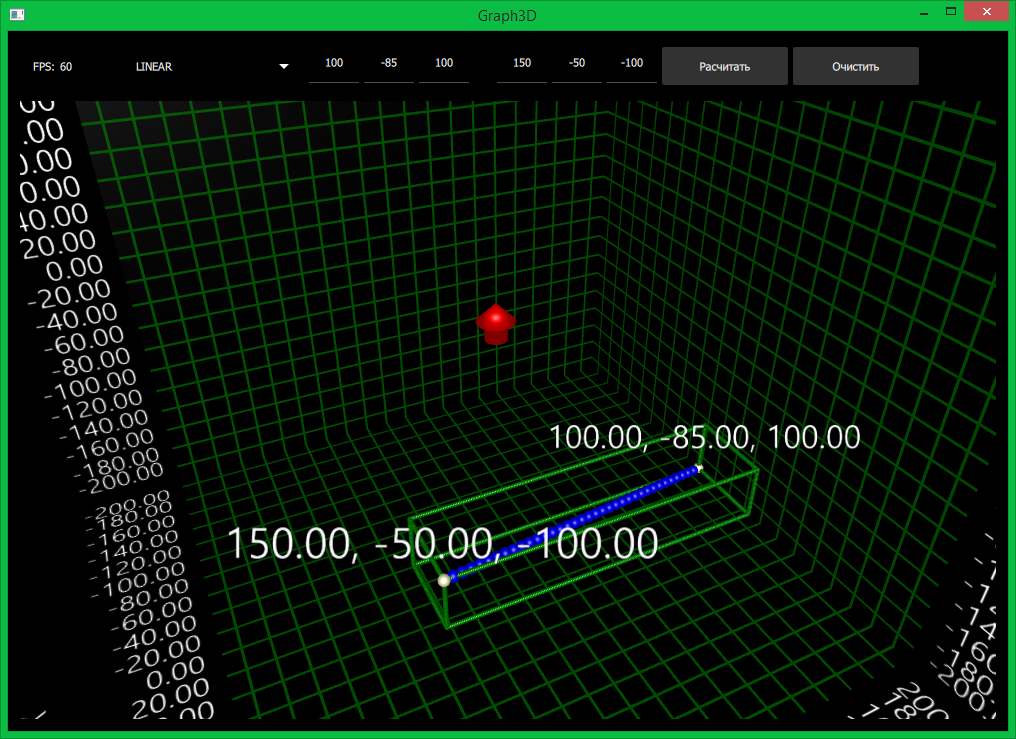
- XZ_ELLIPTICAL_Y_SINUS — данная траектория позволяет реализовать движение по эллипсу. Траектория используется при движении вперед и назад, когда нужно переместить конечность по воздуху. Данная траектория является усложнением XZ_ARC_Y_SINUS и понадобилась только из-за визуально некрасивой походки при использовании XZ_ARC_Y_SINUS (ноги слишком сильно выпирали). Координаты вычисляются следующим образом:
float a = (z1 - z0) / 2.0f; float b = (x1 - x0); float c = (y1 - y0); x = b * sin(DEG_TO_RAD(180.0f - t)) + x0; // circle Y y = c * sin(DEG_TO_RAD(t)) + y0; z = a * cos(DEG_TO_RAD(180.0f - t)) + z0 + a;
Координаты задают углы параллелепипеда и они НЕ совпадают с реальными координатами. Движение происходит из нижних углов параллелепипеда, находящихся в одной плоскости с касанием верней его части. Тут лучше посмотреть картинку в спойлере, я не знаю как это кратко описать словами.
Визуализация траектории
На этом базовая математика передвижения гексапода заканчивается. В моем проекте это необходимый минимум для реализации почти любых движений.
Последовательности
Немного теории
Последовательности — это элементарные действия из которых состоит походка. Делятся они на цикличные и не цикличные.
- Цикличные последовательности могут выполняться много раз и в конце каждого цикла должны возвращать конечности в исходное положение (движение и поворот);
- Не цикличные последовательности выполняются только один раз (подъем и спуск);
Каждая последовательность имеет три блока итераций: блок подготовки, основной блок, блок завершения.
- Блок подготовки — содержит итерации для перемещения конечностей в начальное положение для последовательности. В моем случае движение вперед требует выставление ног в определенное положение перед началом движения. Выполняется однократно при переходе к последовательности;
- Основной блок — содержит основные итерации последовательности. Может выполняться циклично;
- Блок завершения — содержит итерации для перемещения конечностей в базовое положение (положение, в которое устанавливаются конечности после подъема);
На рисунке ниже показана последовательность для движения вперед.
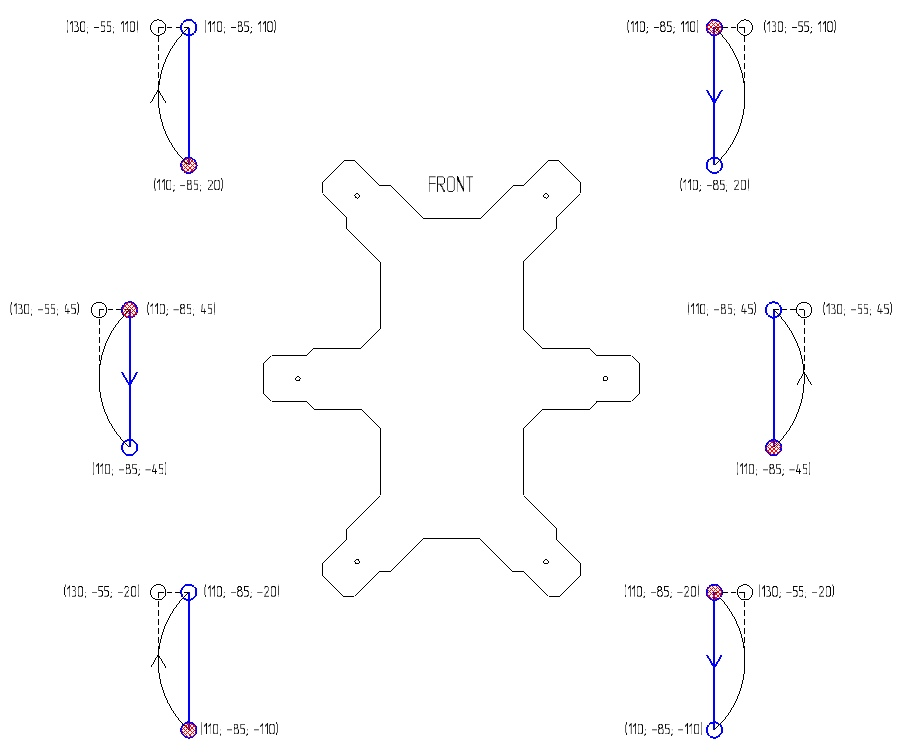
- Красными точками обозначены начальные положения конечностей перед началом движения
- Синими линиями обозначены траектории движения конечности по земле
- Черными линиями обозначены траектории движения конечности по воздуху
- Стрелками обозначен порядок выполнения последовательности
Координаты точек выбираются исходя из конфигурации корпуса. Я выбирал точки как можно ближе к корпусу для уменьшения длины рычага. За один цикл последовательности гексапод перемещается на 18см (за 1 цикл делается 2 шага — по 1 шагу на 3 конечности). Если сделать расстояние больше, то конечности начнут цеплять друг друга. Данный параметр ограничивается только конфигурацией корпуса.

Последовательность задается двумя точками (1, 2) для каждой конечности и используются две траектории: XYZ_LINEAR (синие линии) и XZ_ELLIPTICAL_Y_SINUS (черные линии). Точка 1 используется траекторией XZ_ELLIPTICAL_Y_SINUS для установки высоты синуса и соответственно высоты, на которую поднимется нога. Точка 2 и 3 являются реальными точками, которых достигает конечность при движении.
Расположение точек зависит только от вашей фантазии и возможностей гексапода. Возможно это все получилось немного сложно и есть более простой вариант, но видимо я пока до него не дошел.
Реализация
Теперь немного разберем реализацию всего этого счастья. Структуры с параметрами последовательности выглядит следующим образом:
typedef struct {
point_3d_t point_list[SUPPORT_LIMB_COUNT];
path_type_t path_list[SUPPORT_LIMB_COUNT];
uint32_t smooth_point_count;
} sequence_iteration_t;
typedef struct {
bool is_sequence_looped;
uint32_t main_sequence_begin;
uint32_t finalize_sequence_begin;
uint32_t total_iteration_count;
sequence_iteration_t iteration_list[15];
sequence_id_t available_sequences[SUPPORT_SEQUENCE_COUNT];
} sequence_info_t;sequence_iteration_t — содержит информацию об итерации последовательности:
- point_list — массив точек для каждой конечности в формате XYZ;
- path_list — массив траекторий для каждой конечности;
- smooth_point_count — задает количество точек траектории (шаг параметра t);
sequence_info_t — содержит информацию о всей последовательности:
- is_sequence_looped — задает тип последовательности: цикличная или нет;
- main_sequence_begin — задает начальный индекс основного блока в массиве iteration_list;
- finalize_sequence_begin — задает начальный индекс блока завершения в массиве iteration_list;
- total_iteration_count — задает количество итераций в последовательности;
- iteration_list — массив итераций;
- available_sequences — задает список последовательностей, доступных для перехода из текущей (допустим, мы не можем начать ходить, не встав сначала с пола);
NOTE: Индекс блока подготовки не указывается намеренно, он всегда располагается в начале массива итераций.
К сожалению, код определения последовательности представить тут не могу, т.к. он довольно широкий и после переносов ужасно выглядит. Я просто оставлю тут ссылку на файл с определениями.
Схема обработки движений
Стоит разобрать все круги ада, которые проходит последовательность во время выполнения. Схема обработки выглядит следующим образом:
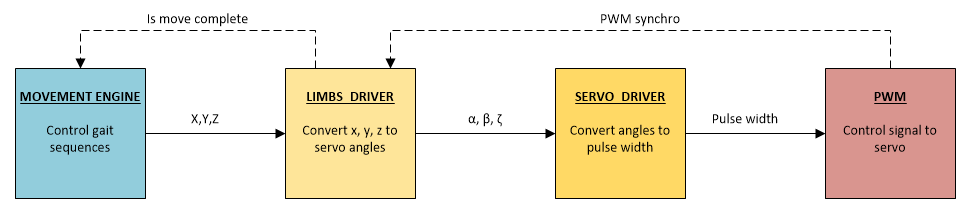
- MOVEMENT ENGINE — занимается организацией обработки и переключением между последовательностями. Никаких вычислений там не проводится. Если упрощенно, то этот модуль подсовывает следующую точку модулю «LIBMS DRIVER» после завершения обработки текущей.
Вход модуля: массив координат целевых точек.
Выход модуля: целевая точка для текущей итерации последовательности. - LIBMS DRIVER — самый сложный из всех модулей. Тут царит вся математика передвижения: обратная кинематика, расчеты траекторий и сглаживание движений. Этот модуль имеет строгую синхронизацию с модулем PWM. Расчеты проводятся c частотой 150Hz, соответственно управляющий импульс на приводы так же подается с частотой 150Hz.
Вход модуля: координаты целевой точки.
Выход модуля: углы поворота сервоприводов. - SERVO DRIVER. Нечего особенного в нем нет, кроме кучи параметров для настройки и корректировки приводов.
Вход модуля: углы поворота сервоприводов.
Выход модуля: ширина управляющего импульса. - PWM DRIVER. Драйвер программного ШИМ для управления приводами. Тут просто дергаются пины в нужные моменты времени. Переменная для синхронизации «PWM synchro» инкрементируется каждый период PWM.
Вход модуля: ширина управляющего импульса.
Выход модуля: импульсы на управляющих пинах.
Я попытался сделать модули независимыми друг от друга и у меня это получилось. Это позволяет вставить в эту схему любой промежуточный модуль (допустим модуль адаптации к ланшафту) и нечего при этом не сломается, при этом внедрение произойдет с минимальными изменениями в коде.
Последние новости и найденные раки проекта
Последние новости
- Вышел нового тестовый вариант корпуса (архив с чертежами) и я его немного покрасил. Полная сборка гексапода с выставлением насадок приводов в центральное положение занимает 7 — 8 часов непрерывной сборки и это если учитывать, что я уже не однократно проводил эту процедуру.
Фотки



- Поставил на него OLED дисплей для вывода какой-нибудь инфы, получилось довольно красиво.
Фотки

- Запущена коммуникация через WIFI. Теперь он управляется с телефона (тулзу пришлось написать свою)
- Снижено напряжение питания с 12V до 7V из-за проблем с перегревом платы питания
- К выходу 5 части разработки выложу ссылку на исходники, они наконец-то приобрели состояние при котором их не стыдно показать людям
Найденные раки
Кстати калибровку делал при помощи этого устройства:

- HC-SR04. Я знал, что этот датчик плохой, но не думал что настолько. В общем, нужен другой дальнометр
- MG996R не соответствуют заявленным характеристикам. Обещали 12кг\см — по факту 5кг\см при PWM с частотой 300Гц, при 50Гц еще хуже и к тому же они оказались аналоговыми (обещали цифру). Годятся только для поворотов. Пришлось перейти на более дорогие цифровые приводы DS3218 на 20кг\см — по факту 23кг\см
- Составил таблицу «угол-импульс» через каждые 10 градусов и заметил, что значения ширины управляющего импульса для MG996R находятся на разном расстоянии друг от друга. Пришлось делать калибровочные таблицы для каждого привода и вычислять импульс индивидуально.
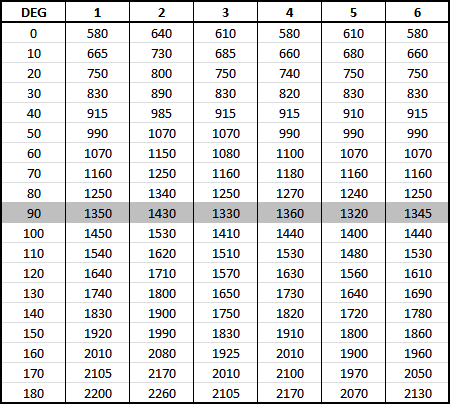
Как видно, шаг импульса для каждого привода отличаются, это было неожиданным для меня открытием. - Минимальное, максимальное и центральное значения импульса отличаются из-за насадок для приводов (как их ни крути, все равно не ровно). На рисунке показаны приводы, на которые подается импульс 1500us и видно, что одна насадка находится не по центру и соответственно приходится подгонять импульс так, чтобы все насадки находились в одном и том же положении.

Кстати калибровку делал при помощи этого устройства: