Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В конце прошлого года, Booking.com запустил соревнование по построению рекомендательного алгорима для путешественников. Задача — наилучшим образом предсказать следующий город для пользователя, основывываясь на предыдущих посещенных городах.

Рекомендации городов в booking.com, картинка отсюда
В этой статье мы опишем наше решение задачи, которое заняло 5е место на соревновании. Наше решение основано на нейросетевом механизме внимания, а так же на основе listwise-метода обучения ранжированию LambdaRank. Наше решение выбирает правильный город в четыре рекомендованных города с вероятностью 55.5%, что есть довольно неплохой результат, учитывая что алгоритму необходимо было выбирать 4 города из практически 40000 возможных.
Эта статья — расширенная версия нашей статьи, которая была принята и опубликована на воркшопе по web-туризму в рамках конференции WSDM.
Мы предполагаем что читатель уже немного знаком с основными понятиями из области обучения нейросетей, и поэтому будем фокусироваться именно на нашем решении.
Описание задачи
Задача, предложенная на соревновании, состояла в том, чтобы разработать рекомендательный алгоритм, который рекомендовал бы следующий город пользователю на основании уже посещенных им городов. Для разработки рекомендательного алгоритма, организаторы предложили датасет состоящий из двух частей train и test. Каждая строчка датасета содержит следующие данные:
| Колонка | Описание |
|---|---|
| user_id | Id пользователя |
| checkin | Дата въезда в отель |
| checkout | Дата выезда из отеля |
| affiliate_id | Анонимизированный Id источника трафика (Например поисковая система) |
| device_class | Desktop/Mobile |
| booker_country | Страна из которой было выполнено бронирование |
| hotel_country | Страна отеля (анонимизированно) |
| city_id | Город отеля (анонимизированно) |
| utrip_id | Идентификатор путешествия |
| user_id | checkin | checkout | city_id | device_class | affiliate_id | booker_country | hotel_country | utrip_id | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1006220 | 2016-04-09 | 2016-04-11 | 31114 | desktop | 384 | Gondal | Gondal | 1006220_1 |
| 1 | 1006220 | 2016-04-11 | 2016-04-12 | 39641 | desktop | 384 | Gondal | Gondal | 1006220_1 |
| 2 | 1006220 | 2016-04-12 | 2016-04-16 | 20232 | desktop | 384 | Gondal | Glubbdubdrib | 1006220_1 |
| 3 | 1006220 | 2016-04-16 | 2016-04-17 | 24144 | desktop | 384 | Gondal | Gondal | 1006220_1 |
| 4 | 1010293 | 2016-07-09 | 2016-07-10 | 5325 | mobile | 359 | The Devilfire Empire | Cobra Island | 1010293_1 |
| 5 | 1010293 | 2016-07-10 | 2016-07-11 | 55 | mobile | 359 | The Devilfire Empire | Cobra Island | 1010293_1 |
| 6 | 1010293 | 2016-07-12 | 2016-07-13 | 23921 | mobile | 359 | The Devilfire Empire | Cobra Island | 1010293_1 |
| 7 | 1010293 | 2016-07-13 | 2016-07-15 | 65322 | desktop | 9924 | The Devilfire Empire | Cobra Island | 1010293_1 |
| 8 | 1010293 | 2016-07-15 | 2016-07-16 | 23921 | desktop | 9924 | The Devilfire Empire | Cobra Island | 1010293_1 |
| 9 | 1010293 | 2016-07-16 | 2016-07-17 | 20545 | desktop | 10573 | The Devilfire Empire | Cobra Island | 1010293_1 |
В тестовой части датасета, последний город в путешествии и страна последнего города были замаскированы; остальные параметры, например дата въезда и дата выезда, доступны. Задача участников соревнования — для каждого путешествия из тестовой части датасета порекомендовать 4 варианта последнего города. Участники оценивались по метрике Accuracy@4. По сути, эта метрика показыват сколько процентов рекомендаций содержали правильный город.
Переранжирующая модель на основе механизма внимания.
Метрика Accuracy@4 по своей сути является метрикой ранжирования: мы можем сгенерировать скор для всех возможных городов, отсортировать их и оценить вероятность с которой целевой город окажется среди топ-4х городов. Так как наша целевая метрика является метрикой ранжирования, мы решали задачу как задачу ранжирования.
Сама по себе метрика Accuracy@4 не очень удобна для оптимизации напрямую, тал как она учитывает выставленный скор только для четырех городов и никак не учитывает взаимный порядок между этими четыремя городами. Для того, чтобы облегчить себе задачу, мы заменили эту метрику другой популярной метрикой ранжирования, а именно метрикой NDCG@40.
Метрика NDCG расшифровывается как Normalized Discounted Cumulative Gain. Эта метрика подходит для оценки порядка внтури списка документов; в нашем случае один документ это один рекомендуемый город.
Для того, чтобы посчитать NDCG нам сначала надо посчить другую метрику, Dicounted Cumulative Gain (DCG).
Пусть у нас есть список из K документов, и мы знаем, что релевантность i-го документа равна ri
Тогда, метрика DCG@K считается по формуле:
Теперь мы можем определить NDCG:
где IDCG (Ideal DCG)- это DCG для того же списка документов, переупорядоченных в соответствии с релевантностью документов.
Метрика NDCG в идеальном случае всегда равна единице. Ее значение зависит только от порядка документов.
Так как метрика NDCG@K зависит не только от элементов, включенных в список рекомендаций, но и от их относительного порядка, ее значение более стабильно по сравнению с метрикой Accuracy@K. Кроме того, мы увеличили стабильность метрики за счет того, что выбрали большее значение K (40 вместо 4).
Еще одной проблемой метрик ранжирования, таких как NDCG@K или Accuracy@K, является тот факт, что их значение изменяется скачкообразно при изменении порядка элементов в списке рекомендаций. Это означает, что такие метрики не являются гладкими и дифференцируемыми и их нельзя напрямую оптимизировать классическим методом градиентного спуска.
Градиентный спуск и его вариации служат основой для оптимизации нейросетевых алгоритмов. Так как он не работает напрямую с метриками ранжирования, на практике при решении задачи ранжирования часто оптимизируют прокси-метрики, такие как log loss, в надежде, что их оптимизация приведет к улучшению качества ранжирования. Нам не очень понравилась такая идея, и мы решили все-таки попытаться оптимизировать саму метрику NDCG напрямую.
Для прямой оптимизации метрики NDCG существует метод LambdaMART[1]. Это метод, работающий на основе градиентного бустинга над деревьями принятия решений. Например, он реализован в популярных библиотеках LightGBM и XGboost и является рабочей лошадкой для решения задач ранжирования. Например, этот метод работает в Bing для ранжирования поисковых результатов, применяют в Amazon, да и Яндексовый YetiRank является близким родственником данного подхода.
В основе метода лежит идея замены градиента лосс-функции специально сконструированными значениями, называемыми лямбда-градиент, используя которые в методе градиентного спуска можно оптимизировать метрику NDCG. Мы реализовали этот метод для обучения нейросетей и применили для решения нашей задачи. В итоге, верхнеуровнево, наше решение выглядит следующим образом:
- Выбрать города-кандидаты для рекомендаций при помощи простых эвристических алгоритмов.
- Сгенерировать матрицу C фичей для кандидатов.
- Сгенерировать векторные представления T предыдущих городов в текущей поездке при помощи Transformer-like архитектуры.
- Сгенерировать векторное представление F целевого города на основе доступных фичей. Несмотря на то что мы не знаем идентификатор города, мы можем использовать такие параметры как дата въезда и выезда, тип устройства и т.д.
- Сгенерировать скор для кандидатов и отсортировать их в соответствии с этим скором. Для этого, мы применяем механизм внимания между кандидатами и посещенными городами. Результат этой операции скалярно умножаем на векторное представление фичей и получаем результат.
Теперь разберем нашу модель подробнее.
Генерация лейблов
Для обучения нейросетевой модели нам нужны размеченные примеры, для которых мы уже знаем правильный ответ. Для этого, мы применили следующую процедуру:
1) Сортируем города из путешествия по времени
2) Несколько последних городов в путешествии объявляем "целевыми". Конкретное количество целевых городов определяем случайным образом для каждого путешествия
3) Назначаем для i-го города в целевой части скор 2-i. Идея назначать экспоненциально уменьшающийся вес базируется на том, что чем на более далекое будущее приходится посещение города, тем меньше влияние предыдущих городов и тем больше влияние других факторов, которые наша модель не может учесть.
Отбор кандидатов для ранжирования
Наша подход основан на методе оптимизации LambdaRANK.
Этот подход требует довольно тяжелых вычислений, и поэтому мы можем его применять только на ограниченном количестве кандидатов. Поэтому, нам необходимо было отобрать города-кандидаты используя более простой подход. Для того, чтобы тренировать нашу модель за разумное время мы решили ограничиться 500 городами-кандидатами для каждого путешествия из 39870 возможных. Мы использовали смесь простых моделей для того, чтобы выбрать эти 500 кандидатов.
В течении каждой из эпох на этапе обучения, мы выбирали 10000 путешествий для обучения нашей основной нейросети, а оставшиеся путешествия из датасета использовали для обучения простых моделей, использованных для отбора кандидатов. Такое разделение необходимо, так как результаты работы простых моделей мы подавали на вход нейросети в качестве входных данных. Без разделения данных на две части наша нейросеть бы переобучилась.
Вот список простых моделей и правил, которые мы использовали для генерации 500 кандидатов:
1. Все предыдущие посещенные города из путешествия
Мы обратили внимание на то, что в датасете довольно часто внутри одного путешествия несколько раз встречается один и тот же город. Это можно объяснить тем, что люди приезжают в "базовый" город и из этого базового города посещают несколько соседних городов.
2. Transition chain
Данная модель использует последовательную природу посещений городов в модели.
Предположим, что в нашем датасете всего $M$ городов, и каждое путешествие представляет из себя последовательность из $K$ городов, где $K$-й город в последовательности — это наш целевой город. Мы можем создать матрицу переходов в последний город $T \in R^{M \times M}$, которую мы заполним, используя следующую процедуру:
procedure fillTransitionMatrix
T ← zero matrix with size M × M
for current_trip in trips do:
last_city ← current_trip [−1]
prev_cities ← current_trip [: −1]
for city in prev_cities do:
T [city][last_city] += 1.
end for
end for
end procedureПроцедура генерации кандидатов используя данную матрицу очень простая: мы суммируем строчки нашей матрицы для всех городов из путешествия. В результате, затем выбираем в качестве кандидатов города, суммарный результат для которых получился максимальный.
Используя данную процедуру, мы добавляли города в множество кандидатов, до тех пор пока размер множества кандидатов не достиг 150 или не закончились города с ненулевым скором.
3. BookerTripCountryTop
Данный метод представляет из себя простую эвристику. Мы отбираем самые популярные города для путешествий, среди пользователей из страны, совпадающей со страной текущего пользователя, которые путешествовали в страну, которая совпадает со страной последнего города из текущего путешествия.
Используя данную эвристику мы добавляли города в множество кандидатов, до тех пор, пока его размер не достиг 350.
4. LastCityCountryTop
Используя эту эвристику мы отбирали самые популярные города в стране последнего города текущего путешествия. Данная эвристика похожа на предыдущую, но мы считаем топ без учета страны пользователя.
Используя данную эвристику мы добавляли города в множество кандидатов, до тех пор, пока его размер не достиг 500.
Используя эвристики описанные выше, мы зачастую могли полностью заполнить множество кандидатов. Однако, в некоторых ситуациях, нам не хватало городов. Например, такое могло случится, когда пользователь из редкой страны путешествует в другую редкую страну — в этом случае алгоритмы TransitionChain, BookerTripCountryTop и LastCityCountryTop могут сгенерировать лишь небольшое количество городов-кандидатов с ненулевым скором. В такой ситуации мы использовали два дополнительных метода отбора кандидатов, используя следующие эвристики:
5. BookerCountryTop — Самые популярные города среди путешественников из страны, совпадающей со страной текущего пользователя.
6. GlobalTop — Самые популярные города в датасете.
Используя описанные шесть эвристик мы могли гарантированно заполнить массив из 500 городов-кандидатов. Наши эксперименты показали, что используя данные эвристики, вероятность включения нужного города в список кандидатов (метрика recall@500) составляет примерно 90%.
Генерируем фичи для кандидатов.
Для того, чтобы облегчить жизнь нашей нейросети, для каждого города-кандидата мы сгенерировали набор фичей. Теоретически, если бы количество тренировочных данных в датасете было неограниченно, мы бы могли избежать генерации фичей вручную и положиться доверить нейросети выучить эмбеддинги. Однако, поскольку датасет был ограничен в размере, то добавление данных фичей улучшило результат работы нашей модели.
Мы для каждого города-кандидата мы генерировали векторное представление, используя следующие фичи:
- Популярность города-кандидата среди всех пользователей и среди пользователей из данной страны
- Популярность города-кандидата по месяцам и годам (чтобы учесть сезонность)
- Скоры из простых рекомендательных моделей, использованных для отбора кандидатов
- Бинарный флаг — совпадает ли город-кандидат с первым городом в путешествии
- Бинарный флаг для каждого из пяти последних городов в путешествии — совпадает ли наш город-кандидат с этим последним городом
- Косинусная близость города-кандидата к каждому из последних пяти городов в путешествии, посчитанная на основе одновременных посещений городов в тренировочных данных
- Дополнительно к вручную сгенерированным фичам кандидатов, мы добавляли обучаемый эмбеддинг города.
Генерируем векторе представление путешествия
Наша модель использует нейросетевую архитектуру, похожую на архитектуру Transformer[2] для того, чтобы закодироияя. Архитектура Transformer хорошо подходит для обработки текстов. Использование данной архитектуры базируется на том факте, что последовательность городов в путешествии похожа на последовательность слов в тексте.
Мы сгенерировали векторное представление каждого города в путешествии используя следующие признаки:
- Эмбеддинг города, 32 обучаемых параметра.
- Эмбеддинг страны пользователя, 32 обучаемых параметра.
- Эмбеддинг страны города — 32 обучаемых параметра. Данный эмбеддинг использует те же веса, что и эмбеддинг страны пользователя.
- Эмбеддинг источника траффика(affiliate id) — 5 обучаемых параметров
- Некоторое количество фичей, разработанных нами вручную, включая:
— Количество ночей между въездом и выездом в отель.
— Захватывает ли остановка в отеле выходные? (хороший признак для того, чтобы отличать командировки)
— Совпадает ли страна города с предыдущими со страной предыдущих городов в путешествии.
— День недели и неделя в году для даты въезда и выезда.
— Совпадает ли страна пользователя и страна города?
— Год въезда. 3 параметра, one-hot encoded. В датасете представлены путешествия только за 3 года.
— Месяц въезда. 12 параметров, one-hot encoded.
Всего, каждый город в путешествии был представлен смесью из 115 обучаемых и фиксированных параметров.
Для того, чтобы получить более качественное семантическое представление городов в путешествии, мы закодировали их используя один полносвязный слой нейросети размерности 115. Для того, чтобы учесть позицию города в путешествии, мы так же умножили этот вектор на эмбеддинг позиции. В оригинальной архитектуре Transformer, авторы используют фиксированные эмбеддинги, основанные на функциях $sin$ и $cos$ Вместо этого, мы использовали два обучаемых эмбеддинга, представляющих собой позицию города относительно начала и конца путешествия. Мы сконкатенировали эти эмбеддинги и пропустили их через один полносвязный слой для того, чтобы получить финальный эмбеддинг города в путешествии.
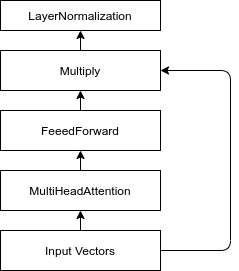
Transformer-like блок. По сравнению с оригинальным блоком transformer, мы заменили сложение на умножение в residual-связи
Для того, чтобы смоделировать взаимодействия городов друг с другом, мы воспользовались архитектурой Transformer. Оригинальный блок архитектуры Transformer состоит из одного Self-Attention слоя, Dense-слоя, Residual-связи и нормализации. На хабре уже неоднократно разбирали архитектуру Transformer, поэтому мы не будем описывать ее тут. Единственная разница нашего transformer-like блока с оригинальным, заключается в том, что для residual связи мы используем не сложение, а умножение. Наши эксперименты показали, что на данном датасете, умножение позволяет обучиться быстрее и позволяет достичь более высокого результата.
На выходе из Transformer-like части нашей нейросети, мы получили представления городов обогащенные информацией о других городах из того же путешествия. Затем, мы моделировали взаимодействия этих представлений с нашими городами-кандидатами. Для этого мы использовали следующие шаги:
- Закодировали матрицу городов-кандидатов, используя один полносвязный слой нейросети.
- Полученные представления городов-кандидатов мы пропустили через один Transformer-like блок. Интуитивно — города кандидаты не являются независимыми и, зная какие есть другие кандидаты, нейросети будет легче подобрать правильный скор для текущего города.
- При помощи одного слоя MultiHeadAttention смоделировали взаимодействия с предыдущими городами из путешествия. На выходе мы получили эмбеддинги городов-кандидатов в контексте текущего путешествия.
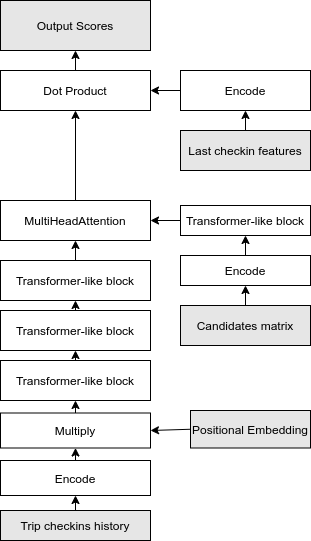
Архитектура нашей нейросети.
Финальный скор для каждого города-кандидата мы генерировали при помощи умножения (dot product) эмбеддинга города-кандидата на закодированное представление фичей последнего города. По условиям задачи, нам не известен последний город, но известные некоторые характеристики поездки в этот город, например время въезда и выезда и источник трафика. Мы закодировали эти параметры, используя те же самые процедуры, которые мы использовали для кодирования фичей городов в путешествии. Дополнительно, мы пропустили эти фичи через один полносзвязный слой нейросети, для того чтобы получить проекцию в то же пространство, в которое мы спроектировали эмбеддинги городов-кандидатов.
Обучаем модель
Как мы уже и писали выше, мы использоавали подход LambdaRANK, для того чтобы оптимизировать метрику NDCG напрямую.
Мы взяли имплементацию метода из библиотеки lightgbm в качестве референсной и написали собственную имплементацию, которая подходит для обучения нейросетей. Как показали наши эксперименты, использование метода LambdaRANK позволило нам намного быстрее обучать нашу нейросеть ранжировать города, по сравнению с использованием бинароной кроссэнтропией. Кроме того, метрика NDCG, которую оптимизирует LambdaRANK показала практически идеальную корелляцию с метрикой Accuracy@4, поэтому в целом обучая модель получать хороший скор NDCG, мы автоматом получали хорошее значение Accuracy@4.
Для тренировки мы использовали оптимизатор Adam с ранней остановкой после 50 эпох без улучшения метрики Accuracy@40
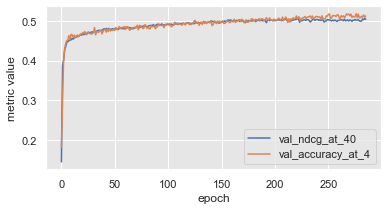
Метрики Accuracy@4 и NDCG@40. Видно что метрики кореллируют практически идеально. Такой выскоий уровень корреляции подсказывает что оптимизируя одну метрику, мы автоматом оптимизируем и другую
Для имплементации нашей нейросети мы использовали библиотеки Tensorflow и Keras. Тренировка заняла примерно 7 часов на GPU Nvidia RTX 3090.
Оценка качества модели и результаты
Схема валидации нашей модели была основана на отдельных путешествиях. Так как с нашей точки зрения большой разницы между частями train и test датасета не было, мы объединили эти части и использовали обе из них как для тренировки модели, так и для оценки качества. Мы случайным образом отобрали 4000 путешествий в тестовое множество (наше тестовое, не путать с частью test датасета) и еще 4000 в валидационное. Остальные путешествия из обоих датасетов мы поместили в тренировочную выборку. На этапе валидации и тестирования модели мы использовали все города кроме последнего для того, чтобы предсказать один последний город в каждом путешествии (стратегия leave one out).
Метрики
Для оценки качества нашей модели мы использовали следующие метрики:
- Accuracy@4 — Метрика использованная организаторами соревнования для оценки моделей.
- NDCG@40 — Метрика которую мы использовали в для оптимизации нашей нейросети. Как мы показали выше, данная метрика хорошо кореллирует с метрикой Accuracy@4.
- Leaderboard — По сути, это та же самая метрика Accuracy@4, измеренная организаторами соревнования на закрытой части датасета. По условиям соревнования, мы могли померять эту метрику лишь дважды: один раз для "предварительной" модели, и один раз для финальной модели.
Сравнение метрик с простыми моделями:
Для оценки качества нашей модели мы использовали следующие бейзлайны:
- GlobalTop, LastCityCountryTop, TransitionChain — простые эвристические алгоритмы которые мы использовали для отбора кандидатов.
- TruncatedSVD — Популярный подход для решения задачи построения рекомендательных систем на основе матричного разложения. Мы использовали реализацию TruncatedSVD из библиотеки sklearn.
- SelfAttention — end-to-end версия нашей модели. Архитектура данной модели похожа на нашу финальную модель. Отличие в том, что мы рассчитываем скор для всех городов, а не для топ-500 кандидатов. Из-за этого модель была более тяжеловесной, и мы не могли использовать фичи, которые мы генерировали вручную (например похожесть на предыдущие города из путешествия). По сути, при помощи Transformer-like части нашей модели мы генерировали эмбеддинг путешествия, и сравнивали с выученными эмбеддингами городов. Эту модель мы использовали для промежуточной оценки результата.
- LambdaMART Так как мы использовали подход LambdaRANK, мы хотели попробовать сравнить нашу имплементацию с классической реализацией данного подхода на деревьях принятия решений. Мы использовали имплементацию LambdaRANK из библиотеки lightgbm. Подход базировался тольк о на вручную сгенерированных фичах (описанных в секции "генерируем фичи для кандидатов" выше).
Результаты сравнения моделей представлены в следующей таблице:
| Модель | Accuracy@4 | NDCG@40 | Leaderboard |
|---|---|---|---|
| GlobalTop | 0.058 | 0.091 | - |
| TransitionChain | 0.440 | 0.429 | - |
| SelfAttention | 0.509 | 0.491 | 0.514 |
| LambdaMART | 0.514 | 0.485 | - |
| RerankingAttention | 0.542 | 0.513 | 0.555 |
Заключение
Участие в конкурсе от booking.com показало, что комбинация listwise методов ранжирования и современных нейросетевых архитектур, которая позволила нам набрать высокий скор в соревновании. Тот же самый подход может быть использован вместе с другими архитектурами нейросетей для решения большого количества задач на ранжирование из области информационного поиска, включая рекомендательные и поисковые системы.
Ссылки:
[1] Burges CJ. From ranknet to lambdarank to lambdamart: An overview
[2] Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser L, Polosukhin I. Attention is all you need. arXiv preprint arXiv:1706.03762. 2017 Jun 12.
(https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.180.634&rep=rep1&type=pdf). Learning. 2010 Jun 23;11(23-581):81.





