Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Мы это сделали!
 Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2588 в закладки, 429k прочтений)?
Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2588 в закладки, 429k прочтений)?
Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
За перевод спасибо Андрею Пахомову.
Теория Информации была разработана К. Э. Шенноном в конце 1940х годов. Руководство Лабораторий Белла настаивало, чтобы он назвал ее «Теория Связи», т.к. это намного более точное название. По очевидным причинам, название «Теория Информации» обладает значительно большим воздействием на публику, поэтому Шеннон выбрал именно его, и именно оно известно нам по сей день. Само название предполагает, что теория имеет дело с информацией, это и делает ее важной, поскольку мы все глубже проникаем в информационную эпоху. В этой главе я затрону несколько основных выводов из этой теории, приведу не строгие, а скорее интуитивно понятные доказательства некоторых отдельных положений этой теории, чтобы вы поняли, чем на самом деле является «Теория Информации», где вы можете ее применять, а где нет.
Прежде всего, что такое “информация”? Шеннон отождествляет информацию с неопределенностью. Он выбрал отрицательный логарифм вероятности события в качестве количественной меры информации, которую вы получаете при наступлении события с вероятностью p. Например, если я скажу вам, что в Лос-Анжелесе туманная погода, тогда р близок к 1, что по большому счету, не дает нам много информации. Но если я скажу, что в июне в Монтерей идет дождь, то в этом сообщении будет присутствовать неопределенность, и оно будет содержать в себе больше информации. Достоверное событие не содержит в себе никакой информации, поскольку log 1 = 0.
Остановимся на этом подробнее. Шеннон полагал, что количественная мера информации должна быть непрерывной функцией от вероятности события p, а для независимых событий она должна быть аддитивной – количество информации, полученное в результате осуществления двух независимых событий, должно равняться количеству информации, полученному в результате осуществления совместного события. Например, результат броска игральных костей и монеты обычно рассматриваются как независимые события. Переведем вышесказанное на язык математики. Если I (p) – это количество информации, которое содержится в событии с вероятностью p, то, для совместного события, состоящего из двух независимых событий x с вероятностью p1 и y с вероятностью p2 получаем

(x и y независимые события)
Это функциональное уравнение Коши, истинное для всех p1 и p2. Для решения этого функционального уравнения предположим, что
p1 = p2 = p,
это дает

Если p1 = p2 и p2 = p, тогда

и т.д. Расширяя этот процесс, используя стандартный метод для экспонент, для всех рациональных чисел m / n, верно следующее
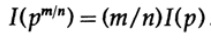
Из предполагаемой непрерывности информационной меры, следует, что логарифмическая функция является единственным непрерывным решением функционального уравнения Коши.
В теории информации принято принимать основание логарифма равное 2, поэтому бинарный выбор содержит ровно 1 бит информации. Следовательно, информация измеряется по формуле

Давайте приостановимся и разберемся, что же произошло выше. Прежде всего, мы так и не дали определение понятию “информация”, мы просто определили формулу ее количественной меры.
Во-вторых, эта мера зависит от неопределенности, и, хотя она в достаточной степени подходит для машин — например, телефонных системы, радио, телевидения, компьютеров и т. д. — она не отражает нормального человеческого отношения к информации.
В-третьих, это относительная мера, она зависит от текущего состояния вашего знания. Если вы смотрите на поток “случайных чисел” из генератора случайных чисел, вы предполагаете, что каждое следующее число неопределенно, но, если вы знаете формулу для вычисления «случайных чисел», следующее число будет известно, и, соответственно, не будет содержать в себе информации.
Таким образом, определение, данное Шенноном для информации, во многих случаях подходит для машин, но, похоже, не соответствует человеческому пониманию этого слова. Именно по этой причине «Теорию информации» следовало назвать «Теорией связи». Тем не менее, уже слишком поздно чтобы менять определения (благодаря которым теория приобрела свою первоначальную популярность, и которые все еще заставляют людей думать, что эта теория имеет дело с «информацией»), поэтому мы вынуждены с ними смириться, но при этом вы должны чётко понимать, насколько определение информации, данное Шенноном, далеко от своего общеупотребительного смысла. Информация Шеннона имеет дело с чем-то совершенно другим, а именно с неопределенностью.
Вот о чем нужно подумать, когда вы предлагаете какую-либо терминологию. Насколько предложенное определение, например, определение информации данное Шенноном, согласуется с вашей первоначальной идеей и насколько оно отличается? Почти нет термина, который бы в точности отражал ваше ранее видение концепции, но в конечном итоге, именно используемая терминология отражает смысл концепции, поэтому формализация чего-то посредством чётких определений всегда вносит некоторый шум.
Рассмотрим систему, алфавит которой состоит из символов q с вероятностями pi. В этом случае среднее количество информации в системе (её ожидаемое значение) равно:
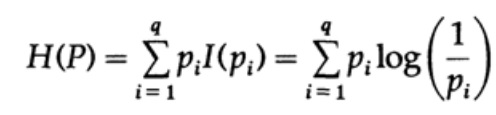
Это называется энтропией системы с распределением вероятности {pi}. Мы используем термин «энтропия», потому что та же самая математическая форма возникает в термодинамике и статистической механике. Именно поэтому термин «энтропия» создает вокруг себя некую ауру важности, которая, в конечном счете, не оправдана. Одинаковая математическая форма записи не подразумевает одинаковой интерпретации символов!
Энтропия распределения вероятности играет главную роль в теории кодирования. Неравенство Гиббса для двух разных распределений вероятности pi и qi является одним из важных следствий этой теории. Итак, мы должны доказать, что
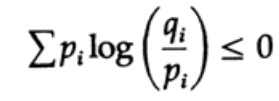
Доказательство опирается на очевидный график, рис. 13.I, который показывает, что
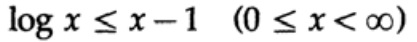
а равенство достигается только при x = 1. Применим неравенство к каждому слагаемому суммы из левой части:

Если алфавит системы связи состоит из q символов, то принимая вероятность передачи каждого символа qi = 1/q и подставляя q, получаем из неравенства Гиббса


Рисунок 13.I
Это говорит о том, что если вероятность передачи всех q символов одинакова и равна — 1 / q, то максимальная энтропия равна ln q, в противном случае выполняется неравенство.
В случае однозначно декодируемого кода, мы имеем неравенство Крафта
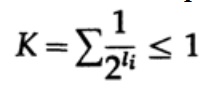
Теперь если мы определим псевдовероятности

где конечно = 1, что следует из неравенства Гиббса,
= 1, что следует из неравенства Гиббса,

и применим немного алгебры (помните, что K ≤ 1, поэтому мы можем опустить логарифмический член, и возможно, усилить неравенство позже), то получим

где L — это средняя длина кода.
Таким образом, энтропия является минимальной границей для любого посимвольного кода со средней длиной кодового слова L. Это теорема Шеннона для канала без помех.
Теперь рассмотрим главную теорему об ограничениях систем связи, в которых информация передаётся в виде потока независимых бит и присутствует шум. Подразумевается, что вероятность корректной передачи одного бита P > 1 / 2, а вероятность того, что значение бита будет инвертировано при передачи (произойдет ошибка) равняется Q = 1 — P. Для удобства предположим, что ошибки независимы и вероятность ошибки одинакова для каждого отправленного бита — то есть в канале связи присутствует «белый шум».
Путь мы имеем длинный поток из n бит, закодированные в одно сообщение — n — мерное расширение однобитового кода. Значение n мы определим позже. Рассмотрим сообщение, состоящее из n-битов как точку в n-мерном пространстве. Поскольку у нас есть n-мерное пространство — и для простоты будем предполагать, что каждое сообщение имеет одинаковую вероятность возникновения — существует M возможных сообщений (M также будет определено позже), следовательно, вероятность любого оправленного сообщения равняется
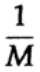

(отправитель)
График 13.II
Далее рассмотрим идею о пропускной способности канала. Не вдаваясь в подробности, пропускная способность канала определяется как максимальный объем информации, который может быть надежно передан по каналу связи, с учётом использования максимально эффективного кодирования. Нет доводов в пользу того, что через канал связи может быть передано больше информации, чем его емкость. Это можно доказать для бинарного симметричного канала (который мы используем в нашем случае). Емкость канала, при побитовой отправки, задается как
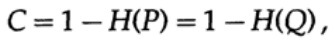
где, как и раньше, P — вероятность отсутствия ошибки в любом отправленном бите. При отправке n независимых битов емкость канала определяется как
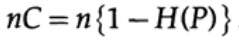
Если мы находимся рядом с пропускной способностью канала, то мы должны отправить почти такой объем информации для каждого из символов ai, i = 1, ..., М. С учётом того, что вероятностью возникновения каждого символа ai равна 1 / M, мы получим
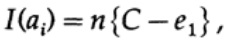
когда мы отправляем какое-либо из М равновероятных сообщений ai, мы имеем
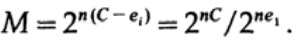
При отправке n бит мы ожидаем возникновение nQ ошибок. На практике, для сообщения состоящего из n-бит, мы будем иметь приблизительно nQ ошибок в полученном сообщении. При больших n, относительная вариация ( вариация = ширина распределения, )
распределения числа ошибок будет все более узкой с ростом n.
Итак, со стороны передатчика, я беру сообщение ai для отправки и рисую сферу вокруг него радиусом

который немного больше на величину равную e2, чем ожидаемое число ошибок Q, (рисунок 13.II). Если n достаточно велико, то существует сколь угодно малая вероятность появления точки сообщения bj на стороне приемника, которая выходит за пределы этой сферы. Зарисуем ситуацию, как вижу ее я с точки зрения передатчика: мы имеем любые радиусы от переданного сообщения ai к полученному сообщению bj с вероятностью ошибки равной (или почти равной) нормальному распределению, достигающего максимума в nQ. Для любого заданного e2 существует n настолько большое, что вероятность того, что полученная точка bj, выходящая за пределы моей сферы, будет настолько малой, насколько вам будет угодно.
Теперь рассмотрим эту же ситуацию с вашей стороны (рис. 13.III). На стороне приемника есть сфера S( r) того же радиуса r вокруг принятой точки bj в n-мерном пространстве, такая, что если принятое сообщение bj находится внутри моей сферы, тогда отправленное мной сообщение ai находится внутри вашей сферы.
Как может возникнуть ошибка? Ошибка может произойти в случаях, описанных в таблице ниже:

Рисунок 13.III

Здесь мы видим, что, если в сфере построенной вокруг принятой точки существует еще хотя бы еще одна точка, соответствующая возможному отправленному не закодированному сообщению, то при передачи произошла ошибка, так как вы не можете определить какое именно из этих сообщений было передано. Отправленное сообщение не содержит ошибки, только если точка, соответствующая ему, находится в сфере, и не существует других точек, возможных в данном коде, которые находятся в той же сфере.
Мы имеет математическое уравнение для вероятности ошибки Ре, если было отправлено сообщение ai

Мы можем выбросить первый множитель во втором слагаемом, приняв его за 1. Таким образом получим неравенство

Очевидно, что

следовательно
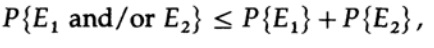
повторно применяем к последнему члену справа
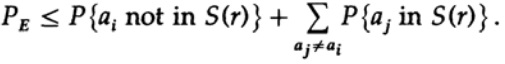
Приняв n достаточно большим, первый член может быть принят сколь угодно малым, скажем, меньше некоторого числа d. Поэтому мы имеем
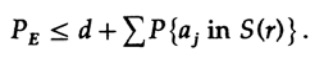
Теперь рассмотрим, как можно построить код простой замены для кодирования M сообщений, состоящих из n бит. Не имея представления о том, как именно строить код (коды с коррекцией ошибки еще не были изобретены), Шеннон выбрал случайное кодирование. Подбросьте монетку для каждого из n битов в сообщении и повторите процесс для М сообщений. Всего нужно сделать nM бросков монеты, поэтому возможны

кодовых словарей, имеющие одинаковую вероятность ½nM. Конечно, случайный процесс создания кодового словаря означает, что есть вероятность появления дубликатов, а также кодовых точек, которые будут близки друг к другу и, следовательно, будут источником вероятных ошибок. Нужно доказать, что если это не происходит с вероятностью выше, чем любой небольшой выбранный уровень ошибки, то заданное n достаточно велико.
Решающим момент заключается в том, что Шеннон усреднил все возможные кодовые книги, чтобы найти среднюю ошибку! Мы будем использовать символ Av [.], чтобы обозначить среднее значение по множеству всех возможных случайных кодовых словарей. Усреднение по константе d, конечно, дает константу, так как для усреднения каждый член совпадает с любым другим членом в сумме,
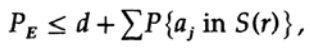
который может быть увеличен (M–1 переходит в M )
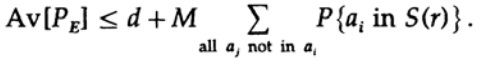
Для любого конкретного сообщения, при усреднении всех кодовых книг, кодирование пробегает все возможные значения, поэтому средняя вероятность того, что точка находится в сфере, — это отношение объема сферы к общему объему пространства. Объем сферы при этом

где s=Q+e2 <1/2 и ns должно быть целым числом.
Последнее справа слагаемое является наибольшим в этой сумме. Сначала оценим его значение по формуле Стирлинга для факториалов. Затем мы посмотрим на коэффициент уменьшения слагаемого перед ним, обратите внимание, что этот коэффициент увеличивается при перемещении влево, и поэтому мы можем: (1) ограничить значение суммы суммой геометрической прогрессии с этим начальным коэффициентом, (2) расширить геометрическую прогрессию с ns членов до бесконечного числа членов,(3) посчитать сумму бесконечной геометрической прогрессии (стандартная алгебра, ничего существенного) и наконец получить предельное значение (для достаточного большого n):
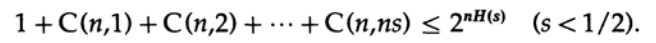
Обратите внимание, как энтропия H(s) появилась в биномиальном тождестве. Заметьте, что разложение в ряд Тейлора H(s)=H(Q+e2) дает оценку, полученную с учётом только первой производной и игнорировании всех остальных. Теперь соберем конечное выражение:
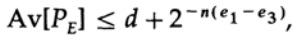
где
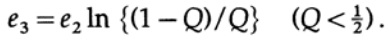
Все, что нам нужно сделать, это выбрать e2, так чтобы e3 < e1, и тогда последний член будет сколь угодно малым, при достаточно большом n. Следовательно, средняя ошибка PE может быть получена сколь угодно малой при пропускной способности канала сколь угодно близкой к C.
Если среднее значение по всем кодам имеет достаточно малую ошибку, то по меньшей мере один код должен быть подходящим, следовательно, существует по меньшей мере одна подходящая система кодирования. Это важный результат, полученный Шенноном — «теорема Шеннона для канала с помехами», хотя следует заметить, что он доказал это для гораздо более общего случая, чем для простого двоичного симметричного канала, использованного мной. Для общего случая математические выкладки намного сложнее, но идеи не так уж различны, поэтому очень часто на примере частного случая можно раскрыть истинный смысл теоремы.
Давайте покритикуем результат. Мы неоднократно повторяли: «При достаточно больших n». Но насколько большое значение n? Очень, очень большое, если вы на самом деле хотите быть одновременно близки к пропускной способности канала и быть уверены в корректной передачи данных! Настолько большим, что фактически вы будете вынуждены ждать очень долго, чтобы накопить сообщение из такого количества бит, чтобы в последствии закодировать его. При этом размер словаря случайного кода будет просто огромным (ведь такой словарь нельзя представить в более короткой форме, чем полный список всех Mn битов, при том что n и M очень велики)!
Коды коррекции ошибок избегают ожидания очень длинного сообщения, с его последующим кодированием и декодированием через очень большие кодовые книги, потому что они избегают кодовых книг как таковых и используют вместо них обычные вычисления. В простой теории такие коды, как правило, теряют способность приблизиться к пропускной способности канала и вместе с тем сохранить достаточно низкую частоту ошибок, но, когда код исправляет большое количество ошибок, они показывают хорошие результаты. Другими словами, если вы закладываете какую-то ёмкость канала для исправления ошибок, то вы должны использовать возможность исправления ошибки большую часть времени, т. е в каждом отправленном сообщении должно быть исправлено большое количество ошибок, иначе вы теряете эту емкость впустую.
При этом доказанная выше теорема все равно не бессмысленна! Она показывает, что эффективные системы передачи должны использовать продуманные схемы кодирования очень длинных битовых строк. Примером являются спутники, которые улетели за пределы внешних планеты; по мере удаления от Земли и Солнца они вынуждены исправлять все большее и большее количество ошибок в блоке данных: некоторые спутники используют солнечные батареи, которые дают около 5 Вт, другие используют атомные источники питания, дающие примерно ту же мощность. Слабая мощность источника питания, небольшие размеры тарелок передатчиков и ограниченные размеры тарелок приемников на Земле, огромное расстояние, которое должен преодолеть сигнал — все это требует использования кодов с высоким уровнем коррекции ошибок для построения эффективной системы связи.
Вернемся к n-мерному пространству, которое мы использовали в доказательстве выше. Обсуждая его, мы показали, что почти весь объем сферы сосредоточен около внешней поверхности, — таким образом, почти наверняка отправленный сигнал будет располагаться у поверхности сферы, построенной вокруг принятого сигнала, даже при относительно небольшом радиусе такой сферы. Поэтому не удивительно, что принятый сигнал после исправления произвольно большого количества ошибок, nQ, оказывается сколь угодно близок к сигналу без ошибок. Емкость канала связи, которую мы рассмотрели ранее, является ключом к пониманию этого явления. Обратите внимание, что подобные сферы, построенные для кодов Хэмминга с исправлением ошибок, не перекрывают друг друга. Большое количество практически ортогональных измерений в n-мерном пространстве показывают, почему мы можем уместить M сфер в пространстве с небольшим перекрытием. Если допустить небольшое, сколь угодно малое перекрытие, которые может приводить только к небольшому количеству ошибок при декодировании можно получить плотное размещение сфер в пространстве. Хэмминг гарантировал определенный уровень исправления ошибок, Шеннон — низкую вероятность ошибки, но при этом сохранение фактической пропускной способности сколь угодно близкой к емкости канала связи, чего коды Хэмминга сделать не могут.
Теория информации не говорит о том, как спроектировать эффективную систему, но она указывает направление движения в сторону эффективных систем связи. Это ценный инструмент для построения систем связи между машинами, но, как отмечалось ранее, она не имеет особого отношения к тому, как люди обмениваются информацией между собой. Степень, в которой биологическое наследование подобно техническим системам связи, попросту неизвестна, поэтому в настоящий момент не понятно, насколько теория информации применима к генам. Нам не остается ничего другого, как просто попробовать, и если успех покажет нам машино-подобный характер этого явления, то неудача укажет на другие существенные аспекты природы информации.
Давайте не много отвлечемся. Мы видели, что все первоначальные определения, в большей или меньшей степени, должны выражать сущность наших изначальных убеждений, но им свойственна некоторая степень искажения, и поэтому они оказываются не применимы. Традиционно принято, что, в конечном счете, определение, которое мы используем, фактически определяет суть; но, это лишь указывает нам, как обрабатывать вещи и никоим образом не несет нам никакого смысла. Постулационный подход, столь сильно одобряемый в математических кругах, оставляет желать лучшего на практике.
Теперь мы рассмотрим пример тестов на IQ, где определение является настолько циклическим, насколько вам это угодно, и как следствие вводит вас в заблуждение. Создается тест, который, как предполагается, должен измерить интеллект. После он пересматривается, что быть сделать его максимально последовательным, насколько это возможно, а затем его публикуют и простым методом калибруют таким образом, чтобы измеряемый «интеллект» оказался нормально распределенным (конечно же по кривой калибровке). Все определения должны перепроверяться, не только когда они впервые предложены, но и намного позже, когда они используются в сделанных выводах. В какой степени границы определений подходят для решаемой задачи? Как часто определения, данные в одних условиях, начинают применяться в достаточно отличающихся условиях? Такое встречается достаточно часто! В гуманитарных науках, с которыми вы неизбежно столкнётесь в вашей жизни, это происходит чаще.
Таким образом, одной из целей этой презентации теории информации, помимо демонстрации ее полезности, являлось предупреждение вас об этой опасности, или демонстрация того, как именно ее использовать для получения желаемого результата. Давно замечено, что первоначальные определения обуславливают то, что вы находите в итоге, в гораздо в большей мере, чем кажется. Первоначальные определения требуют от вас большого внимания не только в любой новой ситуации, но и в областях, с которыми вы давно работаете. Это позволит вам понять, в какой мере полученные результаты являются тавтологией, а не чем-то полезным.
Известная история Эддингтона повествует о людях, которые ловили рыбу в море с сетью. Изучив размер рыб, которые они поймали, они определили минимальный размер рыбы, которая водится в море! Их вывод был обусловлен используемым инструментом, а не действительностью.
Продолжение следует...
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru
Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)
Особо ищем тех, кто поможет перевести бонусную главу, которая есть только на видео. (переводим по 10 минут, первые 20 уже взяли)
«Цель этого курса — подготовить вас к вашему техническому будущему.»
 Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2588 в закладки, 429k прочтений)?
Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2588 в закладки, 429k прочтений)?Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
За перевод спасибо Андрею Пахомову.
Теория Информации была разработана К. Э. Шенноном в конце 1940х годов. Руководство Лабораторий Белла настаивало, чтобы он назвал ее «Теория Связи», т.к. это намного более точное название. По очевидным причинам, название «Теория Информации» обладает значительно большим воздействием на публику, поэтому Шеннон выбрал именно его, и именно оно известно нам по сей день. Само название предполагает, что теория имеет дело с информацией, это и делает ее важной, поскольку мы все глубже проникаем в информационную эпоху. В этой главе я затрону несколько основных выводов из этой теории, приведу не строгие, а скорее интуитивно понятные доказательства некоторых отдельных положений этой теории, чтобы вы поняли, чем на самом деле является «Теория Информации», где вы можете ее применять, а где нет.
Прежде всего, что такое “информация”? Шеннон отождествляет информацию с неопределенностью. Он выбрал отрицательный логарифм вероятности события в качестве количественной меры информации, которую вы получаете при наступлении события с вероятностью p. Например, если я скажу вам, что в Лос-Анжелесе туманная погода, тогда р близок к 1, что по большому счету, не дает нам много информации. Но если я скажу, что в июне в Монтерей идет дождь, то в этом сообщении будет присутствовать неопределенность, и оно будет содержать в себе больше информации. Достоверное событие не содержит в себе никакой информации, поскольку log 1 = 0.
Остановимся на этом подробнее. Шеннон полагал, что количественная мера информации должна быть непрерывной функцией от вероятности события p, а для независимых событий она должна быть аддитивной – количество информации, полученное в результате осуществления двух независимых событий, должно равняться количеству информации, полученному в результате осуществления совместного события. Например, результат броска игральных костей и монеты обычно рассматриваются как независимые события. Переведем вышесказанное на язык математики. Если I (p) – это количество информации, которое содержится в событии с вероятностью p, то, для совместного события, состоящего из двух независимых событий x с вероятностью p1 и y с вероятностью p2 получаем

(x и y независимые события)
Это функциональное уравнение Коши, истинное для всех p1 и p2. Для решения этого функционального уравнения предположим, что
p1 = p2 = p,
это дает

Если p1 = p2 и p2 = p, тогда

и т.д. Расширяя этот процесс, используя стандартный метод для экспонент, для всех рациональных чисел m / n, верно следующее
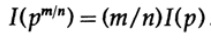
Из предполагаемой непрерывности информационной меры, следует, что логарифмическая функция является единственным непрерывным решением функционального уравнения Коши.
В теории информации принято принимать основание логарифма равное 2, поэтому бинарный выбор содержит ровно 1 бит информации. Следовательно, информация измеряется по формуле

Давайте приостановимся и разберемся, что же произошло выше. Прежде всего, мы так и не дали определение понятию “информация”, мы просто определили формулу ее количественной меры.
Во-вторых, эта мера зависит от неопределенности, и, хотя она в достаточной степени подходит для машин — например, телефонных системы, радио, телевидения, компьютеров и т. д. — она не отражает нормального человеческого отношения к информации.
В-третьих, это относительная мера, она зависит от текущего состояния вашего знания. Если вы смотрите на поток “случайных чисел” из генератора случайных чисел, вы предполагаете, что каждое следующее число неопределенно, но, если вы знаете формулу для вычисления «случайных чисел», следующее число будет известно, и, соответственно, не будет содержать в себе информации.
Таким образом, определение, данное Шенноном для информации, во многих случаях подходит для машин, но, похоже, не соответствует человеческому пониманию этого слова. Именно по этой причине «Теорию информации» следовало назвать «Теорией связи». Тем не менее, уже слишком поздно чтобы менять определения (благодаря которым теория приобрела свою первоначальную популярность, и которые все еще заставляют людей думать, что эта теория имеет дело с «информацией»), поэтому мы вынуждены с ними смириться, но при этом вы должны чётко понимать, насколько определение информации, данное Шенноном, далеко от своего общеупотребительного смысла. Информация Шеннона имеет дело с чем-то совершенно другим, а именно с неопределенностью.
Вот о чем нужно подумать, когда вы предлагаете какую-либо терминологию. Насколько предложенное определение, например, определение информации данное Шенноном, согласуется с вашей первоначальной идеей и насколько оно отличается? Почти нет термина, который бы в точности отражал ваше ранее видение концепции, но в конечном итоге, именно используемая терминология отражает смысл концепции, поэтому формализация чего-то посредством чётких определений всегда вносит некоторый шум.
Рассмотрим систему, алфавит которой состоит из символов q с вероятностями pi. В этом случае среднее количество информации в системе (её ожидаемое значение) равно:
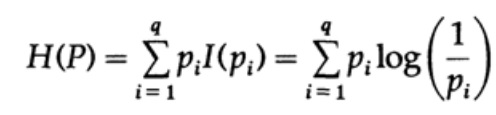
Это называется энтропией системы с распределением вероятности {pi}. Мы используем термин «энтропия», потому что та же самая математическая форма возникает в термодинамике и статистической механике. Именно поэтому термин «энтропия» создает вокруг себя некую ауру важности, которая, в конечном счете, не оправдана. Одинаковая математическая форма записи не подразумевает одинаковой интерпретации символов!
Энтропия распределения вероятности играет главную роль в теории кодирования. Неравенство Гиббса для двух разных распределений вероятности pi и qi является одним из важных следствий этой теории. Итак, мы должны доказать, что
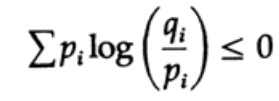
Доказательство опирается на очевидный график, рис. 13.I, который показывает, что
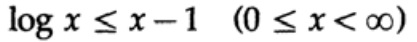
а равенство достигается только при x = 1. Применим неравенство к каждому слагаемому суммы из левой части:

Если алфавит системы связи состоит из q символов, то принимая вероятность передачи каждого символа qi = 1/q и подставляя q, получаем из неравенства Гиббса


Рисунок 13.I
Это говорит о том, что если вероятность передачи всех q символов одинакова и равна — 1 / q, то максимальная энтропия равна ln q, в противном случае выполняется неравенство.
В случае однозначно декодируемого кода, мы имеем неравенство Крафта
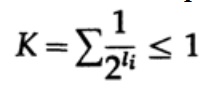
Теперь если мы определим псевдовероятности

где конечно
 = 1, что следует из неравенства Гиббса,
= 1, что следует из неравенства Гиббса,
и применим немного алгебры (помните, что K ≤ 1, поэтому мы можем опустить логарифмический член, и возможно, усилить неравенство позже), то получим

где L — это средняя длина кода.
Таким образом, энтропия является минимальной границей для любого посимвольного кода со средней длиной кодового слова L. Это теорема Шеннона для канала без помех.
Теперь рассмотрим главную теорему об ограничениях систем связи, в которых информация передаётся в виде потока независимых бит и присутствует шум. Подразумевается, что вероятность корректной передачи одного бита P > 1 / 2, а вероятность того, что значение бита будет инвертировано при передачи (произойдет ошибка) равняется Q = 1 — P. Для удобства предположим, что ошибки независимы и вероятность ошибки одинакова для каждого отправленного бита — то есть в канале связи присутствует «белый шум».
Путь мы имеем длинный поток из n бит, закодированные в одно сообщение — n — мерное расширение однобитового кода. Значение n мы определим позже. Рассмотрим сообщение, состоящее из n-битов как точку в n-мерном пространстве. Поскольку у нас есть n-мерное пространство — и для простоты будем предполагать, что каждое сообщение имеет одинаковую вероятность возникновения — существует M возможных сообщений (M также будет определено позже), следовательно, вероятность любого оправленного сообщения равняется
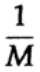

(отправитель)
График 13.II
Далее рассмотрим идею о пропускной способности канала. Не вдаваясь в подробности, пропускная способность канала определяется как максимальный объем информации, который может быть надежно передан по каналу связи, с учётом использования максимально эффективного кодирования. Нет доводов в пользу того, что через канал связи может быть передано больше информации, чем его емкость. Это можно доказать для бинарного симметричного канала (который мы используем в нашем случае). Емкость канала, при побитовой отправки, задается как
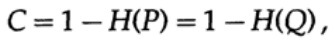
где, как и раньше, P — вероятность отсутствия ошибки в любом отправленном бите. При отправке n независимых битов емкость канала определяется как
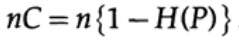
Если мы находимся рядом с пропускной способностью канала, то мы должны отправить почти такой объем информации для каждого из символов ai, i = 1, ..., М. С учётом того, что вероятностью возникновения каждого символа ai равна 1 / M, мы получим
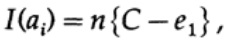
когда мы отправляем какое-либо из М равновероятных сообщений ai, мы имеем
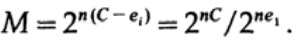
При отправке n бит мы ожидаем возникновение nQ ошибок. На практике, для сообщения состоящего из n-бит, мы будем иметь приблизительно nQ ошибок в полученном сообщении. При больших n, относительная вариация ( вариация = ширина распределения, )
распределения числа ошибок будет все более узкой с ростом n.
Итак, со стороны передатчика, я беру сообщение ai для отправки и рисую сферу вокруг него радиусом

который немного больше на величину равную e2, чем ожидаемое число ошибок Q, (рисунок 13.II). Если n достаточно велико, то существует сколь угодно малая вероятность появления точки сообщения bj на стороне приемника, которая выходит за пределы этой сферы. Зарисуем ситуацию, как вижу ее я с точки зрения передатчика: мы имеем любые радиусы от переданного сообщения ai к полученному сообщению bj с вероятностью ошибки равной (или почти равной) нормальному распределению, достигающего максимума в nQ. Для любого заданного e2 существует n настолько большое, что вероятность того, что полученная точка bj, выходящая за пределы моей сферы, будет настолько малой, насколько вам будет угодно.
Теперь рассмотрим эту же ситуацию с вашей стороны (рис. 13.III). На стороне приемника есть сфера S( r) того же радиуса r вокруг принятой точки bj в n-мерном пространстве, такая, что если принятое сообщение bj находится внутри моей сферы, тогда отправленное мной сообщение ai находится внутри вашей сферы.
Как может возникнуть ошибка? Ошибка может произойти в случаях, описанных в таблице ниже:

Рисунок 13.III

Здесь мы видим, что, если в сфере построенной вокруг принятой точки существует еще хотя бы еще одна точка, соответствующая возможному отправленному не закодированному сообщению, то при передачи произошла ошибка, так как вы не можете определить какое именно из этих сообщений было передано. Отправленное сообщение не содержит ошибки, только если точка, соответствующая ему, находится в сфере, и не существует других точек, возможных в данном коде, которые находятся в той же сфере.
Мы имеет математическое уравнение для вероятности ошибки Ре, если было отправлено сообщение ai

Мы можем выбросить первый множитель во втором слагаемом, приняв его за 1. Таким образом получим неравенство

Очевидно, что

следовательно
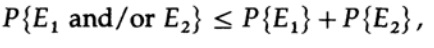
повторно применяем к последнему члену справа
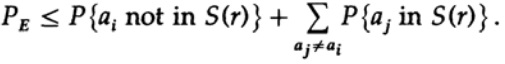
Приняв n достаточно большим, первый член может быть принят сколь угодно малым, скажем, меньше некоторого числа d. Поэтому мы имеем
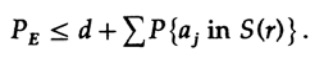
Теперь рассмотрим, как можно построить код простой замены для кодирования M сообщений, состоящих из n бит. Не имея представления о том, как именно строить код (коды с коррекцией ошибки еще не были изобретены), Шеннон выбрал случайное кодирование. Подбросьте монетку для каждого из n битов в сообщении и повторите процесс для М сообщений. Всего нужно сделать nM бросков монеты, поэтому возможны

кодовых словарей, имеющие одинаковую вероятность ½nM. Конечно, случайный процесс создания кодового словаря означает, что есть вероятность появления дубликатов, а также кодовых точек, которые будут близки друг к другу и, следовательно, будут источником вероятных ошибок. Нужно доказать, что если это не происходит с вероятностью выше, чем любой небольшой выбранный уровень ошибки, то заданное n достаточно велико.
Решающим момент заключается в том, что Шеннон усреднил все возможные кодовые книги, чтобы найти среднюю ошибку! Мы будем использовать символ Av [.], чтобы обозначить среднее значение по множеству всех возможных случайных кодовых словарей. Усреднение по константе d, конечно, дает константу, так как для усреднения каждый член совпадает с любым другим членом в сумме,
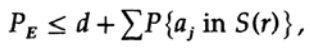
который может быть увеличен (M–1 переходит в M )
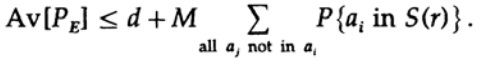
Для любого конкретного сообщения, при усреднении всех кодовых книг, кодирование пробегает все возможные значения, поэтому средняя вероятность того, что точка находится в сфере, — это отношение объема сферы к общему объему пространства. Объем сферы при этом

где s=Q+e2 <1/2 и ns должно быть целым числом.
Последнее справа слагаемое является наибольшим в этой сумме. Сначала оценим его значение по формуле Стирлинга для факториалов. Затем мы посмотрим на коэффициент уменьшения слагаемого перед ним, обратите внимание, что этот коэффициент увеличивается при перемещении влево, и поэтому мы можем: (1) ограничить значение суммы суммой геометрической прогрессии с этим начальным коэффициентом, (2) расширить геометрическую прогрессию с ns членов до бесконечного числа членов,(3) посчитать сумму бесконечной геометрической прогрессии (стандартная алгебра, ничего существенного) и наконец получить предельное значение (для достаточного большого n):
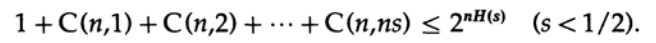
Обратите внимание, как энтропия H(s) появилась в биномиальном тождестве. Заметьте, что разложение в ряд Тейлора H(s)=H(Q+e2) дает оценку, полученную с учётом только первой производной и игнорировании всех остальных. Теперь соберем конечное выражение:
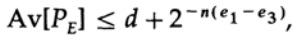
где
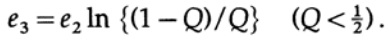
Все, что нам нужно сделать, это выбрать e2, так чтобы e3 < e1, и тогда последний член будет сколь угодно малым, при достаточно большом n. Следовательно, средняя ошибка PE может быть получена сколь угодно малой при пропускной способности канала сколь угодно близкой к C.
Если среднее значение по всем кодам имеет достаточно малую ошибку, то по меньшей мере один код должен быть подходящим, следовательно, существует по меньшей мере одна подходящая система кодирования. Это важный результат, полученный Шенноном — «теорема Шеннона для канала с помехами», хотя следует заметить, что он доказал это для гораздо более общего случая, чем для простого двоичного симметричного канала, использованного мной. Для общего случая математические выкладки намного сложнее, но идеи не так уж различны, поэтому очень часто на примере частного случая можно раскрыть истинный смысл теоремы.
Давайте покритикуем результат. Мы неоднократно повторяли: «При достаточно больших n». Но насколько большое значение n? Очень, очень большое, если вы на самом деле хотите быть одновременно близки к пропускной способности канала и быть уверены в корректной передачи данных! Настолько большим, что фактически вы будете вынуждены ждать очень долго, чтобы накопить сообщение из такого количества бит, чтобы в последствии закодировать его. При этом размер словаря случайного кода будет просто огромным (ведь такой словарь нельзя представить в более короткой форме, чем полный список всех Mn битов, при том что n и M очень велики)!
Коды коррекции ошибок избегают ожидания очень длинного сообщения, с его последующим кодированием и декодированием через очень большие кодовые книги, потому что они избегают кодовых книг как таковых и используют вместо них обычные вычисления. В простой теории такие коды, как правило, теряют способность приблизиться к пропускной способности канала и вместе с тем сохранить достаточно низкую частоту ошибок, но, когда код исправляет большое количество ошибок, они показывают хорошие результаты. Другими словами, если вы закладываете какую-то ёмкость канала для исправления ошибок, то вы должны использовать возможность исправления ошибки большую часть времени, т. е в каждом отправленном сообщении должно быть исправлено большое количество ошибок, иначе вы теряете эту емкость впустую.
При этом доказанная выше теорема все равно не бессмысленна! Она показывает, что эффективные системы передачи должны использовать продуманные схемы кодирования очень длинных битовых строк. Примером являются спутники, которые улетели за пределы внешних планеты; по мере удаления от Земли и Солнца они вынуждены исправлять все большее и большее количество ошибок в блоке данных: некоторые спутники используют солнечные батареи, которые дают около 5 Вт, другие используют атомные источники питания, дающие примерно ту же мощность. Слабая мощность источника питания, небольшие размеры тарелок передатчиков и ограниченные размеры тарелок приемников на Земле, огромное расстояние, которое должен преодолеть сигнал — все это требует использования кодов с высоким уровнем коррекции ошибок для построения эффективной системы связи.
Вернемся к n-мерному пространству, которое мы использовали в доказательстве выше. Обсуждая его, мы показали, что почти весь объем сферы сосредоточен около внешней поверхности, — таким образом, почти наверняка отправленный сигнал будет располагаться у поверхности сферы, построенной вокруг принятого сигнала, даже при относительно небольшом радиусе такой сферы. Поэтому не удивительно, что принятый сигнал после исправления произвольно большого количества ошибок, nQ, оказывается сколь угодно близок к сигналу без ошибок. Емкость канала связи, которую мы рассмотрели ранее, является ключом к пониманию этого явления. Обратите внимание, что подобные сферы, построенные для кодов Хэмминга с исправлением ошибок, не перекрывают друг друга. Большое количество практически ортогональных измерений в n-мерном пространстве показывают, почему мы можем уместить M сфер в пространстве с небольшим перекрытием. Если допустить небольшое, сколь угодно малое перекрытие, которые может приводить только к небольшому количеству ошибок при декодировании можно получить плотное размещение сфер в пространстве. Хэмминг гарантировал определенный уровень исправления ошибок, Шеннон — низкую вероятность ошибки, но при этом сохранение фактической пропускной способности сколь угодно близкой к емкости канала связи, чего коды Хэмминга сделать не могут.
Теория информации не говорит о том, как спроектировать эффективную систему, но она указывает направление движения в сторону эффективных систем связи. Это ценный инструмент для построения систем связи между машинами, но, как отмечалось ранее, она не имеет особого отношения к тому, как люди обмениваются информацией между собой. Степень, в которой биологическое наследование подобно техническим системам связи, попросту неизвестна, поэтому в настоящий момент не понятно, насколько теория информации применима к генам. Нам не остается ничего другого, как просто попробовать, и если успех покажет нам машино-подобный характер этого явления, то неудача укажет на другие существенные аспекты природы информации.
Давайте не много отвлечемся. Мы видели, что все первоначальные определения, в большей или меньшей степени, должны выражать сущность наших изначальных убеждений, но им свойственна некоторая степень искажения, и поэтому они оказываются не применимы. Традиционно принято, что, в конечном счете, определение, которое мы используем, фактически определяет суть; но, это лишь указывает нам, как обрабатывать вещи и никоим образом не несет нам никакого смысла. Постулационный подход, столь сильно одобряемый в математических кругах, оставляет желать лучшего на практике.
Теперь мы рассмотрим пример тестов на IQ, где определение является настолько циклическим, насколько вам это угодно, и как следствие вводит вас в заблуждение. Создается тест, который, как предполагается, должен измерить интеллект. После он пересматривается, что быть сделать его максимально последовательным, насколько это возможно, а затем его публикуют и простым методом калибруют таким образом, чтобы измеряемый «интеллект» оказался нормально распределенным (конечно же по кривой калибровке). Все определения должны перепроверяться, не только когда они впервые предложены, но и намного позже, когда они используются в сделанных выводах. В какой степени границы определений подходят для решаемой задачи? Как часто определения, данные в одних условиях, начинают применяться в достаточно отличающихся условиях? Такое встречается достаточно часто! В гуманитарных науках, с которыми вы неизбежно столкнётесь в вашей жизни, это происходит чаще.
Таким образом, одной из целей этой презентации теории информации, помимо демонстрации ее полезности, являлось предупреждение вас об этой опасности, или демонстрация того, как именно ее использовать для получения желаемого результата. Давно замечено, что первоначальные определения обуславливают то, что вы находите в итоге, в гораздо в большей мере, чем кажется. Первоначальные определения требуют от вас большого внимания не только в любой новой ситуации, но и в областях, с которыми вы давно работаете. Это позволит вам понять, в какой мере полученные результаты являются тавтологией, а не чем-то полезным.
Известная история Эддингтона повествует о людях, которые ловили рыбу в море с сетью. Изучив размер рыб, которые они поймали, они определили минимальный размер рыбы, которая водится в море! Их вывод был обусловлен используемым инструментом, а не действительностью.
Продолжение следует...
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru
Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)
Особо ищем тех, кто поможет перевести бонусную главу, которая есть только на видео. (переводим по 10 минут, первые 20 уже взяли)
Содержание книги и переведенные главы
Предисловие
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru
- Intro to The Art of Doing Science and Engineering: Learning to Learn (March 28, 1995) Перевод: Глава 1
- «Foundations of the Digital (Discrete) Revolution» (March 30, 1995) Глава 2. Основы цифровой (дискретной) революции
- «History of Computers — Hardware» (March 31, 1995) Глава 3. История компьютеров — железо
- «History of Computers — Software» (April 4, 1995) Глава 4. История компьютеров — Софт
- «History of Computers — Applications» (April 6, 1995) Глава 5. История компьютеров — практическое применение
- «Artificial Intelligence — Part I» (April 7, 1995) Глава 6. Искусственный интеллект — 1
- «Artificial Intelligence — Part II» (April 11, 1995) Глава 7. Искусственный интеллект — II
- «Artificial Intelligence III» (April 13, 1995) Глава 8. Искуственный интеллект-III
- «n-Dimensional Space» (April 14, 1995) Глава 9. N-мерное пространство
- «Coding Theory — The Representation of Information, Part I» (April 18, 1995) Глава 10. Теория кодирования — I
- «Coding Theory — The Representation of Information, Part II» (April 20, 1995) Глава 11. Теория кодирования — II
- «Error-Correcting Codes» (April 21, 1995) Глава 12. Коды с коррекцией ошибок
- «Information Theory» (April 25, 1995) Глава 13. Теория информации
- «Digital Filters, Part I» (April 27, 1995) Глава 14. Цифровые фильтры — 1
- «Digital Filters, Part II» (April 28, 1995) Глава 15. Цифровые фильтры — 2
- «Digital Filters, Part III» (May 2, 1995) Глава 16. Цифровые фильтры — 3
- «Digital Filters, Part IV» (May 4, 1995) Глава 17. Цифровые фильтры — IV
- «Simulation, Part I» (May 5, 1995) Глава 18. Моделирование — I
- «Simulation, Part II» (May 9, 1995) Глава 19. Моделирование — II
- «Simulation, Part III» (May 11, 1995) Глава 20. Моделирование — III
- «Fiber Optics» (May 12, 1995) Глава 21. Волоконная оптика
- «Computer Aided Instruction» (May 16, 1995) Глава 22. Обучение с помощью компьютера (CAI)
- «Mathematics» (May 18, 1995) Глава 23. Математика
- «Quantum Mechanics» (May 19, 1995) Глава 24. Квантовая механика
- «Creativity» (May 23, 1995). Перевод: Глава 25. Креативность
- «Experts» (May 25, 1995) Глава 26. Эксперты
- «Unreliable Data» (May 26, 1995) Глава 27. Недостоверные данные
- «Systems Engineering» (May 30, 1995) Глава 28. Системная Инженерия
- «You Get What You Measure» (June 1, 1995) Глава 29. Вы получаете то, что вы измеряете
- «How Do We Know What We Know» (June 2, 1995) переводим по 10 минутным кусочкам
- Hamming, «You and Your Research» (June 6, 1995). Перевод: Вы и ваша работа
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru