Ряд моих коллег сталкиваются с проблемой, что для расчета какой-то метрики, например, коэффициента конверсии, приходится кверить всю базу данных. Или нужно провести детальное исследование по каждому клиенту, где клиентов миллионы. Такого рода квери могут работать довольно долго, даже в специально сделанных для этого хранилищах. Не очень-то прикольно ждать по 5-15-40 минут, пока считается простая метрика, чтобы выяснить, что тебе нужно посчитать что-то другое или добавить что-то еще.
Одним из решений этой проблемы является сэмплирование: мы не пытаемся вычислить нашу метрику на всем массиве данных, а берем подмножество, которое репрезентативно представляет нам нужные метрики. Это сэмпл может быть в 1000 раз меньше нашего массива данных, но при этом достаточно хорошо показывать нужные нам цифры.
В этой статье я решил продемонстрировать, как размеры выборки сэмплирования влияют на ошибку конечной метрики.
Проблема
Ключевой вопрос: насколько хорошо сэмпл описывает "генеральную совокупность"? Раз мы берем сэмпл с общего массива, то получаемые нами метрики оказываются случайными величинами. Разные сэмплы дадут нам разные результаты метрик. Разные, не значит любые. Теория вероятности говорит нам, что получаемые сэмплированием значения метрики должны группироваться вокруг истинного значения метрики (сделанного по всей выборке) с определенным уровнем ошибки. При этом у нас часто бывают задачи, где для решения можно обойтись разным уровнем ошибки. Одно дело прикинуть, получаем ли мы конверсию 50% или 10%, а другое дело получить результат с точностью 50.01% vs 50.02%.
Интересно, что с точки зрения теории, наблюдаемый нами коэффициент конверсии по всей выборке — это тоже случайная величина, т.к. "теоретический" коэффициент конверсии можно посчитать только на выборке бесконечного размера. Это означает, что даже все наши наблюдения в БД на самом деле дают оценку конверсии со своей точностью, хотя нам кажется, что вот эти наши подсчитанные цифры абсолютно точны. Это так же приводит к выводу, что даже если сегодня коэффициент конверсии отличается от вчерашнего, то это еще не означает, что у нас что-то поменялось, а лишь означает, что сегодняшний сэмпл (все наблюдения в БД) из генеральной совокупности (все возможные наблюдения за этот день, которые произошли и не произошли) дал несколько иной результат, чем вчерашний. Во всяком случае для любого честного продукта или аналитика это должно быть базовой гипотезой.
Формулировка задачи
Допустим у нас 1 000 000 записей в БД вида 0/1, которые говорят нам о том, случилась ли конверсия по событию. Тогда коэффициент конверсии это просто сумма 1 делить на 1 млн.
Вопрос: если мы возьмем выборку размером N, то на сколько и с какой вероятностью будет отличатся коэффициент конверсии от посчитанного по всей выборке?
Теоретические рассуждения
Задача сводится к расчету доверительного интервала коэффициента конверсии по выборке заданного размера для биноминального распределения.
Из теории стандартное отклонение для биноминального распределения это:
S = sqrt(p * (1 — p) /N)
Где
p — коэффициент конверсии
N — Размер выборки
S — стандартное отклонение
Непосредственно доверительный интервал я считать из теории не стану. Там довольно сложный и запутанный матан, который в итоге связывает стандартное отклонение и конечную оценку доверительного интервала.
Давайте разовьем "интуицию" по поводу формулы стандартного отклонения:
- Чем больше размер сэмпла, тем меньше ошибка. При этом ошибка падает в обратной квадратичной зависимости, т.е. увеличение выборки в 4 раза увеличивает точность лишь в 2 раза. Это означает, что в какой-то момент наращивание размера сэмпла не даст особых преимуществ, а так же означает, что довольно высокую точность можно получить достаточно маленькой выборкой.

- Есть зависимость ошибки от величины коэффициента конверсии. Относительная ошибка (т.е. отношение ошибки к величине коэффициента конверсии) имеет "мерзкую" тенденции быть тем больше, чем ниже коэффициент конверсии:
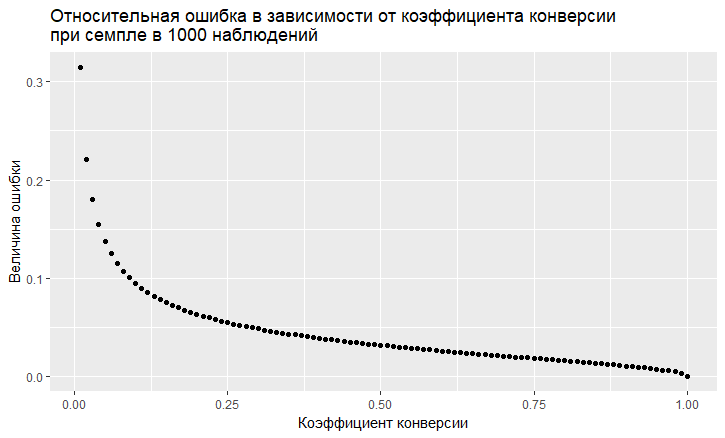
- Как мы видим, ошибка "взлетает" в небеса при низком коэффициенте конверсии. Это означает, что если вы сэмплируете редкие события, то вам нужны большие размеры выборки, иначе вы получите оценку конверсии с очень большой ошибкой.
Моделирование
Мы можем полностью отойти от теоретического решения и решить задачу "в лоб". Благодаря языку R теперь это сделать очень просто. Чтобы ответить на вопрос, в какую мы ошибку получим при сэмплировании, можно просто сделать тысячу сэмплирований и посмотреть, какую ошибку мы получаем.
Подход такой:
- Берем разные коэффициенты конверсии (от 0.01% до 50%).
- Берем 1000 сэмплов по 10, 100, 1000, 10000, 50000, 100000, 250000, 500000 элементов в выборке
- Считаем коэффициент конверсии по каждой группе сэмплов (1000 коэффициентов)
- Строим гистограмму по каждой группе сэмплов и определяем, в каких пределах лежат 60%, 80% и 90% наблюдаемых коэффициентов конверсии.
Код на R генерирующий данные:
sample.size <- c(10, 100, 1000, 10000, 50000, 100000, 250000, 500000)
bootstrap = 1000
Error <- NULL
len = 1000000
for (prob in c(0.0001, 0.001, 0.01, 0.1, 0.5)){
CRsub <- data.table(sample_size = 0, CR = 0)
v1 = seq(1,len)
v2 = rbinom(len, 1, prob)
set = data.table(index = v1, conv = v2)
print(paste('probability is: ', prob))
for (j in 1:length(sample.size)){
for(i in 1:bootstrap){
ss <- sample.size[j]
subset <- set[round(runif(ss, min = 1, max = len),0),]
CRsample <- sum(subset$conv)/dim(subset)[1]
CRsub <- rbind(CRsub, data.table(sample_size = ss, CR = CRsample))
}
print(paste('sample size is:', sample.size[j]))
q <- quantile(CRsub[sample_size == ss, CR], probs = c(0.05,0.1, 0.2, 0.8, 0.9, 0.95))
Error <- rbind(Error, cbind(prob,ss,t(q)))
}В результате мы получаем следующую таблицу (дальше будут графики, но детали лучше видны в таблице).
| Коэффициент конверсии | Размер сэмпла | 5% | 10% | 20% | 80% | 90% | 95% |
|---|---|---|---|---|---|---|---|
| 0.0001 | 10 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.0001 | 100 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.0001 | 1000 | 0 | 0 | 0 | 0 | 0 | 0.001 |
| 0.0001 | 10000 | 0 | 0 | 0 | 0.0002 | 0.0002 | 0.0003 |
| 0.0001 | 50000 | 0.00004 | 0.00004 | 0.00006 | 0.00014 | 0.00016 | 0.00018 |
| 0.0001 | 100000 | 0.00005 | 0.00006 | 0.00007 | 0.00013 | 0.00014 | 0.00016 |
| 0.0001 | 250000 | 0.000072 | 0.0000796 | 0.000088 | 0.00012 | 0.000128 | 0.000136 |
| 0.0001 | 500000 | 0.00008 | 0.000084 | 0.000092 | 0.000114 | 0.000122 | 0.000128 |
| 0.001 | 10 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.001 | 100 | 0 | 0 | 0 | 0 | 0 | 0.01 |
| 0.001 | 1000 | 0 | 0 | 0 | 0.002 | 0.002 | 0.003 |
| 0.001 | 10000 | 0.0005 | 0.0006 | 0.0007 | 0.0013 | 0.0014 | 0.0016 |
| 0.001 | 50000 | 0.0008 | 0.000858 | 0.00092 | 0.00116 | 0.00122 | 0.00126 |
| 0.001 | 100000 | 0.00087 | 0.00091 | 0.00095 | 0.00112 | 0.00116 | 0.0012105 |
| 0.001 | 250000 | 0.00092 | 0.000948 | 0.000972 | 0.001084 | 0.001116 | 0.0011362 |
| 0.001 | 500000 | 0.000952 | 0.0009698 | 0.000988 | 0.001066 | 0.001086 | 0.0011041 |
| 0.01 | 10 | 0 | 0 | 0 | 0 | 0 | 0.1 |
| 0.01 | 100 | 0 | 0 | 0 | 0.02 | 0.02 | 0.03 |
| 0.01 | 1000 | 0.006 | 0.006 | 0.008 | 0.013 | 0.014 | 0.015 |
| 0.01 | 10000 | 0.0086 | 0.0089 | 0.0092 | 0.0109 | 0.0114 | 0.0118 |
| 0.01 | 50000 | 0.0093 | 0.0095 | 0.0097 | 0.0104 | 0.0106 | 0.0108 |
| 0.01 | 100000 | 0.0095 | 0.0096 | 0.0098 | 0.0103 | 0.0104 | 0.0106 |
| 0.01 | 250000 | 0.0097 | 0.0098 | 0.0099 | 0.0102 | 0.0103 | 0.0104 |
| 0.01 | 500000 | 0.0098 | 0.0099 | 0.0099 | 0.0102 | 0.0102 | 0.0103 |
| 0.1 | 10 | 0 | 0 | 0 | 0.2 | 0.2 | 0.3 |
| 0.1 | 100 | 0.05 | 0.06 | 0.07 | 0.13 | 0.14 | 0.15 |
| 0.1 | 1000 | 0.086 | 0.0889 | 0.093 | 0.108 | 0.1121 | 0.117 |
| 0.1 | 10000 | 0.0954 | 0.0963 | 0.0979 | 0.1028 | 0.1041 | 0.1055 |
| 0.1 | 50000 | 0.098 | 0.0986 | 0.0992 | 0.1014 | 0.1019 | 0.1024 |
| 0.1 | 100000 | 0.0987 | 0.099 | 0.0994 | 0.1011 | 0.1014 | 0.1018 |
| 0.1 | 250000 | 0.0993 | 0.0995 | 0.0998 | 0.1008 | 0.1011 | 0.1013 |
| 0.1 | 500000 | 0.0996 | 0.0998 | 0.1 | 0.1007 | 0.1009 | 0.101 |
| 0.5 | 10 | 0.2 | 0.3 | 0.4 | 0.6 | 0.7 | 0.8 |
| 0.5 | 100 | 0.42 | 0.44 | 0.46 | 0.54 | 0.56 | 0.58 |
| 0.5 | 1000 | 0.473 | 0.478 | 0.486 | 0.513 | 0.52 | 0.525 |
| 0.5 | 10000 | 0.4922 | 0.4939 | 0.4959 | 0.5044 | 0.5061 | 0.5078 |
| 0.5 | 50000 | 0.4962 | 0.4968 | 0.4978 | 0.5018 | 0.5028 | 0.5036 |
| 0.5 | 100000 | 0.4974 | 0.4979 | 0.4986 | 0.5014 | 0.5021 | 0.5027 |
| 0.5 | 250000 | 0.4984 | 0.4987 | 0.4992 | 0.5008 | 0.5013 | 0.5017 |
| 0.5 | 500000 | 0.4988 | 0.4991 | 0.4994 | 0.5006 | 0.5009 | 0.5011 |
Посмотрим случаи с 10% конверсией и с низкой 0.01% конверсией, т.к. на них хорошо видны все особенности работы с сэмплированием.
При 10% конверсии картина выглядит довольно простой:

Точки — это края 5-95% доверительного интервала, т.е. делая сэмпл мы будем в 90% случаев получать CR на выборке внутри этого интервала. Вертикальная шкала — размер сэмпла (шкала логарифмическая), горизонтальная — значение коэффициента конверсии. Вертикальная черта — "истинный" CR.
Мы тут видим то же, что мы видели из теоретической модели: точность растет по мере роста размера сэмпла, при этом одна довольно быстро "сходится" и сэмпл получает результат близкий к "истинному". Всего на 1000 сэмпле мы имеем 8.6% — 11.7%, что для ряда задач будет достаточно. А на 10 тысячах уже 9.5% — 10.55%.
Куда хуже дела обстоят с редкими событиями и это согласуется с теорией:

У низкого коэффициента конверсии в 0.01% принципе проблемы на статистике в 1 млн наблюдений, а с сэмплами ситуация оказывается еще хуже. Ошибка становится просто гигантской. На сэмплах до 10 000 метрика в принципе не валидна. Например, на сэмпле в 10 наблюдений мой генератор просто 1000 раз получил 0 конверсию, поэтому там только 1 точка. На 100 тысячах мы имеем разброс от 0.005% до 0.0016%, т.е мы можем ошибаться почти в половину коэффициента при таком сэмплировании.
Также стоит отметить, что когда вы наблюдаете конверсию такого маленького масштаба на 1 млн испытаний, то у вас просто большая натуральная ошибка. Из этого следует, что выводы по динамике таких редких событий надо делать на действительно больших выборках иначе вы просто гоняетесь за призраками, за случайными флуктуациями в данных.
Выводы:
- Сэмплирование рабочий метод для получения оценок
- Точность сэмплов растет при росте размера сэмпла и падает при снижении коэффициента конверсии.
- Точность оценок можно смоделировать для вашей задачи и таким образом подобрать оптимальное сэмплирование для себя
- Важно помнить, что редкие события плохо сэмплируют
- В целом редкие события трудно анализировать, они без сэмплов требуют больших выборок данных.




