Симуляция физических явлений с VPython

В физических науках часто допускают упрощения и приблизительные значения: орбиты всегда круговые, снаряды летят без сопротивления воздуха, а маятник отклоняется только на небольшой угол. 

Подобные упрощения необходимы и уместны, когда вы пытаетесь усвоить основные законы природы впервые. Приблизительные значения полезны тем, что при небольших потерях в точности, мы экономим много времени (например, как при вычислении магнитного момента). Но мир намного сложнее и интереснее, а главная цель физики — понять реальный мир.

К счастью, компьютеры могут выполнять объемные и сложные вычисления за короткий промежуток времени. VPython позволяет моделировать сложные физические процессы и создавать 3D-анимации с возможностью навигации в режиме реального времени.

VPython можно установить, используя Jupyter notebook, 3D-сцена появится прямо там. Если код запускается вне notebook (например, из командной строки или IDLE), откроется окно браузера, отображающее сцену. Internet Explorer не поддерживает, рекомендуется использовать браузер Chrome, так как здесь будет более расширенная информация о возможных ошибках.

С чего начать?

Пакет опубликован на Pypi, и его можно легко установить с помощью pip:

pip install vpython

После завершения установки можно попробовать создать 3D Cylinder (Цилиндр):

import vpython as vpvp.cylinder()

Чтобы изменить положение, размер и цвет:

vp.cylinder(pos=vp.vector( 4, 0, 0), size=vp.vector(4,4,4), color = vp.color.red)

Моделирование Солнечной системы

Закон всемирного тяготения — один из самых важных в физике. С его помощью можно вычислить, с какой скоростью Луна движется вокруг Земли, как вывести спутник на орбиту, а также обнаружить темную материю и черные дыры.

Один из способов изучения силы притяжения — использовать метода Эйлера — Кромера. Предположим, мы хотим исследовать орбиту планеты, которая вращается вокруг звезды, и для программирования гравитации между планетой и звездой требуется всего несколько математических шагов.

• Во-первых, в начале уравнения поставим минус, что будет означать, что сила гравитации всегда притягивает.

• Во-вторых, гравитационная постоянная. Это константа, ее значение всегда одинаково, независимо от того, где именно во Вселенной вы находитесь.

• Затем мы умножаем массу звезды на массу планеты.

• Далее нам нужно найти расстояние между звездой и планетой. Мы можем получить вектор расстояния, вычитая одну позицию из другой. Величина вектора расстояния идет в знаменатель.

• Наконец, мы вычисляем вектор “R с крышкой”, который задает направление гравитационной силы. Мы можем вычислить “R с крышкой”, с помощью следующей формулы:

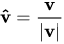
Кодинг

Начнем работу с написания нового Python-скрипта, импорта модуля и создания  сцены.

Сначала импортируйте модуль, затем сгенерируйте сцену:

import vpython as vp
vp.scene.title = "Modeling the motion of planets with the gravitational force"
vp.scene.height = 600
vp.scene.width = 800

Создадим звезду и планету (вы можете изменить массу на реальное значение):

planet = vp.sphere(pos=vp.vector(1,0,0), radius=0.05, color=vp.color.green,
               mass = 1, momentum=vp.vector(0,30,0), make_trail=True )

star = vp.sphere(pos=vp.vector(0,0,0), radius=0.2, color=vp.color.yellow,
               mass = 2.0*1000, momentum=vp.vector(0,0,0), make_trail=True)

Теперь нам нужно создать функцию, которая вычисляет силу притяжения:

def gravitationalForce(p1,p2):
	G = 1 #real-world value is : G = 6.67e-11
	rVector = p1.pos - p2.pos
	rMagnitude = vp.mag(rVector)
	rHat = rVector / rMagnitude
	F = - rHat * G * p1.mass * p2.mass /rMagnitude**2
	return F

Чтобы создать анимацию, мы будем использовать метод Эйлера — Кромера, поэтому сначала нам нужно сгенерировать переменную времени и размер шага:

t = 0
dt = 0.0001 #The step size. This should be a small number

В бесконечном цикле мы должны вычислить силу и обновить положение, импульс и переменную времени t следующим образом.

Примечание: мы используем rate(), чтобы ограничить скорость анимации, также можно использовать sleep()

while True:
	vp.rate(500)
  #calculte the force using gravitationalForce function
	star.force = gravitationalForce(star,planet)
	planet.force = gravitationalForce(planet,star)
  #Update momentum, position and time
	star.momentum = star.momentum + star.force*dt
	planet.momentum = planet.momentum + planet.force*dt
	star.pos = star.pos + star.momentum/star.mass*dt
	planet.pos = planet.pos + planet.momentum/planet.mass*dt
	t+= dt

А теперь попробуем добавить больше планет.

Примечание: мы можем использовать RGB для объявления цвета следующим образом:

star = vp.sphere(pos=vp.vector(0,0,0), radius=0.2, color=vp.color.yellow,
               mass = 1000, momentum=vp.vector(0,0,0), make_trail=True)

planet1 = vp.sphere(pos=vp.vector(1,0,0), radius=0.05, color=vp.color.green,
               mass = 1, momentum=vp.vector(0,30,0), make_trail=True)

planet2 = vp.sphere(pos=vp.vector(0,3,0), radius=0.075, color=vp.vector(0.0,0.82,0.33),#RGB color
                  mass = 2, momentum=vp.vector(-35,0,0), make_trail=True)
                  
planet3  = vp.sphere(pos=vp.vector(0,-4,0), radius=0.1, color=vp.vector(0.58,0.153,0.68),
                  mass = 10, momentum=vp.vector(160,0,0), make_trail=True)

Затем обновите позицию и импульс:

while (True):
    vp.rate(500)
    
 	#Calculte the force using gravitationalForce function
    star.force = gravitationalForce(star,planet1)+gravitationalForce(star,planet2)+gravitationalForce(star,planet3)
    planet1.force = gravitationalForce(planet1,star)+gravitationalForce(planet1,planet2)+gravitationalForce(planet1,planet3)
    planet2.force = gravitationalForce(planet2,star)+gravitationalForce(planet2,planet1)+gravitationalForce(planet2,planet3)
    planet3.force = gravitationalForce(planet3,star)+gravitationalForce(planet3,planet1)+gravitationalForce(planet3,planet2)

    #Update momentum, position and time
    star.momentum = star.momentum + star.force*dt
    planet1.momentum = planet1.momentum + planet1.force*dt
    planet2.momentum = planet2.momentum + planet2.force*dt
    planet3.momentum = planet3.momentum + planet3.force*dt

    star.pos = star.pos + star.momentum/star.mass*dt
    planet1.pos = planet1.pos + planet1.momentum/planet1.mass*dt
    planet2.pos = planet2.pos + planet2.momentum/planet2.mass*dt
    planet3.pos = planet3.pos + planet3.momentum/planet3.mass*dt
    
    t += dt

Что у нас получилось:

Заключение

VPython позволяет создавать простые и сложные 3D-анимации для симуляции физических явлений, а также рисовать графики в режиме реального времени.