Симуляция пандемии COVID-19 на Python

Введение

Коронавирус. Пандемия. Самоизоляция. Все эти слова наводняют новостной фон последних недель, и сложно себе представить человека, который ничего не слышал об этой эпидемии. Но насколько всё это страшно и угрожающе? Когда всё это кончится и мы наконец вернёмся к привычной жизни? Многие расходятся во мнениях, пытаясь ответить на эти вопросы. И действительно: прогнозировать ситуацию трудно, особенно, если принять во внимание, что многое зависит от грамотных действий региональных властей. Но, тем не менее, само по себе явление эпидемии подчиняется вполне определённым фундаментальным законам и некоторую схожесть в динамике пандемии мы можем уже сегодня наблюдать в разных странах. Ниже в этой статье я постараюсь построить модель, заложив в неё основные принципы теории распространения вируса, а также произвести компьютерную симуляцию, сопоставив её результаты с тем, что мы наблюдаем в некоторых странах. Данные по ситуации с коронавирусом в мире я брал с официального сайта Johns Hopkins University.

Минутка заботы от НЛО

В мире официально объявлена пандемия COVID-19 — потенциально тяжёлой острой респираторной инфекции, вызываемой коронавирусом SARS-CoV-2 (2019-nCoV). На Хабре много информации по этой теме — всегда помните о том, что она может быть как достоверной/полезной, так и наоборот.

Мы призываем вас критично относиться к любой публикуемой информации

Официальные источники

• Cайт Министерства здравоохранения РФ
• Cайт Роспотребнадзора
• Сайт ВОЗ (англ)
• Сайт ВОЗ
• Сайты и официальные группы оперативных штабов в регионах

Если вы проживаете не в России, обратитесь к аналогичным сайтам вашей страны.

Мойте руки, берегите близких, по возможности оставайтесь дома и работайте удалённо.

Читать публикации про: коронавирус | удалённую работу

Немного теории

С точки зрения распространения вирус характеризуется многими параметрами, вот лишь некоторые из них: инкубационный период, уровень заразности, пути передачи, вероятность бессимптомного протекания, вероятность сценария, при котором больной не обращается к врачу (а значит, не попадает ни в какую статистику), способность к мутациям. С другой стороны, чтобы исследовать феномен эпидемии, необходимо рассматривать ещё и плотность социальных связей между людьми, что напрямую относится к такому важному показателю, как коэффициент заражения. Он представляет из себя усреднённое количество людей, которых заражает заболевший в течение инкубационного периода и периода болезни. Например, для коронавируса этот коэффициент называют 2.4. Хочу также отдельно отметить, что уровень смертности от вируса практически не влияет на ход самой эпидемии, потому что, либо человек выздоравливает, либо умирает — в обоих случаях он выпадает из числа переносчиков и потенциально заражённых. Хотя следует отдельно сказать про то, что если эпидемия начинает носить массовый характер (от 15% всей популяции и более), то появляется феномен коллективного иммунитета, который снижает коэффициент заражения при той же плотности социальных связей по той причине, что индивиды с иммунитетом не могут заразиться повторно; а это в свою очередь тормозит распространение эпидемии.

Как мы уже видим, факторов, влияющих на динамику эпидемии, большое количество. Некоторые из них учитывать непросто. Поэтому ниже в симуляции мы ограничимся лишь следующими из них:

1. инкубационный период,
2. коэффициент распространения.

Сценарий симуляции

В симуляции эпидемии мы базируемся на следующий сценарий:

1. Появляется первый и единственный заражённый, для него запускается инкубационный период.
2. Пока у него не появились симптомы, он ежедневно заряжает других членов общества в случайном количестве в соответствии с распределением Пуассона (коэффициент в котором зависит от коэффициента распространения вируса). Процесс для всех новых заражённых протекает одинаковым образом, стартуя с момента заражения.
3. Когда инкубационный период заканчивается, у заражённого начинается активная стадия болезни, он обращается в мед. помощь и перестаёт заражать других и в этот день пополняет статистику по зафиксированным случаям.
4. В какой-то момент времени (в определённый день симуляции) власти региона включают карантин, что снижает коэффициент заражения.

Инкубационный период — это характеристика воздействия вируса на человеческий организм, а значит он всегда постоянный и не может быть изменён сам по себе или какими-либо карантинными мерами. Для COVID-19 мы рассматриваем случайное значение от 1 до 14 дней.

Величина коэффициента заражения до карантина зависит от густонаселённости региона и от его социальных особенностей. А после введения карантина — от конкретики и эффективности самих мер. Данные значения могут разниться достаточно сильно между странами. Например, для Италии удалось подобрать значения 0.35 до карантина (это количество заражаемых каждым заражённым в день, что приблизительно соответствует значению 2.4 за весь инкубационный период, положив его равным случайному значению от 1 до 14) и 0.135 после. Эти коэффициенты наиболее точно описывают ту динамику эпидемии, что мы сейчас наблюдаем. Но об этом чуть позже.

Код симуляции на Python

Вот и дошли до самого интересного: от теории к практике. Ниже я привожу полный код симуляции, который включает в себя установку необходимых параметров, цикл самой симуляции и построение графиков общего числа зафиксированных случаев (Total cases), ежедневный прирост заболевших (New cases) и интересный параметр количества носителей вируса в обществе (Infected), у которых ещё не проявились симптомы, но именно они являются активными распространителями (этот параметр не может быть напрямую измерен в какой-либо национальной статистике, но даёт хорошее понимание внутренней кухни протекающей эпидемии).

import numpy as np
import matplotlib.pyplot as plt

COUNTRY = "Italy"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 74
INCUBATION_PERIOD = 15

# Для воспроизводимости результатов
np.random.seed(0)

# Здесь логика вычисления коэффициента распространения в зависимости от дня. 
# Реализовал сценарий двух разных коэффициентов: до и после введения карантина. 
# Но ничего не запрещает усложнить функцию, добавив в неё, например, 
# мягкий и жёсткий карантин в разные даты с разными коэффициентами или что-то ещё.
def get_coef(day):
    return COEF_BASE if day < DAY_QUARANTINE else COEF_QUARANTINE

if __name__ == "__main__":
    # Дни симуляции
    days = np.arange(1, DAYS_OF_SIMULATION)

    # Первый инфицированный
    infected = np.random.randint(1, INCUBATION_PERIOD, 1)

    infected_lst = []  # Список хранит в себе дни заражённых, в которые у них проявится болезнь
    new_cases_lst = []
    new_cases_total_lst = []

    # Цикл симуляции по дням
    for day in days:
        # Берём коэффициент распространения
        coef = get_coef(day)

    # Проверяем заражённых на предмет появления симптомов
        new_cases_idx = np.argwhere(infected == day).flatten()

        # Регистрируем заражённых с симптомами как новые случаи заражения
        new_cases_count = new_cases_idx.size

        # Удаляем заражённых с симптомами из списка инфицированных, способных заражать
        infected = np.delete(infected, new_cases_idx)

        # Генерируем новых заражённых в соответствии с распределением Пуассона и добавляем их к имеющимся
        new_infected_count = np.random.poisson(coef, infected.size).sum()
        new_infected = np.random.randint(1, INCUBATION_PERIOD, new_infected_count) + day
        infected = np.concatenate((infected, new_infected))

        # Заполняем статистику
        infected_lst.append(infected.size)
        new_cases_lst.append(new_cases_count)
        new_cases_total_lst.append(sum(new_cases_lst))

        print(day, infected.size)

    plt.figure(figsize=(16, 8))

    # График общего количества заражений
    plt.subplot(311)
    plt.title(f"COVID-19 pandemic in {COUNTRY}")
    plt.plot(days, new_cases_total_lst)
    plt.grid(True)
    plt.legend(["Total cases"], loc='upper left')

    # График новых ежедневных случаев заражения
    plt.subplot(312)
    plt.bar(days, new_cases_lst, alpha=0.7, color='y')
    plt.grid(True)
    plt.legend(["New cases"], loc='upper left')

    # График ежедневного количества инфицированных
    plt.subplot(313)
    plt.plot(days, infected_lst, color='r')
    plt.grid(True)
    plt.legend(["Infected"], loc='upper left')

    plt.show()

Кратко по параметрам.

DAYS_OF_SIMULATION - количество дней в симуляции,
COEF_BASE - коэффициент дневного распространения до введения карантинных мер,
COEF_QUARANTINE - коэффициент дневного распространения после введения карантинных мер,
DAY_QUARANTINE - день введения карантинных мер с момента начала симуляции,
INCUBATION_PERIOD - верхняя грань инкубационного периода в днях (не включительно).

Результаты симуляции для Италии и США

Варьируя параметры, можно получать динамику для разных стран, а также экстраполировать ход эпидемии в будущее и иметь картину о количестве инфицированных в каждый момент времени.

Например, для Италии удалось подобрать параметры:

COUNTRY = "Italy"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 74
INCUBATION_PERIOD = 15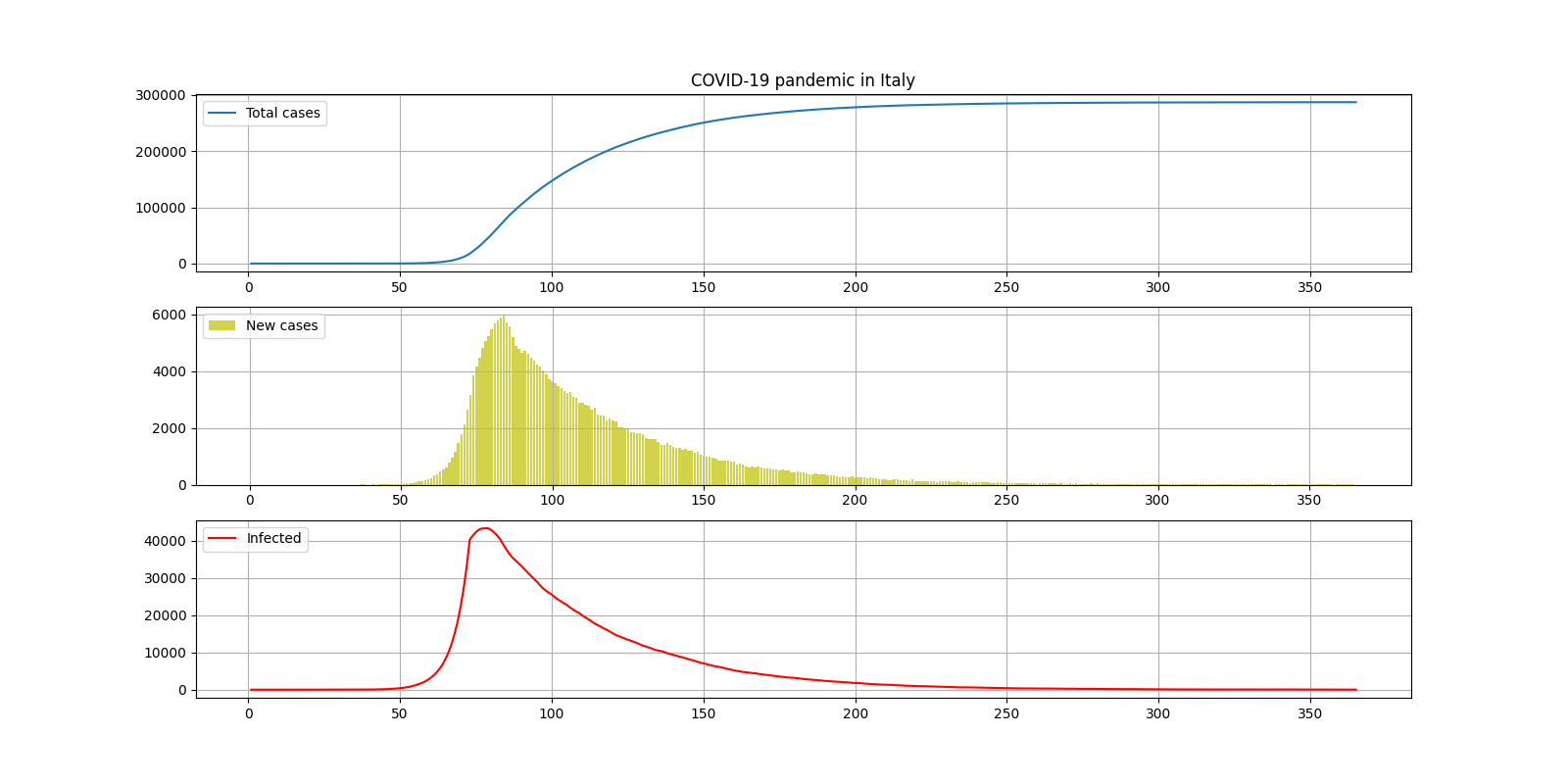

Что неплохо соответствует наблюдаемой картине на сегодняшний день. Такой результат удаётся получить из-за того, что Италия ввела эффективные карантинные меры в определённый момент (на 74-й день с момента первого инфицированного по условиям симуляции), после чего всё равно наблюдается рост числа заражений из-за инкубационного периода, что логично, а ещё через 14 дней заражения и количество инфицированных заметно идут на спад. По графику можно также сделать прогноз, что общее количество зарегистрированных случаев достигнет примерно 300000, а за окончание эпидемии можно взять 250-й день симуляции, что составляет 180 дней с момента введения карантинных мер (а это, на минуточку, 6 месяцев). Также по сценарию симуляции видно, что в пике максимальное количество инфицированных превосходило 40000.

Резюмируем:
Общее количество случаев за всё время — 300000
Окончание — 6 месяцев после введения карантина
Максимальное количество инфицированных — 40000

Для США, как антилидеров в этой мировой эпидемии, удалось подобрать вот такие параметры:

COUNTRY = "USA"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 83
INCUBATION_PERIOD = 15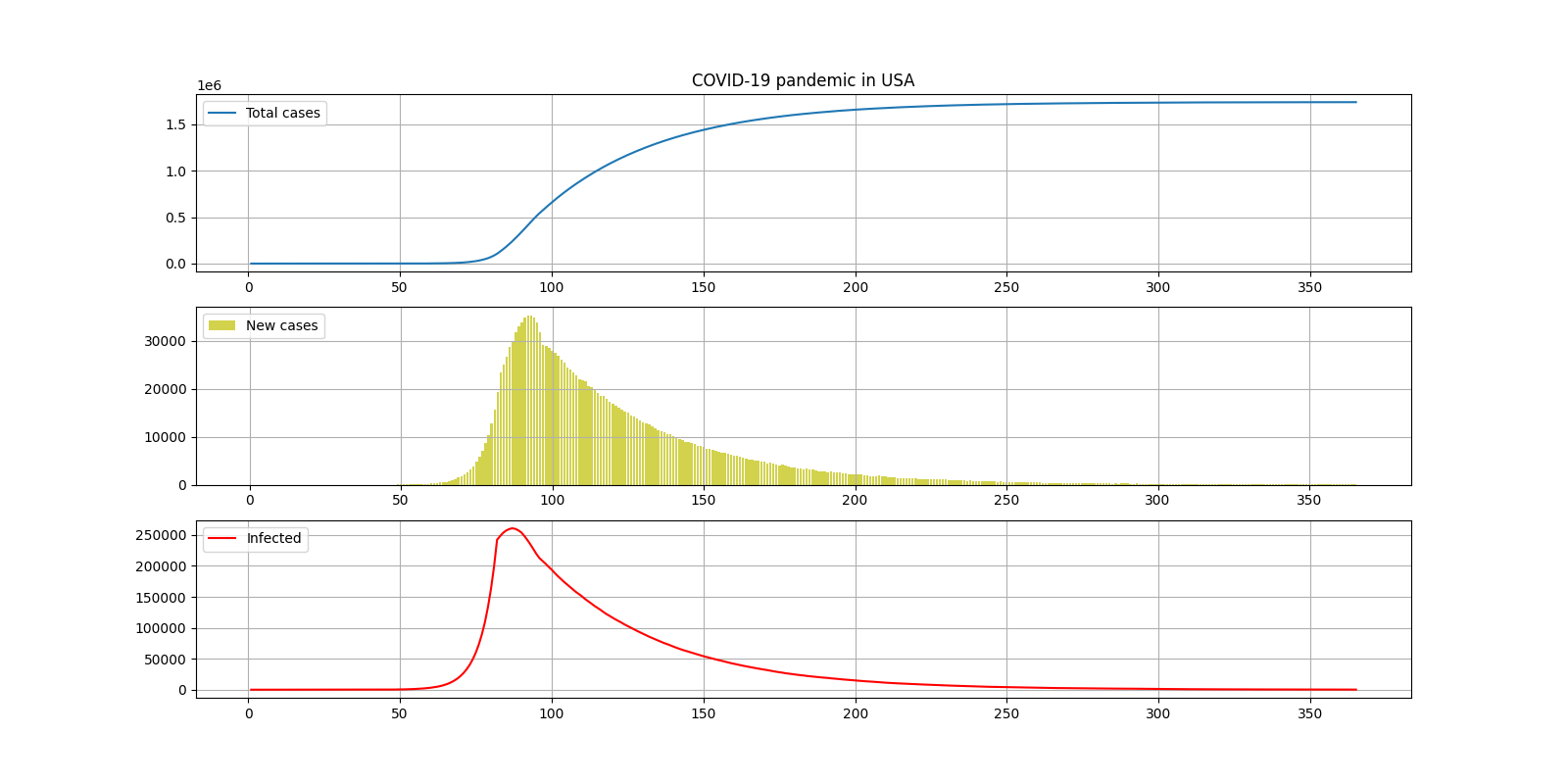

Доверять результатам следует с осторожностью. Потому что, несмотря на то, что страна проходит пик эпидемии (а значит DAY_QUARANTINE установлен более-менее правильно), мы ещё мало что знает об эффективности карантина, а значит параметр COEF_QUARANTINE по большому счёту неизвестен. Я взял его итальянским как первое приближение.

Резюмируем:
Общее количество случаев за всё время — 1700000
Окончание — 6 месяцев после введения карантина
Максимальное количество инфицированных — 250000

Симуляция для России

Хабр — это по большей части российский портал, поэтому Россия является наиболее интересным объектом для симуляции. Но к сожалению на сегодня в графике новых случаев заражения и общего количества кейсов мы видим две ровные экспоненты, что свидетельствует о том, что эффективные карантинные меры у нас не введены. Каждый день промедления с карантином значительно запускает ситуацию и заметно удлиняет период "выздоровления" общества. Поэтому я рассмотрел три сценария:

1. Оптимистичный — карантинные меры начинаю работать сегодня.
2. Пессимистичный 1 — карантинные меры начинают работать через неделю.
3. Пессимистичный 2 — карантинные меры начинают работать через две недели.

Получаем следующие результаты.

I. Оптимистичный

COUNTRY = "Russia"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 73
INCUBATION_PERIOD = 15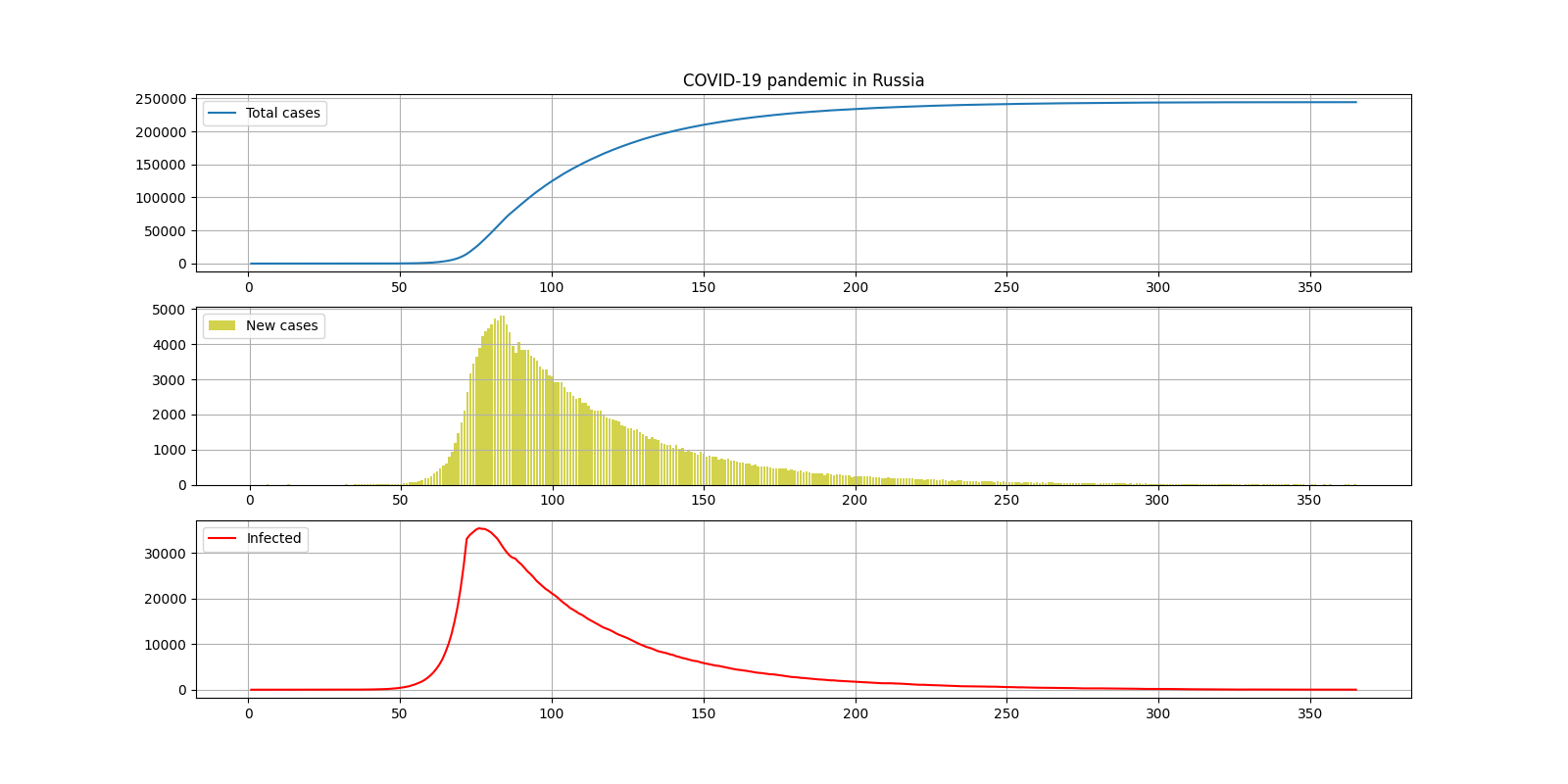

Общее количество случаев за всё время — 250000
Окончание — 6 месяцев после введения карантина
Максимальное количество инфицированных — 35000

II. Пессимистичный 1

COUNTRY = "Russia"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 80
INCUBATION_PERIOD = 15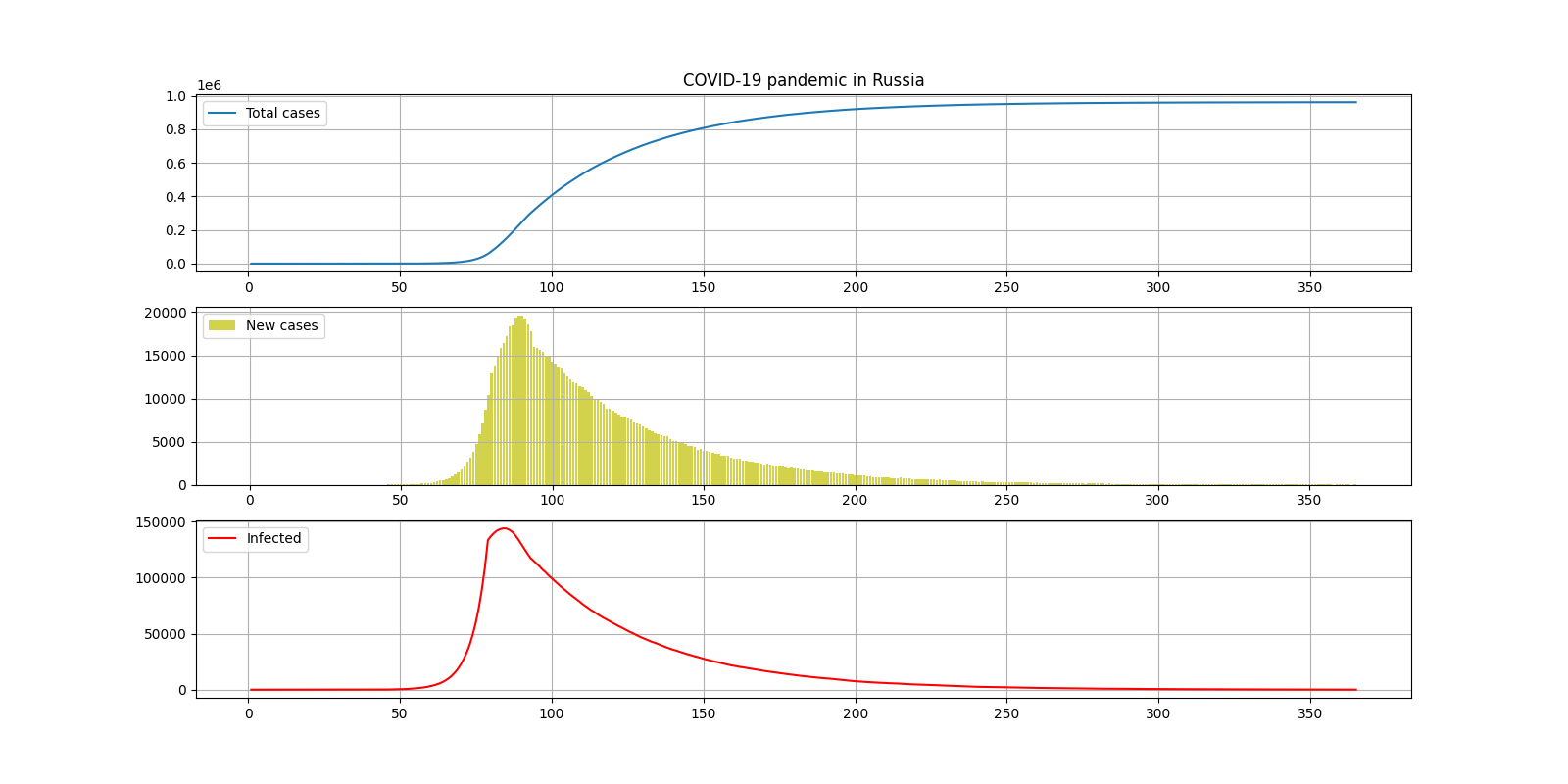

Общее количество случаев за всё время — 950000
Окончание — 7 месяцев после введения карантина
Максимальное количество инфицированных — 140000

III. Пессимистичный 2

COUNTRY = "Russia"
DAYS_OF_SIMULATION = 366
COEF_BASE = 0.35
COEF_QUARANTINE = 0.135
DAY_QUARANTINE = 87
INCUBATION_PERIOD = 15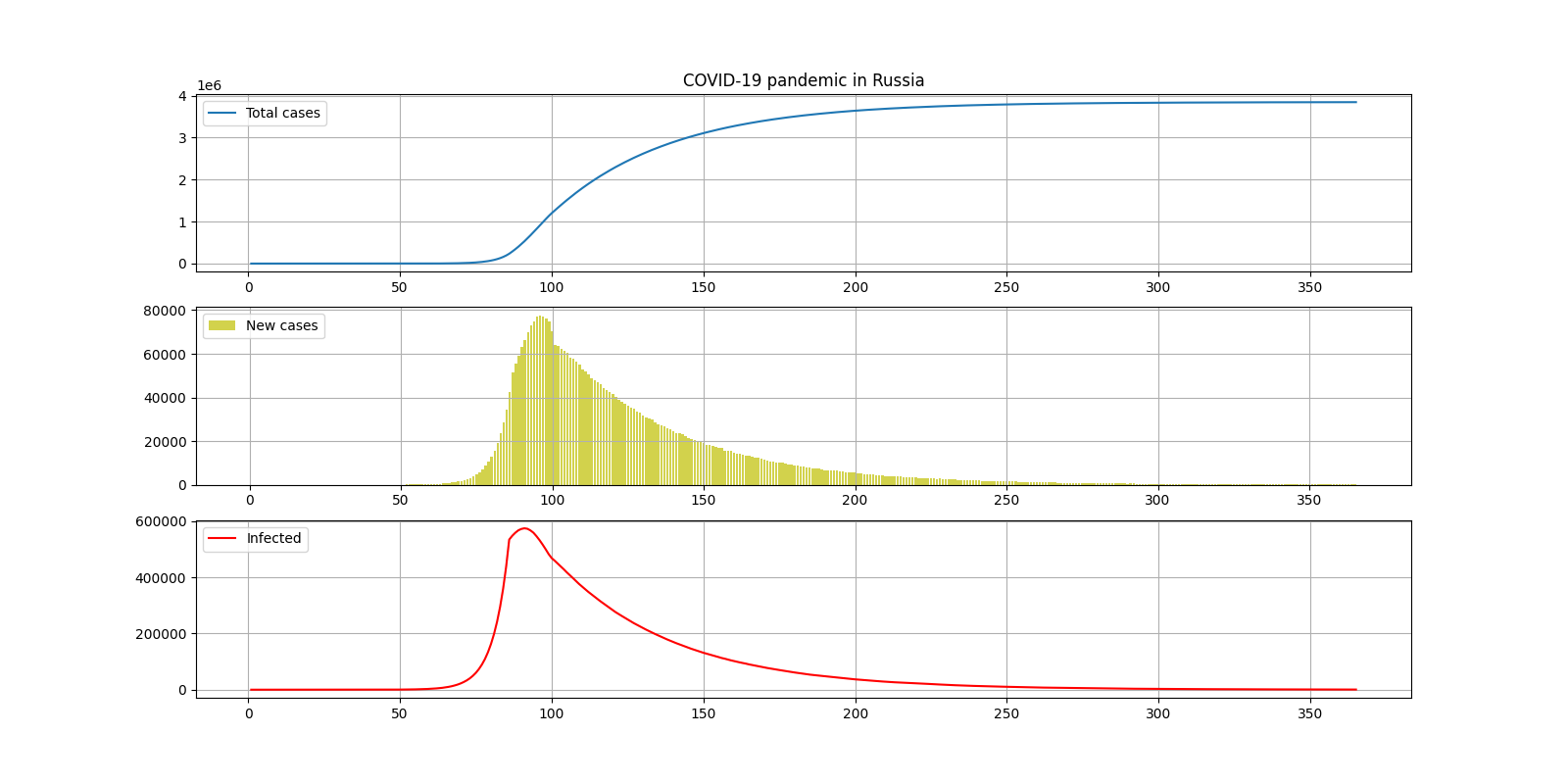

Общее количество случаев за всё время — 4000000
Окончание — 8 месяцев после введения карантина
Максимальное количество инфицированных — 550000

Этим результатам симуляции я особо не стал бы верить, потому что, во-первых, мы не знаем точного времени начала карантина DAY_QUARANTINE, а также коэффициента изоляции после принятия карантинных мер COEF_QUARANTINE, который главным образом зависит от эффективности самих мер (я использовал итальянский коэффициент, хотя далеко не обязательно будет реализован именно он). Но с другой стороны некоторые выводы сделать всё-таки можно уже сегодня:

1. необходимость карантина скорее всего растягивается на месяцы, до осени;
2. каждый день промедления с карантином сильно влияет на общее количество заражений за всё время;
3. многое зависит от эффективности карантинных мер.

Недостатки данного подхода к симуляции

Несмотря на обилие цифр, графики и приведённый алгоритм симуляции, я бы хотел призвать относиться ко всем этим результатам с большой осторожностью. Ведь мы занимаемся задачей экстраполяции, в которой небольшие изменения параметров способны крайне сильно влиять на финальный результат. А также мы воспользовались рядом допущений, которые могут быть критичны на практике. Например:

1. Не рассматриваются случаи, когда заболевшие переносят болезнь дома, никому не сообщая,
2. Не рассматриваются бессимптомные носители,
3. Никак не учитывается коллективный иммунитет (а это существенно, если количество заболевших соизмеримо с величиной популяции),
4. Обратившиеся за помощью автоматически выпадают из потенциальных переносчиков,
5. Не учитываются постепенно вводимые меры карантина,
6. … многое другое.

Я предлагаю читателям поиграться со скриптом, попробовать смоделировать процесс для других стран, отписаться об этом в комментариях. А также интересно усложнить симуляцию, добавив туда больше неучтённых факторов.