Природа использует всевозможные интересные и часто простые процессы для генерации удивительных фигур, паттернов и форм любых размеров, которые никогда не перестают удивлять и вдохновлять внимательного наблюдателя. От микроскопического до космического уровня материя выстраивается, упорядочивается и преобразуется при помощи логичных наблюдаемых процессов, часто накладывающихся друг на друга сложным образом.
В этой статье мы поговорим об одном из таких процессов, называемом агрегацией, ограниченной диффузией (diffusion-limited aggregation, или DLA), создающем фрактальные ветвящиеся структуры при помощи случайного движения и «липких» частиц (подробнее о них позже). Свидетельства этого процесса можно найти в природе в различных масштабах и в органических, и в неорганических системах, например:

Наверху: кластер DLA, выращенный из раствора медного купороса в ячейке для электроосаждения; внизу: коллоидный диоксид кремния с площадью поверхности 130 м2/г


Наверху: наслоение металлической пыли от работы отрезной пилы; внизу: фигура Лихтенберга в куске оргстекла.


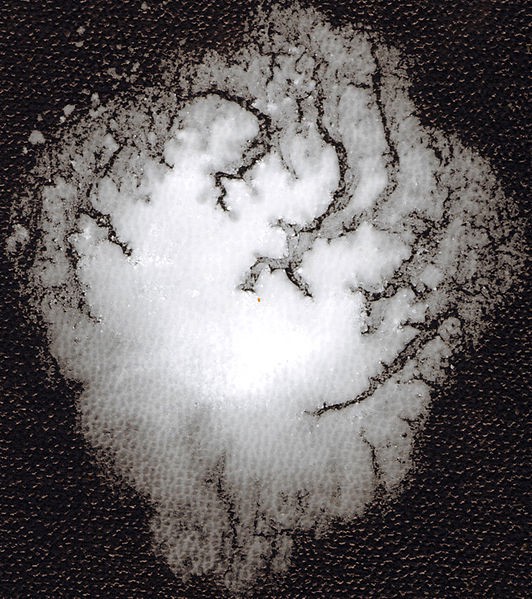
Наверху: пример морозных узоров на стекле; внизу: образец дендритов двуокиси марганца на известняковом осадочном слое из Зольнхофена, Германия.
Агрегация, ограниченная диффузией, впервые описанная Томасом Уиттеном и Леонардом Сэндером в их выдающейся статье 1981 года Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon — это процесс слипания частиц материи (агрегации) при их хаотическом движении (диффузии) в среде, обеспечивающей некую противодействующую (ограничивающую) силу. Со временем такие частицы слипаются, образуя характерные фрактальные ветвящиеся структуры, называемые броуновскими деревьями.
Для иллюстрации процесса представьте, что у вас есть несколько теннисных мячей, покрытых особым волшебным клеем, который приклеивается только к себе, то есть эти мячи крепко соединяются друг с другом, но не прикрепляются к полу, стенам или другим объектам. Положим один мяч на пол небольшой комнаты и начнём случайным образом вбрасывать туда остальные теннисные мячи, не целясь куда-то конкретно.
Рано или поздно некоторые из этих мячей столкнутся или с первым мячом, или с другими вброшенными мячами и начнут образовывать прочные кластеры. При вбрасывании дополнительных мячей эти кластеры растут и создают сложные кустообразные структуры.
Теперь представьте, что мы повторим этот эксперимент в гораздо большем здании, например, на заводском складе, и разбросаем повсюду многие тысячи липких теннисных мячей. Со временем мы увидим, как обретают форму большие кластеры мячей, похожие на показанные выше фотографии!
У Дэна Шифмана есть отличное, более наглядное объяснение процесса:
В природе эти липкие теннисные мячи/случайные блуждатели могут быть ионизированными атомами, поляризованными молекулами, заряженными взвешенными частицами или любым количеством других частиц материи, имеющих склонность ко взаимному слипанию. Если эти частицы будут двигаться хаотичным (или полухаотичным) образом и иметь при этом склонность к слипанию, то благодаря процессу агрегации, ограниченной диффузией, будут возникать узнаваемые фрактальные ветвящиеся структуры!
Чтобы реализовать этот процесс в коде, нам нужно сначала определить основные объекты и силы, которые мы хотим моделировать. Исходя из описанного выше, логично создать некую структуру данных, обозначающую частицу (теннисный мяч), таким образом, чтобы нам легко было перемещать её по экрану и определять столкновения с другими частицами, чтобы их можно было «склеить». И поскольку мы будем иметь дело со множеством частиц, нам понадобится удобный способ их эффективного отслеживания.
Самым грубым способом реализации был бы простой массив объектов «частица», который мы постоянно обходим в цикле, применяем к нему силы, а затем проверяем каждую другую частицу на коллизии. Однако при увеличении масштаба симуляции этот способ сильно влияет на производительность, потому что при росте размеров кластеров увеличиваются затраты на необязательные вычисления.
Лучше будет использовать какую-нибудь структуру данных или пакет, способный отслеживать все частицы и позволяющий эффективно определять близкие частицы, проверяя их коллизии. Существует несколько стандартных пакетов, которые могут полностью или частично помочь в выполнении этих задач (D3.js, Matter.js, Toxiclibs.js и другие), но мне показалось, что все они гораздо сложнее, чем требуется нам на самом деле.
После кратких поисков я наткнулся на очень удобный, надёжный и лёгкий пакет под простым названием collisions, отслеживающий частицы при помощи внутреннего пространственного индекса и обеспечивающий сверхэффективное распознавание коллизий на основании формы частиц.
Чтобы вдохнуть немного жизни в систему, нам также нужно подумать о движении этих частиц и силах, производящих эти движения. Для большинства людей классическим подходом будет движение каждой «неслипшейся» частицы на небольшую случайную величину в каждом цикле, обеспечивающее так называемое броуновское движение. Вполне хватит чего-то простого наподобие
На молекулярном уровне это похоже на тепловые колебания, связанные с температурой системы — чем выше температура, тем быстрее колеблются частицы. В других масштабах такое движение может быть результатом множества взаимодействующих и накладывающихся друг на друга сил — ветра, давления, поверхностного натяжения, гравитации, электромагнитных сил, и так далее.
Это движение не обязано быть совершенно хаотичным; на самом деле, при комбинировании броуновского движения с направленными или вращающими силами могут создаваться очень интересные эффекты, которые мы рассмотрим ниже.
В первой реализации DLA, описанной в 1981 году Т. Уиттеном и Л. Сэндером, частицы ассоциировались с отдельными пикселями экрана, то есть весь процесс происходил в равномерной сетке квадратов. В то время это было совершенно логично, потому что реализация была основана на предыдущих исследованиях в областях математики и физики, в частности, на модели роста Идена, предложенной Мюрреем Иденом в 1961 году. Также к этой тематике относятся клеточные автоматы, решётчатая модель, кристаллография/структура кристаллов/рост кристаллов и теория матриц.
Любопытно, что такая система на основе сеток значительно упрощала распознавание коллизий и устраняла необходимость в пространственном индексе и вообще в системе частиц, потому что каждый пиксель/частицу можно было проверить на коллизии простым изучением состояния 8 ближайших пикселей-соседей. На самом деле этот подход настолько быстр, что и сегодня является одной из самых быстрых техник!
Конечно, мы можем воссоздать эту реализацию сегодня и воспользоваться теми же преимуществами скорости, но она имеет некоторые компромиссы. Во-первых, хотя плотность пикселей современных экранов гораздо выше, чем в 1981 году, они всё равно имеют ограниченное количество пикселей, поэтому симуляция будет ограничена определённым масштабом. Во-вторых, из-за привязки пикселей к сетке при таком подходе всегда будут создаваться изображения с характерным растровым (блочным) внешним видом.
Первый из этих компромиссов можно компенсировать переходом к виртуальной сетке вместо пикселей экрана. Можно создать сетку произвольного, даже динамического размера, которую можно масштабировать, перемещать и поворачивать вне зависимости от размеров экрана, почти как Google Maps. Я бы с удовольствием посмотрел, как кто-нибудь попробует это сделать и поделится результатами!
Однако второй компромисс обойти сложнее. Я хотел увидеть, что процесс DLA может создать при неравномерной и неквадратной форме частиц, поэтому я решил, что для широких возможностей в экспериментах в любом случае придётся отделить частицы от структуры сетки. Однако в таком случае придётся использовать такие инструменты, как пространственное индексирование и более сложное распознавание коллизий, которые неизбежно повлияют на производительность. С моей точки зрения этот компромисс между скоростью и гибкостью эстетики стоил того, по крайней мере, для моей серии исследовательских экспериментов. Кроме того, если я найду понравившийся мне эффект, то всегда смогу потом выполнить рефакторинг кода, чтобы оптимизировать его под этот эффект!
Хватит теории — давайте что-нибудь создадим!
В основе моей реализации лежит p5.js, потому что он полезен своими функциями рисования на
В процессе создания моей реализации я использовал следующие пакеты, доступные через NPM:
Так как я знал, что хочу провести по этой теме несколько экспериментов, то решил отделить мой относящийся к DLA код от эскизов p5.js, чтобы каждый эскиз был связан только с конфигурацией и выполнением процесса DLA, как будто он является сторонним пакетом. Для этого я создал папку
Техническая документация этих модулей и их функций на основе JSDoc находится здесь.
Весь исходный код моих экспериментов выложен на Github:jasonwebb/2d-diffusion-limited-aggregation-experiments.
А поиграться со всеми этими экспериментами в браузере можно здесь:
2D diffusion-limited aggregation (DLA) experiments in JavaScript
Данные команды доступны во всех эскизах:
Давайте сразу создадим эскиз с использованием простейшей возможной конфигурации — набора случайно расположенных «порождающих» частиц и набора случайно расположенных и случайно движущихся блуждающих частиц, имеющих одинаковый размер и форму.
В моей реализации достаточно было использовать стандартную функциональность модуля DLA.js со стандартными функциями блуждания и создания кластеров (



Теперь давайте добавим блуждающим частицам дополнительную силу движения (называемую «отклонением»), чтобы они накапливались интересным, частично прогнозируемым образом.
Эту силу отклонения можно добавить в дополнение к стандартному броуновскому движению, чтобы частицы всё равно имели характерное «случайное» поведение, в то же время двигаясь в каком-то конкретном направлении. Сила может прикладываться вдоль только горизонтальной или вертикальной осей (или обеих), или даже согласно заданной формуле (чтобы посмотреть на это, перейдите к эксперименту 07).
В моей реализации направленное отклонение движения можно добавить изменением значения глобального параметра
Чтобы дать частицам то, с чем они могли бы сталкиваться и скапливаться, я добавил «стенки» из кластерных частиц, передавая строку


Наверху — частицы смещаются вниз; внизу — частицы смещаются к центру (только по X).


Наверху — частицы создаются в центре и имеют отклонение от центра; внизу — частицы создаются по краям и имеют отклонение к центру.
Теперь давайте посмотрим, что произойдёт, если мы будем будем варьировать размеры блуждающих частиц. Будет ли ветвящаяся структура выглядеть иначе, и сформируется ли вообще?
В этом эксперименте я придумал для интересных способа варьирования размеров блуждающих частиц — пропорционально расстоянию от центра и случайно в пределах определённого интервала.
Как выяснилось, характерная фрактальная ветвящаяся структура броуновского дерева сама по себе возникает во всех этих вариациях! Это хорошая иллюстрация «самоподобия» природы фракталов, демонстрирующая, что похожие (иногда одинаковые) структуры могут возникать в разных масштабах.


Наверху: увеличение диаметра частиц в зависимости от расстояния до центра; Внизу: случайное варьирование диаметров частиц
Что произойдёт, если мы немного поиграемся с формой блуждающих частиц? Повлияет на ветвящуюся структуру геометрия частиц?
В моей реализации все частицы по умолчанию являются кругами, потому что я решил, что это наиболее распространённая конфигурация. Однако пакет collisions также позволяет использовать отдельные точки или произвольные многоугольники, задаваемые массивами точек. Мне так и не удалось заставить правильно работать режим отдельных точек, зато многоугольники работают замечательно!
Для создания многоугольных фигур достаточно передать массивы координат модулю
В своих эскизах я решил использовать правильные многоугольники разных размеров и с разной величиной поворота. Так как эти многоугольники обладают радиальной симметрией, для изменения общей формы достаточно изменить количество вершин. Например, три вершины для треугольников, четыре для квадратов, и так далее.
Любопытно, что те же фрактальные ветвящиеся структуры снова возникают, опять-таки демонстрируя «самоподобную» природу фракталов. Можно сделать и ещё одно наблюдение — с уменьшением вершин (а значит, и общего размера), ветвящиеся структуры стремятся стать более «плотными», что вполне логично, ведь простые полигоны при агрегации обычно оставляют бОльшие зазоры.




Наверху: треугольники; второе изображение: квадраты; третье изображение: пятиугольники; внизу: случайное количество сторон, от 3 до 6.
До этого момента я использовал довольно простые начальные условия для выполнения процесса DLA — всего лишь отдельные точки или линии («стенки») точек. Следующим логичным шагом стало добавление произвольной геометрии при помощи внешних файлов SVG.
Для этих экспериментов я реализовал новый модуль (
На этот раз мы получили очень красивые и органично выглядящие результаты, потому что характерные ветвящиеся структуры растут на поверхностях наших фигур естественно и случайно. Мне такие эксперименты начинают казаться по-настоящему интересными!
Во всех предыдущих экспериментах использовались очень простые, схематичные условия, которые помогали в изучении самого фундаментального процесса. Однако теперь, когда мы начали работать с произвольной геометрией, возникают действительно творческие результаты. Вот всего лишь несколько простых примеров, которые мне удалось придумать, но я бы с удовольствием посмотрел, что вы создадите самостоятельно!


Наверху: текст, преобразованный в контуры SVG; внизу: различные многоугольники, сопряжённые друг с другом булевыми операциями

Рост 2D-фигуры, сгенерированной при помощи моего веб-приложения SuperformulaSVG
Проводя эти эксперименты, я захотел получить более прямой контроль над движениями блуждающих частиц, чтобы можно было увеличивать рост в определённых областях. В результате я исследовал некоторые интересные возможности, например:
Мне было бы любопытно посмотреть, какие взаимодействия смогли придумать вы!


Наверху: нажмите и удерживайте кнопку мыши, чтобы создать «чёрную дыру», притягивающую к себе все блуждающие частицы; внизу: режим «хвоста мыши» — блуждающие частицы постоянно создаются вокруг текущей позиции мыши и движутся к центру


Наверху: режим «asteroids» — двигайте треугольный корабль клавишами, удерживайте «пробел» для стрельбы; внизу: режим радиальной «Bust a Move» — нажимайте A и D для вращения, удерживайте кнопку мыши для стрельбы огненными блуждающими частицами в сторону мыши.
Последнее, что я смог придумать — это эксперимент, вдохновлённый Coding Challenge #24: Perlin Noise Flow Field Дэниела Шифмана, в котором для управления движением частиц на экране он использует уравнение. В частности, он использовал популярную функцию noise() Перлина, однако можно взять и множество других уравнений.
В моей реализации достаточно было задать функцию, на входе получающую ссылку на частицу и возвращающую скорость по X и Y (
Здесь можно исследовать очень многое, но должен признаться, что не очень знаком с различными уравнениями полей обтекания. Если вы знаете интересные уравнения, то поделитесь со мной!
30 000 блуждающих частиц, направляемых функцией 2D-шума Перлина
30 000 частиц, направляемых уравнением sin(x) + sin(y)
Во время реализации этих экспериментов я наткнулся на пару интересных визуальных эффектов, которые решил превратить в глобально доступные возможности.
В этом эффекте мы рисуем только линии между каждыми частицами, а не сами частицы. Это создаёт очень органически выглядящие ветвящиеся структуры, которые немного напоминают вены!
Этот эффект можно включить в любом из описанных выше экспериментов, нажав клавишу

Одна из наиболее полезных возможностей — функция экспорта в любой момент времени рисунков SVG нажатием клавиши

Если вы знаете, как обращаться с цветовым кругом (а я, к сожалению, не знаю), то сможете настраивать цвета каждого элемента симуляции, создавая потрясающие эффекты. Зайдите в раздел «COLORS» файла

На самом деле эта статья является просто введением в ограниченную диффузией агрегацию, и в данном разделе представлено множество других способов, которыми можно развить идею.
Если вы хотите глубже исследовать эту тему, то вот несколько статей и репозиториев кода, которые я нашёл в процессе выполнения исследований для этой статьи:
В этой статье мы поговорим об одном из таких процессов, называемом агрегацией, ограниченной диффузией (diffusion-limited aggregation, или DLA), создающем фрактальные ветвящиеся структуры при помощи случайного движения и «липких» частиц (подробнее о них позже). Свидетельства этого процесса можно найти в природе в различных масштабах и в органических, и в неорганических системах, например:


Наверху: кластер DLA, выращенный из раствора медного купороса в ячейке для электроосаждения; внизу: коллоидный диоксид кремния с площадью поверхности 130 м2/г


Наверху: наслоение металлической пыли от работы отрезной пилы; внизу: фигура Лихтенберга в куске оргстекла.


Наверху: пример морозных узоров на стекле; внизу: образец дендритов двуокиси марганца на известняковом осадочном слое из Зольнхофена, Германия.
Что такое агрегация, ограниченная диффузией?
Агрегация, ограниченная диффузией, впервые описанная Томасом Уиттеном и Леонардом Сэндером в их выдающейся статье 1981 года Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon — это процесс слипания частиц материи (агрегации) при их хаотическом движении (диффузии) в среде, обеспечивающей некую противодействующую (ограничивающую) силу. Со временем такие частицы слипаются, образуя характерные фрактальные ветвящиеся структуры, называемые броуновскими деревьями.
Для иллюстрации процесса представьте, что у вас есть несколько теннисных мячей, покрытых особым волшебным клеем, который приклеивается только к себе, то есть эти мячи крепко соединяются друг с другом, но не прикрепляются к полу, стенам или другим объектам. Положим один мяч на пол небольшой комнаты и начнём случайным образом вбрасывать туда остальные теннисные мячи, не целясь куда-то конкретно.
Рано или поздно некоторые из этих мячей столкнутся или с первым мячом, или с другими вброшенными мячами и начнут образовывать прочные кластеры. При вбрасывании дополнительных мячей эти кластеры растут и создают сложные кустообразные структуры.
Теперь представьте, что мы повторим этот эксперимент в гораздо большем здании, например, на заводском складе, и разбросаем повсюду многие тысячи липких теннисных мячей. Со временем мы увидим, как обретают форму большие кластеры мячей, похожие на показанные выше фотографии!
У Дэна Шифмана есть отличное, более наглядное объяснение процесса:
В природе эти липкие теннисные мячи/случайные блуждатели могут быть ионизированными атомами, поляризованными молекулами, заряженными взвешенными частицами или любым количеством других частиц материи, имеющих склонность ко взаимному слипанию. Если эти частицы будут двигаться хаотичным (или полухаотичным) образом и иметь при этом склонность к слипанию, то благодаря процессу агрегации, ограниченной диффузией, будут возникать узнаваемые фрактальные ветвящиеся структуры!
Замечания о технической реализации
Чтобы реализовать этот процесс в коде, нам нужно сначала определить основные объекты и силы, которые мы хотим моделировать. Исходя из описанного выше, логично создать некую структуру данных, обозначающую частицу (теннисный мяч), таким образом, чтобы нам легко было перемещать её по экрану и определять столкновения с другими частицами, чтобы их можно было «склеить». И поскольку мы будем иметь дело со множеством частиц, нам понадобится удобный способ их эффективного отслеживания.
Когда частицы перемещаются свободно, они называются блуждающими (walkers). Когда они слипаются, то вместе их называют кластерами.
Системы частиц, пространственное индексирование и распознавание коллизий
Самым грубым способом реализации был бы простой массив объектов «частица», который мы постоянно обходим в цикле, применяем к нему силы, а затем проверяем каждую другую частицу на коллизии. Однако при увеличении масштаба симуляции этот способ сильно влияет на производительность, потому что при росте размеров кластеров увеличиваются затраты на необязательные вычисления.
Лучше будет использовать какую-нибудь структуру данных или пакет, способный отслеживать все частицы и позволяющий эффективно определять близкие частицы, проверяя их коллизии. Существует несколько стандартных пакетов, которые могут полностью или частично помочь в выполнении этих задач (D3.js, Matter.js, Toxiclibs.js и другие), но мне показалось, что все они гораздо сложнее, чем требуется нам на самом деле.
После кратких поисков я наткнулся на очень удобный, надёжный и лёгкий пакет под простым названием collisions, отслеживающий частицы при помощи внутреннего пространственного индекса и обеспечивающий сверхэффективное распознавание коллизий на основании формы частиц.
Движение
Чтобы вдохнуть немного жизни в систему, нам также нужно подумать о движении этих частиц и силах, производящих эти движения. Для большинства людей классическим подходом будет движение каждой «неслипшейся» частицы на небольшую случайную величину в каждом цикле, обеспечивающее так называемое броуновское движение. Вполне хватит чего-то простого наподобие
particle.x|y += Math.random(-1,1).На молекулярном уровне это похоже на тепловые колебания, связанные с температурой системы — чем выше температура, тем быстрее колеблются частицы. В других масштабах такое движение может быть результатом множества взаимодействующих и накладывающихся друг на друга сил — ветра, давления, поверхностного натяжения, гравитации, электромагнитных сил, и так далее.
Это движение не обязано быть совершенно хаотичным; на самом деле, при комбинировании броуновского движения с направленными или вращающими силами могут создаваться очень интересные эффекты, которые мы рассмотрим ниже.
Сетки — использовать или нет?
В первой реализации DLA, описанной в 1981 году Т. Уиттеном и Л. Сэндером, частицы ассоциировались с отдельными пикселями экрана, то есть весь процесс происходил в равномерной сетке квадратов. В то время это было совершенно логично, потому что реализация была основана на предыдущих исследованиях в областях математики и физики, в частности, на модели роста Идена, предложенной Мюрреем Иденом в 1961 году. Также к этой тематике относятся клеточные автоматы, решётчатая модель, кристаллография/структура кристаллов/рост кристаллов и теория матриц.
Любопытно, что такая система на основе сеток значительно упрощала распознавание коллизий и устраняла необходимость в пространственном индексе и вообще в системе частиц, потому что каждый пиксель/частицу можно было проверить на коллизии простым изучением состояния 8 ближайших пикселей-соседей. На самом деле этот подход настолько быстр, что и сегодня является одной из самых быстрых техник!
Конечно, мы можем воссоздать эту реализацию сегодня и воспользоваться теми же преимуществами скорости, но она имеет некоторые компромиссы. Во-первых, хотя плотность пикселей современных экранов гораздо выше, чем в 1981 году, они всё равно имеют ограниченное количество пикселей, поэтому симуляция будет ограничена определённым масштабом. Во-вторых, из-за привязки пикселей к сетке при таком подходе всегда будут создаваться изображения с характерным растровым (блочным) внешним видом.
Первый из этих компромиссов можно компенсировать переходом к виртуальной сетке вместо пикселей экрана. Можно создать сетку произвольного, даже динамического размера, которую можно масштабировать, перемещать и поворачивать вне зависимости от размеров экрана, почти как Google Maps. Я бы с удовольствием посмотрел, как кто-нибудь попробует это сделать и поделится результатами!
Однако второй компромисс обойти сложнее. Я хотел увидеть, что процесс DLA может создать при неравномерной и неквадратной форме частиц, поэтому я решил, что для широких возможностей в экспериментах в любом случае придётся отделить частицы от структуры сетки. Однако в таком случае придётся использовать такие инструменты, как пространственное индексирование и более сложное распознавание коллизий, которые неизбежно повлияют на производительность. С моей точки зрения этот компромисс между скоростью и гибкостью эстетики стоил того, по крайней мере, для моей серии исследовательских экспериментов. Кроме того, если я найду понравившийся мне эффект, то всегда смогу потом выполнить рефакторинг кода, чтобы оптимизировать его под этот эффект!
Подготовка проекта
Хватит теории — давайте что-нибудь создадим!
В основе моей реализации лежит p5.js, потому что он полезен своими функциями рисования на
<canvas>, а также JavaScript в стиле ES6, транспилированный на ES5 под браузеры текущего поколения при помощи скриптов Webpack и NPM. Подробнее см. в файлах webpack.config.js и package.json.В процессе создания моей реализации я использовал следующие пакеты, доступные через NPM:
- collisions для надёжного и лёгкого распознавания коллизий без использования пакета полной физики. В этот пакет входит иерархия ограничивающих объёмов (bounding volume hierarchy) (BVH), используемая для пространственного индексирования.
- svg-pathdata для парсинга информации контуров из файлов SVG, позволяющего создавать собственные формы.
- svg-points для генерации атрибута
dSVG-элементов<path>для экспорта векторных изображений. - file-saver для инициализации скачивания экспортированных файлов SVG на машину пользователя.
Так как я знал, что хочу провести по этой теме несколько экспериментов, то решил отделить мой относящийся к DLA код от эскизов p5.js, чтобы каждый эскиз был связан только с конфигурацией и выполнением процесса DLA, как будто он является сторонним пакетом. Для этого я создал папку
./core со следующими модулями:DLA.js— управляет самой симуляцией и выполняет её. Вызывает функциюiterate()для шага вперёд на один цикл и функциюdraw()для отрисовки всех частиц на экране. Также раскрыта целая куча других функций, что позволяет создавать всевозможные интересные конфигурации!Defaults.js— объект, содержащий в себе параметры конфигурации, которые могут переопределяться отдельными эскизами.
Техническая документация этих модулей и их функций на основе JSDoc находится здесь.
Весь исходный код моих экспериментов выложен на Github:jasonwebb/2d-diffusion-limited-aggregation-experiments.
А поиграться со всеми этими экспериментами в браузере можно здесь:
2D diffusion-limited aggregation (DLA) experiments in JavaScript
Глобальные клавиатурные команды
Данные команды доступны во всех эскизах:
Space— приостановка/продолжение симуляцииw— переключение видимости блуждающих частицc— переключение видимости частиц в кластерахr— сброс симуляции с текущими параметрамиf— переключение отображения «рамки»l— переключение эффекта рендеринга линийe— экспорт в файл SVG того, что в данный момент находится на экране1–9— переключение между вариациями, если они есть
Эксперимент 01 — простая DLA
Давайте сразу создадим эскиз с использованием простейшей возможной конфигурации — набора случайно расположенных «порождающих» частиц и набора случайно расположенных и случайно движущихся блуждающих частиц, имеющих одинаковый размер и форму.
В моей реализации достаточно было использовать стандартную функциональность модуля DLA.js со стандартными функциями блуждания и создания кластеров (
createDefaultWalkers() и createDefaultClusters()).- Посмотреть исходный код этого эксперимента
- Поиграться с экспериментом в браузере



Эксперимент 02 — отклонение направления
Теперь давайте добавим блуждающим частицам дополнительную силу движения (называемую «отклонением»), чтобы они накапливались интересным, частично прогнозируемым образом.
Эту силу отклонения можно добавить в дополнение к стандартному броуновскому движению, чтобы частицы всё равно имели характерное «случайное» поведение, в то же время двигаясь в каком-то конкретном направлении. Сила может прикладываться вдоль только горизонтальной или вертикальной осей (или обеих), или даже согласно заданной формуле (чтобы посмотреть на это, перейдите к эксперименту 07).
В моей реализации направленное отклонение движения можно добавить изменением значения глобального параметра
BiasTowards (или в Defaults.js, или в локальном файле Settings.js) на строку, описывающую направление движения, в котором должжны перемещаться частицы. Можно использовать для BiasTowards следующие значения 'Left', 'Right', 'Up', 'Down', 'Center', 'Edges', 'Equator' и 'Meridian'.Чтобы дать частицам то, с чем они могли бы сталкиваться и скапливаться, я добавил «стенки» из кластерных частиц, передавая строку
'Wall' во время создания новых кластеров при помощи createDefaultClusters(). Когда этот параметр задан, линия из кластерных частиц будет создана на стене (или стенах), противоположных направлению, заданному в BiasTowards. Например, если BiasTowards имеет значение 'Left', то createDefaultClusters('Wall') будет создавать линию из кластерных частиц вдоль правой стены.- Просмотреть исходный код этого эксперимента
- Поиграться с экспериментом в браузере


Наверху — частицы смещаются вниз; внизу — частицы смещаются к центру (только по X).


Наверху — частицы создаются в центре и имеют отклонение от центра; внизу — частицы создаются по краям и имеют отклонение к центру.
Эксперимент 03 — разные размеры
Теперь давайте посмотрим, что произойдёт, если мы будем будем варьировать размеры блуждающих частиц. Будет ли ветвящаяся структура выглядеть иначе, и сформируется ли вообще?
В этом эксперименте я придумал для интересных способа варьирования размеров блуждающих частиц — пропорционально расстоянию от центра и случайно в пределах определённого интервала.
Чтобы включить эти эффекты в моём коде, задайте для илиVaryDiameterByDistance, или дляVaryDiameterRandomlyзначениеtrue. Чтобы оба этих эффекта работали правильно, нужно также указать верхний и нижний предел диаметров частиц, передав массив из двух значений[lower, upper]в параметреCircleDiameterRange. Как это делается, можно посмотреть в файлеSettings.jsэтого эскиза.
Как выяснилось, характерная фрактальная ветвящаяся структура броуновского дерева сама по себе возникает во всех этих вариациях! Это хорошая иллюстрация «самоподобия» природы фракталов, демонстрирующая, что похожие (иногда одинаковые) структуры могут возникать в разных масштабах.
- Посмотреть код этого эксперимента
- Поиграться с экспериментом в браузере


Наверху: увеличение диаметра частиц в зависимости от расстояния до центра; Внизу: случайное варьирование диаметров частиц
Эксперимент 04 — различные формы
Что произойдёт, если мы немного поиграемся с формой блуждающих частиц? Повлияет на ветвящуюся структуру геометрия частиц?
В моей реализации все частицы по умолчанию являются кругами, потому что я решил, что это наиболее распространённая конфигурация. Однако пакет collisions также позволяет использовать отдельные точки или произвольные многоугольники, задаваемые массивами точек. Мне так и не удалось заставить правильно работать режим отдельных точек, зато многоугольники работают замечательно!
Уверен, что если бы мне удалось заставить симуляцию работать через пакет collisions с отдельными точками, то повышение производительности оказалось бы значительным. Пакет использует для разных фигур разные алгоритмы распознавания коллизий, поэтому я не удивился бы, если бы он использовать сетку с «подсчётом соседей», почти как в работе 1981 года Т. Уиттена и Л. Сэндера!
Для создания многоугольных фигур достаточно передать массивы координат модулю
createWalker() алгоритма DLA. У формы этих фигур не так много ограничений, однако в документации к пакету collisions упоминается, что он не поддерживает вогнутые многоугольники (многоугольники с «вмятинами»).В своих эскизах я решил использовать правильные многоугольники разных размеров и с разной величиной поворота. Так как эти многоугольники обладают радиальной симметрией, для изменения общей формы достаточно изменить количество вершин. Например, три вершины для треугольников, четыре для квадратов, и так далее.
Любопытно, что те же фрактальные ветвящиеся структуры снова возникают, опять-таки демонстрируя «самоподобную» природу фракталов. Можно сделать и ещё одно наблюдение — с уменьшением вершин (а значит, и общего размера), ветвящиеся структуры стремятся стать более «плотными», что вполне логично, ведь простые полигоны при агрегации обычно оставляют бОльшие зазоры.
- Посмотреть исходный код эксперимента
- Поиграться с экспериментом в браузере




Наверху: треугольники; второе изображение: квадраты; третье изображение: пятиугольники; внизу: случайное количество сторон, от 3 до 6.
Эксперимент 05 — SVG как начальные данные
До этого момента я использовал довольно простые начальные условия для выполнения процесса DLA — всего лишь отдельные точки или линии («стенки») точек. Следующим логичным шагом стало добавление произвольной геометрии при помощи внешних файлов SVG.
Для этих экспериментов я реализовал новый модуль (
SVGLoader.js), считывающий очень простые файлы SVG и возвращающий массивы координат каждого контура (<path>), которые можно использовать для построения многоугольников непосредственно через пакет распознавания коллизий. После чего коллизии блуждающих частиц нужно проверять и с кластерными частицами, и с этими нарисованными фигурами.Чтобы упростить свою жизнь, я сделал так, что модуль SVGLoader может принимать только определённые файлы SVG. Если вы захотите использовать собственные файлы SVG, то они должны отвечать следующим критериям:
1. Формат файла должен быть как можно более простым. В Inkscape нужно сохранять файл как «plain SVG». Возможно, придётся открыть файл SVG и немного его упростить. Для понимания взгляните на содержимое файлов в папке./svg.
2. Все координаты должны быть абсолютными.
3. Принимаются только прямые линии — никаких дуг, окружностей, кривых и т.д. Можно аппроксимировать кривые, добавив множество дополнительных узлов и преобразовав их в прямые сегменты.
На этот раз мы получили очень красивые и органично выглядящие результаты, потому что характерные ветвящиеся структуры растут на поверхностях наших фигур естественно и случайно. Мне такие эксперименты начинают казаться по-настоящему интересными!
Во всех предыдущих экспериментах использовались очень простые, схематичные условия, которые помогали в изучении самого фундаментального процесса. Однако теперь, когда мы начали работать с произвольной геометрией, возникают действительно творческие результаты. Вот всего лишь несколько простых примеров, которые мне удалось придумать, но я бы с удовольствием посмотрел, что вы создадите самостоятельно!
- Посмотреть исходный код эксперимента
- Поиграться с экспериментом в браузере


Наверху: текст, преобразованный в контуры SVG; внизу: различные многоугольники, сопряжённые друг с другом булевыми операциями

Рост 2D-фигуры, сгенерированной при помощи моего веб-приложения SuperformulaSVG
Эксперимент 06 — интерактивность
Проводя эти эксперименты, я захотел получить более прямой контроль над движениями блуждающих частиц, чтобы можно было увеличивать рост в определённых областях. В результате я исследовал некоторые интересные возможности, например:
- Эффект «гравитационного колодца», притягивающий блуждающие частицы к позиции мыши при нажатии и удерживании кнопки.
- Эффект «хвоста мыши», непрерывно испускающий блуждающие частицы вокруг курсора мыши, которые имеют отклонение к центру.
- Версия классической игры «Asteroids», в которой игроки могут нажимать WASD для перемещения и Space для стрельбы.
- Радиальная версия классической игры «Bust-a-Move», в которой игроки могут двигаться клавишами A и D, прицеливаться мышью и стрелять её левой кнопкой.
Мне было бы любопытно посмотреть, какие взаимодействия смогли придумать вы!
- Посмотреть исходный код эксперимента
- Поиграться с экспериментом в браузере


Наверху: нажмите и удерживайте кнопку мыши, чтобы создать «чёрную дыру», притягивающую к себе все блуждающие частицы; внизу: режим «хвоста мыши» — блуждающие частицы постоянно создаются вокруг текущей позиции мыши и движутся к центру


Наверху: режим «asteroids» — двигайте треугольный корабль клавишами, удерживайте «пробел» для стрельбы; внизу: режим радиальной «Bust a Move» — нажимайте A и D для вращения, удерживайте кнопку мыши для стрельбы огненными блуждающими частицами в сторону мыши.
Эксперимент 07 — поля обтекания
Последнее, что я смог придумать — это эксперимент, вдохновлённый Coding Challenge #24: Perlin Noise Flow Field Дэниела Шифмана, в котором для управления движением частиц на экране он использует уравнение. В частности, он использовал популярную функцию noise() Перлина, однако можно взять и множество других уравнений.
В моей реализации достаточно было задать функцию, на входе получающую ссылку на частицу и возвращающую скорость по X и Y (
dx и dy), которая затем прибавляется к позиции частицы в базовой функции движения блуждающей частицы (iterate в DLA.js). Мы передаём эту функцию в модуль DLA, присвоив её переменной DLA.customMovementFunction.Здесь можно исследовать очень многое, но должен признаться, что не очень знаком с различными уравнениями полей обтекания. Если вы знаете интересные уравнения, то поделитесь со мной!
- Посмотреть исходный код эксперимента
- Поиграться с экспериментом в браузере
30 000 блуждающих частиц, направляемых функцией 2D-шума Перлина
30 000 частиц, направляемых уравнением sin(x) + sin(y)
Эффекты и возможности
Во время реализации этих экспериментов я наткнулся на пару интересных визуальных эффектов, которые решил превратить в глобально доступные возможности.
Эффект рендеринга линий
В этом эффекте мы рисуем только линии между каждыми частицами, а не сами частицы. Это создаёт очень органически выглядящие ветвящиеся структуры, которые немного напоминают вены!
Этот эффект можно включить в любом из описанных выше экспериментов, нажав клавишу
L.
Экспорт в SVG
Одна из наиболее полезных возможностей — функция экспорта в любой момент времени рисунков SVG нажатием клавиши
e. Эти файлы отлично подходят для производства цифрового контента и могут быть полезными для плоттеров, лазерных резаков, станков с ЧПУ и многих других устройств.
Цвета
Если вы знаете, как обращаться с цветовым кругом (а я, к сожалению, не знаю), то сможете настраивать цвета каждого элемента симуляции, создавая потрясающие эффекты. Зайдите в раздел «COLORS» файла
Defaults.js, чтобы посмотреть, что можно изменять!
Дальнейшее развитие
На самом деле эта статья является просто введением в ограниченную диффузией агрегацию, и в данном разделе представлено множество других способов, которыми можно развить идею.
- Повысить количество частиц до 1-10 миллионов и выше, чтобы понаблюдать за возникновением интересных макроструктур (для вдохновения см. серию Aggregation Энди Ломаса). Возможно, вам удастся пойти ещё дальше и достичь в своих исследованиях нового уровня!
- Чтобы достичь высокого количества частиц, нужно будет использовать более производительный язык или фреймворк: Processing, openFrameworks, Cinder, vanilla C++, Go или Python. Стоит также попробовать профессиональные VFX-инструменты и игровые движки типа Houdini, Unity и Unreal!
- Реализовать более эффективный алгоритм, например, dlaf Майкла Фоглмена.
- Поэкспериментировать с Vision of Chaos сайта Softology.
- Развернуть симуляцию в третье измерение при помощи OpenGL
- Реализовать вероятностный коэффициент «липкости», чтобы варьировать плотность ветвящихся структур. Эта тема хорошо рассмотрена в статье про DLA Пола Бурка.
Ресурсы
Если вы хотите глубже исследовать эту тему, то вот несколько статей и репозиториев кода, которые я нашёл в процессе выполнения исследований для этой статьи:
Статьи
- Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon (1981 год) Томаса Уиттена и Леонарда Сэндера. Статья, с которой всё началось!
Примечание: зайдите в местную общественную или университетскую библиотеку и спросите библиотекаря, может ли он дать бесплатный доступ! - Diffusion-limited aggregation: A kinetic critical phenomenon? (2000 год) Леонарда Сэндера. Дополнение к оригинальной статье.
- DLA — Diffusion Limited Aggregation Пола Бурка
- Diffusion-limited aggregation в Википедии
- Diffusion-Limited Aggregation с сайта Softology
Код
- Coding Challenge #34: Diffusion-Limited Aggregation Дэна Шифмана (репозиторий на Github)
- Coding Challenge #127: Brownian Tree Snowflake Дэна Шифмана (репозиторий на Github)
- simutils-0001: Diffusion limited aggregation Карстен Шмидт (toxiclibs)
- Diffusion Limited Aggregation (PDF) Андре Офринга
- Simulate: Diffusion-Limited Aggregation из примеров в книге FORM+CODE
- Dendron — эскиз на Processing Голана Левина





