Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
С месяц назад начал учить Python по книге Доусона и очнулся уже глубоко в процессе написания своей игры под pygame. ТЗ было таково, что наиболее перспективным показалось сделать игру с псевдо-трехмерной графикой, запихнув в спрайты сохраненные поверхности 3d-сплайнов. О последних и напишу.
Итак, имеются полигоны (проще всего работать с четырехугольниками), на которые мы хотим натянуть кубические поверхности так, чтобы они стыковались достаточно плавно — эти поверхности и есть сплайны.

Удобнее всего сплайн для одного полигона представить в виде функции
Здесь
— кубические многочлены, удовлетворяющие каким-то граничным условиям (на рисунке ниже — салатовые и рыжие кривые, а производные-начальные условия — сиреневые и голубые вектора); u и v меняются в пределах от 0 до 1.

В такой интерпретации теряются некоторые степени (произведения 2-х и 3-х степеней параметров), зато коэффициенты многочлена можно найти, задав всего 12 векторов начальных условий (4 точки полигона и вектора производных по u и по v для каждой точки). На стыках сплайны совпадают, если задаются аналогичные начальные условия для соседних полигонов (вектора производных должны быть коллинеарны, поверхность проходит через те же точки полигона).
Одна беда — производная при такой постановке задачи на всей границе может не совпадать — будут небольшие артефакты на стыках. Можно выдумать еще 4 условия для исправления этого и аккуратно добавить в формулу еще один член
который не испортит границы, но это тема для отдельной статьи.
Альтернативный вариант — Поверхность Безье, но в нем предлагается задавать 16 параметров непонятного (мне) математического смысла, т.е. предполагается, что будет работать своими руками художник. Мне это не очень подходит, поэтому далее следует велосипед с костылями.
Коэффициенты (1) проще всего вычислить, найдя обратную матрицу к матрице значений и производных в углах и помножив на входные условия (три раза, для каждой координаты). Матрица может быть такой:
NumPy отлично с этой задачей справляется.
Остался один вопрос — откуда взять векторы производных. Предполагается, что надо их как-то выбирать исходя из положения соседних (для полигона) точек и из соображения гладкости.
Лично для меня еще было совершенно контринтуитивно, как быть с длиной вектора производной. Направление — понятно, а вот длина?
В итоге родился такой алгоритм:
1. На первом этапе происходит некоторая классификация точек. В графе (который задают точки полигонов и их связи) ищутся и запоминаются циклы длиной 4, а кроме того записываются соседи, наиболее подходящие на роль продолжения ребра полигона (заранее определяется, какие ребра соответствуют изменению параметра u, а какие — v). Вот кусок кода, который ищет, сортирует и запоминает соседей для 0-й точки какого-то цикла:
Дальше, при построении сплайна, производная вдоль ребра (например по параметру u) в точке полигона выбирается исходя из расположения двух точек ребра и одной соседней точки (пусть это будут точки vec1, vec2 и vec3; точка в которой ищется производная — вторая).
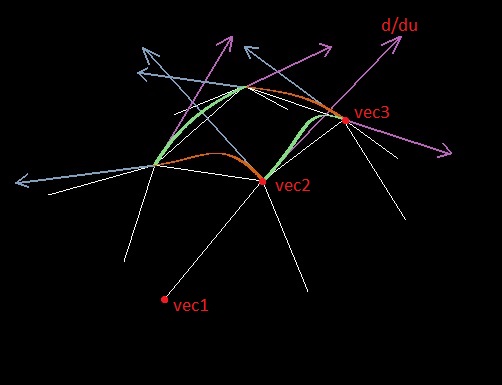
Сначала я пытался использовать для этой роли нормированный вектор vec3 — vec1 (типа применил теорему Лагранжа), но проблемы возникли именно с длиной вектора производных — делать его константой было плохой идеей.
Лирическое отступление:
Для небольшой иллюстрации, что такое вектор производной в параметрическом варианте, обратимся к простой двумерной аналогии — вот кусок дуги окружности:
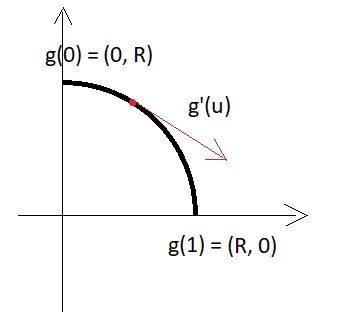
Т.е. модуль производной = R*pi/2 и, вообще говоря, зависит от размера куска дуги, который мы задали через параметр.
Что же с этим теперь делать? Лев Николаевич Толстой завещал нам, что все круглое = хорошее, поэтому, если мы зададим производную в точке так, как если бы хотели построить там дугу, — у нас получится гладкая красивая кривая.
Конец лирического отступления.
Второй этап поиска производной:
2. Через наши три точки vec1, vec2, vec3 строим плоскость, в этой плоскости ищем окружность, которая проходит через все три точки. Искомая производная будет направлена по касательной к окружности в точке vec2, а модуль вектора производной должен равняться произведению радиуса окружности и угла сектора, который образуют две точки грани полигона (аналогично нашей простой плоской аналогии из лирического отступления).
Вроде все просто, вот код функции, например (опять используется NumPy):
Ну и в общем, это все как-то работает. Для демонстрации я взял куб 5х5х5 и менял положение точек рандомайзером:
Итак, имеются полигоны (проще всего работать с четырехугольниками), на которые мы хотим натянуть кубические поверхности так, чтобы они стыковались достаточно плавно — эти поверхности и есть сплайны.

Удобнее всего сплайн для одного полигона представить в виде функции
Здесь
— кубические многочлены, удовлетворяющие каким-то граничным условиям (на рисунке ниже — салатовые и рыжие кривые, а производные-начальные условия — сиреневые и голубые вектора); u и v меняются в пределах от 0 до 1.

В такой интерпретации теряются некоторые степени (произведения 2-х и 3-х степеней параметров), зато коэффициенты многочлена можно найти, задав всего 12 векторов начальных условий (4 точки полигона и вектора производных по u и по v для каждой точки). На стыках сплайны совпадают, если задаются аналогичные начальные условия для соседних полигонов (вектора производных должны быть коллинеарны, поверхность проходит через те же точки полигона).
Одна беда — производная при такой постановке задачи на всей границе может не совпадать — будут небольшие артефакты на стыках. Можно выдумать еще 4 условия для исправления этого и аккуратно добавить в формулу еще один член
который не испортит границы, но это тема для отдельной статьи.
Альтернативный вариант — Поверхность Безье, но в нем предлагается задавать 16 параметров непонятного (мне) математического смысла, т.е. предполагается, что будет работать своими руками художник. Мне это не очень подходит, поэтому далее следует велосипед с костылями.
Коэффициенты (1) проще всего вычислить, найдя обратную матрицу к матрице значений и производных в углах и помножив на входные условия (три раза, для каждой координаты). Матрица может быть такой:
Скрытый текст
[[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], #g(0,0)
[1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0], #g(1,0)
[1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0], #g(0,1)
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], #g(1,1)
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], #dg/du(0,0)
[0, 0, 0, 0, 1, 0, 0, 0, 2, 0, 3, 0], #dg/du(1,0)
[0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0], #dg/du(0,1)
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3], #dg/du(1,1)
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], #dg/dv(0,0)
[0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1], #dg/dv(1,0)
[0, 1, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0], #dg/dv(0,1)
[0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 0, 1]] #dg/dv(1,1)
[1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0], #g(1,0)
[1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0], #g(0,1)
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], #g(1,1)
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0], #dg/du(0,0)
[0, 0, 0, 0, 1, 0, 0, 0, 2, 0, 3, 0], #dg/du(1,0)
[0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0], #dg/du(0,1)
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3], #dg/du(1,1)
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], #dg/dv(0,0)
[0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1], #dg/dv(1,0)
[0, 1, 2, 3, 0, 0, 0, 0, 0, 0, 0, 0], #dg/dv(0,1)
[0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 0, 1]] #dg/dv(1,1)
NumPy отлично с этой задачей справляется.
Остался один вопрос — откуда взять векторы производных. Предполагается, что надо их как-то выбирать исходя из положения соседних (для полигона) точек и из соображения гладкости.
Лично для меня еще было совершенно контринтуитивно, как быть с длиной вектора производной. Направление — понятно, а вот длина?
В итоге родился такой алгоритм:
1. На первом этапе происходит некоторая классификация точек. В графе (который задают точки полигонов и их связи) ищутся и запоминаются циклы длиной 4, а кроме того записываются соседи, наиболее подходящие на роль продолжения ребра полигона (заранее определяется, какие ребра соответствуют изменению параметра u, а какие — v). Вот кусок кода, который ищет, сортирует и запоминает соседей для 0-й точки какого-то цикла:
Скрытый текст
""" схематичное расположение точек:
cykle[5] cykle[7]
cykle[4]--cykle[0] --u-- cykle[1]-cykle[6]
|v |v
cykle[10]-cykle[3] --u-- cykle[2]-cykle[8]
cykle[11] cykle[9]
"""
sosed = []
for i in range(0, N):
if self.connects[i][ind] == 1 and i != cykle[0] and i != cykle[1] and i != cykle[3]:
sosed += [i] #в нашем доме поселился замечательный...
if(len(sosed) < 2):
continue #пока такое не обрабатываем
else:
#вычисляем длины векторов между соседями точки cykle[0]
vs0c3 = MinusVecs(self.dots[sosed[0]], self.dots[cykle[3]])
vs1c1 = MinusVecs(self.dots[sosed[1]], self.dots[cykle[1]])
#есть два варианта и один из них длиннее
vs0c1 = MinusVecs(self.dots[sosed[0]], self.dots[cykle[1]])
vs1c3 = MinusVecs(self.dots[sosed[1]], self.dots[cykle[3]])
Rvsc = [ScalMult(vs0c3,vs0c3),ScalMult(vs1c1,vs1c1),ScalMult(vs0c1,vs0c1),ScalMult(vs1c3,vs1c3) ]
n1 = Rvsc.index(max(Rvsc))
if n1 < 2:
cykle += [sosed[1],sosed[0]] #сначала по u потом по v
else:
cykle += [sosed[0],sosed[1]]Дальше, при построении сплайна, производная вдоль ребра (например по параметру u) в точке полигона выбирается исходя из расположения двух точек ребра и одной соседней точки (пусть это будут точки vec1, vec2 и vec3; точка в которой ищется производная — вторая).

Сначала я пытался использовать для этой роли нормированный вектор vec3 — vec1 (типа применил теорему Лагранжа), но проблемы возникли именно с длиной вектора производных — делать его константой было плохой идеей.
Лирическое отступление:
Для небольшой иллюстрации, что такое вектор производной в параметрическом варианте, обратимся к простой двумерной аналогии — вот кусок дуги окружности:

Т.е. модуль производной = R*pi/2 и, вообще говоря, зависит от размера куска дуги, который мы задали через параметр.
Что же с этим теперь делать? Лев Николаевич Толстой завещал нам, что все круглое = хорошее, поэтому, если мы зададим производную в точке так, как если бы хотели построить там дугу, — у нас получится гладкая красивая кривая.
Конец лирического отступления.
Второй этап поиска производной:
2. Через наши три точки vec1, vec2, vec3 строим плоскость, в этой плоскости ищем окружность, которая проходит через все три точки. Искомая производная будет направлена по касательной к окружности в точке vec2, а модуль вектора производной должен равняться произведению радиуса окружности и угла сектора, который образуют две точки грани полигона (аналогично нашей простой плоской аналогии из лирического отступления).
Вроде все просто, вот код функции, например (опять используется NumPy):
не код, а...
def create_dd(vec1, vec2, tuda, vec3):
"""делает вектор производной для отрезка 1-2 во второй точке в направлении точки 3 если туда == 1"""
#0. убедиться что точки не лежат на одной прямой - в этом случае окружность через них не провести :(
vecmult = VecMult(MinusVecs(vec2,vec1),MinusVecs(vec3,vec1)) #векторное произведение vec2-vec1 x vec3 - vec1
if vecmult[0]*vecmult[0] + vecmult[1]*vecmult[1] + vecmult[2]*vecmult[2] < 0.000001: #ну почти 0
if tuda == 1:
return NormVec(MinusVecs(vec3,vec2))
else:
return NormVec(MinusVecs(vec1,vec2))
#1. найти центр окружности, проходящей через эти точки
#сначала два условия про то что расстояния до центра одинаковые порождают 2 линейных уравнения
M = np.zeros((3,3),float)
C = np.zeros((3,1),float)
M[0][0] = 2*vec2[0] - 2*vec1[0]
M[0][1] = 2*vec2[1] - 2*vec1[1]
M[0][2] = 2*vec2[2] - 2*vec1[2]
C[0] = -vec1[0]*vec1[0] - vec1[1]*vec1[1] - vec1[2]*vec1[2] + vec2[0]*vec2[0] + vec2[1]*vec2[1] + vec2[2]*vec2[2]
M[1][0] = 2*vec3[0] - 2*vec2[0]
M[1][1] = 2*vec3[1] - 2*vec2[1]
M[1][2] = 2*vec3[2] - 2*vec2[2]
C[1] = -vec2[0]*vec2[0] - vec2[1]*vec2[1] - vec2[2]*vec2[2] + vec3[0]*vec3[0] + vec3[1]*vec3[1] + vec3[2]*vec3[2]
#еще одно уравнение указывает, что все 4 вектора в одной плоскости
M[2][0] = vecmult[0]
M[2][1] = vecmult[1]
M[2][2] = vecmult[2]
C[2] = vecmult[0]*vec1[0] + vecmult[1]*vec1[1] + vecmult[2]*vec1[2]
# M * вектор центра окружности = C
Mobr = np.linalg.inv(M)
Rvec = np.dot(Mobr,C)
res = NormVec(VecMult(MinusVecs(Rvec,vec2), vecmult)) #направление с точностью до знаka
#R = math.sqrt((Rvec[0]-vec1[0])**2 + (Rvec[1]-vec1[1])**2 + (Rvec[2]-vec1[2])**2)
#длина вектора производной = 3.14*2*asin(l/(2*R))/180 * R, но можно попытаться заменить на l с коэффициентом, взятым с потолка
l = 1.2*math.sqrt((vec1[0]-vec2[0])**2 + (vec1[1]-vec2[1])**2 + (vec1[2]-vec2[2])**2)
if ScalMult(res, MinusVecs(vec2, vec1)) > 0: #вектор смотрит в ту сторону
return MultVxC(res, tuda*l)
else:
return MultVxC(res, -tuda*l)
Ну и в общем, это все как-то работает. Для демонстрации я взял куб 5х5х5 и менял положение точек рандомайзером:
гифка, 8Мб






