Есть простая последовательность чисел
В принципе, ничего особенного, и программируется очень легко. Вот первые несколько элементов этой последовательности
Последовательность (не строго) монотонно стремится к нулю. Нетрудно оценить примерное поведение при больших n:
С этой константой C связана захватывающая история. Я отправил вопрос на mathstackexchange.com. Через некоторое время пользователь Тиан Влашич указал что "база знаний" Wolfram Alpha определила возможное значение по десятичным знакам как
Там предлагалось несколько вариантов, и Тиян выбрал правильный. Но как это доказать? Я некоторое время работал над генерирующей функцией для последовательности a_n, и наконец нашёл для неё как мне показалось красивое интегральное уравнение. Тут же я отправил другой вопрос, уже на mathoverflow.net. Через пару дней известный математик Федя Назаров доказал, что эта функция в нуле равна 1-ln(2), что и требовалось для моей константы. Его метод был довольно зрелищным, при этом он вернулся к дифференциальному уравнению, предложенному другим участником обсуждения, и выделил дискретную подпоследовательность, которая вела себя как ln(2). Вдохновившись тем, что задача может быть решена, на следующий день я нашёл своё доказательство, без дифференциальных уравнений, с помощью рекурсивного интегрирования по частям интегрального уравнения. Но вернёмся к последовательности. Мы нашли только первое приближение на бесконечности, а как быть со следующими слагаемыми асимптотики? Раз последовательность стремится к нулю, и, забегая вперёд, самое интересное происходит, в пятом слагаемом асимптотики, давайте её отнормируем, сразу на n^2, а точнее определим
На самом деле последовательность фи была изначально, это потом я превратил её в a_n, которая выглядит совсем просто. Ладно, давайте подробнее. Последовательность фи связана с редкими событиями в ветвящемся процессе в случайном окружении. Это одна из простейших задач, но, как оказалось, уже она довольно трудная. Есть одна частица, за один шаг она делится с вероятностью p на две частицы, или с вероятностью 1-p остаётся одной. То же самое происходит с порождёнными частицами. При этом p на каждом шаге выбирается случайно из интервала (0,1).Если X_t количество частиц на t-ом шаге, то
То есть последовательность фи показывает насколько быстро растёт количество частиц по сравнению со случаем, когда деления частиц не было ни на одном из шагов. Это изначальная задача, но не суть. Так или иначе, посчитав a_n, а затем и фи по формулам выше, строим график
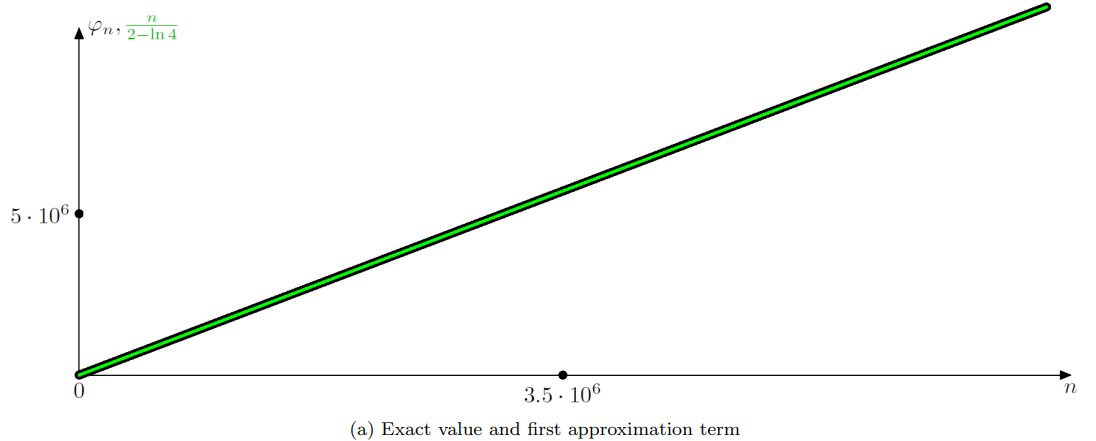
Замечательно, линейный рост со странным множителем. Немного повозившись с производящей функцией я выделил второе слагаемое асимптотики и построил его

На самом деле это последовательность с периодом 2. Ничего удивительного, учитывая форму последовательности a_n, где соседние элементы повторяются. Два значения во втором слагаемом асимптотики можно сосчитать явно, они выражаются через константу C - самое сложное было найти её точное значение. Пойдём далее и построим третье слагаемое асимптотики

Здесь уже стандартной двойной точности не хватает. Я программирую на Delphi, и потому использовал быструю библиотеку NesLib, удвоив стандартную точность. Вот исправленная картинка - четвёртое слагаемое асимптотики оказалось делённой на n последовательностью периода 4, которую тоже можно вычислить явно

Раз уж обзавелись хорошей точностью, к тому же очень быстро работающей, пойдём ещё дальше

Здесь уже последовательность периода 8, делённая на n^2. Мы видим только 6 слагаемых, потому что два совпадают с остальными. Вот явные значения этой последовательности

Конечно же, где-то дальше в асимптотике будет последовательность периода 16 делённая на n^3, и так далее. Но в пятом слагаемом асимптотики произошло что-то странное

Оно есть вовсе не то что мы ожидали. Его порядок не 1/n^3 и период не постоянный дискретный, а логарифмический и непрерывный. Отметим что аналитическое выражение асимптотических параметров через логарифм в предыдущих слагаемых весьма важно, потому что остатки малы, и любая неточность в константах сильно затруднит вычисление следующих слагаемых - мы бы никогда не добрались до этой осцилляции. Так что это за числа такие 2.54536... и 10.75397...? На самом деле

это один из комплексных корней уравнения
Все корни этого уравнения, с прибавленными к ним натуральными числами будут вносить вклад в асимптотику. Особенность комплексных корней, а таких корней бесконечно много - это их осциллирующий вклад. Поскольку мнимая часть комплексных корней может быть сколь угодно большой, осцилляции тоже будут со сколь угодно большой частотой. Правда степенной множитель таких осцилляций будет мал. Ещё скажу, что я не знаю как выразить амплитуду осцилляций через известные константы. Через логарифм двух я могу выразить только неосциллирующие элементы асимптотики. А для осциллирующих это пока открытая проблема. Да, частота и степенной множитель - это корни уравнения, указанного выше, но что есть сами амплитудные константы? Настолько глубока кроличья нора даже для таких несложных числовых последовательностей.