Теория игр как механизм для анализа крупномасштабных данных

Современные системы искусственного интеллекта подходят к решению таких задач, как распознавание объектов на изображениях и прогнозирование трёхмерной структуры белков, как прилежный студент готовится к экзамену. Тренируясь на многих примерах решения аналогичных задач, они со временем сводят к минимуму собственные ошибки и в конце концов добиваются успеха. Но приведённый пример — лишь частный случай и лишь одна из известных форм обучения. К старту курса "Machine Learning и Deep Learning" делимся переводом статьи о том, как в DeepMind создали многоагентную систему при помощи нового подхода EigenGame, то есть компромисса между чистой оптимизацией и динамической системой.

Обучение также происходит при взаимодействии и играх с другими людьми. Перед человеком могут вставать чрезвычайно сложные проблемы, и решить их в одиночку ему вряд ли удастся. DeepMind попыталась решать проблемы с использованием определённых игровых приёмов, и у неё это прекрасно получилось — она обучила агентов ИИ играть в Capture the Flag, а один из её агентов даже набрал гроссмейстерскую норму в Starcraft [мы писали об этом вчера, в статье о том, как StarCraft II может помочь экологам]. Это заставило нас задуматься, сможет ли теория игр помочь в решении других фундаментальных проблем машинного обучения.

Сегодня на ICLR — 2021 (Международной конференции по обучающим представительствам) мы представили исследование "EigenGame: метод PCA как равновесие по Нэшу", получившее награду за лучшую публикацию (Outstanding Paper Award). В нём мы описали новый подход к решению старой проблемы: представили метод главных компонент (PCA), тип задачи о собственных значениях как конкурентную многоагентную игру. Такую игру мы назвали EigenGame. Метод PCA обычно трактуется как задача оптимизации (или проблема одного агента); однако мы выяснили, что, если применить многоагентный подход, можно разрабатывать новые идеи и алгоритмы, использующие современные вычислительные ресурсы. Применяя многоагентный подход, мы научились масштабировать огромные наборы данных, обработка которых ранее занимала бы слишком много времени и ресурсов, и теперь предлагаем альтернативный подход к проведению будущих исследований.

Метод PCA как равновесие Нэша

Впервые описанный в начале 1900-х годов метод PCA представляет собой давнюю технику, позволяющую осмыслить структуру крупномасштабных данных. В настоящее время данный подход повсеместно используется в качестве средства, обеспечивающего первый этап работы конвейера обработки данных и позволяющего с лёгкостью кластеризовать и визуализировать данные. Данный метод также может оказаться полезным инструментом для обучения низкоразмерных представлений функциям регрессии и классификации. Со времени изобретения метода PCA прошло уже более века, но до сей поры он не утратил своей актуальности.

Во-первых, раньше данные заносились вручную в бумажные блокноты, их было не так много, и их обработка не представляла сложности, а сейчас они хранятся в центрах обработки данных огромных размеров, и применение метода требует колоссальных вычислительных ресурсов. Исследователи пытались применять рандомизированные алгоритмы и другие методы, повышающие качество масштабирования метода PCA, однако, как удалось выяснить, такие подходы практически неприменимы к массивным наборам данных, так как неспособны в полной мере использовать последние достижения вычислительной науки, ориентированные на глубокое обучение, а именно доступ ко многим параллельным GPU или TPU.

Во-вторых, метод PCA имеет много общего с множеством важных инженерных методов и алгоритмов машинного обучения, в частности с методом разложения по сингулярным значениям (SVD). Благодаря правильно выбранному подходу к применению метода PCA наши идеи и алгоритмы стали широко применяться во всех областях машинного обучения.

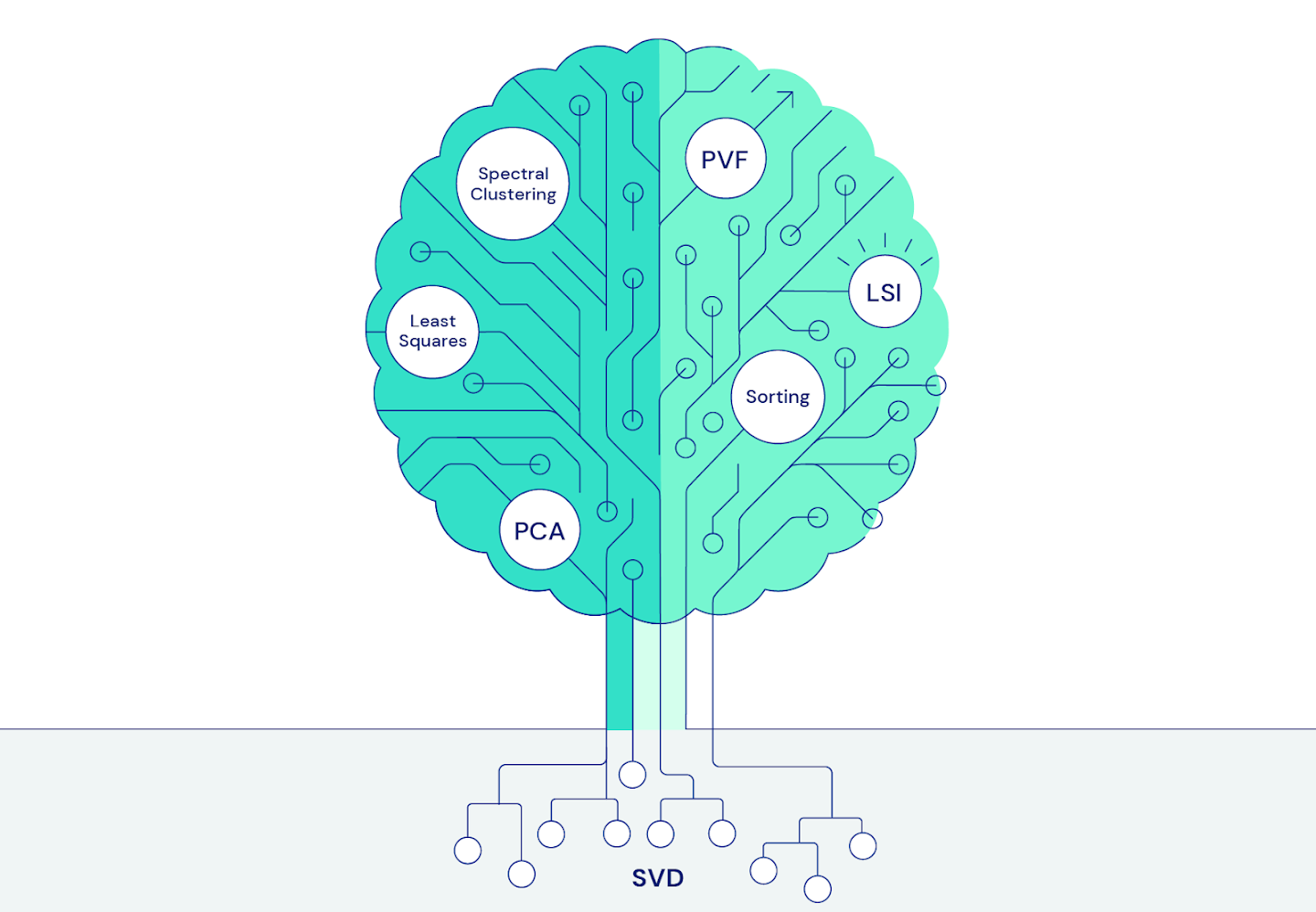
Как и в любой настольной игре, для того чтобы представить метод PCA в качестве игры, необходим набор правил и целей, которым должны следовать игроки. Существует множество возможных способов разработки такой игры; вероятно, лучшим из них является концепция самого метода PCA: оптимальное решение состоит из собственных векторов, отражающих важную дисперсию данных и ортогональных друг другу.

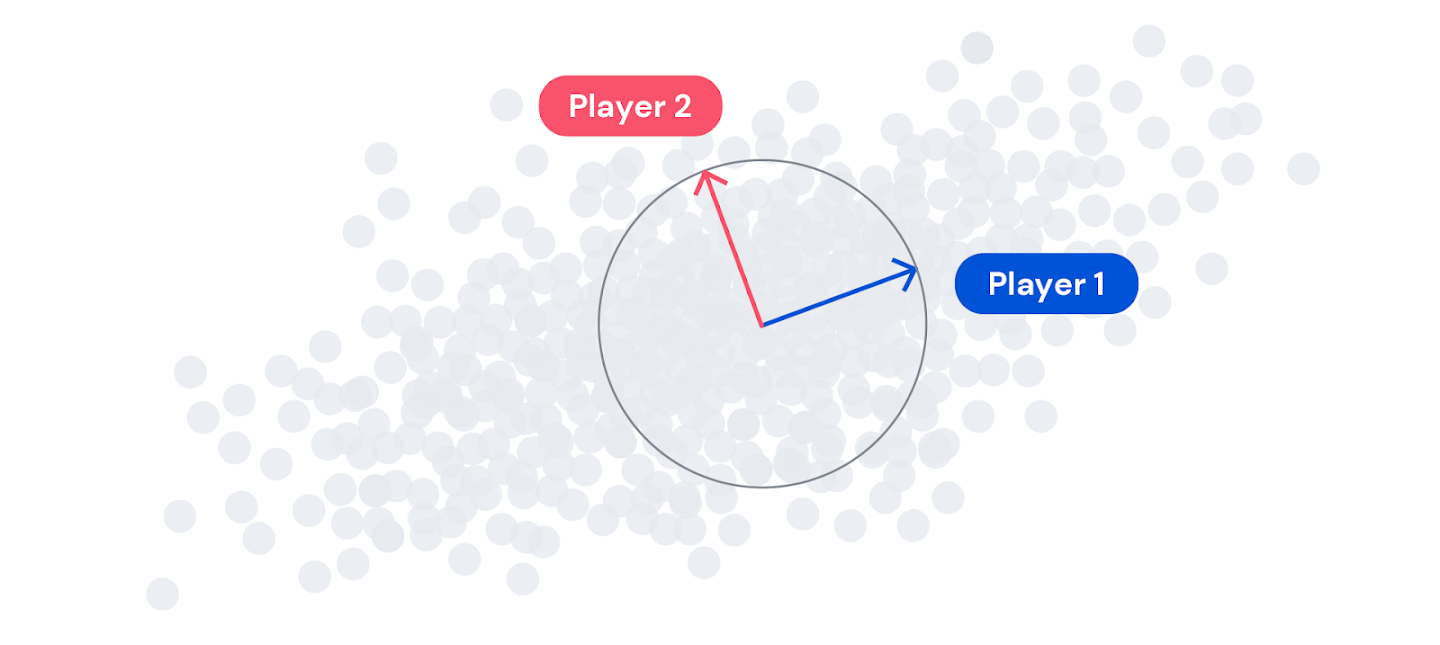
В игре EigenGame каждый игрок управляет собственным вектором. Игроки увеличивают свой счёт, объясняя дисперсию в данных, но получают штраф, если слишком близко "подходят" к другим игрокам. Мы также устанавливаем иерархию: игрока 1 волнует только максимизация дисперсии, в то время как другие игроки также должны беспокоиться о том, чтобы не "подходить" близко к игрокам, стоящим выше их в иерархии. Такое сочетание поощрений и наказаний определяет полезность каждого игрока.

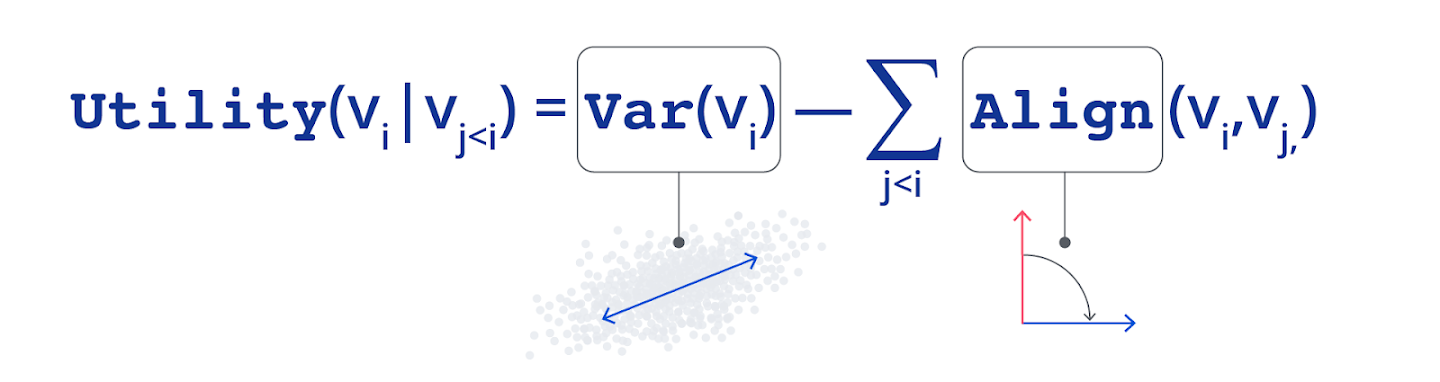
С помощью надлежащим образом определённых Var и Align можно показать, что:

• Если все игроки играют оптимально, вместе они достигают равновесия по Нэшу, что и является решением PCA.

• Такого результата можно достичь, если каждый игрок независимо и одновременно максимизирует собственную полезность, используя градиентное восхождение.

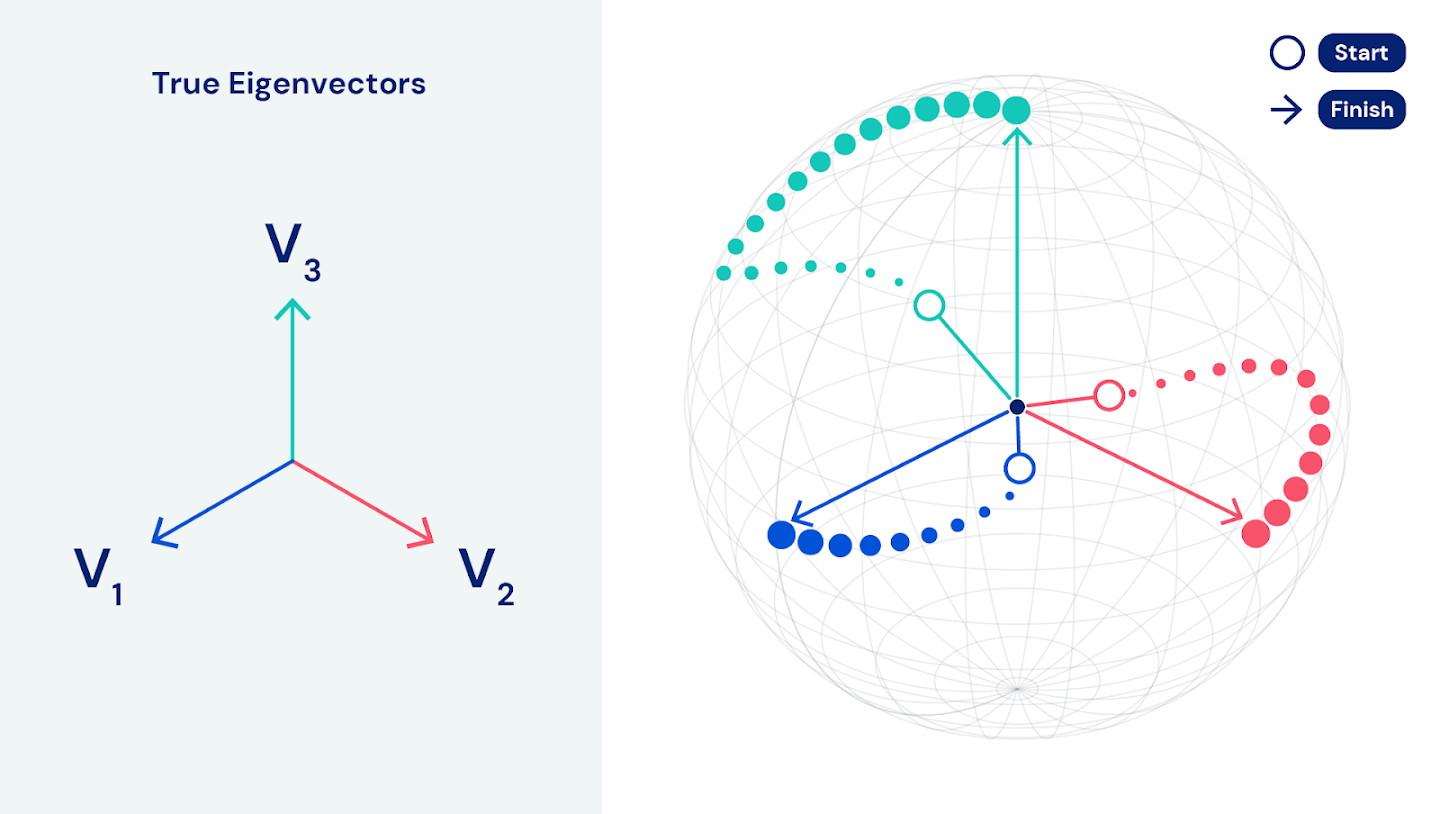
Данное свойство независимости одновременного восхождения имеет особенную важность, так как позволяет распределить вычисления по десяткам TPU в Google Cloud, обеспечивая параллелизм данных и моделей. Соответственно, наш алгоритм может адаптироваться к данным действительно крупного масштаба. Для наборов данных из сотен терабайт, содержащих миллионы признаков или миллиарды строк, EigenGame находит главные компоненты за несколько часов.

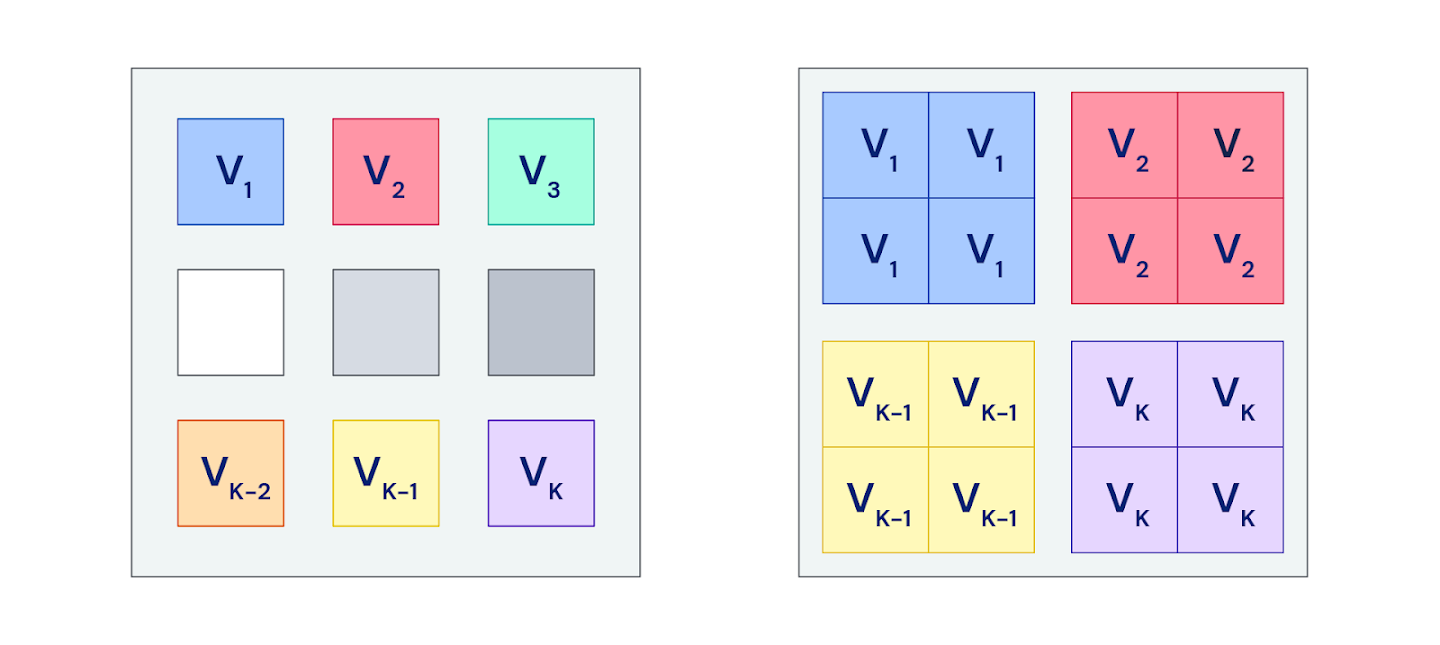
Полезность, обновления и всё, что с ними связано

Применяя метод PCA как многоагентную функцию, мы смогли разработать масштабируемые алгоритмы и предложить новые метода анализа. Мы также обнаружили удивительную связь метода с обучением по Хеббу, то есть тем, как происходит адаптация нейронов в процессе обучения. В EigenGame каждый игрок, максимизирующий собственную полезность, запускает уравнения обновления, аналогичные правилам обновления, полученным на основе Хеббовских моделей мозговой синаптической пластичности. Известно, что обновления по Хеббу сводятся к решению проблемы PCA, однако они не выводятся как градиент какой-либо функции полезности. Теория игр предоставляет возможность по-новому взглянуть на обучение по Хеббу, а также предлагает большое разнообразие подходов к решению проблем машинного обучения.

На одном конце разнообразных методов машинного обучения находится хорошо отработанный путь предложения целевой функции, которую можно оптимизировать: используя теорию выпуклого и невыпуклого программирования, исследователи могут рассуждать о глобальных свойствах решения. С другой стороны, чистые нейросетевые методы и правила обновления, созданные на основе нейробиологических концепций, задаются напрямую, однако задача анализа всей системы может оказаться более сложной, часто требующей анализа сложных динамических систем.

Теоретико-игровые подходы, такие как EigenGame, находятся где-то посередине. Обновления игрока не ограничиваются градиентом функции, а только наилучшим ответом на текущие стратегии других игроков. Мы можем свободно проектировать функции полезности и обновления с желаемыми свойствами, например, определять нейтральные или ускоренные обновления, гарантируя при этом, что для анализа системы в целом по-прежнему будет использоваться правило Нэша.

EigenGame реализует конкретный пример разработки решения задачи машинного обучения в качестве выхода большой многоагентной системы. В целом разработка задач машинного обучения как многоагентных игр представляет собой сложную проблему разработки механизмов; однако для решения задач машинного обучения исследователи уже используют класс игр с нулевой суммой для двух игроков. В частности, успех генеративных состязательных сетей (GANs) как подхода к генеративному моделированию вызвал интерес к взаимосвязи между теорией игр и машинным обучением.

EigenGame идёт ещё дальше, создавая более сложную игру для многих игроков с накопленной суммой, обеспечивающую более очевидный параллелизм и, соответственно, больший масштаб и скорость. Данная игра также представляет собой количественный эталон для игрового сообщества, позволяющий тестировать новые многоагентные алгоритмы в более перспективных областях, таких как дипломатия и футбол.

Надеемся, что наш план разработки функций полезности и обновлений побудит других энтузиастов исследовать данное направление и начать разрабатывать собственные алгоритмы, агентов и системы. В перспективе хотелось бы выяснить, какие ещё проблемы могут быть сформулированы как игры и смогут ли полученные нами знания улучшить понимание многоагентной природы интеллекта.

Более подробная информация приведена в нашей работе EigenGame: метод PCA как равновесие по Нэшу и последующей работе EigenGame Unloaded: когда играть лучше, чем оптимизировать. Данная запись в блоге основана на совместной работе с Туром Грейпелом, руководителем исследовательской группы в DeepMind и заведующим кафедрой машинного обучения в Университетском колледже Лондона.

Машинное обучение продолжает развиваться, приобретая гибкость, необходимую для решения проблем всё более широкого спектра, а значит её проблемы и решения будут актуальны ещё долгое время по меркам не только быстро изменяющихся информационных технологий, но и других областей знаний, где новые методы будут применяться. Если вам интересна сфера глубокого и машинного обучения, вы можете обратить внимание на курс "Machine Learning и Deep Learning" — широкое и глубокое введение в область искусственного интеллекта.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

• Профессия Data Scientist

• Профессия Data Analyst

• Курс по Data Engineering