В данной статье приведены описание и алгоритм решения задачи построения рисунка внутренностей месторождения, являющегося результатом пересечения расчётной сетки с плоскостью. А также приведены тайминги построения решения, которые получаются на типичном компьютере геолога-модельера или гидродинамика.
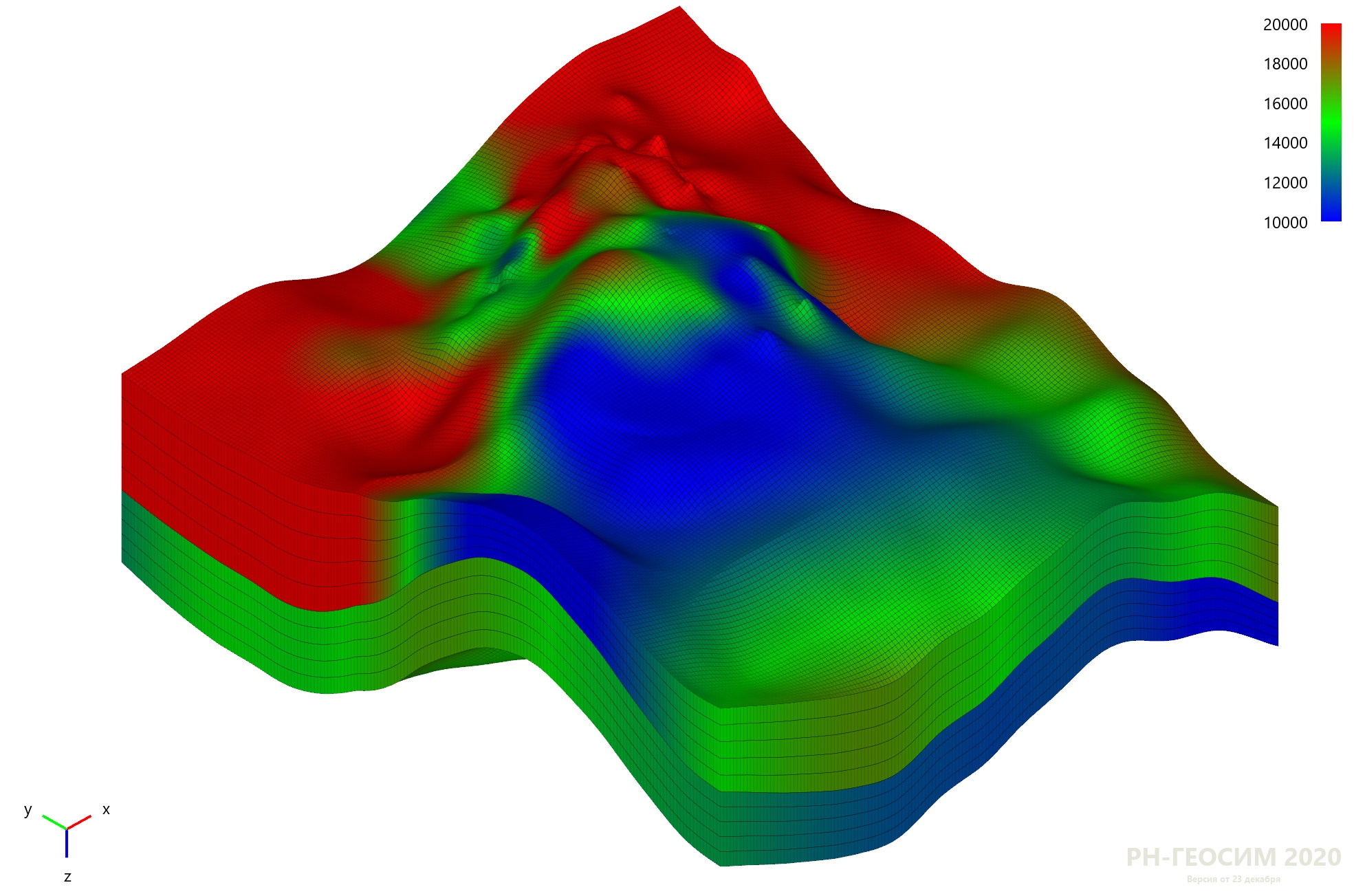
Визуализация расчётной сетки и куба
Моделирование месторождений уже упоминалось ранее в предыдущих наших обзорах (https://habr.com/ru/company/bashnipineft/blog/512052/). При построении 3D-моделей нефтегазовых месторождений в различных областях – в гидродинамике, в геологии, в механике – часто используются объёмные расчётные сетки. Также сетки нужны, например, при использовании метода конечных объёмов.
Одним из типовых видов расчётных сеток при моделировании коллектора (т. е. среды, где находится нефть) являются сетки, в которых каждая ячейка представлена шестигранником с четырехугольными гранями (ячейка похожа на помятый кубик). Непосредственно расчётная сетка описывает геометрию моделируемого месторождения, количество ячеек сетки обычно от нескольких миллионов до порядка миллиарда. Для моделирования физических свойств месторождения (например, пористости или проницаемости) расчётные сетки заполняются многочисленными массивами данных, называемыми кубами. Кубы описывают характеристики пород или фильтрационно-емкостные свойства месторождения.
Часто пользователю, который работает с моделью, нужно визуально оценить распределение физических свойств внутри модели месторождения. Это можно делать разными способами, например, созданием сечений или наложением масок-фильтров на ячейки сетки.
Реализовать в программе визуализацию слоев (i, j, k) сетки довольно просто и быстро.

Визуализация слоев сетки i, j (“слайсов”)
Однако хотелось бы получать рисунок вдоль произвольной плоскости, при этом иметь возможность двигать и крутить эту плоскость в произвольном направлении с хорошим FPS. Таким образом, модельеру нужен этакий быстрый «томограф» модели месторождения.
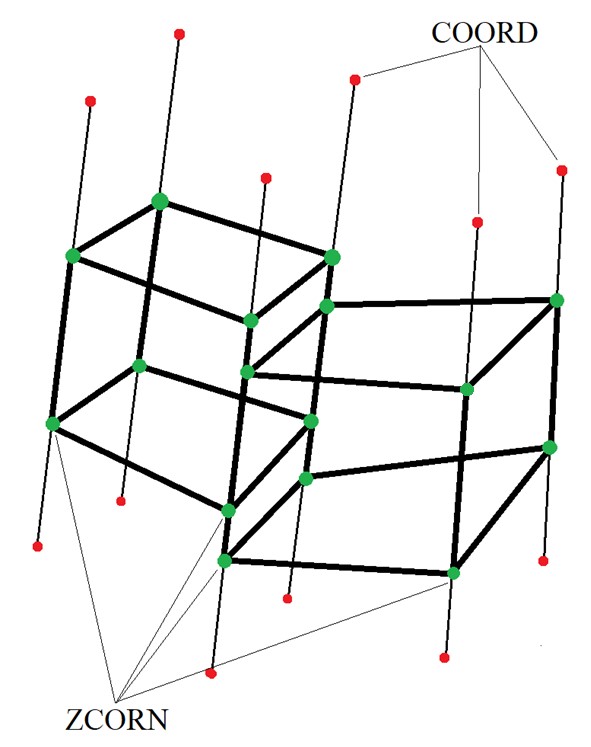
Геометрия угловой точки (corner-point grid) – способ задания геометрии расчётных сеток из шестигранников, наиболее часто использующийся в гидродинамическом и геологическом моделировании. Такой формат подразумевает:
• Наличие пилларов – отрезков, каждый из которых задан двумя точками, а каждая точка – тремя координатами (x, y, z). Пиллары могут быть вертикальными, наклонными, но никак не горизонтальными. Пиллары образуют множество размером M x N, но не обязательно с постоянным шагом. Множество пилларов задаётся массивом COORD.
• На пиллары накидываются отметки вершин, у которых известна лишь координата z (глубина). Для каждой ячейки нужно по восемь отметок – по две на четыре соседних пиллара. Эти отметки точек по сути своей являются углами ячеек, поэтому формат и называется «геометрия угловой точки». Множество отметок задается массивом ZCORN. Ячейки не могут пересекаться друг с другом. Соседние ячейки не обязательно стыкуются друг с другом, поэтому даже при полном совпадении вершин граней соседних ячеек эти вершины дублируются.
• Кроме этого, задаётся массив нулей и единиц ACTNUM. Нулевое значение в ячейке указывает на то, что она неактивна и её не стоит учитывать в расчётах.
Геометрия угловой точки
Входными данными для задачи построения сечения являются:
Решение не обязательно должно быть точным, ведь решение будет оцениваться пользователем только визуально. На выходе должны получиться массивы:
Такой формат выбран потому, что он удобен и для визуализации через векторные графические движки, и для визуализации через триангуляционные движки.
Хорошо бы, чтобы алгоритм построения пересечения был нетребователен к памяти, так как сами сетки довольно объёмны. Например, большая сетка на 1000х1000х1000 ячеек, построенная на типе данных одинарной точности (float) занимает примерно 30 гигабайт памяти.
Нами был разработан довольно экономный к памяти алгоритм построения пересечения геометрии угловой точки и плоскости:
1. Проход по всем ячейкам и определение факта пересечение плоскости с ячейкой:
a. Подстановка каждой вершины в левую часть уравнения плоскости.
b. Если среди полученных чисел есть хотя бы два с противоположными знаками, то пересечение есть.
c. Если среди полученных чисел есть хотя бы три нуля, то пересечение есть.
d. Запись в массив флагов факта пересечения.
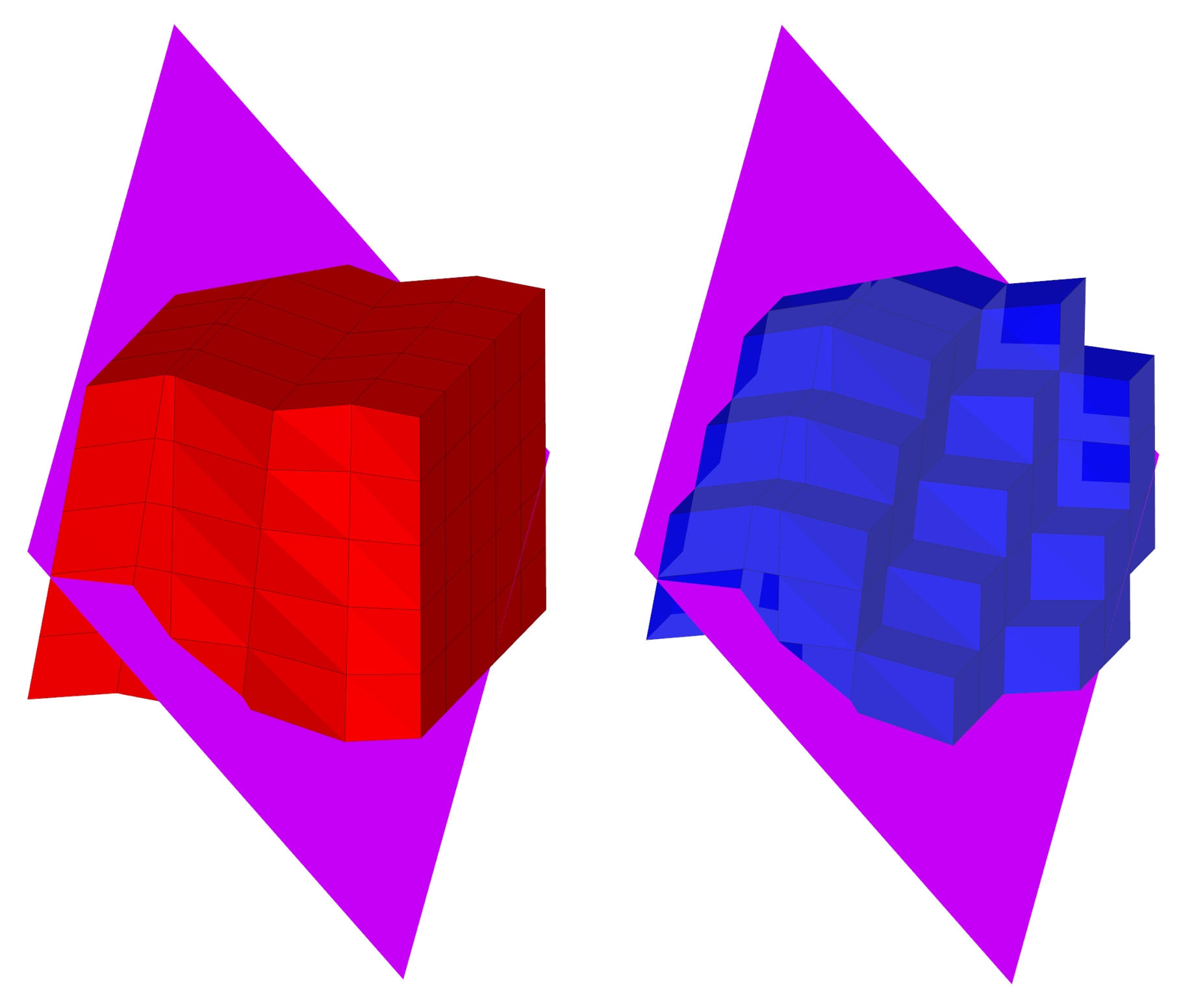
Геометрия угловой точки, секущая плоскость, пересечённые ячейки
2. Stream Compaction: из массива флагов собираем индексы ячеек, которые пересекаются с плоскостью. Располагаем их в новом массиве компактно.
3. Для каждой пересекаемой ячейки определяем количество точек пересечения – проход по всем вершинам и всем рёбрам ячейки. Складываем значения количества точек пересечения соответственно индексам ячеек в общий массив количества точек пересечения.
4. Prefix sum: префиксная сумма по массиву количества точек пересечения в ячейках. Это позволит определить смещение от начала массива координат точек для каждой ячейки.
5. Поиск и запись точек пересечения в массив координат точек пересечения.
6. Для каждой пересечённой ячейки находим барицентр точек пересечения. Составляем вектора по каждой точке пересечения и барицентру. Сортируем точки пересечения по углу относительно первого вектора, тем самым упорядочиваем точки в полигон.
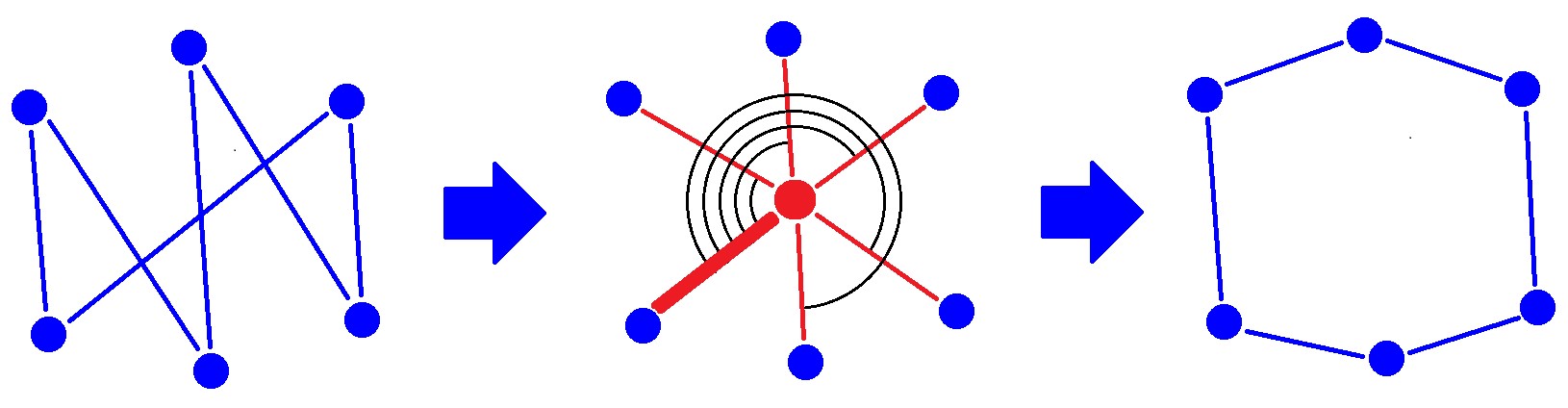
Упорядочивание точек пересечения для одной ячейки в полигон
Таким образом получаем результирующие массивы координат полигонов и индексов начальных точек полигонов.

Результат пересечения геометрии угловой точки и плоскости
Видно, что каждый шаг алгоритма можно распараллелить.
Была создана реализация алгоритма, распараллеленная на потоки с помощью OpenMP. В такой реализации примерно 87% времени выполнения занимает первый пункт алгоритма – проход по всем ячейкам и определение факта пересечения. Время выполнения реализации на OpenMP оказалось слишком большим для комфортной работы с пересечениями в окнах визуализации.
Чтобы ускорить построение пересечения, алгоритм был реализован на CUDA. Сетка должна быть постоянно в видеопамяти, т. к. пересылка её с оперативной памяти занимает слишком много времени, даже если использовать CUDA Streams. В такой реализации примерно 43% времени выполнения занимает первый пункт алгоритма, 20% времени – пересылка результатов с видеопамяти в оперативную память. Kernel-функция, используемая в реализации для определения факта пересечения, довольно проста:
Для тестирования был взят случай, который даёт большое количество полигонов пересечения. Сетка в тестах состояла из прямоугольных параллелепипедов, по каждому направлению (x, y и z) сетка располагалась от 0 м до 100 м. Плоскость проходила через «центр» сетки и имела нормаль (1, 1, 1).
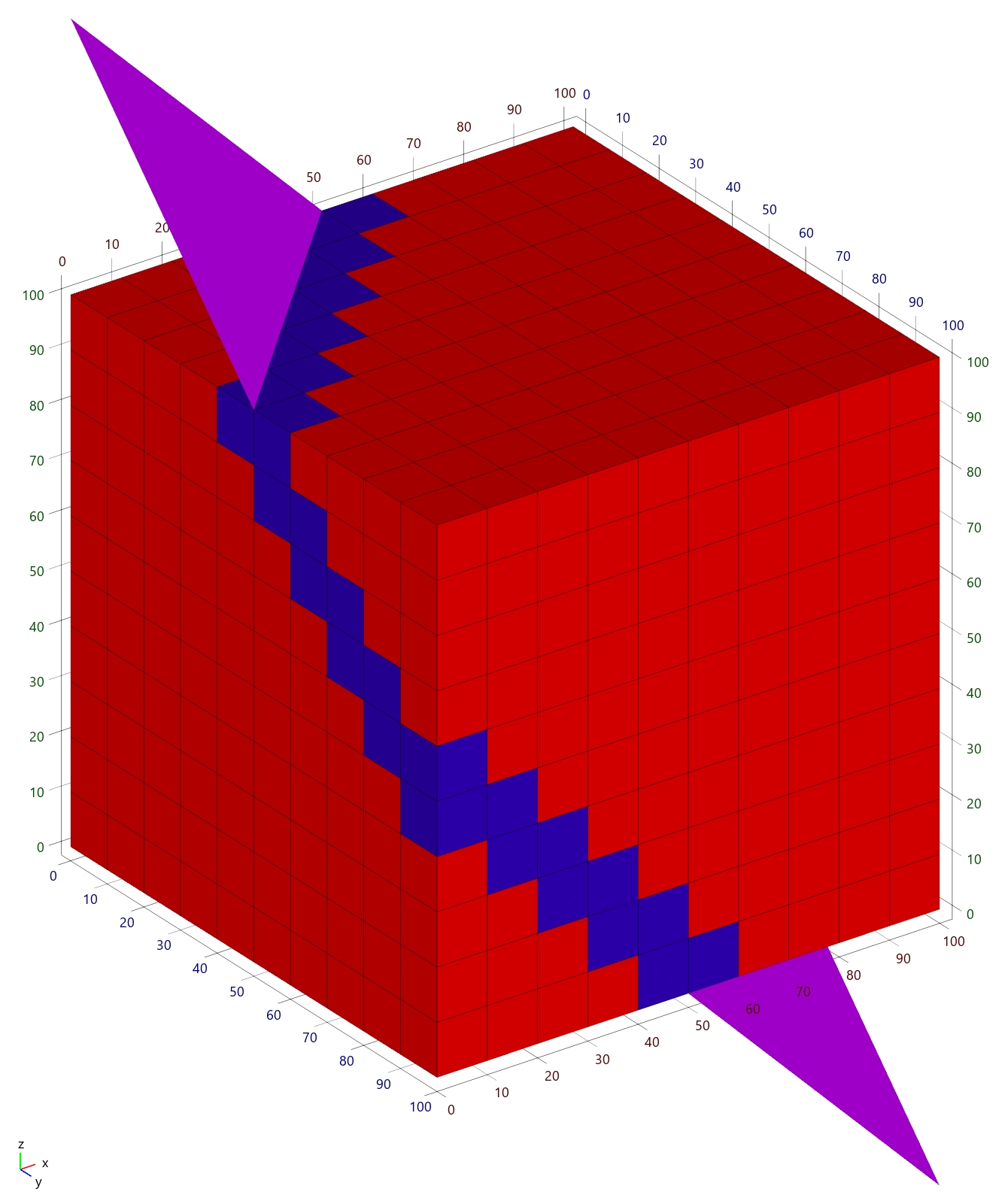
Геометрия угловой точки и секущая плоскость для тестирования
Результаты тестирования и замеры времени выполнения представлены ниже. Тестирование проводилось на одном и том же компьютере.
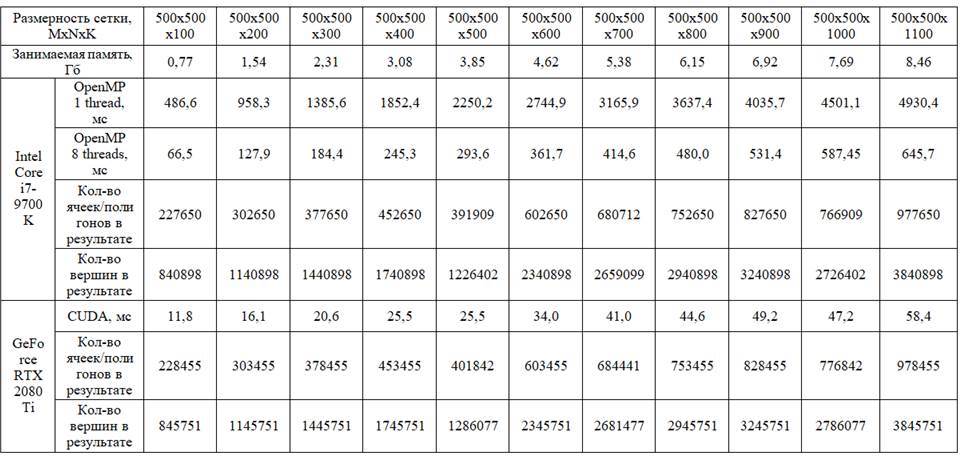
Таблица с результатами тестирования и замерами времени выполнения
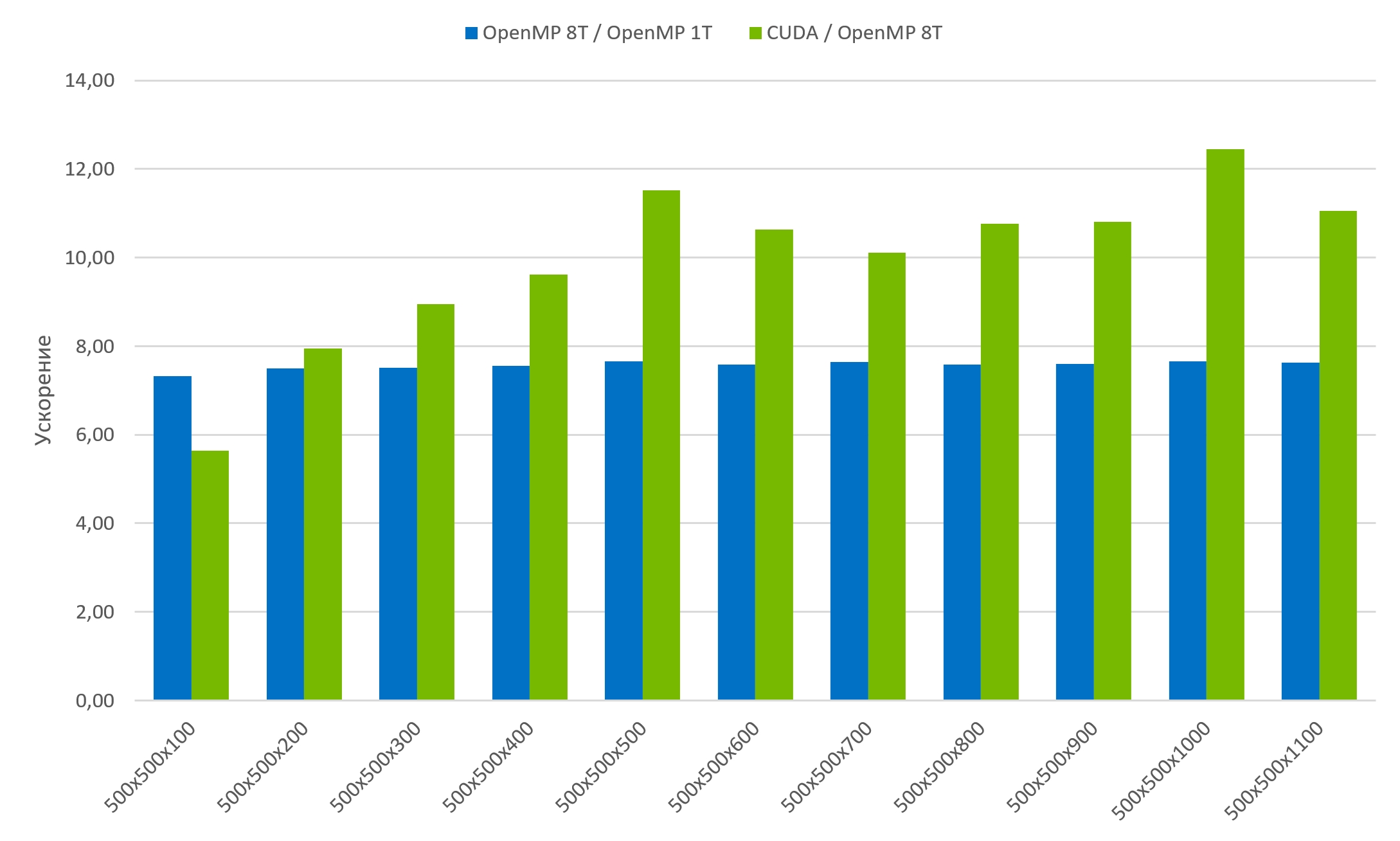
Синяя диаграмма показывает ускорение построения пересечения на OpenMP на 8 потоках относительно OpenMP на 1 потоке. Зелёная диаграмма показывает ускорение построения пересечения на CUDA относительно OpenMP на 8 потоках
Из результатов замеров времени выполнения видно, что, используя реализацию на CUDA, можно добиться практически незамедлительного построения пересечения больших сеток. А учитывая то, что CUDA и OpenGL функционально совместимы, то результат построения можно не пересылать с видеопамяти в оперативную память, что ускорит время решения задачи примерно на 20%.
Также видно, что количество вершин в результате пересечения незначительно отличается. Это происходит в случае, когда плоскость касается угла ячейки. Из-за точности расчётов в результате может засчитаться в пересечение очень маленький треугольник, а может и быть пропущен. Результат различается не только между построением на CPU и GPU, но также и между построением на различных CPU и на различных GPU.
Пересечение геометрии угловой точки и плоскости обычно просматривают в 3D окне.
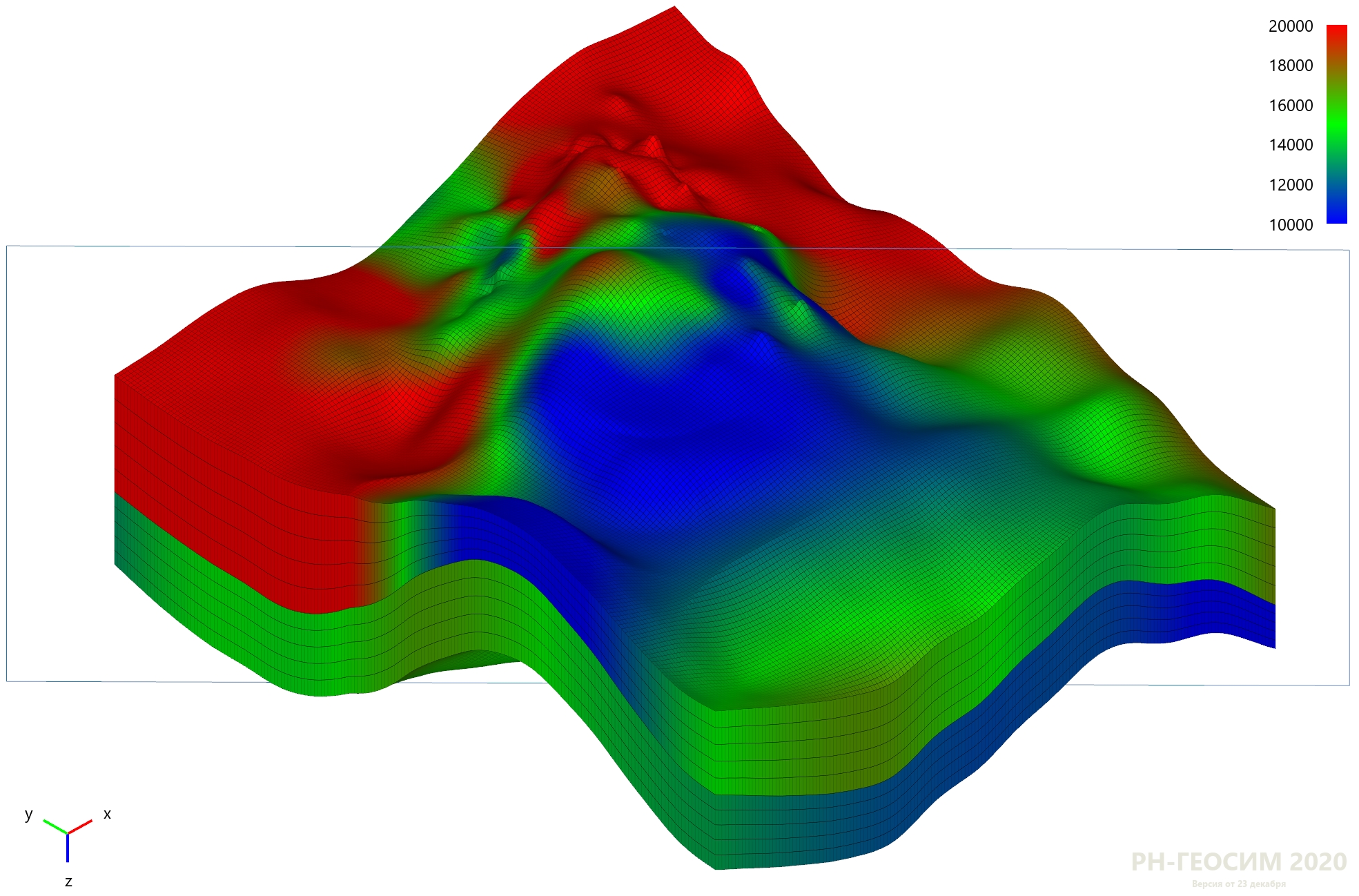
Модель месторождения и секущая плоскость
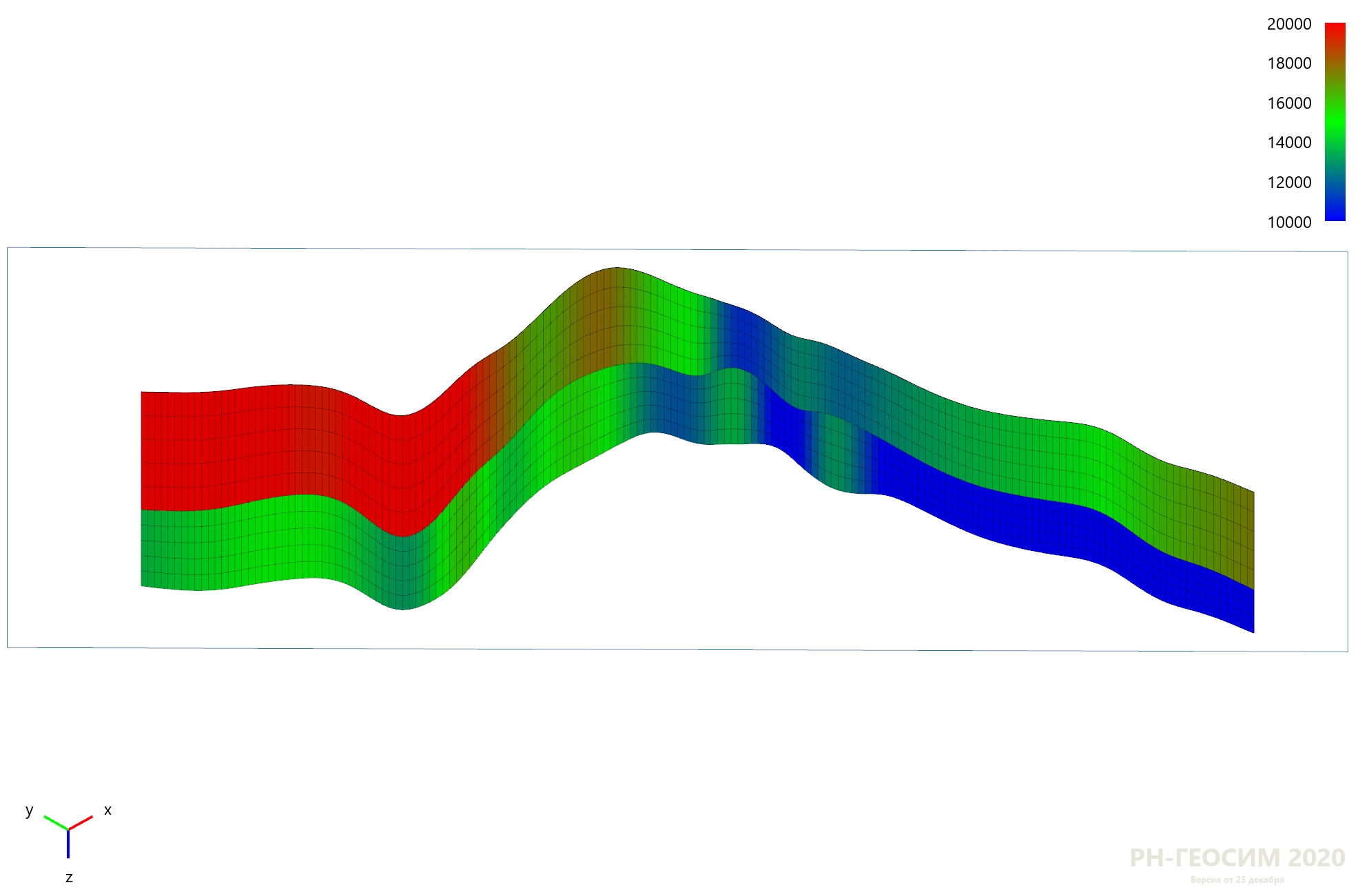
Результат пересечения модели месторождения и плоскости
Заключение: в статье показан пример решения одной из многих задач, возникающих при создании программного обеспечения для процессов моделирования месторождений нефти и газа. Несмотря на огромный парк open-source кодов, решение подобных задач требует мультидисциплинарной подготовки разработчиков, и поэтому представляется интересными развивающими вызовами в области computer science, в которых доля рутинного программирования минимальна, а мозги надо включать «на полную». Этим и интересны задачи нашей предметной области, к которым хотелось бы привлечь внимание аудитории и потенциально заинтересованных энтузиастов и разработчиков. В частности, создание построителя пересечения геометрии угловой точки и плоскости являлось задачей на одном из хакатонов, проведённых в 2019 году «РН-БашНИПИнефть» при участии Уфимского Государственного Авиационного Технического Университета (УГАТУ).
Стоит отметить, что результатом 12-часовой работы команд оказались не полностью доработанные и не до конца оптимизированные решения: основной трудностью стало упорядочивание точек пересечения ячейки в полигон, также команды добавляли каждый новый полигон в конец контейнера координат точек, что не поддавалось распараллеливанию.
P. S. Возможно, поиск пересекаемых ячеек был бы быстрее, если бы применялось K-d дерево. Но реализовать такое решение гораздо сложнее, учитывая, что нужно придумать, как удачно построить само дерево поиска и равномерно распараллелить поиск на потоки. К тому же, если даже теоретически поиск ускорить так, чтобы он вообще не занимал времени (сейчас занимает 87% времени), то производительность на OpenMP реализации вырастет в 7.7 раз, что всё равно медленнее, чем реализация на CUDA.

Визуализация расчётной сетки и куба
Моделирование месторождений уже упоминалось ранее в предыдущих наших обзорах (https://habr.com/ru/company/bashnipineft/blog/512052/). При построении 3D-моделей нефтегазовых месторождений в различных областях – в гидродинамике, в геологии, в механике – часто используются объёмные расчётные сетки. Также сетки нужны, например, при использовании метода конечных объёмов.
Одним из типовых видов расчётных сеток при моделировании коллектора (т. е. среды, где находится нефть) являются сетки, в которых каждая ячейка представлена шестигранником с четырехугольными гранями (ячейка похожа на помятый кубик). Непосредственно расчётная сетка описывает геометрию моделируемого месторождения, количество ячеек сетки обычно от нескольких миллионов до порядка миллиарда. Для моделирования физических свойств месторождения (например, пористости или проницаемости) расчётные сетки заполняются многочисленными массивами данных, называемыми кубами. Кубы описывают характеристики пород или фильтрационно-емкостные свойства месторождения.
Часто пользователю, который работает с моделью, нужно визуально оценить распределение физических свойств внутри модели месторождения. Это можно делать разными способами, например, созданием сечений или наложением масок-фильтров на ячейки сетки.
Реализовать в программе визуализацию слоев (i, j, k) сетки довольно просто и быстро.

Визуализация слоев сетки i, j (“слайсов”)
Однако хотелось бы получать рисунок вдоль произвольной плоскости, при этом иметь возможность двигать и крутить эту плоскость в произвольном направлении с хорошим FPS. Таким образом, модельеру нужен этакий быстрый «томограф» модели месторождения.
Геометрия угловой точки (corner-point grid) – способ задания геометрии расчётных сеток из шестигранников, наиболее часто использующийся в гидродинамическом и геологическом моделировании. Такой формат подразумевает:
• Наличие пилларов – отрезков, каждый из которых задан двумя точками, а каждая точка – тремя координатами (x, y, z). Пиллары могут быть вертикальными, наклонными, но никак не горизонтальными. Пиллары образуют множество размером M x N, но не обязательно с постоянным шагом. Множество пилларов задаётся массивом COORD.
• На пиллары накидываются отметки вершин, у которых известна лишь координата z (глубина). Для каждой ячейки нужно по восемь отметок – по две на четыре соседних пиллара. Эти отметки точек по сути своей являются углами ячеек, поэтому формат и называется «геометрия угловой точки». Множество отметок задается массивом ZCORN. Ячейки не могут пересекаться друг с другом. Соседние ячейки не обязательно стыкуются друг с другом, поэтому даже при полном совпадении вершин граней соседних ячеек эти вершины дублируются.
• Кроме этого, задаётся массив нулей и единиц ACTNUM. Нулевое значение в ячейке указывает на то, что она неактивна и её не стоит учитывать в расчётах.

Геометрия угловой точки
Входными данными для задачи построения сечения являются:
- геометрия угловой точки:
- размерность сетки;
- массив COORD;
- массив ZCORN;
- массив ACTNUM;
- коэффициенты общего уравнения секущей плоскости:
Решение не обязательно должно быть точным, ведь решение будет оцениваться пользователем только визуально. На выходе должны получиться массивы:
- Упорядоченный массив троек индексов (i, j, k) пересечённых ячеек;
- Упорядоченный массив координат точек полигонов пересечения ячеек;
- Упорядоченный массив индексов точек начала нового полигона в массиве координат точек пересечения. В конце массива для удобства должно быть добавлено общее количество точек пересечения.
Такой формат выбран потому, что он удобен и для визуализации через векторные графические движки, и для визуализации через триангуляционные движки.
Хорошо бы, чтобы алгоритм построения пересечения был нетребователен к памяти, так как сами сетки довольно объёмны. Например, большая сетка на 1000х1000х1000 ячеек, построенная на типе данных одинарной точности (float) занимает примерно 30 гигабайт памяти.
Нами был разработан довольно экономный к памяти алгоритм построения пересечения геометрии угловой точки и плоскости:
1. Проход по всем ячейкам и определение факта пересечение плоскости с ячейкой:
a. Подстановка каждой вершины в левую часть уравнения плоскости.
b. Если среди полученных чисел есть хотя бы два с противоположными знаками, то пересечение есть.
c. Если среди полученных чисел есть хотя бы три нуля, то пересечение есть.
d. Запись в массив флагов факта пересечения.

Геометрия угловой точки, секущая плоскость, пересечённые ячейки
2. Stream Compaction: из массива флагов собираем индексы ячеек, которые пересекаются с плоскостью. Располагаем их в новом массиве компактно.
3. Для каждой пересекаемой ячейки определяем количество точек пересечения – проход по всем вершинам и всем рёбрам ячейки. Складываем значения количества точек пересечения соответственно индексам ячеек в общий массив количества точек пересечения.
4. Prefix sum: префиксная сумма по массиву количества точек пересечения в ячейках. Это позволит определить смещение от начала массива координат точек для каждой ячейки.
5. Поиск и запись точек пересечения в массив координат точек пересечения.
6. Для каждой пересечённой ячейки находим барицентр точек пересечения. Составляем вектора по каждой точке пересечения и барицентру. Сортируем точки пересечения по углу относительно первого вектора, тем самым упорядочиваем точки в полигон.

Упорядочивание точек пересечения для одной ячейки в полигон
Таким образом получаем результирующие массивы координат полигонов и индексов начальных точек полигонов.

Результат пересечения геометрии угловой точки и плоскости
Видно, что каждый шаг алгоритма можно распараллелить.
Была создана реализация алгоритма, распараллеленная на потоки с помощью OpenMP. В такой реализации примерно 87% времени выполнения занимает первый пункт алгоритма – проход по всем ячейкам и определение факта пересечения. Время выполнения реализации на OpenMP оказалось слишком большим для комфортной работы с пересечениями в окнах визуализации.
Чтобы ускорить построение пересечения, алгоритм был реализован на CUDA. Сетка должна быть постоянно в видеопамяти, т. к. пересылка её с оперативной памяти занимает слишком много времени, даже если использовать CUDA Streams. В такой реализации примерно 43% времени выполнения занимает первый пункт алгоритма, 20% времени – пересылка результатов с видеопамяти в оперативную память. Kernel-функция, используемая в реализации для определения факта пересечения, довольно проста:
Заголовок спойлера
__global__ void checkIntersectCell (
const TCOORD* coord,
const TZCORN* zcorn,
const TACTNUM* actnum,
TFLAGS* flags,
TIJK I, TIJK J, TIJK K,
TPLANE A, TPLANE B, TPLANE C, TPLANE D,
const TCOEF* coefX, // предрасчитанные коэффициенты для поиска координат x узлов
const TCOEF* coefY // предрасчитанные коэффициенты для поиска координат y узлов
)
{
const auto globalIndex = blockDim.x * blockIdx.x + threadIdx.x;
if (globalIndex < (I * J * K))
{
if (actnum[globalIndex])
{
// globalIndex = K * J * i + K * j + k = K * (J * i + j) + k
const auto k = globalIndex % K;
const auto j = (globalIndex / K) % J;
const auto i = (globalIndex / K) / J;
int_fast8_t signPlus = 0;
int_fast8_t signMinus = 0;
int_fast8_t signZero = 0;
for (size_t p = 0; p < vertexCount; ++p)
{
const auto indexPillar = (J + 1) * (i + p / 4) + (j + (p / 2) % 2);
const auto zPillarTop = coord[6 * indexPillar + 2];
const auto z = zcorn[(2 * i + p / 4) * 2 * 2 * J * K + (2 * j + (p / 2) % 2) * 2 * K + (2 * k + p % 2)];
const auto x = (z - zPillarTop) * coefX[indexPillar] + coord[6 * indexPillar + 0];
const auto y = (z - zPillarTop) * coefY[indexPillar] + coord[6 * indexPillar + 1];
switch (sign<int_fast8_t>(A * x + B * y + C * z + D))
{
case -1: ++signMinus; break;
case 1: ++signPlus; break;
case 0: ++signZero; break;
}
}
flags[globalIndex] = static_cast<TFLAGS>((signMinus > 0 && signPlus > 0) || signZero >= 3);
}
else
{
flags[globalIndex] = static_cast<TFLAGS>(0);
}
}
}
Для тестирования был взят случай, который даёт большое количество полигонов пересечения. Сетка в тестах состояла из прямоугольных параллелепипедов, по каждому направлению (x, y и z) сетка располагалась от 0 м до 100 м. Плоскость проходила через «центр» сетки и имела нормаль (1, 1, 1).

Геометрия угловой точки и секущая плоскость для тестирования
Результаты тестирования и замеры времени выполнения представлены ниже. Тестирование проводилось на одном и том же компьютере.

Таблица с результатами тестирования и замерами времени выполнения

Синяя диаграмма показывает ускорение построения пересечения на OpenMP на 8 потоках относительно OpenMP на 1 потоке. Зелёная диаграмма показывает ускорение построения пересечения на CUDA относительно OpenMP на 8 потоках
Из результатов замеров времени выполнения видно, что, используя реализацию на CUDA, можно добиться практически незамедлительного построения пересечения больших сеток. А учитывая то, что CUDA и OpenGL функционально совместимы, то результат построения можно не пересылать с видеопамяти в оперативную память, что ускорит время решения задачи примерно на 20%.
Также видно, что количество вершин в результате пересечения незначительно отличается. Это происходит в случае, когда плоскость касается угла ячейки. Из-за точности расчётов в результате может засчитаться в пересечение очень маленький треугольник, а может и быть пропущен. Результат различается не только между построением на CPU и GPU, но также и между построением на различных CPU и на различных GPU.
Пересечение геометрии угловой точки и плоскости обычно просматривают в 3D окне.

Модель месторождения и секущая плоскость

Результат пересечения модели месторождения и плоскости
Заключение: в статье показан пример решения одной из многих задач, возникающих при создании программного обеспечения для процессов моделирования месторождений нефти и газа. Несмотря на огромный парк open-source кодов, решение подобных задач требует мультидисциплинарной подготовки разработчиков, и поэтому представляется интересными развивающими вызовами в области computer science, в которых доля рутинного программирования минимальна, а мозги надо включать «на полную». Этим и интересны задачи нашей предметной области, к которым хотелось бы привлечь внимание аудитории и потенциально заинтересованных энтузиастов и разработчиков. В частности, создание построителя пересечения геометрии угловой точки и плоскости являлось задачей на одном из хакатонов, проведённых в 2019 году «РН-БашНИПИнефть» при участии Уфимского Государственного Авиационного Технического Университета (УГАТУ).
Стоит отметить, что результатом 12-часовой работы команд оказались не полностью доработанные и не до конца оптимизированные решения: основной трудностью стало упорядочивание точек пересечения ячейки в полигон, также команды добавляли каждый новый полигон в конец контейнера координат точек, что не поддавалось распараллеливанию.
P. S. Возможно, поиск пересекаемых ячеек был бы быстрее, если бы применялось K-d дерево. Но реализовать такое решение гораздо сложнее, учитывая, что нужно придумать, как удачно построить само дерево поиска и равномерно распараллелить поиск на потоки. К тому же, если даже теоретически поиск ускорить так, чтобы он вообще не занимал времени (сейчас занимает 87% времени), то производительность на OpenMP реализации вырастет в 7.7 раз, что всё равно медленнее, чем реализация на CUDA.





