Перевод подготовлен в рамках курса "Machine Learning. Professional".
Также приглашаем всех желающих принять участие в двухдневном онлайн-интенсиве «Деплой ML модели: от грязного кода в ноутбуке к рабочему сервису».
Ошибки наблюдения и различия в подгруппах вызывают статистические парадоксы
Ошибки наблюдения и различия в подгруппах могут легко привести к статистическим парадоксам в любом прикладном решении data science. Игнорирование этих элементов может полностью дискредитировать заключения нашего анализа.
Действительно, не так уж и редко можно наблюдать такие удивительные явления, как тенденции подгрупп, которые полностью изменяются в противоположную сторону в агрегированных данных. В этой статье мы рассмотрим топ 3 наиболее распространенных статистических парадокса, встречающихся в Data Science.
1. Парадокс Берксона
Первым ярчайшим примером является обратная корреляция между степенью тяжести заболевания COVID-19 и курением сигарет (см., например, обзор Европейской комиссии Wenzel 2020). Курение сигарет — широко известный фактор риска респираторных заболеваний, так как же объяснить это противоречие?
Работа Griffith 2020, недавно опубликованная в Nature, предполагает, что это может быть случай ошибки коллайдера (Collider Bias), также называемой парадоксом Берксона. Чтобы понять этот парадокс, давайте рассмотрим следующую графическую модель, в которую мы включили третью случайную переменную: «госпитализация».
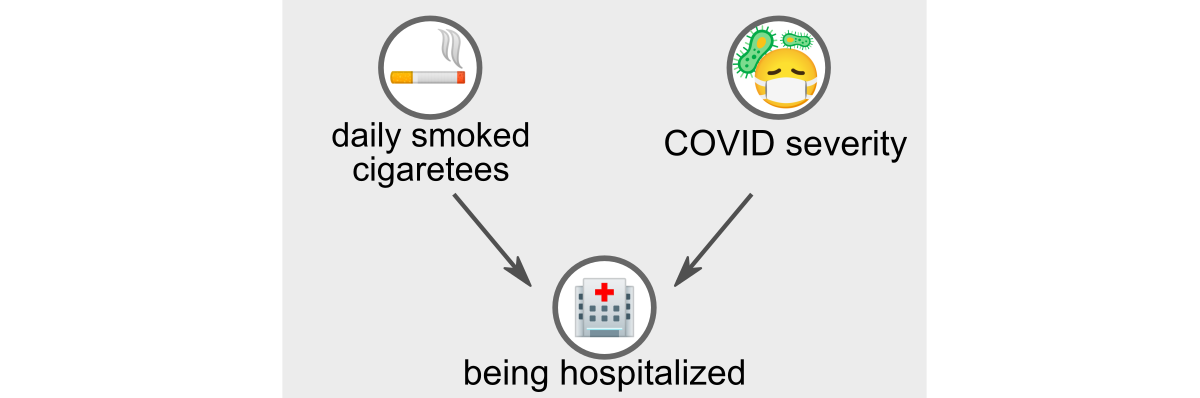
Парадокс Берксона: «госпитализация» — это переменная-коллайдер для «курения сигарет», и для «тяжести течения COVID-19». (Изображение автора)
Третья переменная «госпитализация» является коллайдером первых двух. Это означает, что курение сигарет и тяжелая форма COVID-19 увеличивают шансы попасть в больницу. Парадокс Берксона возникает в момент, когда мы принимаем за условие коллайдер, то есть когда мы наблюдаем данные только госпитализированных людей, а не всего населения в целом.
Давайте рассмотрим следующий пример набора данных. На левом рисунке у нас есть данные по всему населению, а на правом рисунке мы рассматриваем только подмножество госпитализированных людей (то есть мы используем переменную-коллайдер).
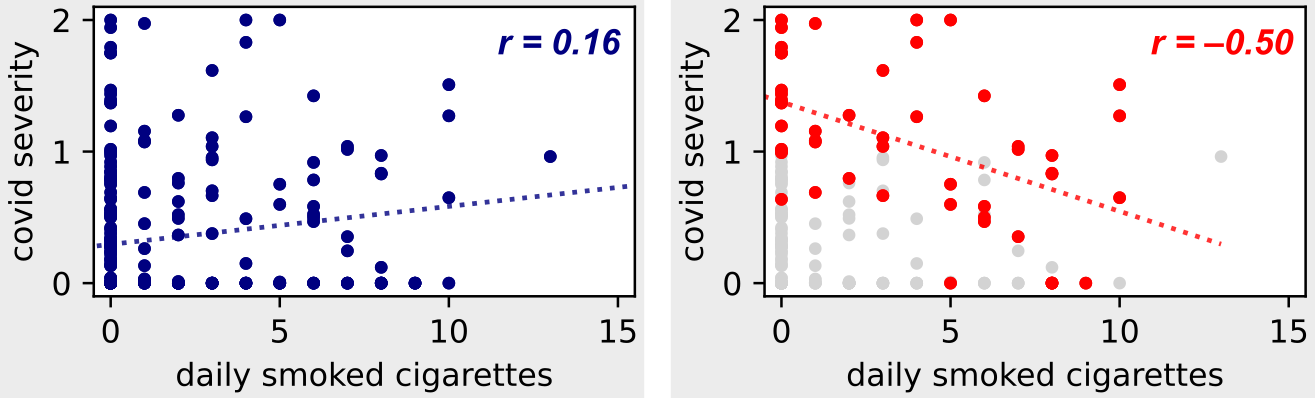
Парадокс Берксона: если мы добавим условие в соответствии с коллайдером «госпитализация», мы увидим обратную связь между курением и COVID-19! (Изображение автора)
На левом рисунке мы можем наблюдать прямую корреляцию между осложнениями от COVID-19 и курением сигарет, которую мы ожидали, поскольку мы знаем, что курение является фактором риска респираторных заболеваний.
Но на правом рисунке — где мы рассматриваем только пациентов больниц — мы видим противоположную тенденцию! Чтобы понять это, обратите внимание на следующие моменты.
1.Тяжелая форма COVID-19 увеличивает шансы на госпитализацию. То есть, если степень тяжести заболевания выше 1, то требуется госпитализация.
2. Выкуривание нескольких сигарет в день является основным фактором риска различных заболеваний (сердечно-сосудистых заболеваний, рака, диабета), которые по какой-либо причине повышают вероятность госпитализации.
3. Таким образом, если у пациента легкая форма COVID-19, он имеет больше шансов оказаться курильщиком! Более того, в отличие от COVID-19 причиной для госпитализации станет наличие у пациента какого-либо заболевания, которое может быть вызвано курением (например, сердечно-сосудистые заболевания, рак, диабет).
Этот пример очень похож на оригинальную работу Berkson 1946, где автор заметил отрицательную корреляцию между холециститом и диабетом у пациентов больниц, несмотря на то, что диабет является фактором риска холецистита.
2. Скрытые (латентные) переменные
Наличие скрытой переменной может также вызвать видимость обратной корреляции между двумя переменными. В то время как парадокс Берксона возникает из-за использования условия-коллайдера (чего, следовательно, следует избегать), этот тип парадокса можно исправить, приняв за условие скрытую переменную.
Рассмотрим, например, соотношение между количеством пожарных, задействованных для тушения пожара, и количеством людей, пострадавших в его результате. Мы ожидаем, что увеличение количества пожарных улучшит результат (в какой то степени — см. закон Брукса), однако в агрегированных данных наблюдается прямая корреляция: чем больше пожарных задействовано, тем выше число раненых!
Чтобы понять этот парадокс, рассмотрим следующую графическую модель. Ключевым моментом является повторное рассмотрение третьей случайной переменной: «степень тяжести пожара».

Парадокс скрытой переменной: «степень тяжести пожара» — это скрытая переменная для «n задействованных пожарных» и для «n пострадавших». (Изображение автора)
Третья скрытая переменная прямо пропорционально коррелирует с двумя другими. Действительно, более серьезные пожары, как правило, приводят к большему количеству травм, и в то же время для тушения требуются большое количество пожарных.
Давайте рассмотрим следующий пример с набором данных. На левом рисунке у нас отражены общие данные по всем видам пожаров, а на правом рисунке мы рассматриваем только сведения, соответствующие трем фиксированным степеням тяжести пожара (т.е. мы обусловливаем наши данные наблюдений скрытой переменной).
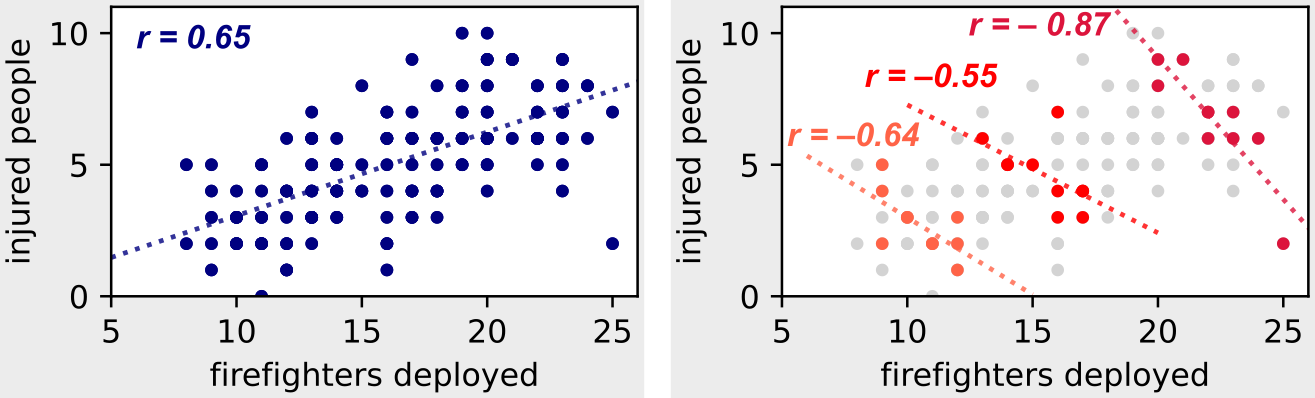
Скрытые переменные: если мы примем за условие скрытую переменную «степень тяжести пожара», мы увидим обратную корреляцию между количеством задействованных пожарных и количеством раненых! (Изображение автора)
На правом рисунке, где мы берем за условие для данных наблюдения степень тяжести пожара, мы видим обратную корреляцию, которую мы ожидали.
При заданной степени тяжести пожара мы действительно видим, что чем больше задействовано пожарных, тем меньше травм у людей.
Если мы посмотрим на пожары высокой степени тяжести, мы увидим ту же тенденцию, даже несмотря на то, что количество задействованных пожарных и количество травм увеличиваются.
3. Парадокс Симпсона
Парадокс Симпсона — это удивительное явление, когда мы постоянно наблюдаем какую-то тенденцию возникающую в подгруппах, и которая меняется на противоположную, если эти подгруппы объединить. Часто это связано с несбалансированностью классов в подгруппах данных.
Нашумевший случай этого парадокса произошел в 1975 году, когда Бикелем были проанализированы показатели приема абитуриентов в Калифорнийский университет, чтобы найти доказательства дискриминации по половому признаку, и были выявлены два явно противоречащих друг другу факта.
С одной стороны, он заметил, что на каждом факультете число принятых абитуриентов женского пола выше, чем абитуриентов мужского пола.
С другой стороны, общий процент приема среди абитуриентов женского пола был ниже, чем у абитуриентов мужского пола.
Чтобы понять, как как такое может быть, давайте рассмотрим следующий набор данных с двумя факультетами: Факультет A и Факультет B.
Из 100 абитуриентов мужского пола: 80 подали заявки на Факультет A, из которых 68 были приняты (85%), а 20 подали заявки на Факультет В, из которых приняты были 12 человек (60%).
Из 100 абитуриентов женского пола: 30 подали заявки на Факультет А, из которых 28 были приняты (93%), в то время как 70 подали заявки на Факультет B, из которых были приняты 46 (66%).
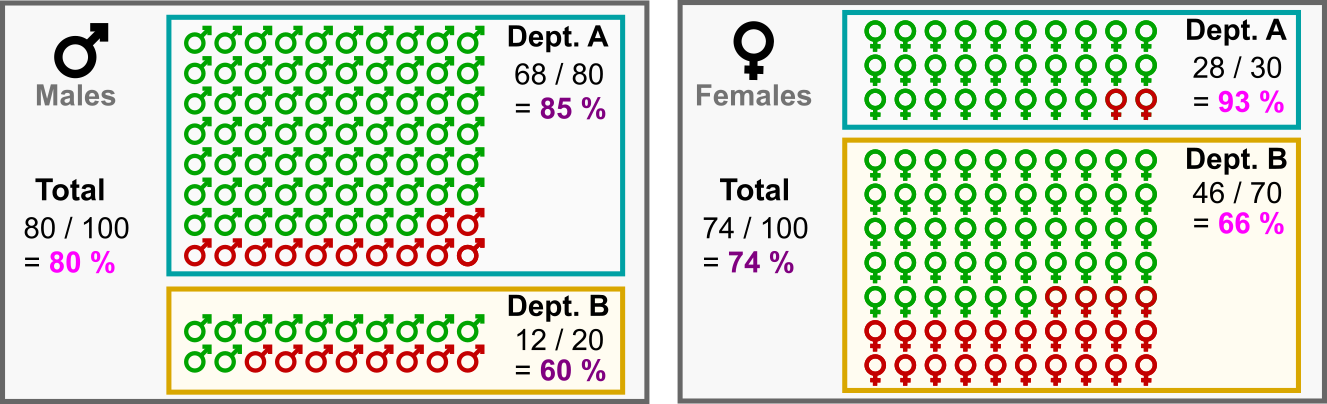
Парадокс Симпсона: женщины-абитуриенты с большей вероятностью будут приняты в каждом факультете, но общий процент приема женщин в сравнении с мужчинами ниже! (Изображение автора)
Парадокс выражается следующими неравенствами.

Парадокс Симпсона: неравенство, лежащее в основе очевидного противоречия. (Изображение автора)
Теперь мы можем понять происхождение наших, казалось бы, противоречивых наблюдений. Дело в том, что существует ощутимый классовый гендерный дисбаланс среди абитуриентов на каждом из двух факультетов (Факультет A: 80–30, Факультет B: 20–70). Действительно, большинство студентов женского пола подали заявку на более конкурентный Факультет B (который имеет низкие показатели приема), в то время как большинство студентов мужского пола подали документы на менее конкурентный Факультет А (который имеет более высокие показатели приема). Это обусловливает противоречивые данные, которые мы получили.
Заключение
Скрытые переменные, переменные-коллайдеры, и дисбаланс классов могут легко привести к статистическим парадоксам во многих практических моментах data science. Поэтому этим ключевым моментам необходимо уделять особое внимание для правильного определения тенденций и анализа результатов.
Узнать подробнее о курсе "Machine Learning. Professional"
Участвовать в онлайн-интенсиве «Деплой ML модели: от грязного кода в ноутбуке к рабочему сервису»





