Топология и комплексный анализ для ничего не подозревающего разработчика игр: сжатие единичных 3D-векторов

Как вы уже могли понять из моих предыдущих статей, мне нравится использовать разработку игр как оправдание для демонстрации сложной математики, для которой в противном случае у большинства людей не было бы применения. И эта статья не исключение! Я хочу показать очень крутую технику, соответствующую любопытным для меня пунктам:

• процесс достаточно нагляден
• он намного быстрее, чем обычная техника, выполняющая ту же задачу
• он использует очень необычное свойство представления вещественных чисел в формате с плавающей запятой, что подразумевает, что...
• он не работает в классическом анализе. Чтобы этот алгоритм работал в теории, нужно попасть в удивительный мир неклассической математики! И если уж это не разбудило ваше любопытство, то я уж и не знаю, что ещё поделать.

Эта статья довольно длинная и теоретическая, потому что она требует глубоко изучить объяснения, так что не торопитесь и перечитывайте те части, которые показались вам не столь очевидными с первого раза.

Немного о контексте (GPU)

Один из важных аспектов, на который стоит обращать внимание в разработке игр, а в более широком смысле — и в любой области с активным использованием графики — это пропускная способность GPU. Центральный процессор и GPU — отдельные физические устройства, и для обмена данными им требуется синхронизация. Если вы уже занимались параллельной обработкой, то знаете, что когда двум устройствам нужно синхронизироваться, это означает потерю значительного количества времени. Взаимодействие CPU-GPU в этом плане ничем не отличается, поэтому мы стремимся минимизировать передачу данных, как в количестве операций, так и в объёме передаваемых данных.

Минимизация количества операций передачи данных обычно выполняется при помощи буферизации: мы стремимся уместить все данные в как можно меньшее количество массивов, а затем передаём всё за один раз, чтобы больше не нужно было о них волноваться. Минимизация объёма данных в операциях передачи — совершенно другая тема, и решения этой задачи почти всегда индивидуальны. В качестве крайнего примера этого можно посмотреть, как движку рендеринга Destiny удаётся уместить позицию, нормали поверхности, флаги материалов и полные анизотропные BSDF-параметры в 96 бит, т.е. в три числа с плавающей запятой (стр. 62 и дальше). Однако хороших результатов можно добиться и общими методами, к которым потом добавляются индивидуальные решения для оптимизации.

Сегодня мы обсудим сжатие без потерь отдельных единичных 3D-векторов. В этом предложении содержится несколько ключевых слов:

• Единичные 3D-векторы: 3D-векторы, имеющие длину 1
• сжатие без потерь: уменьшение размера описания единичных 3D-векторов без потерь точности. Это противоположно сжатию с потерями
• отдельных: кодирование и декодирование вектора выполняется без информации о его соседях. Если бы ситуация была обратной, то это могло бы быть что-то вроде пакетного сжатия, при котором сжимаются не отдельные векторы, а их массивы

Прежде чем двигаться дальше, я должен упомянуть превосходную статью “A Survey of Efficient Representations for Independent Unit Vectors” авторов Cigolle, Donow, Evangelakos, Mara, McGuire и Meyer, из которой я черпал вдохновение для своего поста. Сразу должен сказать, что алгоритм, о котором я расскажу, менее эффективен, чем представленный в статье алгоритм oct. Если вы стремитесь в максимальной эффективности, то прочитайте статью и используйте oct. Цель моего поста — показать красоту использования очень необычной математики, создав при этом, как мы увидим позже, очень удобный алгоритм.

Топология прямо в вашей видеоигре

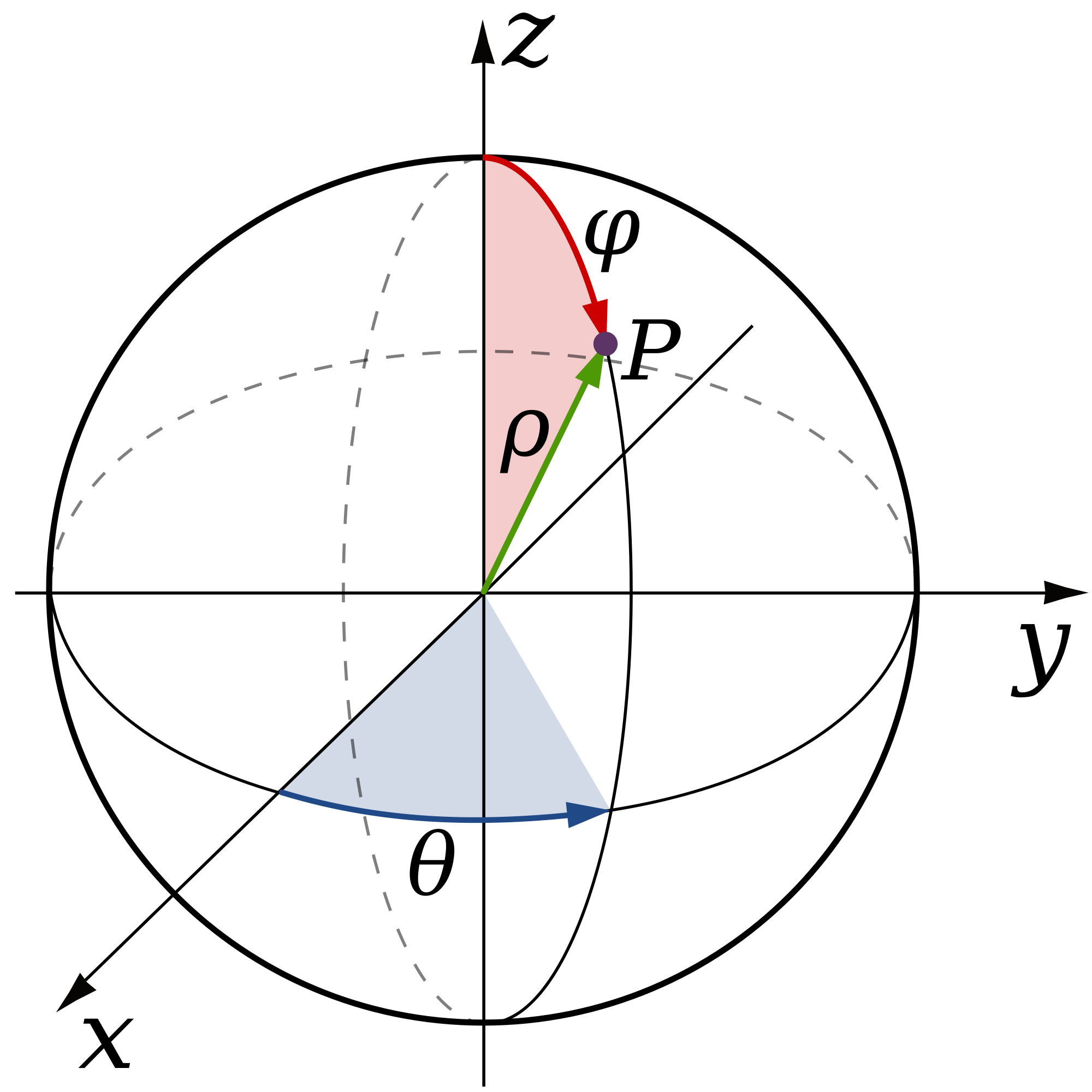
В случае единичной сферы важны только θ и φ, потому что ρ всегда равно 1, а потому избыточно.

Отправной точкой алгоритма является наблюдение о том, что единичные 3D-векторы эквивалентны точкам на сфере. Как вы вероятно знаете, сфера — это двухмерная поверхность, то есть для уникальной идентификации точек на сфере требуется всего две координаты. Очень распространённым примером этого являются сферические координаты, при которых точка на сфере задаётся двумя углами, θ и φ.

Интересно, что довольно неприятное свойство заключается в том, что хотя и сфера, и заполненный квадрат (одно возможное пространство для 2D-координат) являются 2D-объектами, между ними на самом деле нет соответствия. Это означает, что не существует способа привязать уникальную точку на сфере к каждой уникальной точке квадрата (по крайней мере, непрерывным образом); говорится, что они негомеоморфны (проще говоря, у одного есть граница, а у другого нет). Неприятным результатом этого становится то, что некоторые 2D-координаты теряются в том смысле, что разные координаты соответствуют одинаковых точкам на сфере (например, в случае сферических координат, когда φ равен 0, соответствующая точка будет северным полюсом, вне зависимости от координаты θ). С точки зрения сжатия мы теряем ценные битовые паттерны, которыми мы могли бы описать точки сферы!

Если вам хочется больше математики и вы желаете доказать, что квадрат и сфера негомеоморфны, то можно воспользоваться тем фактом, что сфера в отличие от квадрата не стягиваема, а стягиваемость является топологическим свойством; так же для доказательства можно использовать теорему Борсука-Улама. Ещё мне говорили, что в доказательстве могут помочь гомотопические группы, но это уже находится за пределами моей области знаний.

Однако эта проблема возникает не только со сферическими координатами; от неё будет страдать любое непрерывное 2D-представление точек сферы. Тем не менее, запомните это на будущее.

Сферические координаты обладают также и другими плохими свойствами:

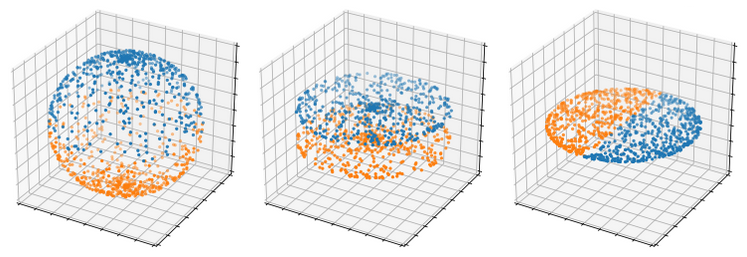
• Они имеют плохое распределение по сфере. Если сгенерировать случайные сферические координаты и преобразовать их обратно в 3D-точки, они образуют скопления вокруг полюсов и будут довольно разреженными возле экватора. Это является следствием того, что 3D-векторы рядом с экватором будут менее точно различимы.
  
  
  
  
  Распределение на сфере 10 000 равномерно распределённых сферических координат
• Их упаковка и распаковка затратны. Для упаковки (3D → 2D) требуется одна операция acos и одна atan2, которые являются довольно затратными обратными тригонометрическими функциями, а для распаковки (2D → 3D) требуются две операции cos и две операции sin, которые тоже далеко не экономны.

Изучите упомянутую выше статью, чтобы узнать о других сравнениях сферических координат и иных способов сжатия.

Задача сохранения битовых паттернов… и скорости

Способ, который мы рассмотрим, имеет большое преимущество — его вычисление гораздо быстрее, более чем в два раза, чем неоптимизированный наивный бенчмарк (протестировано на упаковке и распаковке 10 миллионов случайных векторов на C++ в Visual Studio 19 на Intel Core i5 7th gen). Кроме того, способ не имеет сингулярности, то есть каждая упакованная точка соответствует единственной распакованной точке, в отличие от упомянутых выше сферических координат.

Как говорилось ранее, между единичной сферой и единичным квадратом нет гомеоморфизма, то есть мы не можем должным образом привязать каждую уникальную точку в квадрате к другой уникальной точке на сфере. Но давайте рассмотрим следующие построения — пока нас будет волновать только северная полусфера, в которой находятся точки с положительной или нулевой координатой Z.


Мы «сплюснули» северную полусферу в диск, отбросив координату Z каждой точки (или присвоив ей значение 0).

Мы нашли способ привязать каждую точку северной полусферы к каждой точке единичного диска. Несколько примечательных точек:

• северный полюс попадает в (0, 0).
• каждая точка на границе полусферы остаётся такой же. Если конкретнее, то полусфера и диск имеют одинаковую границу. Это логично, ведь точки на границе полусферы имеют Z = 0, то есть отбрасывая координату Z, мы ничего не меняем.

Сжатие диска: простая комплексная задача

Следующее построение требует небольшого введения. На всякий случай скажу, что комплексные числа — это расширение пространства вещественных чисел (обычных чисел наподобие 0, 1, 129,43, пи, 335/117, квадратного корня 2, и так далее), в котором используется особое число i, называемое мнимой единицей. Комплексные числа имеют вид a + ib, где a и b — некие вещественные числа (соответственно, вещественная и мнимая части), а i имеет свойство i² = -1. Это позволяет нам сопоставить комплексные числа с точками на 2D-плоскости. Если взять за z комплексное число вида z = a + ib, то можно представить z точкой с координатами (a, b) на плоскости. Функции извлечения «вещественной части» и «мнимой части» комплексного числа z обозначаются как Re(z) и Im(z).


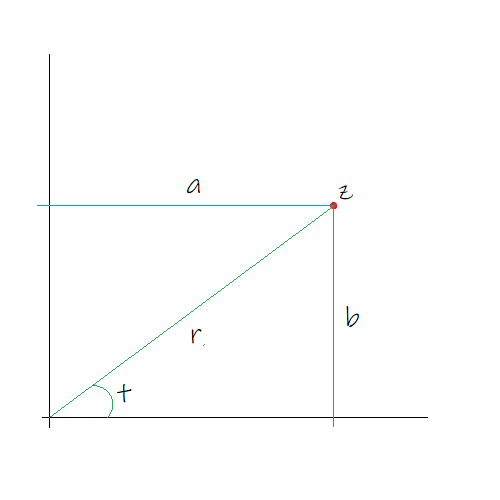
Комплексное число z и представляющие его значения.

Кроме вещественной и мнимой частей комплексного числа можно также учитывать длину и угол, образуемый им с осью X. Это называется полярным представлением. Полярная длина и полярный угол — это норма |z| и аргумент Arg(z). Удобное свойство обоих представлений заключается в том, что сложение комплексных чисел выполняется сложением вещественной и мнимой частей, а умножение комплексных чисел выполняется умножением норм и сложением аргументов.

Здесь нам интересны две операции: возведение в квадрат и получение квадратного корня комплексного числа. Возведение в квадрат комплексного числа выполняется точно так же, как и у вещественных чисел: просто умножаем его на себя, по сути возводя в квадрат норму и удваивая аргумент. Учтите, что если норма комплексного числа меньше 1, то при возведении в квадрат её длина останется меньше единицы; таким образом, если взять каждое комплексное число на диске, имеющее положительную вещественную часть, и возвести их всех в квадрат, то мы по сути получим в результате весь диск.


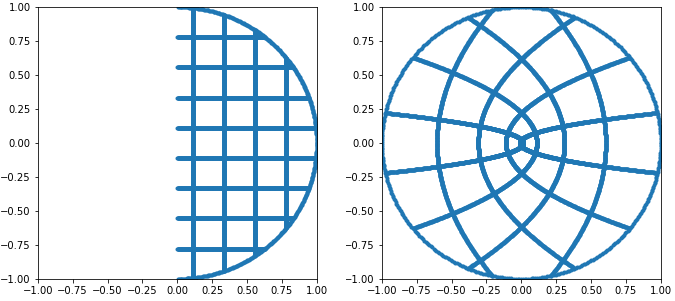
Слева показано несколько комплексных чисел в половине диска с положительной вещественной частью (координатой X). Справа показан результат возведения в квадрат всех этих точек. Половина диска теперь заполняет весь диск!

С «удвоением аргумента» связана одна хитрость: оно зависит от стороны оси X, на которой лежит точка. Правило показано ниже.


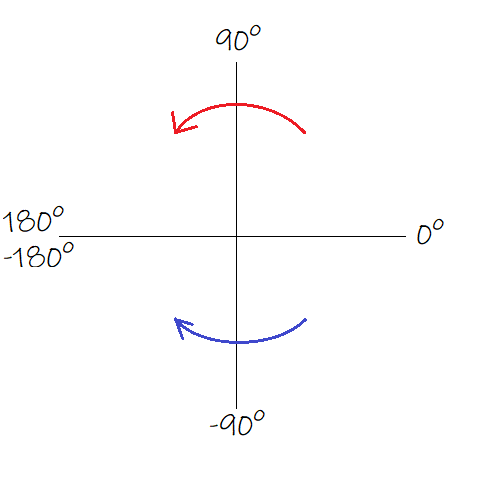
Комплексное число с положительной мнимой частью (координата Y) поворачивается влево, а комплексное число с отрицательной мнимой частью (координата Y) поворачивается вправо.

Как и в случае с вещественными числами, квадратный корень — это операция, обратная возведению в квадрат: для заданного комплексного числа z, квадратными корнями (их два) являются числа c, такие, что c² = z. Как и в случае с вещественными числами, если c — квадратный корень z, тогда -c тоже им является. То из чисел c и -c, аргумент которого равен половине аргумента z, называется главным значением квадратного корня (это схоже со взятием положительного квадратного корня вещественного числа вместо отрицательного квадратного корня).

Если вы понимаете, что при возведении в квадрат комплексного числа возводится в квадрат его норма и удваивается его аргумент, то легко догадаетесь, что главное значение квадратного корня берёт квадратный корень из нормы и делит пополам аргумент (следуя показанному выше правилу, но с перевёрнутыми стрелками). Как и в случае с возведением в квадрат, при взятии квадратного корня комплексного числа с нормой меньше 1 норма остаётся меньше 1; следовательно, это «сжимает» единичный диск в его половину положительных вещественных чисел.


Слева показано несколько точек на единичном диске. Справа показан результат взятия квадратного корня всех этих точек. Весь диск теперь умещается в половину самого себя!

В этом и заключается основа алгоритма: по сути, мы сжимаем весь единичный диск в одну его половину — в половину с положительной вещественной частью. Как вы помните, недавно мы сплющили верхнюю половину сферы в единичный диск; теперь стоит посмотреть, что мы с этим будем делать.

Соединяем всё вместе

Давайте суммируем то, что только что сделали: мы сплющили половину сферы в один единичный диск, отбросив координату Z всех его точек, и сжали единичный диск в его собственную половину с положительной вещественной частью при помощи комплексного главного значения квадратного корня. По сути, мы сплюснули половину сферы в половину диска! Теперь с небольшими изменениями мы можем сделать то же самое для сжатия оставшейся половины сферы в оставшуюся половину диска.

Нижняя половина сферы (все точки сферы с отрицательной координатой Z) аналогично сплющиваются в единичный диск повторным отбрасыванием координат Z. Однако для всех комплексных чисел z в диске мы берём значение, противоположное главному квадратному корню z (т.е. мы берём -c вместо c). Так как главное значение квадратного корня всегда имеет положительную вещественную часть, противоположное ему значение всегда будет иметь отрицательную вещественную часть; по сути, мы сплющили оставшуюся половину сферы в оставшуюся половину диска, и на этом этап сжатия завершён!


Полный этап сжатия. Заметьте, что северная и южная полусферы (синяя и оранжевая) сплюснуты в две копии единичного диска, а затем ужаты в две половины одного единичного диска.

Алгоритм сжатия выглядит следующим образом:

function packUnitVector(unit)
    disk = new Complex(unit.x, unit.y)
    packed = principalSquareRoot(disk)
    return unit.z < 0 ? -packed : packed

И вот так, всего в трёх строках псевдокода, мы применили всю рассмотренную нами теорию для создания эффективного алгоритма. Если в вашей среде нет формулы главного значения квадратного корня, то её можно найти в Википедии (особое внимание следует уделить выбору знака мнимой части). Вот справочная реализация на C++, которую я использую в своём коде:

// Principal complex square root of 'x + iy'
float2 csqrt(float x, float y)
{
    float r = sqrt(x * x + y * y);
    return float2(sqrt((r + x) / 2), (y < 0 ? -1 : 1) * sqrt((r - x) / 2));
}

Возвращаемся обратно

Мы справились со сжатием, теперь приступим к распаковке.

Распаковка заключается в обратном порядке выполнения всех шагов сжатия:

• разворачиваем и положительную, и отрицательную половины вещественных частей единичного диска в два полных диска
• сопоставляем каждый полный диск с соответствующей ему полусферой

Если вкратце, то мы начинаем с упакованного значения p, возводим его в квадрат, чтобы вернуться к точке на диске, получаемой из одной из полусфер, а затем используем знак Re(p), чтобы выяснить, из какой полусферы взята точка в диске. При помощи уравнения x² + y² + z² = 1, задающего точки на единичной сфере, мы можем воссоздать отсутствующую координату Z упакованной точки.

Следует учесть, что вычисление квадрата упакованного значения всегда будет давать нам правильную точку диска вне зависимости от её исходной полусферы (верхней или нижней), потому что z² = (-z)².

Алгоритм распаковки имеет следующий вид:

function unpackUnitVector(packed):
    disk = packed * packed
    unit = new Vec3()
    unit.x = disk.real()
    unit.y = disk.imag()
    unit.z = sqrt(1 - unit.x * unit.x - unit.y * unit.y) * (packed.real() < 0 ? -1 : 1)
    return unit

И таким образом мы получили алгоритм, очень эффективно создающий 2D-представление единичных 3D-векторов, который в отличие от сферических координат, не теряет никаких битовых паттернов и не имеет сингулярности. Если не учитывать пару хитростей оптимизации, позволяющих ускорить вычисления, это практически готовая версия алгоритма.

… или нет? Если вы следили внимательно, то заметили, что здесь что-то не так. Я сказал, что сфера и единичный квадрат негомеоморфны, и тем не менее каким-то образом смог привязать уникальную точку в диске к каждой уникальной точке на сфере? Кроме того, мы пока не упоминали никакой неклассической математики, так что же происходит?

И в самом деле, наш алгоритм имеет серьёзный недостаток: он работает для каждой точки всей сферы, за исключением точек на северной полусфере с Y = 0 и X <= 0, которые при упаковке и распаковке ошибочно сопоставляются с соответствующей точкой на северной полусфере.

Причина этого заключается в том, что при отбрасывании их координаты Z соответствующее комплексное число является отрицательным вещественным числом, оно не имеет мнимой части. Когда мы берём главное значение квадратного корня отрицательного вещественного числа, то в свою очередь получаем полностью мнимое комплексное число, которое не имеет вещественной части (это схоже с тем, что главное значение квадратного корня -1 равно i). Затем мы пытаемся сохранить знак координаты Z в том, что по сути является нулём.


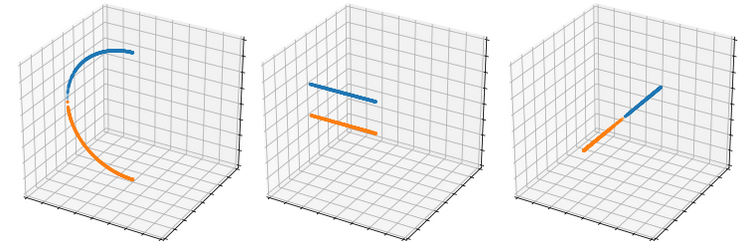
Проблемная полоса. Точки с Y = 0 и X <= 0 упаковываются в линию чисто мнимых чисел с неопределимыми вещественными частями.

Давайте посмотрим, что происходит, когда мы упаковываем две такие точки (не забывайте, что x <= 0).

       | North point | South point
 unit  | (x, 0, z)   | (x, 0, -z)
 disk  | x + 0i      | x + 0i
packed | 0 + √(-x)i  | -0 - √(-x)i

Так как мнимая часть проекции на диск обеих точек равна нулю, мы не можем хранить знак координаты Z в знаке вещественной части главного значения квадратного корня, потому что она сама равна нулю. Мы можем просто остановиться на этом, приняв тот факт, что алгоритм не работает для этих точек — или можем двинуться дальше.

Забываем то, чему научились

В каждой известной мне области и ветви математики принимается, что 0 = -0. Это следует из определения -a, противоположного элементу a, гласящего, что "-a — это единственное число, дающее 0 при суммировании с a". Так как 0 является также нулевым элементом относительно сложения (0 +a = a + 0 = a), то единственное, что нужно прибавить к 0, чтобы получить 0 — это сам 0.

Однако в разработке ПО всё по-другому. В большинстве представлений чисел с плавающей запятой наряду с экспонентом и мантиссой используется дополнительный бит для хранения знака. Это означает, что когда экспонент и мантисса равны 0, то знаковый бит можно использовать для различения положительного и отрицательного нулей. В большинстве языков программирования (если не во всех) оба этих нуля обрабатываются как один единственный ноль (просто попробуйте выполнить 0 == -0), но разница существует, и это можно увидеть, если попробовать вывести в терминал “-0” и “0” — именно так они и выведутся.

Для нас это чрезвычайно важно: значение нуля на самом деле можно использовать для хранения информации о знаке! На самом деле, она и так хранится правильно; в нашем случае проблема заключается в том, что она считывается неверно. Если посмотреть на предпоследнюю строку в алгоритме распаковки, то мы увидим следующее:

packed.real() < 0 ? -1 : 1

Эта операция считывает знак вещественной части упакованного значения, чтобы определить, к какой полусфере принадлежит точка — к северной или южной. Однако в случае, когда packed.real() равно 0 или -0, знак игнорируется оператором сравнения и тернарный оператор всегда возвращает 1. Правильным способом считывания знака будет настоящий запрос состояния знакового бита, например, с помощью std::signbit из C++ или np.signbit из Numpy в Python — функция зависит от языка. Помните, что знаковый бит равен 1, когда число отрицательно, и равен 0, когда число положительно.

Таким образом, мы получаем исправленную и стопроцентно работающую функцию:

function unpackUnitVector(packed):
    disk = packed * packed
    unit = new Vec3()
    unit.x = disk.real()
    unit.y = disk.imag()
    unit.z = sqrt(1 - unit.x * unit.x - unit.y * unit.y) * (signbit(packed.real()) ? -1 : 1)
    return unit

Вот и всё! Теперь алгоритм завершён. Неклассическая математика проявляется в том, что мы используем факт отличия 0 от -0, что ложно для всех известных мне областей математики. Однако существует способ сделать эту странность логичной в теоретическом, математически строгом смысле.

Пространства, которые играют не по правилам: прямая с двумя точками начала координат

Чтобы лучше понимать изложенное ниже вам стоит знать концепции классов эквивалентности и окрестностей. Это необязательно, но так будет понятнее.

Мы можем обеспечить логичность этой странности со «знаковым нулём», начав с интересного топологического пространства: прямой с двумя точками начала координат.


Прямая с двумя точками начала координат — это обычная вещественная числовая ось, которая каким-то образом отрастила себе дополнительный 0.

Прямая с двумя точками начала координат получается, когда мы берём две вещественные числовые оси и склеиваем каждое число с равным ему противоположным, за исключением 0. Формально прямая с двумя точками начала координат является факторпространством R² с отношением эквивалентности, идентифицирующим два числа, если они равны и не являются 0. Результатом становится прямая вещественных чисел с двумя разными нулями, равноудалёнными от любой точки, но одновременно отличными друг от друга. Формально любые две окрестности каждого из нулей всегда имеют непустое пересечение.

Мы можем расширить это и попробовать определить «дископодобный» объект, который использовали в этой статье. Ранее мы принудительно сохраняли знак координаты Z точки в вещественную часть главного значения квадратного корня её проекции на комплексный диск, даже если эта вещественная часть равна 0. Это значит, что мы использовали не комплексные числа, а другое, похожее на них понятие: комплексное число, мнимая часть которого является вещественным числом, а вещественная часть которого является точкой на прямой с двумя точками начала координат, поэтому мы можем отличать вещественную часть, равную +0 и -0. На самом деле мы используем комплексные числа с двумя точками начала координат!

И в самом деле, мы не нашли биекцию (взаимно однозначное отображение) между сферой и единичным диском, но нашли биекцию между сферой и единичным диском с двумя точками начала координат. Я не проверял, является ли эта биекция гомеоморфизмом (гомеоморфизм — это биекция, непрерывная обоих направлениях), но возможно, когда-нибудь этим займусь.

Немного топологии в конце

В заключение хочу подчеркнуть, что хотя использованная нами комплексная плоскость с двумя точками начала координат не следует из того же построения, что и прямая с двумя началами координат, на самом деле она является эквивалентом другой комплексной плоскости с двумя точками начала координат, построенной аналогично прямой с двумя началами координат.

В случае прямой с двумя точками начала координат мы склеили две копии вещественной числовой оси во всех местах, кроме 0. Мы можем сделать то же самое с двумя копиями комплексной плоскости, склеив вместе каждую пару равных комплексных чисел, не являющихся 0, и аналогично получить комплексную плоскость с двумя точками начала координат. Это построение отличается от построения новой комплексной плоскости из прямой с двумя точками начала координат и обычной вещественной числовой оси: первая является факторпространством, а последняя — произведением пространств. Однако единственное различие между двумя получившимися пространствами заключается в способе записи разных нулей в каждом пространстве: в первом они счтываются как (0 + 0i)a и (0 + 0i)b (два нуля, взятые из двух разных пространств, не склеенных вместе), а в последнем они считываются как (0a + 0i) и (0b + 0i). На самом деле оба пространства являются гомеоморфными, так что можно спокойно использовать одно там, где требуется другое.

Вывод

Надеюсь, вам понравился этот экскурс в мир причудливой и непонятной математики. Снова подчеркну тот факт, что, строго говоря, этот алгоритм проявляет себя хуже, чем алгоритм oct из статьи, упомянутой мной в начале. Хотя он близок или даже быстрее по времени выполнения, его распределение точек на сфере далеко не так хорошо. Я написал эту статью затем, чтобы показать, как кажущаяся инопланетной математика, похожая на абстрактную чушь, на самом деле может иметь очень интересное применение в реальном мире; более того, я нахожу эту абстрактную чушь восхитительной. Надеюсь, вы извлекли из статьи что-то полезно, спасибо за прочтение!