Треугольники, множества и алгебра

Иногда кажется, что некоторые математические темы изучены вдоль и поперек, например, треугольники. Ну что в этих треугольниках может быть нового и интересного? Тем не менее, даже такие, казалось бы, тривиальные объекты могут предстать под неожиданным углом. Давайте возьмем какую-нибудь простенькую задачку и попробуем ее решить. Постараемся найти треугольник с целочисленными сторонами, медианами и площадью. Мало ли, вдруг у нас получится.

Как перечислить все треугольники?

Даже несмотря на то, что некоторые множества содержат бесконечное количество элементов, они являются перечислимыми. Например, множество четных чисел может быть перечислено с помощью очень простого алгоритма - для любого n выдаем 2n и все. Во многом такая простота перечислимости некоторых множеств обусловлена тем, что элементы как-то упорядочены. Фактически, перечислить - значит пронумеровать, например, 2 - это первое четное число, 6 - третье. Но можем ли мы проделать то же самое с треугольниками? Если задавать треугольники с помощью кортежей вида a,b,c, то можем ли мы сказать, что треугольник 1,1,1 является первым, а треугольник 3,2,2 - четвертым или восьмым или еще каким-нибудь номером? Оказывается, можем.

Первое, что нужно придумать - это то как упорядочить множество треугольников. Первое, что приходит в голову - взять треугольник с какой-нибудь одной фиксированной стороной и выписать другие треугольники, стороны которого не меньше заданной. Например, так:

tri = []
a = 3
for b in range(a, 8):
    for c in range(b, 10):
        if a + b > c:
            tri.append([a, b, c])
tri

[[3, 3, 3],
 [3, 3, 4],
 [3, 3, 5],
 [3, 4, 4],
 [3, 4, 5],
 [3, 4, 6],
 [3, 5, 5],
 [3, 5, 6],
 [3, 5, 7],
 [3, 6, 6],
 [3, 6, 7],
 [3, 6, 8],
 [3, 7, 7],
 [3, 7, 8],
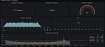
 [3, 7, 9]]

Как видим, первая сторона неизменна, а третья не превосходит суммы двух первых, на графике это будет выглядеть так:

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
from gmpy2 import is_square

fig, ax = plt.subplots(2, 1, figsize=(11, 7))
tri = np.array(tri)
x = np.r_[0: len(tri)]

ax[0].plot(x, tri[:, 1], drawstyle='steps-post')
ax[0].set_xticks(x)
ax[0].set_title('Сторона $b$')
ax[1].plot(x, tri[:, 2], drawstyle='steps-post')
ax[1].set_xticks(x)
ax[1].set_title('Сторона $c$');

Перед нами две ступенчатые функции, а значит мы можем задать стороны всех таких треугольников следующим образом:

Если заменить тройку на а на , то получим следующее:

Теперь любой треугольник можно изображать в виде точки на координатной плоскости, преобразуя стороны треугольников в координаты по двум простым формулам:

Чтобы перейти от координат к номерам достаточно воспользоваться канторовской нумерацией:

Или, если вместо координат использовать стороны треугольника:

Не знаю как вы, а я очень удивился, когда понял, что у каждого треугольника с целыми сторонами может быть свой номер. Есть что-то необычное в том, что подмножества треугольников, например, равнобедренные, могут выглядеть вот так:

isosceles_xy = []
isosceles_n = []

for x in range(1, 20):
    for y in range(1, 20):
        a = x
        b = y//x + x
        c = y + x - (x - 1)*(y//x)
        if a == b or a == c or b == c:
            n = ((x + y)*(x + y + 1))//2 + x
            isosceles_xy.append([x, y])
            isosceles_n.append(n)
        a, b, c = a**2, b**2, c**2

isosceles_xy = np.array(isosceles_xy)

fig, ax = plt.subplots(1, 2, figsize=(16, 8))

ax[0].scatter(isosceles_xy[:, 0], isosceles_xy[:, 1])
ax[0].set_xticks(np.r_[0:20])
ax[0].set_yticks(np.r_[0:20])
ax[0].set_title('Координаты равнобедренных\nтреугольника',
                fontsize=15)
ax[1].scatter(np.r_[0: len(isosceles_n)], isosceles_n)
ax[1].set_title('Номера равнобедренных\n треугольника',
                fontsize=15);

Причем тут алгебра?

Очень похоже, что номера равнобедренных треугольников представляют собой множество парабол, нарисованных на одном графике. Так и есть, каждая из них может быть задана уравнением вида:

То же самое можно сказать и про многие другие подмножества треугольников. Например, вот так будут выглядеть треугольники с целыми, четными сторонами и одной целой медианой, проведенной к стороне :

one_m_xy = []
one_m_n = []
for x in range(2, 50, 2):
    for y in range(35000):
        a = x
        b = y//x + x
        c = y + x - (x - 1)*(y//x)
        m_c = 2*(a**2 + b**2) - c**2
        if m_c%4 == 0 and is_square(m_c):
            n = ((x + y)*(x + y + 1))//2 + x
            one_m_xy.append([x, y])
            one_m_n.append(n)
            
one_m_xy = np.array(one_m_xy)

fig, ax = plt.subplots(1, 2, figsize=(16, 8))

ax[0].scatter(one_m_xy[:, 0], one_m_xy[:, 1])
ax[0].set_title('Координаты', fontsize=15)
ax[1].scatter(np.r_[0: len(one_m_n)], one_m_n)
ax[1].set_title('Номера', fontsize=15);

На графике с координатами расположено множество кубических функций вида:

Не знаю, можно ли задать функции для всех кубических функций, но некоторые из них могут быть заданы, например, так:

Можно взять какую-то отдельную из них, например при j=0 и получить следующие формулы для координат треугольников:

Используя данные координаты можем задать функции для сторон и медианы:

Мы можем попробовать провернуть то же самое для треугольников, у которых две целые медианы:

two_m_xy = []
two_m_n = []
for x in range(2, 100, 2):
    for y in range(100000):
        a = x
        b = y//x + x
        c = y + x - (x - 1)*(y//x)
        m_b = 2*(a**2 + c**2) - b**2
        m_c = 2*(a**2 + b**2) - c**2
        if m_b%4 == 0 and m_c%4 == 0 and is_square(m_b) and is_square(m_c):
            n = ((x + y)*(x + y + 1))//2 + x
            two_m_xy.append([x, y])
            two_m_n.append(n)
            
two_m_xy = np.array(two_m_xy)

fig, ax = plt.subplots(1, 2, figsize=(16, 8))
ax[0].scatter(two_m_xy[:, 0], two_m_xy[:, 1])
ax[0].set_title('Координаты', fontsize=15)
ax[1].scatter(np.r_[0: len(two_m_n)], two_m_n)
ax[1].set_title('Номера', fontsize=15);

Хоть этого и не видно на графике, но координаты треугольников с двумя целыми медианами задаются кубическими, квадратичными и линейными функциями. К сожалению, не могу привести все выкладки куда−то потерялись записи.

Если мы нарисуем график для треугольников с тремя целыми медианами, то получим следующее:

Таких треугольников очень мало, они очень сильно разрежены, но любопытно, что если найти хотя бы один такой треугольник, то все последующие могут быть заданы как:

Например, если взять треугольник 136, 170, 172 и умножить его стороны на 5, то мы снова получим треугольник с целыми сторонами и медианами.

Почему это все бесполезно?

Сначала кажется, что нумерация треугольников это шажок в сторону создания системы диофантовых уравнений, которые определяли бы стороны треугольников с целыми сторонами и медианами. Затем эти уравнения можно было бы подставить в формулу Герона и потом попытаться доказать возможность получения или неполучения треугольников с целой площадью. Но, к сожалению, нумерация треугольников абсолютно бесполезна в этом направлении. Все дело в том, что сама задача поиска треугольников с целыми сторонами и медианами связана с простыми числами. Сначала это кажется не совсем очевидным, но если следующее тождество является верным

то медиана не может быть целым числом. А это значит, что сама задача поиска треугольников с целыми сторонами и медианами наверняка может быть переведена на язык теории чисел, правда не знаю как.

В заключение

Сама идея того, что можно навести какой-никакой порядок в неупорядоченных множествах, очень любопытна. Например, можно попытаться каким-нибудь образом упорядочить матрицы из натуральных чисел, или графы определенного типа. Можно ли извлечь какую-то пользу от такого упорядочивания, это уже другой вопрос.