У геологов свой майнкрафт: как построить то, что не знаешь, по тому, что знаешь

Это начало истории о том, как сначала математика вторглась в геологию, как потом пришёл айтишник и всё запрограммировал, создав тем самым новую профессию «цифрового геолога». Это рассказ о том, чем стохастическое моделирование отличается от кригинга. А также это попытка показать, как ты сам можешь написать свой первый геологический софт и, возможно, как-то преобразить отрасль геологического и нефтяного инжиниринга.

Посчитаем, сколько там нефти

Чтобы посчитать, сколько нефти находится в месторождении, как она распределена в пространстве, и как будет идти процесс её добычи, умные люди строят разного рода модели месторождения. Исходной информацией для моделирования являются, в первую очередь, различного рода исследования стволов скважин. Также привлекают множество другой дополнительной информации, которая косвенным или прямым образом характеризует породу или насыщающие её жидкости (нефть, воду или газ). Ну а чтобы жизнь нефтяного инженера не была похожей на сказку, исходные данные имеют различную точность, различную физическую природу, распределены в пространстве неравномерно и характеризуют разный объём породы.

Существуют разные модели, позволяющие охарактеризовать месторождение. Например, если мы по скважинам узнаем среднюю толщину продуктивного пласта $$, по изъятому керну посчитаем среднюю пористость $$ и нефтенасыщенность $$, «прикинем» площадь месторождения $$, то формула $$ является простейшей (можно назвать нуль-мерной) моделью запаса нефти. (Если слова пористость и нефтенасыщенность вызывают у вас дискомфорт, приглашаем прочитать одну из предыдущих статей нашего блога)

Соорудить такую модель — полезное упражнение, однако в реальной практике, конечно, приходится строить более сложные и точные модели, позволяющие не только оценить запасы, но и в итоге построить гидродинамические модели процесса разработки, учитывающие неравномерное распределение свойств пласта в пространстве, неравномерное распределение давления и динамику вытеснения нефти.

Пусть месторождение описывается трехмерной областью $$, а $$ — это точка из множества $$. Тогда пусть $$ будет значением пористости в точке $$, а $$ — значением нефтенасыщенности. Тогда формула $$ — будет уже трехмерной моделью запаса нефти. Задачей инженера является построение трехмерных полей $$, $$ (а также проницаемости, насыщенности газа, воды и других величин) в объёме месторождения $$. А перед этим конечно нужно ещё оконтурить сам геометрический объект $$. И всё это можно назвать задачами интерполяции, подразумевая, что на основе точечных измерений тех или иных пространственных величин в скважинах нужно построить прогноз распределения их значений между скважинами (на самом деле не только между ними, но также и в неразбуренной области, в этом смысле это и задачи экстраполяции тоже).

В этой статье мы попробуем кратко и популярно поговорить о методах интерполяции в приложении к геологическому моделированию. С полным осознанием того, что каждая формула по Стивену Хокингу уменьшает количество читателей в два раза, а к данному моменту было приведено уже две формулы, нам всё же не удастся добраться до конца, не написав ещё несколько формул. Мы сделаем это в максимально понятной форме — не для того вы уже прочли столько слов, чтобы уйти со страницы, ничего не поняв. К тому же цель нашего блога — обозначить проблематику и показать актуальные задачи нефтянки для специалистов в других областях, чтобы зародить диалог и, мы надеемся, взаимовыгодное сотрудничество. Поэтому призываем, физически оставаясь на диване, мысленно с него приподняться и двинуться в дебри нефтяной инженерной науки.

Осложнять нам путь будет множество факторов. Попробуем некоторые из них перечислить; это, собственно, и будут те вызовы, с которыми имеют дело нефтяные инженеры и разработчики софта для нефтяного и геологического моделирования.

Косвенный характер исходных данных

Поскольку информация о породе на глубине в несколько километров стоит очень дорого, в ход идёт всё, что может прямо или косвенно охарактеризовать наш продуктивный пласт. Напомним, нефтяников интересуют, прежде всего, свойства пустотного пространства, а не сама порода. В первую очередь, это упомянутые пористость и проницаемость.

Однако непосредственно пористость и проницаемость мы можем лицезреть лишь в редких образцах породы, извлекаемых при бурении разведочных скважин с отбором керна (как он выглядит, мы показывали в этой статье). Объём таких исследований очень невелик и явно недостаточен, чтоб описать месторождение. К тому же на стол лаборатории попадают только цилиндры размером в несколько сантиметров, высверленные в выборочных местах из колонки керна, который не рассыпался при извлечении и лежит в ящиках достаточно большими и прочными кусками.

Поэтому сами данные керна в интерполяции и прогнозе межскважинного пространства не участвуют, а участвуют данные, полученные косвенным образом в виде корреляций через посредство геофизических исследований, которые уже проводят практически на всех скважинах. В скважину после бурения спускают гирлянду геофизических приборов, которые записывают сигналы различной физической природы, которые позже сопоставляются со значениями керна. Полученные закономерности используются уже во всем фонде скважин, чтобы рассчитать интересующие нас параметры породы. Этим занимается геофизическая наука. Если вам кажется, что в такой косвенности нет никакой проблемы, то представьте себе, что в травмпункте кто-то пытливый посчитал корреляцию между плотностью костной ткани и ростом пациентов с переломами, а потом применил эту зависимость ко всему населению.

Итак, косвенный характер исходных данных — первый осложняющий фактор, который надо иметь в виду и осознавать его последствия.

Носитель или объём осреднения

Второй особенностью является объём осреднения, который неявно стоит за любым значением, таким как пористость или проницаемость и т.д. Если сделать мысленный эксперимент и рассмотреть точку пласта, в ней может находиться либо камень, либо жидкость. Самой пористости в точке нет, а возникает она в результате объёмного осреднения, когда рассматривается определённого размера и формы окрестность точки, в ней рассчитывается объём пор и делится на объём этой области. Область называется математически носителем или — в англоязычной литературе — словом «support». Тоже самое, только с дополнительными сложностями, относится и к проницаемости, поскольку надо понимать, проницаемость в каком направлении имеется в виду. Безотносительно носителя говорить об объёмных величинах не имеет никакого смысла.

Южноафриканский учёный Денни Криге, обрабатывая статистические данные запасов полезных ископаемых, экспериментально установил зависимость вариации величин от объёма осреднения (Krige, D.G. 1951. A statistical approach to some basic mine valuation problems on the Witwatersrand. Journal of the Chemical, Metallurgical and Mining Society of South Africa, December 1951. pp. 119–139.). Что, в общем-то, очевидно, чем на большие куски мы мысленно распилим породу, тем меньше стоит ожидать изменчивость величин, которые усредняются по их объёму. Значит, пористость, измеренная в кусочках керна размером 5×5 см, и пористость, оценённая по геофизическим исследованиям скважин, охватывающим пласт породы глубиной до 1 м, и пористость в ячейках цифровой геологической модели размером 50 м×50 м×1 м — это всё разные пористости, и у них разные статистические закономерности, связанные друг с другом правилами перемасштабирования (ещё одно иностранное слово — upscaling).

Хватит воды

Давайте теперь уже напишем несколько формул. Пусть мы говорим об интерполяции некоторой пространственной величины $$, где $$ — это точка в пространстве или на плоскости. И пусть в некоторых точках нам известны значения $$. Тогда функция многих аргументов

будет интерполятором. Естественно требовать, чтобы выполнялись тождества

то есть интерполяция в точку с уже известным значением должна давать это самое значение.

Чаще всего строятся линейные интерполяторы вида

где $$ — некоторые веса, которые зависят от точек $$ и $$. И откроем программистам и айтишникам великую тайну, почему математики так любят линейные модели. А любят они их не потому, что они лучше описывают мир, а потому что это единственное, что зачастую они могут посчитать.

Давайте напишем самый простой интерполятор:

где $$ — некоторый показатель. Если $$ то это метод обратных расстояний (см. рис. 1). А если $$, то это метод обратных квадратов расстояний. Метод обратных расстояний будет давать острые пики в точках данных, метод обратных квадратов расстояний будет давать гладкие перегибы в точках данных. Очевидно в эту формулу нельзя просто так подставить в правую часть $$, потому что возникнет деление на ноль. Но зато, если постепенно приближать $$ к $$, вес при соответствующем $$ будет стремиться к 1, в то время как веса при всех остальных $$ будет стремиться к нулю, поэтому $$ принудительно приравнивается к $$.

Ниже приведена простейшая Python программа для интерполяции методом обратных расстояний.

import numpy as np
import matplotlib.pyplot as pl

# num of data
N = 5

np.random.seed(0)

# source data
z = np.random.rand(N)
u = np.random.rand(N)

x = np.linspace(0, 1, 100)
y = np.zeros_like(x)

# norm weights
w = np.zeros_like(x)

# power
m = 2

# interpolation
for i in range(N):
    y += z[i] * 1 / np.abs(u[i] - x) ** m
    w += 1 / np.abs(u[i] - x) ** m

# normalization
y /= w

# add source data
x = np.concatenate((x, u))
y = np.concatenate((y, z))
order = x.argsort()
x = x[order]
y = y[order]

# draw graph
pl.figure()

pl.scatter(u, z)
pl.plot(x, y)

pl.show()

pl.close()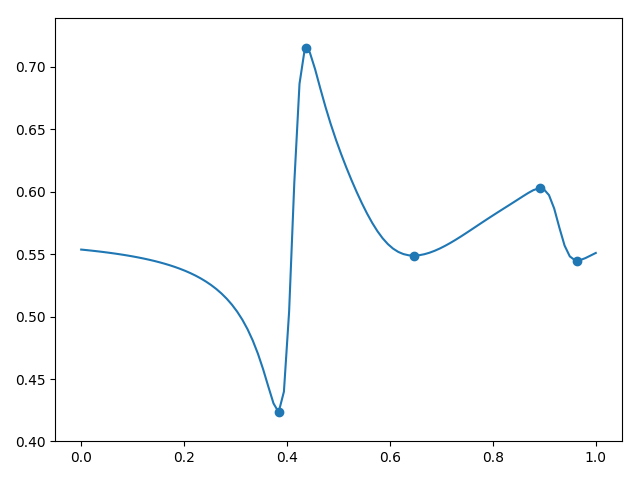

Рисунок 1. Интерполяция методом обратных расстояний

Самосогласованность

Проведём мысленный эксперимент. Предположим, мы воспользовались определённым алгоритмом интерполяции, чтобы предсказать глубину пласта в какой-либо точке на основе ранее пробуренных скважин в окрестности. Предположим затем, что мы пробурили в данном месте скважину, и прогноз был полностью оправдан. Какая радость и для геолога-инженера, и для разработчика софта, и для прикладного математика, что их прогноз оправдался, верно? Это убедит нас, что предположения приняты верно и используемая математическая модель неплоха и должна использоваться дальше. Давайте теперь включим пробуренную скважину в список исходных данных и применим ту же математическую модель, только теперь данных у нас больше на 1 штуку. Логично ожидать, что прогноз не должен никак измениться, ведь предыдущая скважина только подтвердила его. А вот на те, этот тест проваливают примитивные алгоритмы пространственной интерполяции, такие как описанный ранее метод обратных расстояний (см. рис. 2). Поэтому такие алгоритмы из арсенала интерполяционных методов сразу отправляются на свалку.

Рисунок 2. Несамосогласованность метода обратных расстояний

Декластеризация

Существует такой хрестоматийный кейс, когда горный инженер, обрабатывая статистические данные некоторого рудного месторождения, провел осреднение содержания полезной руды в образцах, умножил на объём месторождения и получил чрезвычайно привлекательные цифры. Только он не учёл, что преимущественные места отбора были сосредоточены как раз в самых лакомых участках месторождения, то есть данные его несколько тенденциозны. Такой ошибки не должны совершать и нефтяники, поскольку первые скважины очевидно бурятся в самых продуктивных местах. Декластеризация — имя этому действию, смысл которого в том, чтобы придать данным определённый вес в соответствии с их расположением: данные, находящиеся в непосредственной близости друг от друга, значат меньше, чем данные в отдельных точках. Насколько меньше и как это считать, вытекает из статистической модели пространственных величин.

Ещё немного математики

Взглянем на формулу (2) немного под другим ракурсом:

то есть результат можно понимать, как линейную комбинацию некоторых функций координат, каждая из которых равняется единице в соответствующей точке данных и нулю во всех остальных. Так как функции построены таким специальным образом, нам не пришлось решать никаких систем линейных уравнений, поскольку $$-ая функция никак не влияет на $$-ую точку. Но эта простота и делает алгоритм несамосогласованным.
Построим другой, более сложный интерполятор:

где функция от расстояния $$ как правило монотонно-убывающая и стремящаяся к нулю на бесконечности, а $$ — весовые коэффициенты. То есть модель (2) — это линейная комбинация одинаковых функций «шапочек», центры которых расположены в точках данных. Осталось правильно рассчитать веса $$. Что бы сделать это, надо добиться выполнения тождеств (1):

что порождает систему линейных уравнений на $$. В матричном виде мы можем записать её в виде $$, где $$ — столбец значений $$, $$ — столбец искомых весов, $$ — матрица взаимных значений функции «шапочки» $$ между точками данных. Математик тут сразу запишет, что $$, и подставит это в (6), в итоге получит что

где

Формула (6) является одним из вариантов интерполяции методом кригинга (имени того самого Дени Криге). А формула (4) является другим вариантом записи того же кригинга, только в слегка развёрнутом виде, именуемым в англоязычной литературе как dual kriging. Сравните формулы (6) и (3), вроде тоже самое, только функции $$ построены иначе. Если подставить вместо $$ точку $$, то в формуле (7) опытный глаз заметит, что матрица, обратная к матрице $$, умножается на один из её столбцов, из чего следует что $$ и $$ для любых $$ (так же как у функций $$).

В любой литературе по численному моделированию геологии вы неизбежно увидите подобные формулы и встретитесь с интерполяцией методом кригинга (см. рис. 3). А всё потому, что эта интерполяция самосогласована и выполняет декластеризацию, о которой мы говорили выше.

Предлагаю убедиться, что кригинг — это всего несколько программных строк на языке Python:

import numpy as np
import matplotlib.pyplot as pl

# num of data
N = 5

np.random.seed(0)

# source data
z = np.random.rand(N) - 0.5
u = np.random.rand(N)

x = np.linspace(0, 1, 100)
y = np.zeros_like(x)

# covariance function
def c(h):
    return np.exp(-np.abs(h ** 2 * 20.))

# covariance matrix
C = np.zeros((N, N))

for i in range(N):
    C[i, :] = c(u - u[i])

# dual kriging weights
lamda = np.linalg.solve(C, z)

# interpolation
for i in range(N):
    y += lamda[i] * c(u[i] - x)

# add source data
x = np.concatenate((x, u))
y = np.concatenate((y, z))
order = x.argsort()
x = x[order]
y = y[order]

# draw graph
pl.figure()

pl.scatter(u, z)
pl.plot(x, y)

pl.show()

pl.close()

Рисунок 3. Интерполяция методом кригинга

Сглаживающий эффект

Ничего принципиально более совершенного, чем интерполяция методом кригинга для геологии, до сих пор не придумано. Именно формулы (5) и (6) применяются в дорогущих пакетах геологического моделирования, когда строятся пространственные поля пористости и проницаемости для оценки запасов месторождения.

Представим теперь, что мы хотим построить пространственное распределение характеристик породы, чтобы в последующем моделировать фильтрацию флюидов и процесс нефтеизвлечения. Оказывается, для гидродинамики важны не только абсолютные значения пористости и проницаемости, но и их изменчивость, прерывистость в пространстве.

Представим себе две скважины с хорошими свойствами породы на расстоянии двух километров друг от друга. Предположим, что мы знаем (догадываемся), что в среднем хорошие свойства породы сохраняются на протяжении, например, одного километра, и затем сменяются плохими. Значит, между скважинами с определённой вероятностью может возникнуть соответствующий «провал», который способен сильно повлиять на протекание жидкости от одной скважины к другой. Однако, глядя на базовую формулу (6), можно заметить, что это линейная комбинация функций «шапочек», помещённых в точки данных. Значит, из интерполяции методом кригинга этот «провал» никак не возникает. Представим другой пример: на месторождении расположено множество скважин в центральной части и редкие разведочные скважины на крыльях. Поскольку это интерполяция, изменчивость результата в центральной части будет максимальна, изменчивость на крыльях будет снижаться, а дальше — и вовсе затухать. Очевидно, что изменчивость пласта вряд ли зависит от того, где и как плотно мы расположили скважины.

Интерполяция на основе имеющихся данных даёт нам наиболее ожидаемое значение в каждой точке пласта. Для подсчёта запасов нефти это как раз то, что нужно. Однако для построения гидродинамической модели это нам принципиально не подходит. О том, что придумано взамен, пойдёт речь дальше.

Детерминистика и стохастика

Поднимем немного температуру на нашем математическом градуснике и импортируем модуль теории вероятности и линейной алгебры.

from theory import probability
from numpy import linalg

У кого данные библиотеки не установлены, наверное, придётся ограничиться неполным пониманием текста.

Чтобы преодолеть сглаживающий эффект метода кригинга, было придумано стохастическое моделирование. Стохастический подход рассматривает распределение наших пространственных величин в пласте как стохастическое (случайное) поле: в каждой точке пласта u мы рассматриваем $$ как случайную величину, но все эти случайные величины связаны друг с другом (не независимы друг от друга). И задача стоит синтезировать один или несколько вероятных представителей случайного поля при том, что нам известны некоторые значения $$.

Заметим здесь важное логическое отличие. Интерполяция даёт нам оценку или наиболее ожидаемое значение в каждой точке пласта. Стохастическая же модель претендует на синтез таких распределений свойств пласта в межскважинном пространстве, которые могли бы быть похожими на реальность (с точки зрения принятых предположений и гипотез, конечно).

Само по себе утверждение, что что-то под землёй является случайным — не более чем математическая абстракция. Но чтобы что-то начать считать, нужно эту модель ещё конкретизировать. Математик однажды сказал следующее: пусть в каждой точке пространства $$ — гауссова случайная величина (имеющая нормальное распределение вероятности), а в совокупности любой набор случайных гауссовых величин $$, взятых в произвольном наборе точек $$, является мультигауссовым, то есть подчиняется специальной многомерной функции распределения. То есть $$ — это мультигауссово случайное поле, реализацию которого мы хотим синтезировать.

Для любых двух мультигауссовых случайных величин их ковариация (ковариация по определению $$, её можно образно сравнить с углом между двумя векторами в пространстве) исчерпывающим образом описывает их взаимозависимость. А взаимозависимость набора случайных величин задаётся ковариационной матрицей — ковариацией каждой случайной величины с каждой. А для случайного поля, в котором в любой точке u соответствует своя случайная величина $$, нужно построить ковариационную функцию.

Математик дополнительно предположил, что случайное поле геологического параметра является стационарным, то есть ковариационная функция является функцией только расстояния между точками: $$. Да-да, ковариационная функция $$ — это та самая функция «шапочка» в интерполяции кригинга в формуле (4), но здесь более полно раскрывается её смысл: $$ количественно описывает возможность прогнозировать значение параметра на расстоянии $$ по его значению в точке. Например, если $$, то на расстоянии $$ метров наша уверенность в прогнозе составляет $$ у.е., а если $$, то знание о значении в данной точке абсолютно бесполезно для прогноза того, что будет через километр.

Стационарная гауссова случайная модель приобрела большую популярность не потому, что она лучше описывает мир, а потому, что это практически единственное, что мы можем посчитать. Дело в том, что гауссовы случайные величины можно умножать на числа и складывать друг с другом, при этом будут получаться другие гауссовы случайные величины. И ещё про них доказано, что если ковариация гауссовых случайных величин равна нулю, то они независимы. Сказанное позволяет любой мультигауссовый набор случайных величин $$ выразить в виде линейной комбинации независимых гауссовых случайных величин $$ с нулевым математическим ожиданием и единичной дисперсией. В матричном виде запишется

Чтобы найти матрицу $$, нужно выразить получившуюся ковариационную матрицу (попарную ковариацию каждого элемента $$ с каждым). В матричном виде:

здесь мы воспользовались тем, что случайные величины $$ независимы, и, значит, ковариационная матрица $$ является единичной. Последняя формула даёт нам ключ к стохастическому моделированию. Для набора случайных величин $$, которые мы хотим синтезировать, нужно составить ковариационную матрицу $$, найти любое её разложение вида $$ (таких много) и тем самым выразить набор взаимосвязанных случайных величин $$ через набор независимых случайных величин $$, а это то, что математику и нужно. Последние легко можно синтезировать с помощью генератора псевдослучайных величин. Это называется стохастическим гауссовым моделированием.

Примечательно, что стохастическое моделирование в самом своём принципе подразумевает возможность моделировать вообще без исходных данных (а если быть точным, то без самих скважинных данных, но с предположениями о неоднородности моделируемого геофизического параметра пласта — среднее, дисперсия и вариограмма). Ниже приведём простейшую программу стохастического гауссова моделирования, не учитывающую исходные данные (см. рис. 4).

import numpy as np
import matplotlib.pyplot as pl

np.random.seed(0)

# source data
N = 100
x = np.linspace(0, 1, 100)

# covariance function
def c(h):
    return np.exp(-np.abs(h ** 2 * 250))

# covariance matrix
C = np.zeros((N, N))

for i in range(N):
    C[i, :] = c(x - x[i])

# eigen decomposition
w, v = np.linalg.eig(C)

A = v @ np.diag(w ** 0.5)

# you can check, that C == A @ A.T

# independent normal values
zeta = np.random.randn(N)

# dependent multinormal values
Z = A @ zeta

# draw graph
pl.figure()

pl.plot(x, Z)

pl.show()

pl.close()

Рисунок 4. Несколько реализаций стохастического гауссового процесса без учёта данных

Для учёта исходных данных в стохастическом моделировании нужно строить постериорную ковариацию или, иными словами, нужно построить условную функцию распределения (при условии, что нам известны значения в некоторых точках). Это уже немного сложно объяснить в двух словах, но для любопытных мы приведём пример исходного кода и результат на рисунке 5.

import numpy as np
import matplotlib.pyplot as pl

np.random.seed(3)

# source data
M = 5

# coordinates of source data
u = np.random.rand(M)

# source data
z = np.random.randn(M)

# Modeling mesh
N = 100
x = np.linspace(0, 1, N)

# covariance function
def c(h):
return np.exp(−np.abs(h ∗∗ 2 ∗ 250))

# covariance matrix mesh−mesh
Cyy = np.zeros ((N, N))
for i in range (N):
    Cyy[ i , : ] = c(x − x[i])

# covariance matrix mesh−data
Cyz = np.zeros ((N, M))

# covariance matrix data−data
Czz = np.zeros ((M, M))
for j in range (M):
    Cyz [:, j] = c(x − u[j])
    Czz [:, j] = c(u − u[j])

# posterior covariance
Cpost = Cyy − Cyz @ np.linalg.inv(Czz) @ Cyz.T

# lets find the posterior mean, i.e. Kriging interpolation
lamda = np.linalg.solve (Czz, z)
y = np.zeros_like(x)

# interpolation
for i in range (M):
    y += lamda[i] ∗ c(u[i] − x)

# eigen decomposition
w, v = np.linalg.eig(Cpost)
A = v @ np.diag (w ∗∗ 0.5)

# you can check, that Cpost == A@A.T

# draw graph
pl.figure()
for k in range (5):
    # independent normal values
    zeta = np.random.randn(N)
    # dependent multinormal values
    Z = A @ zeta
    pl.plot(x, Z + y, color=[(5 − k) / 5] ∗ 3)
    pl.plot(x, Z + y, color=[(5 − k) / 5] ∗ 3, label=’Stochastic realizations’)

pl.plot(x, y, ’. ’, color=’blue’, alpha=0.4, label=’Expectation(Kriging)’)
pl.scatter(u, z, color=’red ’, label=’Source data’)
pl.legend()
pl.show()
pl.close()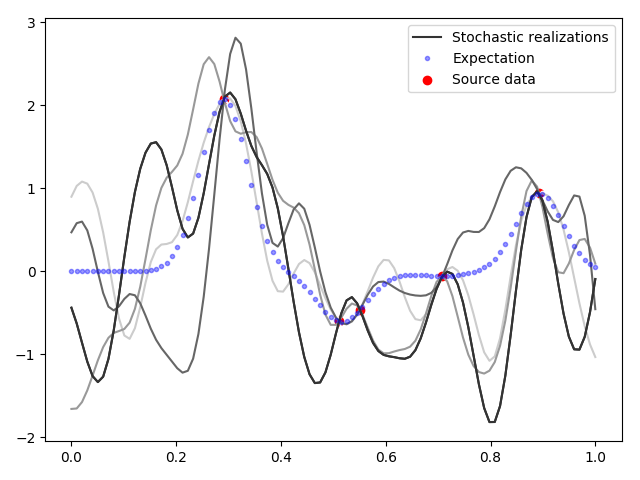

Рисунок 5. Несколько реализаций стохастического гауссова процесса с учётом данных

Как видим на графиках рисунка 5, стохастические реализации собираются вместе в точках данных и вновь расходятся по своим случайным траекториям. Изменчивость стохастических реализаций уже не зависит от плотности расположения исходных данных, и, глядя на них, уже невозможно угадать, где скважин было больше (в отличие от интерполяции). Однако таких стохастических распределений получается бесчисленное множество, и все они равновероятны с точки зрения геологии, и все они будут удовлетворять исходным данным. Какую случайную геологическую модель выбрать гидродинамику и что с ней делать — до сих пор не решённый до конца практический вопрос.

Если сделать $$ стохастических реализаций геологической модели, посчитать среднее значение между ними в каждой точке, то окажется, что мы получим очень близкую картину к результату интерполяции методом кригинга (6). Таким образом, данный метод даёт нам математическое ожидание или самое вероятное значение в каждой отдельно взятой точке пласта, а стохастическое моделирование даёт нам равновероятные случайные картины распределения геологического параметра во всём объёме пласта сразу (каждая из которых, между прочим, совсем не похожа на интерполяцию методом кригинга).

Попытаемся привести ещё одно рассуждение, поясняющее разницу между интерполяцией и моделированием. Предположим, мы пытаемся сделать прогноз температуры на июль. Очевидно в средней полосе России должно быть тепло и в целом солнечно. Однако каждый знает, что погода у нас редко бывает долго стабильная, и теплые дни неизменно сменяются прохладными, а солнце — дождями и грозами. Например, в среднем после пяти солнечных дней должно быть два пасмурных. Синтез такого правдоподобного погодного графика — это моделирование. А утверждение, что в среднем будет что-то около 22 градусов — интерполяция. Аналогичная интерполяция на март даст вам -5 С, а моделирование — постоянные прыжки туда-сюда через ноль. Очевидно, что тот, кто будет пытаться на основании этого делать предсказания на вредное влияние климата на асфальт, сделает диаметрально противоположные выводы!

А как происходит моделирование в пространстве?

Приведённые выше примеры являются одномерными и тривиальными. В случае геологического моделирования пространственные объекты (2D и 3D), где все теоретические выкладки имеют тот же математический смысл (что и для 1D случая), а, с точки зрения программирования, разница только в размерности numpy массивов и в объёмах вычислений.

Для демонстрации простого, но максимально близкого к геологическому моделированию примера, на рисунке 6 представлена простая «пятискважинная» псевдо-модель.

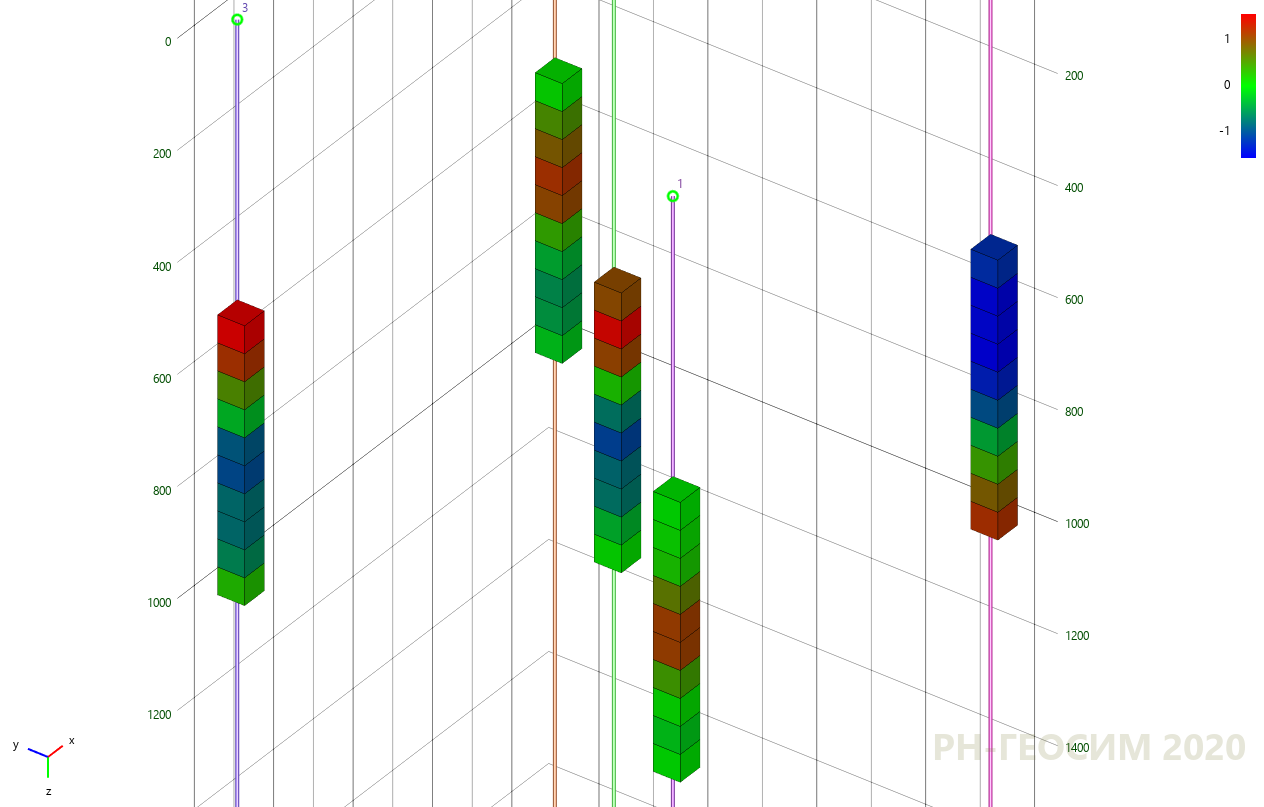
Рисунок 6. «Пятискважинная» псевдо-модель

В определенных ячейках рассматриваемого объёма расположены «скважинные данные». Цветом показано распределение некоторого числового параметра, например пористости или проницаемости. Требуется провести моделирование неизвестных ячеек («межскважинного пространства») методами кригинга (рис. 7) и стохастического гауссова моделирования (рис. 8).

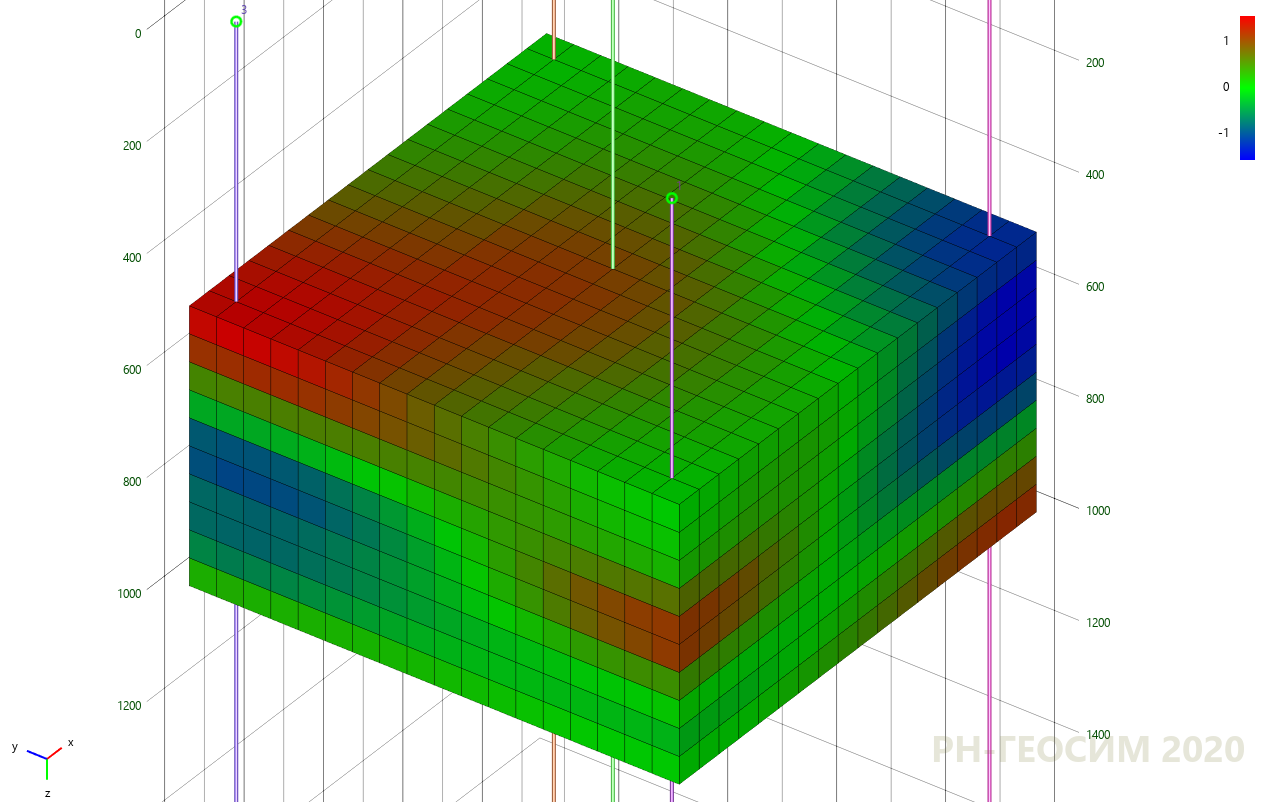
Рисунок 7. Применение метода кригинга на «пятискважинной» псевдо-модели

Рисунок 8. Применение метода стохастического гауссова моделирования на «пятискважинной» псевдо-модели

Как видно по рисункам 7 и 8 оба метода дают «похожую» картину моделирования, однако моделирование кригингом даёт чёткий детерминированный образ, который будет воспроизводиться каждый раз при последующем моделировании, а стохастическая реализация более «реалистична» и каждый раз уникальна.

Пример из «реальной» практики

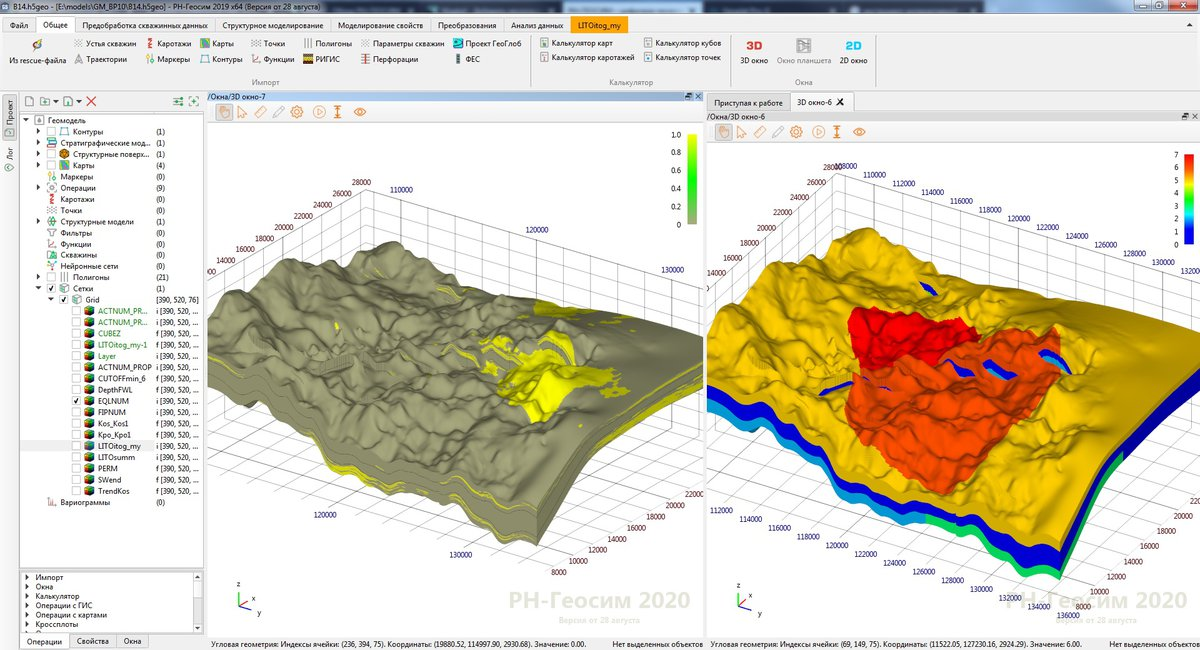
Но самое интересное происходит именно на данных, приближенных к реальным объектам. Например, модель «X» абстрактного месторождения «Y», на которой цветом показано уже распределение некоторого геологического параметра в объёме конкретного пласта. Моделирование методом кригинга представлено на рисунке 9.

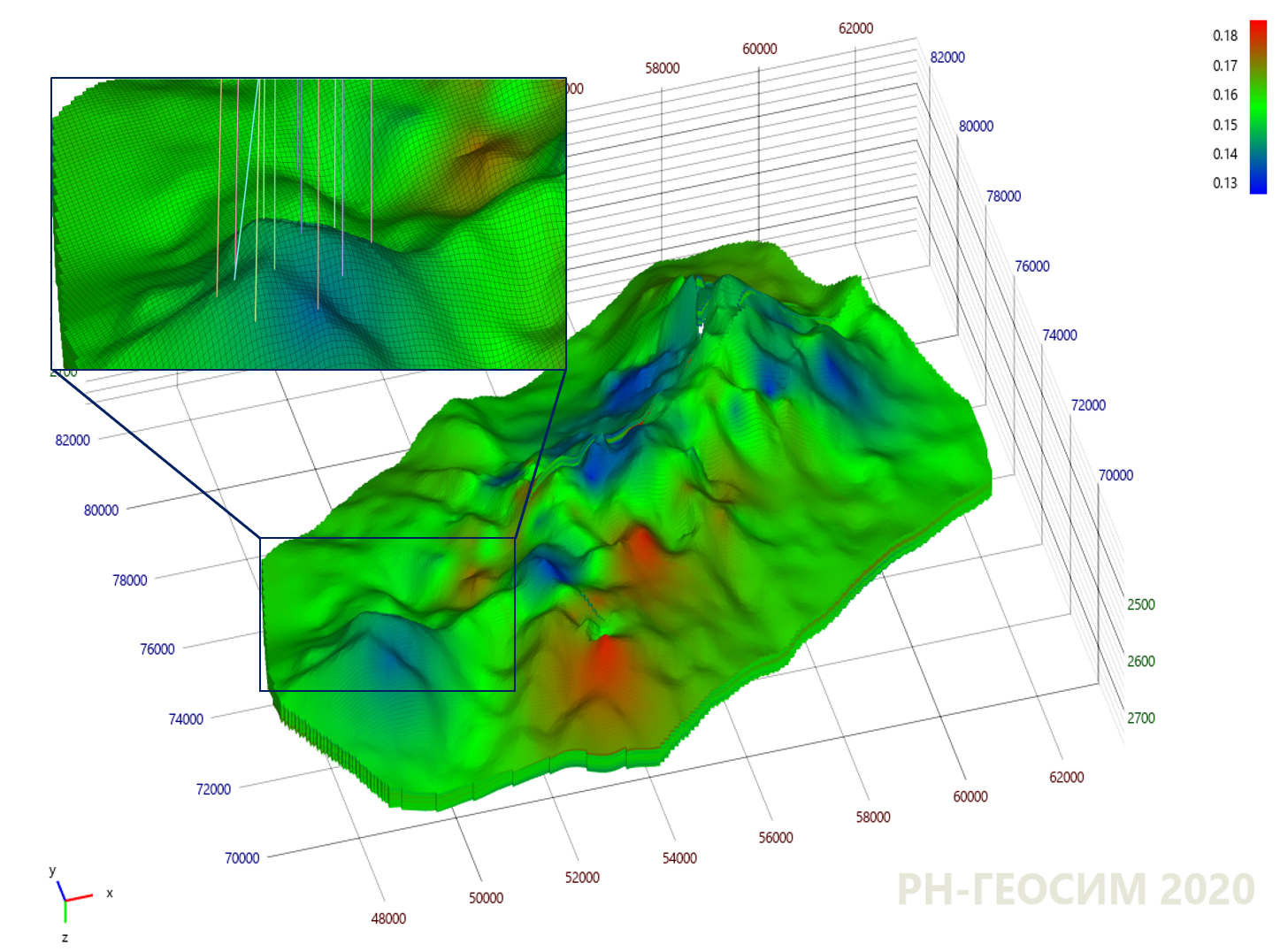
Рисунок 9. Применение метода кригинга на модели "X"

Области с синими и красными цветами связаны со скважинами, имеющими минимальные и максимальные значения параметра. Кригинг соединил скважины друг с другом плавными переходами без резких скачков, а пространство в областях, далёких от скважин — устремил к среднему значению (зелёный цвет). Но картина со стохастическим моделированием имеет немного другой характер (см. рис. 10).

Рисунок 10. Применение метода стохастического гауссова моделирования на модели "X"

На рисунке 10 уже видны пятна, которые были синтезированы случайным алгоритмом в соответствии с принятыми гипотезами о пространственной изменчивости геологического параметра, однако области с повышенными и пониженными значениями по-прежнему идентифицируются.

Выводы

Целью нашей статьи было показать, что в части пространственной интерполяции в геологии нет ничего принципиально сложного. Прототипы этих геологических операций часто умещаются на одном экране. И между тем, это действительно математическое сердце дорогих и сложных программных продуктов. Современное геологическое моделирование не ушло далеко от простейших линейных моделей, и здесь ещё много можно сделать.

Разумеется, это не все интерполяционные модели, используемые в нефтяной геологии, мы не обсудили вопросы моделирования дискретных (категориальных) полей, негауссовых случайных полей и т. д. За кадром так же остались вопросы построения структурных моделей (геометрического моделирования нефтяных пластов), гидродинамическое моделирование и многое другое. Так что соответствующие статьи ещё появятся в нашем блоге. Хотелось бы получить от читателя отзыв, не был ли математический материал слишком сложным или непонятным? Совсем отказаться от математики не кажется правильным, потому что, по крайней мере, в нефтяном инжиниринге вырваться в конкуренции с существующими компаниями вперёд можно только за счёт синтеза следующих направлений:

• более совершенных и точно описывающих мир математических моделей;
• оптимального развёртывания математической модели в алгоритм;
• оптимальных численных реализаций, использующих особенности современных вычислительных систем.

Поэтому последующие статьи на тему, как что-то узнать, не вставая с дивана, будут содержать экскурсы в решения математических и физических задач, и, возможно, вызовут у читателей дополнительный интерес к фундаментальным областям науки, без которых решение многочисленных задач разведки и добычи не представляется возможным.