Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!

Фото взято из публикации
Введение
Одна из наиболее актуальных задач цифровой обработки сигналов – задача очистки сигнала от шума. Любой практический сигнал содержит не только полезную информацию, но и следы некоторых посторонних воздействий помехи или шума. Кроме этого, при вибродиагностике сигналы от вибродатчиков имеют не стационарный частотный спектр, что усложняет задачу фильтрации.
Существует множество различных способов удаления высокочастотного шума из сигнала. Например, библиотека Scipy содержит фильтры, основанные на различных методах фильтрации: Калмана; сглаживание сигнала путём его усреднения по оси времени, и другие.
Однако, преимущество метода дискретного вейвлет преобразования (DWT) состоит в многообразии форм вейвлет. Можно выбрать вейвлет, который будет иметь форму, характерную для ожидаемых явлений. Например, можно выделить сигнал в заданном частотном диапазоне, форма которого отвечает за появление дефекта.
Целью настоящей публикации является анализ методов фильтрации сигналов вибродатчиков с применением DWT преобразования сигнала, фильтра Калмана и метода скользящего среднего.
Исходные данные для анализа
В публикации работу фильтров основанных на различных методах фильтрации будем анализировать используя набор данных НАСА. Данные получены на экспериментальной платформе PRONOSTIA:

Набор содержит данные о сигналах вибродатчиков по износу подшипников различных типов. Назначение папок с файлами сигналов приведено в таблице:
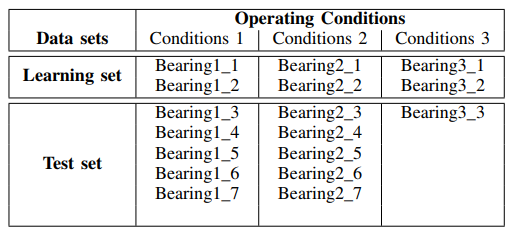
Мониторинг состояния подшипников обеспечивается сигналами датчиков вибрации (горизонтальным и вертикальным акселерометрами), силы и температуры.

Сигналы получены для трёх различных нагрузок:
- Первые рабочие условия: 1800 об / мин и 4000 Н;
- Вторые рабочие условия: 1650 об / мин и 4200 Н;
- Третьи рабочие условия: 1500 об / мин и 5000 Н.
Для этих условий, используя непрерывное вейвлет преобразование сигналов, построим скалограммы мощности спектра для данных из тестового набора — по одному файлу (для одного типа подшипников) из папок: ['Test_set/Bearing1_3/acc_00001.csv','Test_set/Bearing2_3/acc_00001.csv', 'Test_set/Bearing3_3/acc_00001.csv'] (см.табл.1).
Листинг скалеограмм
import scaleogram as scg
import pandas as pd
from pylab import *
import pywt
filename_n = ['Test_set/Bearing1_3/acc_00001.csv', 'Test_set/Bearing2_3/acc_00001.csv',
'Test_set/Bearing3_3/acc_00001.csv']
for filename in filename_n:
df = pd.read_csv(filename, header=None)
signal = df[4].values
wavelet = 'cmor1-0.5'
ax = scg.cws(signal, scales=arange(1, 40), wavelet=wavelet, figsize=(8, 4), cmap="jet", cbar=None, ylabel='Период ', xlabel="Время ", yscale="log",
title='Вейвлет-преобразование сигнала %s \n(спектр мощности)'%filename)
show()

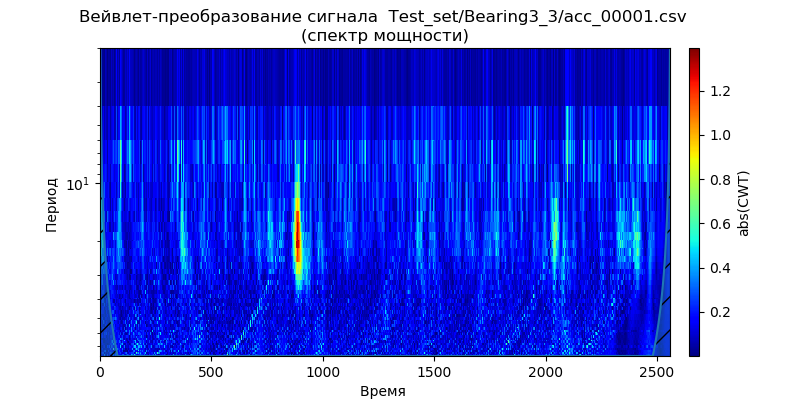
Из приведенных скалеограмм следует, что моменты увеличения мощности спектра возникают раньше по времени и демонстрируют периодичность для рабочих условий: 1650 об / мин и 4200 Н, что свидетельствует об ускоренной деградации подшипников в этой полосе частот для приведенного усилия. Этот сигнал ('Test_set/Bearing2_3/acc_00001.csv') мы и будем использовать для анализа методов удаления шума.
Деконструкция сигнала с помощью DWT
В публикации мы видели, как на DWT реализован банк фильтров, который может деконструировать сигнал в его частотные поддиапазоны. Коэффициенты аппроксимации (cA)представляют низкочастотную часть сигнала (фильтра усреднения). Коэффициенты детализации (cD) представляют высокочастотную часть сигнала. Далее мы рассмотрим, как можно использовать DWT для деконструкции сигнала в его частотные поддиапазоны и восстановления исходного сигнала.
Решить задачу деконструкции сигнала используя средства PyWavelets можно двумя способами:
Первый способ — применить к сигналу pywt.dwt() для извлечения коэффициентов аппроксимации и детализации (cA1, cD1). Затем для восстановления сигнала будем использовать pywt.idwt():
Листинг
import pywt
from scipy import *
import pandas as pd
from pylab import *
filename = 'Test_set/Bearing2_3/acc_00001.csv'
df = pd.read_csv(filename, header=None)
signal = df[4].values
(cA1, cD1) = pywt .dwt (signal, 'db2', 'smooth')
r_signal = pywt.idwt (cA1, cD1, 'db2', 'smooth')
fig, ax =subplots(figsize=(8,4))
ax.plot(signal, 'b',label='Оригинальный сигнал')
ax.plot(r_signal, 'r', label=' Восстановленный сигнал', linestyle='--')
ax.legend(loc='upper left')
ax.set_ylabel('Амплитуда сигнала', fontsize=12)
ax.set_xlabel('Время', fontsize=12)
ax.set_title(' Деконструкция сигнала (функция pywt.dwt()) \n Восстановление сигнала (функции pywt.idwt()) ')
show()
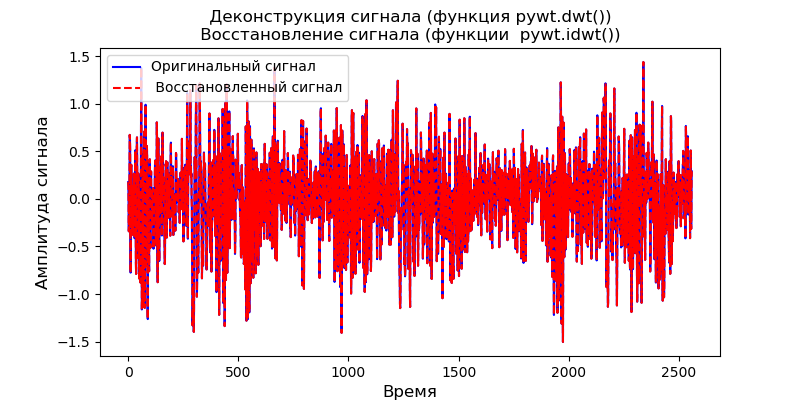
Второй способ применить к сигналу функцию pywt.wavedec(), чтобы восстановить все коэффициенты аппроксимации и детализации до некоторого уровня. Эта функция принимает в качестве входных данных исходный сигнал и уровень и возвращает один набор коэффициентов аппроксимации (n-го уровня) и n наборов коэффициентов детализации (от 1 до n-го уровня). Для деконструкции применим pywt.waverec ():
Листинг
import pywt
import pandas as pd
from pylab import *
filename = 'Test_set/Bearing3_3/acc_00026.csv'
df = pd.read_csv(filename, header=None)
signal = df[4].values
coeffs = pywt.wavedec(signal, 'db2', level=8)
coeffs = pywt.wavedec(signal, 'db2', level=8)
r_signal = pywt.waverec(coeffs, 'db2')
fig, ax = plt.subplots(figsize=(8,4))
ax.plot(signal, 'b',label='Оригинальный сигнал')
ax.plot(r_signal, 'r ',label= 'Восстановленный сигнал', linestyle='--')
ax.legend(loc='upper left')
ax.set_ylabel('Амплитуда сигнала', fontsize=12)
ax.set_xlabel('Время', fontsize=12)
ax.set_title(' Деконструкция до заданного уровня- level.\n Восстановление сигнала (функция pywt.wavedec()) ')
show()

Второй способ деконструкции и восстановления сигнала удобнее, он позволяет сразу установить требуемый уровень деконструкции.
Удаление высокочастотных шумов путём исключения части коэффициентов детализации в процессе деконструкции сигнала
Восстановим сигнал, удалив часть коэффициентов детализации. Поскольку коэффициенты детализации представляют высокочастотную часть сигнала, мы просто отфильтруем эту часть частотного спектра. При наличии высокочастотного шума в сигнале, это один из способов отфильтровать его.
В библиотеке PyWavelets это можно сделать при помощи функции пороговой обработки pywt.threshol():
pywt.threshold(data, value, mode= 'soft', substitute=0 )¶
data : array_like
Числовые данные.
value: scalar
Пороговое значение.
mode: {‘soft’, ‘hard’, ‘garrote’, ‘greater’, ‘less’}
Определяет тип порога, который будет применен к входным данным. По умолчанию ‘soft’.
substitute : float, optional
Подставляемое значение (по умолчанию: 0).
output : array
Пороговый массив.
Применение функции пороговой обработки для данного порогового значения лучше всего рассмотреть на следующем примере:
>>>> from scipy import*
>>> import pywt
>>> data =linspace(1, 4, 7)
>>> data
array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ])
>>> pywt.threshold(data, 2, 'soft')
array([0. , 0. , 0. , 0.5, 1. , 1.5, 2. ])
>>> pywt.threshold(data, 2, 'hard')
array([0. , 0. , 2. , 2.5, 3. , 3.5, 4. ])
>>> pywt.threshold(data, 2, 'garrote')
array([0. , 0. , 0., 0.9,1.66666667, 2.35714286, 3.])
График пороговых функций построим с помощью следующего листинга:
Листинг
from scipy import*
from pylab import*
import pywt
s = linspace(-4, 4, 1000)
s_soft = pywt.threshold(s, value=0.5, mode='soft')
s_hard = pywt.threshold(s, value=0.5, mode='hard')
s_garrote = pywt.threshold(s, value=0.5, mode='garrote')
figsize=(10, 4)
plot(s, s_soft)
plot(s, s_hard)
plot(s, s_garrote)
legend(['soft (0.5)', 'hard (0.5)', 'non-neg. garrote (0.5)'])
xlabel(' входное значение ')
ylabel('пороговое значение ')
show()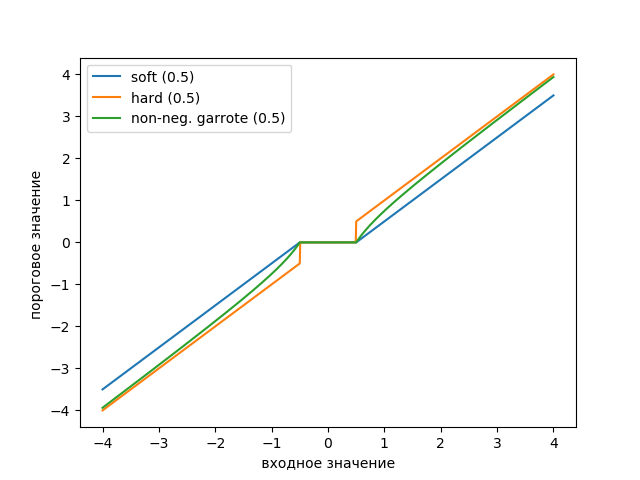
На графике показано, что неотрицательный порог Гаротта является промежуточным между мягким и твердым порогом. Требуется пара пороговых значений, которые определяют ширину переходной области.
Влияние пороговой функции на характеристики фильтра
Как следует из приведенного графика, нам подходят только две пороговые функции ‘soft’ и ‘garrote’, для исследования их влияния на характеристики фильтра, запишем листинг:
Листинг
import pandas as pd
from pylab import *
import pywt
filename = 'Test_set/Bearing2_3/acc_00001.csv'
df = pd.read_csv(filename, header=None)
signal = df[4].values
v='bior4.4'
thres=['soft' ,'garrote']
for w in thres:
def lowpassfilter(signal, thresh, wavelet=v):
thresh = thresh*nanmax(signal)
coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" )
coeff[1:] = (pywt.threshold(i, value=thresh, mode=w ) for i in coeff[1:])
reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" )
return reconstructed_signal
fig, ax = subplots(figsize=(8,4))
ax.plot(signal, color="b", alpha=0.5, label='Оригинальный сигнал')
rec = lowpassfilter(signal, 0.4)
ax.plot(rec, 'r', label='DWT преобразование сигнала', linewidth=2)
ax.legend()
ax.set_title('Удаление высокочастотного шума с помощью вейвлета :%s\n для пороговой функции:%s'%(v,w), fontsize=12)
ax.set_ylabel('Амплитуда сигнала', fontsize=12)
ax.set_xlabel('Время', fontsize=12)
show()
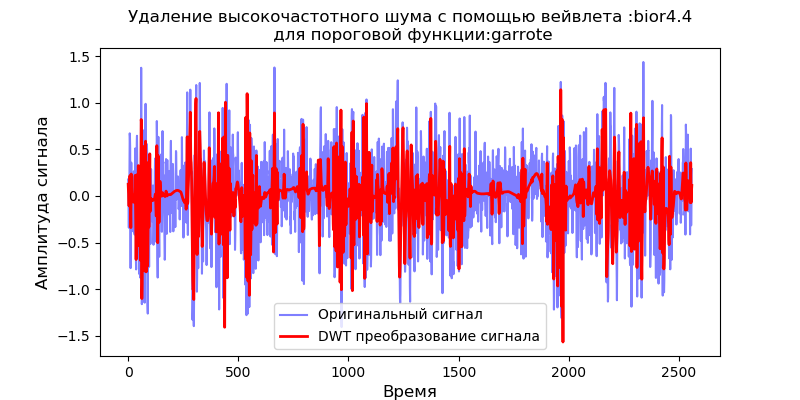
Как следует из приведенных графиков, функция soft обеспечивает лучшее сглаживание, чем функция ‘garrote’, поэтому функцию soft и будем использовать в дальнейшем.
Влияние порога детализации на характеристики фильтра
Для рассматриваемого типа фильтров порог смены коэффициентов детализации является важной характеристикой, поэтому исследуем её влияние с помощью следующего листинга:
Листинг
import pandas as pd
from pylab import *
import pywt
filename = 'Test_set/Bearing2_3/acc_00001.csv'
df = pd.read_csv(filename, header=None)
signal = df[4].values
v='bior4.4'
thres=[0.1,0.4,0.6]
for w in thres:
def lowpassfilter(signal, thresh, wavelet=v):
thresh = thresh*nanmax(signal)
coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" )
coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:])
reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" )
return reconstructed_signal
fig, ax = subplots(figsize=(8,4))
ax.plot(signal, color="b", alpha=0.5, label='Оригинальный сигнал')
rec = lowpassfilter(signal,w)
ax.plot(rec, 'r', label='DWT преобразование сигнала', linewidth=2)
ax.legend()
ax.set_title('Удаление высокочастотного шума с помощью вейвлета :%s\n для порога детализации %s'%(v,w), fontsize=12)
ax.set_ylabel('Амплитуда сигнала', fontsize=12)
ax.set_xlabel('Время', fontsize=12)
show()



Как следует из полученных графиков, уровень порога детализации влияет на масштаб отсеиваемых деталей. При увеличении порога вейвлет вычитает шум все большего уровня, пока не наступит излишнее укрупнение масштаба деталей и преобразование начнет искажать форму исходного сигнала.Для нашего сигнала порог должен быть не выше 0.63.
Влияние вейвлета на характеристики фильтра
В библиотеке PyWavelets имеется достаточное количество вейвлет для DWT преобразования, которые можно получить так:
>>> import pywt
>>> print(pywt.wavelist(kind= 'discrete'))
['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20']Влияние вейвлета на характеристику фильтра зависит от его первообразной функции. Для демонстрации этой зависимости выберем два вейвлета из семейства «Добеши» — db1 и db38, рассмотрим эти семейства:
Листинг
import pywt
from pylab import*
db_wavelets = ['db1', 'db38']
fig, axarr = subplots(ncols=2, nrows=5, figsize=(14,8))
fig.suptitle('Семейство вейвлетов Добеши: db1,db38', fontsize=14)
for col_no, waveletname in enumerate(db_wavelets):
wavelet = pywt.Wavelet(waveletname)
no_moments = wavelet.vanishing_moments_psi
family_name = wavelet.family_name
for row_no, level in enumerate(range(1,6)):
wavelet_function, scaling_function, x_values = wavelet.wavefun(level = level)
axarr[row_no, col_no].set_title("{} Уровень: {}. Исчезающие моменты : {}. Отсчёты:: {} ".format(
waveletname, level, no_moments, len(x_values)), loc='left')
axarr[row_no, col_no].plot(x_values, wavelet_function, 'b--')
axarr[row_no, col_no].set_yticks([])
axarr[row_no, col_no].set_yticklabels([])
tight_layout()
subplots_adjust(top=0.9)
show()
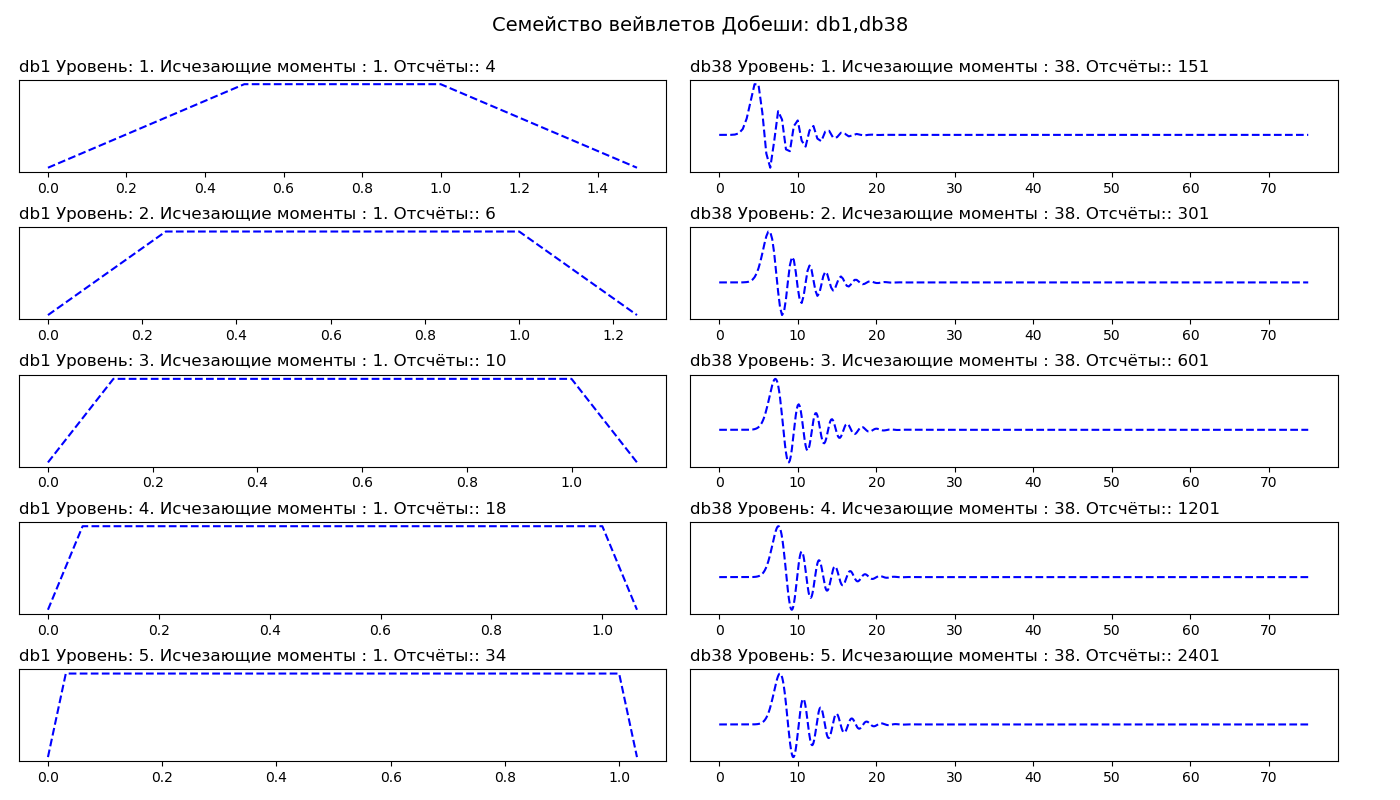
В первом столбце мы видим вейвлеты Добеши первого порядка (db1), во втором столбце тридцать восьмого порядка (db38). Таким образом, db1 имеет один момент исчезновения, а db38 имеет 38 моментов исчезновения. Число моментов исчезновения связано с порядком аппроксимации и гладкостью вейвлета. Если вейвлет имеет P моментов исчезновения, он может аппроксимировать полиномы степени P – 1.
Более гладкие вейвлеты создают более гладкую аппроксимацию сигнала, и наоборот – «короткие» вейвлеты лучше отслеживают пики аппроксимируемой функции. При выборе вейвлета мы также можем указать, каким должен быть уровень декомпозиции. По умолчанию PyWavelets выбирает максимальный уровень декомпозиции, возможный для входного сигнала. Максимальный уровень разложения зависит от длины входного сигнала и вейвлета:
Листинг
import pandas as pd
import pywt
filename = 'Test_set/Bearing2_3/acc_00001.csv'
df = pd.read_csv(filename, header=None)
data = df[4].values
w=['db1', 'db38']
for v in w:
n_level=pywt.dwt_max_level(len(data),v)
print('Для вейвлета %s максимальный уровень декомпозиции: %s ' %(v,n_level))Для вейвлета db1 максимальный уровень декомпозиции: 11
Для вейвлета db38 максимальный уровень декомпозиции: 5
Для полученных значений максимальных уровней декомпозиции вейвлетов рассмотрим работу фильтра по удалению высокочастотных шумов:
Листинг
import pandas as pd
import scaleogram as scg
from pylab import *
import pywt
filename = 'Test_set/Bearing2_3/acc_00001.csv'
df = pd.read_csv(filename, header=None)
signal = df[4].values
discrete_wavelets =[('db38', 5),('db1',11)]
for v in discrete_wavelets:
def lowpassfilter(signal, thresh = 0.63, wavelet=v[0]):
thresh = thresh*nanmax(signal)
coeff = pywt.wavedec(signal, wavelet, mode="per" )
coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:])
reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" )
return reconstructed_signal
wavelet = pywt.DiscreteContinuousWavelet(v[0])
phi, psi, x = wavelet.wavefun(level=v[1])
fig, ax = subplots(figsize=(8,4))
ax.set_title("График первообразной функции вейвлета: %s,level=%s"%(v[0],v[1]), fontsize=12)
ax.plot(x,phi,linewidth=2)
fig, ax = subplots(figsize=(8,4))
ax.plot(signal, color="b", alpha=0.5, label=' Оригинальный сигнал ')
rec = lowpassfilter(signal, 0.4)
ax.plot(rec, 'r', label='DWT преобразование сигнала', linewidth=2)
ax.legend()
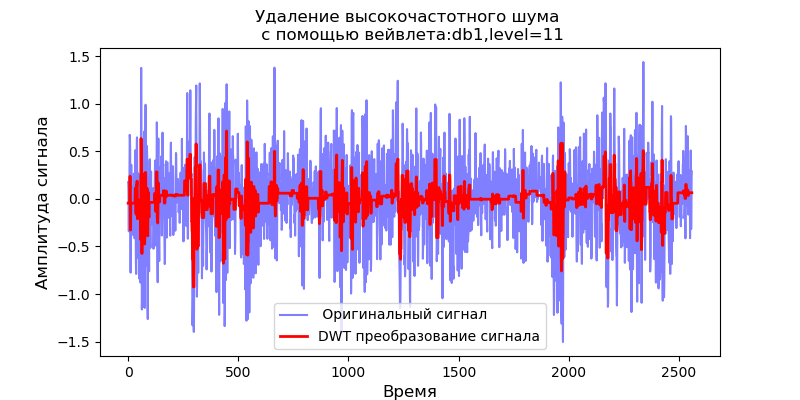
ax.set_title('Удаление высокочастотного шума \n с помощью вейвлета:%s,level=%s'%(v[0],v[1]),fontsize=12)
ax.set_ylabel('Амплитуда сигнала', fontsize=12)
ax.set_xlabel('Время', fontsize=12)
wavelet = 'cmor1-0.5'
ax = ax = scg.cws(rec, scales=arange(1,128), wavelet=wavelet,figsize=(8, 4), cmap="jet", ylabel='Период ', xlabel="Время ", yscale="log",
title='CWT сигнала \n(спектр мощности после DWT фильтрации )')
show()

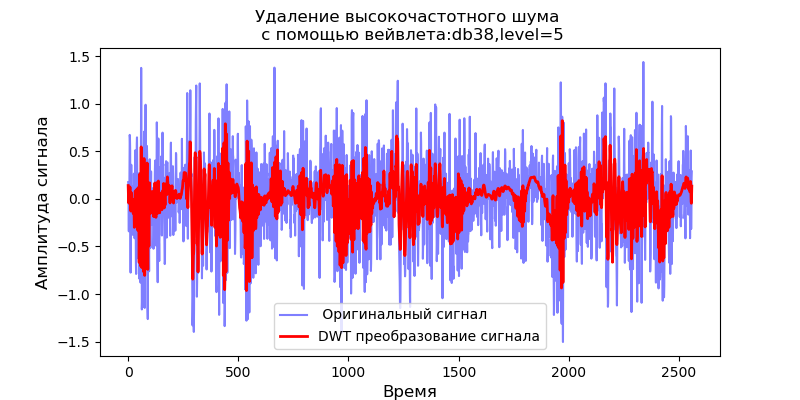
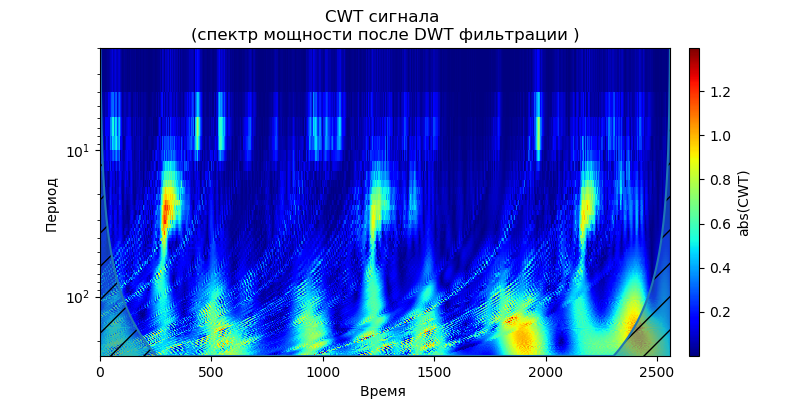


Из приведенных скалограмм сигналов на выходе фильтра следует, что для вейвлета db38 за пиками мощности спектра следуют локализованные области, для вейвлета db1 эти области исчезают.Можно выбрать вейвлет, первообразная функция которого будет иметь форму, характерную для явлений, которые мы ожидаем увидеть. Необходимо отметить, что, например, вейвлет db38 может аппроксимировать сигнал полиномом 37 степени. Это расширяет возможности классификации сигналов, например, для выявления неисправностей оборудования по сигналам датчиков вибрации.
Поскольку сигнал после фильтра с вейвлетом Добеши образует временной ряд используя коэффициенты апроксимации и декомпозиции как характеристики ряда можно определять степень близости таких рядов, что существенно упрощает их поиск и классификацию
Фильтр Калмана для удаления высокочастотного шума
Фильтр Калмана широко используется для фильтрации шума в различных динамических системах. Рассмотрим динамическую систему с вектором состояния x.
где F — матрица переходов (transition matrix),
w(Q) — случайный процесс (шум) с нулевым математическим ожиданием и матрицей ковариаций Q.
Будем наблюдать переходы состояний системы с известной погрешностью измерений в каждый момент времени. Удаление шума с помощью метода Калмана состоит из двух шагов — экстраполяция и коррекция, выглядит это следующим образом.
Зададим параметры системы:
Q- матрицей ковариаций шума (process noise covariance ).
H — матрица наблюдения (measurement).
R — ковариация шума наблюдения (measurement noise covariance).
P =Q — начальное значение ковариационной матрицы для вектора состояния.
z(t) — наблюдаемое состояние системы.
x= z(0) — начальное значение оценки состояния системы.
Для каждого наблюдения z будем вычислять отфильтрованное состояние x
и для этого выполняем следующие шаги.
• шаг 1: экстраполяция
1. экстраполяция (предсказание) состояния системы
2. вычисляем ковариационную матрицу для экстраполированного вектора состояния
• шаг 2: коррекция
1. вычисляем вектор ошибки, отклонение наблюдения от ожидаемого состояния
2. вычисляем ковариационную матрицу для вектора отклонения (вектора ошибки)
3. вычисляем коэффициенты усиления Калмана
4. коррекция оценки вектора состояния
5. корректируем ковариационную матрицу оценки вектора состояния системы
Листинг для реализации алгоритма
from scipy import*
from pylab import*
import pandas as pd
def kalman_filter( z,
F = eye(2), # матрица перехода состояний системы (transitionMatrix)
Q = eye(2)*3e-3, # ковариация шума (processNoiseCov)
H = eye(2), # матрица наблюдения (measurement)
R = eye(2)*3e-1 # ковариация шума наблюдения (measurementNoiseCov)
):
n = z.shape[0] # количество элементов
#m = z.shape[1] # размерность пространства
x = z[0,:].transpose() # начальное значение предсказания состояния системы
P = Q # ковариационная матрица для экстраполированного вектора состояния
r = [ x ] # результат
for i in range(1,n):
# экстраполяция:
x = F.dot( x ) # экстраполяция (предсказание) состояния системы
P = F.dot(P).dot( F.transpose() ) + Q # ковариационная матрица для экстраполированного вектора состояния
# коррекция:
y = z[i] - H.dot(x) # вектор ошибки, отклонение фактического наблюдения от ожидаемого (экстраполированного) наблюдения
S = H.dot(P).dot(H.transpose()) + R # ковариационная матрица для вектора отклонения (вектора ошибки)
K = P.dot(H.transpose()).dot(linalg.inv(S)) # матрица коэффициентов усиления Калмана
x = x + K.dot(y) # коррекция оценки вектора состояния
P = ( eye(z.shape[1]) - K.dot(H) ).dot(P) # ковариационная матрица оценки вектора состояния системы
r.append( x.transpose())
return array(r)
filename = 'Test_set/Bearing2_3/acc_00001.csv'
df = pd.read_csv(filename, header=None)
signal = df[4].values
N= signal .shape[0] # длина последовательности
# 2 dimensions
y0 =linspace(0.0,2500.0,N)
y1 =signal
d = array(list(zip(y0,y1)))
dn = d
r = kalman_filter(dn)
fig, ax = subplots(figsize=(8,4))
ax.plot( d[:,0], d[:,1],'b', label='Оригинальный сигнал' )
ax.plot( r[:,0], r[:,1],'r', label='kalman' )
ax.legend(loc='upper left')
ax.set_title('Удаление высокочастотного шума с помощью фильтра Калмана \n (расчёт по алгоритму)', fontsize=12)
ax.set_ylabel('Амплитуда сигнала', fontsize=12)
ax.set_xlabel('Время', fontsize=12)
show()
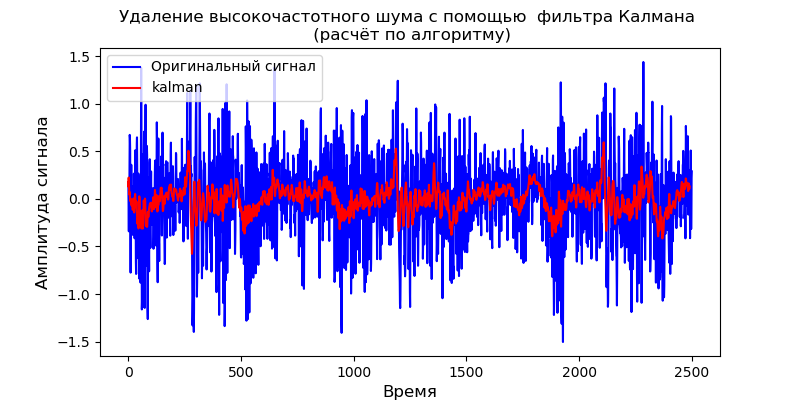
Для приведенной динамической модели можно использовать и библиотеку pyKalman:
Листинг
from pykalman import KalmanFilter
import pandas as pd
from pylab import *
import scaleogram as scg
filename = 'Test_set/Bearing2_3/acc_00001.csv'
df = pd.read_csv(filename, header=None)
signal = df[4].values
measurements =signal
kf = KalmanFilter(transition_matrices=[1] ,# A матрица перехода состояний между временами t и t+1
observation_matrices=[1],# C матрица наблюдения
initial_state_mean=measurements[0],#среднее начальное состояние
initial_state_covariance=[1],#ковариация начального состояния распределение
observation_covariance=[1],# R ковариационная матрица наблюдения
transition_covariance= 0.01) # Q ковариационная матрица перехода состояний
state_means, state_covariances = kf.filter(measurements)#среднее начальное, начальная ковариация
state_means=[w[0] for w in state_means]
state_std = sqrt(state_covariances[:,0])
fig, ax = subplots(figsize=(8,4))
ax.plot(measurements ,'b', label='Оригинальный сигнал')
ax.plot(state_means ,'r', label='kalman-выход фильтра')
ax.legend()
ax.set_title('Удаление высокочастотного шума с помощью фильтра Калмана\n (библиотека pyKalman)', fontsize=14)
ax.set_ylabel('Амплитуда сигнала', fontsize=12)
ax.set_xlabel('Время', fontsize=12)
wavelet = 'cmor1-0.5'
ax = ax = scg.cws(signal, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4),cmap="jet", ylabel='Период ', xlabel="Время ", yscale="log",
title='CWT сигнала до фильтра Калмана\n(спектр мощности)')
ax = ax = scg.cws(state_means, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4), cmap="jet", ylabel='Период ', xlabel="Время ", yscale="log",
title='CWT сигнала после фильтра Калмана \n(спектр мощности )')
show()



Фильтр Калмана хорошо удаляет высокочастотный шум однако не позволяет менять форму выходного сигнала.
Метод скользящего среднего
При определении основного направления изменений сильно осциллирующей последовательности возникает задача её сглаживания методом скользящего среднего. Это могут быть показания датчика уровня топлива в автомобиле или, как в нашем случае, данные высокочастотных датчиков относительно ускоренной деградации подшипников. Задачу можно рассматривать, как восстановление некоторой последовательности r, на которую был наложен шум.
Простое скользящее среднее сокращённо — SMA (Simple Moving Average). Для вычисления текущего значения фильтра мы просто усредняем предыдущие n элементов последовательности, соответственно фильтр начинает работать с элемента последовательности n.
Листинг
<source lang="python">from scipy import *
import pandas as pd
from pylab import *
import pywt
import scaleogram as scg
def get_ave_values(xvalues, yvalues, n = 6):
signal_length = len(xvalues)
if signal_length % n == 0:
padding_length = 0
else:
padding_length = n - signal_length//n % n
xarr = array(xvalues)
yarr = array(yvalues)
xarr.resize(signal_length//n, n)
yarr.resize(signal_length//n, n)
xarr_reshaped = xarr.reshape((-1,n))
yarr_reshaped = yarr.reshape((-1,n))
x_ave = xarr_reshaped[:,0]
y_ave = nanmean(yarr_reshaped, axis=1)
return x_ave, y_ave
def plot_signal_plus_average(time, signal, average_over = 5):
fig, ax = subplots(figsize=(8, 4))
time_ave, signal_ave = get_ave_values(time, signal, average_over)
ax.plot(time_ave, signal_ave,"b", label = 'Скользящее среднее сигнала (n={})'.format(5))
ax.set_xlim([time[0], time[-1]])
ax.set_ylabel('Амплитуда сигнала', fontsize=12)
ax.set_title('Фильтрация сигнала методом скользящего среднего SMA', fontsize=14)
ax.set_xlabel('Время', fontsize=12)
ax.legend()
return signal_ave
filename = 'Test_set/Bearing2_3/acc_00001.csv'
df = pd.read_csv(filename, header=None)
df_nino = df[4].values
N = df_nino.shape[0]
time = arange(0, N)
signal = df_nino
signal_ave=plot_signal_plus_average(time, signal)
wavelet = 'cmor1-0.5'
ax = ax = scg.cws(signal, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4),cmap="jet", ylabel='Период ', xlabel="Время ", yscale="log",
title='CWT сигнала %s \n(спектр мощности до фильтрации МСС )'%filename)
ax = ax = scg.cws(signal_ave, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4), cmap="jet", ylabel='Период ', xlabel="Время ", yscale="log",
title='CWT сигнала %s \n(спектр мощности после фильтрации МСС)'%filename)
show()

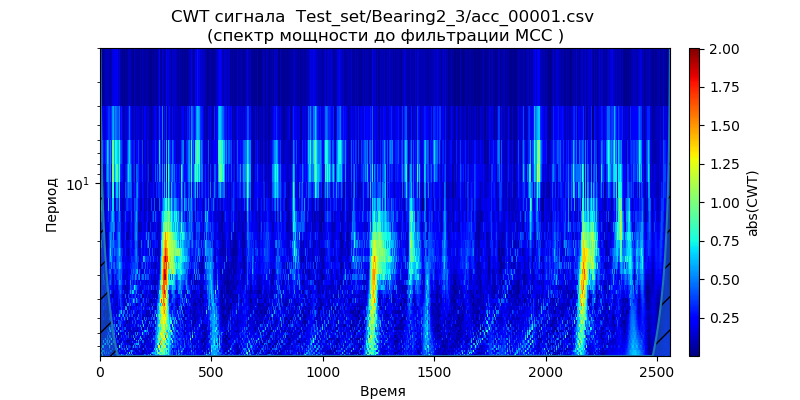

Как следует из скалограммы метод SMA плохо очищает сигнал от высокочастотного шумма, и
как было указано выше используется для сглаживания.
Выводы:
- С использованием модуля scaleogram получены CWT вейвлет скалограммы трёх тестовых сигналов вибродатчика для разных условий испытаний подшипников одного типа. По данным скалограмм выбран сигнал с явно выраженными признаками поздней деградации. Этот сигнал использован для демонстрации работы фильтров во всех приведенных примерах.
- Рассмотрены методы библиотеки PyWavelets для DWT деконструкции и восстановления сигнала вибродатчика с применением модулей pywt.dwt(), pywt.idwt() и модуля pywt.wavedec() для заданого уровня вейвлета.
- На примерах рассмотрены особенности применения модуля pywt.threshol() фильтрации коэффициентов DWT детализации, отвечающих за высокочастотную часть спектра с помощью пороговых функций при заданной величине порога.
- Рассмотрены влияния первообразной DWT вейвлета на форму сигнала, очищенного от шумов.
- Получена модель фильтра Калмана для динамической среды, модель проверена на тестовом сигнале вибродатчика. График удаления шума совпадает с аналогичным графиком, полученным с использованием модуля pyKalman. Характер графика совпадает со скалограммой.
- Рассмотрен метод удаления шума из сигнала на основе скользящего среднего.