Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Под капотом почти каждой поисковой строки бьется одно и то же пламенное сердце — инвертированный индекс. Именно инвертированный индекс принимает текстовые запросы и возвращает пользователю список документов, а пользователь смотрит на всё это дело и радуется котиками, ответам с StackOverflow и страничкам на вики.
В статье описано устройство поиска, инвертированного индекса и его оптимизаций с отсылками к теории. В качестве подопытного кролика взят Tantivy — реализация архитектуры Lucene на Rust. Статья получилась концентрированной, математикосодержащей и несовместимой с расслабленным чтением хабра за чашкой кофе, осторожно!
Формальная постановка задачи: есть набор текстовых документов, хотим быстро находить в этом наборе наиболее подходящие документы по поисковому запросу и добавлять в набор новые документы для последующего поиска.
Первым шагом определим что такое релевантность документа запросу, причем сделаем это способом, понятным компьютеру. Вторым шагом
Определение релевантности
На человеческом языке «релевантность» — это смысловая близость документа к запросу. На языке математики близость может выражаться через близость векторов. Поэтому для математического выражения релевантности необходимо документам и запросам из мира людей сопоставить вектора в некотором пространстве из мира математики. Тогда документ будет считаться релевантным запросу, если документ-вектор и запрос-вектор в нашем пространстве находятся близко. Поисковая модель с таким определением близости зовётся векторной моделью поиска.
Основной проблемой в векторной модели поиска является построение векторного пространства и преобразования документов и запросов в . Вообще говоря, векторные пространства и преобразования могут быть любыми, лишь бы близкие по смыслу документы или запросы отображались в близкие вектора.
Современные библиотеки позволяют по щелчку пальцев конструировать сложные векторные пространства с небольшим количеством измерений и высокой информационной нагрузкой на каждое измерение. В таком пространстве все координаты вектора характеризуют тот или иной аспект документа или запроса: тему, настроение, длину, лексику или любую комбинацию этих аспектов. Зачастую то, что характеризует координата вектора, невыразимо на человеческом языке, зато понимается машинами. Нехитрый план построения такого поиска:
- Берем любимую библиотеку построения эмбеддингов для текстов, например fastText или BERT, преобразуем документы в вектора
- Складываем полученные вектора в любимую библиотеку для поиска K ближайших соседей (k-NN) к данному вектору, например в faiss
- Поисковый запрос преобразовываем в вектор тем же методом, что и документы
- Находим ближайшие вектора к запросу-вектору и извлекаем соответствующие найденным векторам документы
Поиск, основанный на k-NN, будет очень медленным, если вы попытаетесь засунуть в него весь Интернет. Поэтому мы сузим определение релевантности так, чтобы всё стало вычислительно проще.
Мы можем считать более релевантными те документы, в которых больше совпавших слов со словами из поискового запроса. Или в которых встречаются более «важные» слова из запроса. Именно вот такие выхолощенные определения релевантности использовались первыми людьми при создании первых масштабных поисковых систем.
NB.: Здесь и далее «слова» в контексте документов и запросов будут называться «термами» с целью избежания путаницы
Запишем релевантность в виде двух математических функций и далее будем наполнять их содержанием:
- — релевантность документа запросу
- — релевантность документа одному терму
На наложим ограничение аддитивности и выразим релевантность запроса через сумму релевантностей термов: Аддитивность упрощает дальнейшие вычисления, но вынуждает нас согласиться с сильным упрощением реальности — будто бы все слова в тексте встречаются независимо друг от друга.
Наиболее известные аддитивные функции релевантности — TF-IDF и BM25. Они используются в большинстве поисковых систем как основные метрики релевантности.
Откуда взялись TF-IDF и BM25
Если вы знаете как выводятся формулы из заголовка, то эту часть можно пропустить.
И TF-IDF, и BM25 показывают степень релевантности документа запросу одним числом. Чем выше значение метрик, тем более релевантен документ. Сами по себе значения не имеют какой-либо значимой интерпретации. Важно только сравнение значений функций для различных документов. Один документ более релевантен данному запросу, чем другой, если значение его функции релевантности выше.
Попробуем повторить рассуждения авторов формул и воспроизвести этапы построения TF-IDF и BM25. Обозначим размер корпуса проиндексированных документов как . Самое простое, что можно сделать — это определить релевантность равной количеству вхождений терма (termFrequency или ) в документ: Что делать, если у нас не один терм , а запрос , состоящий из нескольких термов, и мы хотим посчитать запроса для этого документа? Вспоминаем про ограничение аддитивности и просто суммируем все отдельные по термам из запроса: В формуле выше есть проблема — мы не учитываем различную «важность» разных термов. Если у нас будет запрос «cat and dog», то наиболее релевантными окажутся документы, в которых есть 100500 вхождений терма «and». Вряд ли это то, что хотел бы получить пользователь.
Исправляем проблему, взвешивая каждый терм в соответствии с его важностью: — это количество документов в корпусе, содержащих терм . Получается, что чем чаще терм встречается, тем менее он важен и тем меньше будет . Термы вроде «and» будут иметь огромный и соответственно маленький .
Вроде уже лучше, но теперь есть другая проблема — сам по себе мало о чём говорит. Если , и размер корпуса проиндексированных текстов — 100 документов, то терм «жираф» в этом случае считается очень частым. А если размер корпуса 100 000, то уже редким.
Зависимость от может быть убрана превращением в относительную частоту путем деления на : Теперь представим следующее — у нас 100 документов, в одном из них есть терм «слон», в двух — «жираф». в первом случае будет равно 100, а во-втором — 50. Терм «жираф» получит в два раза меньше очков, чем терм «слон» только лишь потому, что документов с жирафом на один больше, чем со слоном. Исправим эту ситуацию, сгладив функцию .
Сглаживание можно произвести различными способами, мы сделаем это логарифмированием: Мы только что получили TF-IDF. Едем дальше к BM25.
Вряд ли документ, содержащий терм «жираф» 200 раз в два раза лучше, чем документ, содержащий терм «жираф» 100 раз. Поэтому и тут проедемся сглаживанием, только теперь сделаем это не логарифмированием, а чуть иначе. Заменим на С каждым увеличением числа вхождения терма на единицу, значение прирастает все меньше и меньше — функция сглажена. А параметром мы можем контролировать кривизну этого сглаживания. Говоря по-умному, параметр контролирует степень сатурации функции.
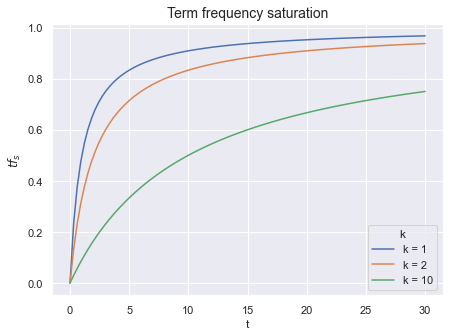
Рис. 0: Чем выше значение , тем сильнее будут учитываться последующие вхождения одного и того же терма.
У есть два замечательных побочных эффекта.
Во-первых, будет больше у документов, содержащих все слова из запроса, чем у документов, которые содержат одно слово из запроса несколько раз. Топ документов в этом случае будет больше радовать глаз и ум пользователя, ведь все термы запроса обычно печатаются не просто так.
Во-вторых, значение функции ограничено сверху. Остальная часть тоже ограничена сверху, поэтому и вся функций имеет ограничение сверху (далее — upper bound). Более того, в нашем случае очень просто посчитать.
Почему важно для нас? является максимально возможным вкладом этого терма в значение функции релевантности. Если мы знаем , то можем срезать углы при обработке запроса.
Последний шаг — начнем учитывать длину документов в . В длинных документах терм «жираф» может встретится просто по-случайности и его наличие в тексте ничего не скажет о реальной теме документа. А вот если документ состоит из одного терма и это терм «жираф», то можно совершенно точно утверждать, что документ о жирафах.
Очевидный способ учесть длину документа — взять количество слов в документе . Дополнительно поделим на среднее количество слов во всех документах . Сделаем мы это исходя из тех же соображений, из каких нормировали выше — абсолютные значения портят качество метрики.
Найдем теперь место для длины документа в нашей формуле. Когда растет, то значение падает. Если мы будем умножать на , то получится, что более длинные документы будут получать меньший . То что нужно!
Можно еще дополнительно параметризовать силу, с которой мы учитываем длину документа, для контроля поведения формулы в разных ситуациях. Заменим на и получим: При формула вырождается в , а при формула принимает вид .
Ещё раз: — сила влияния повторяющихся термов на релевантность, а — сила влияния длины документа на релевантность.
Подставим в :
У нас получилась формула BM25 с небольшим нюансом. В каноничной формуле (этот член называется ) заменен на . Замена не имеет простых эвристик под собой и основана на подгонке под теоретически более чистую форму RSJ модели. Такая форма дает меньший вес слишком часто встречающимся термам: артиклям, союзам и прочим сочетаниям букв, несущим малое количество информации.
Важное замечание: из формулы BM25 теперь видно, что в бОльшей мере зависит от значения , то есть от частоты терма в корпусе. Чем реже встречается терм, тем выше его максимально возможный вклад в .
Реализация инвертированного индекса
С учетом ограниченной памяти, медленных дисков и процессоров нам теперь нужно придумать структуру данных, способную выдавать top-K релевантных по BM25 документов.
Есть у нас набор документов, по которым необходимо вести поиск. Всем документам присваивается document ID или DID. Каждый документ разбивается на термы, термы при желании обрезаются или приводятся к каноничной форме. Для каждого обработанного терма составляется список DID документов, содержащих этот терм — постинг-лист.

Рис. 1: Постинг-листы
Различные реализации инвертированных индексов также могут сохранять точные места в документе, где встречается терм или общее количество вхождений терма в документ. Эта дополнительная информация используется при подсчете метрик релевантности или для выполнения специфичных запросов, в которых важно взаимное расположение термов в документе. Сам постинг-лист сортируется по возрастанию DID, хотя существуют и иные подходы к его организации.
Вторая часть инвертированного индекса — словарь всех термов. Под словарь используется KV-хранилище, где термы являются ключами, а значения — адреса постинг-листов в RAM или на диске. Обычно для KV-хранилища в оперативной памяти используются хеш-таблицы и деревья. Однако для словаря термов могут оказаться более подходящими другие структуры, например, префиксные деревья.

Рис. 2: Словарь термов (префиксное дерево)
В Tantivy для хранения термов вообще использованы finite-state transducers через crate fst. Если совсем упрощать, то можно считать, что префиксные деревья организуют словарь путем выделения общих префиксов у ключей, а трансдюсеры ещё могут и общие суффиксы выделять. Поэтому сжатие словаря происходит эффективнее, только в итоге получается уже не дерево, а ациклический орграф.
Библиотека fst в крайних случаях может сжимать даже лучше алгоритмов компрессии общего назначения при сохранении произвольного доступа. Крайние случаи случаются, когда большая часть ваших термов имеет длинные общие части. Например, когда вы складываете в инвертированный индекс URLы.
Ещё в fst есть методы сериализации и десериализации словаря, что сильно облегчает жизнь — складывать руками графы и деревья на диск то ещё развлечение. И в отличии от хеш-таблиц, fst позволяет использовать подстановку (wildcard) при поиске по ключам. Говорят, некоторые таинственные люди пользуются звездочкой в поисковых запросах, но я таких не видел.
Используя словарь термов и постинг-листы можно для запроса из одного одного терма определить список документов, в котором этот терм появляется. Затем останется посчитать для каждого документа из постинг-листа и взять top-K документов.
Для этого перенесем из области математики в реальный мир. В Tantivy используется BM25, как один из вариантов функции релевантности:
- — подсчитываем количество DID документа в постинг-листе терма , либо храним отдельным числом, что ускорит весь процесс за счет использования дополнительной памяти. Tantivy использует последний вариант: упаковывает DID в блоки по 128 чисел, а затем пишет блок из 128 частот термов, используя bitpack-кодировку
- — длина всего постинг-листа
- — рассчитываем на основе двух статистик, общего количества документов в индексе и суммарной длины всех постинг-листов. Обе статистики поддерживаются инвертированным индексом в актуальном состоянии при добавлении нового документа
- — храним для каждого документа в отдельном списке
Кроме словаря термов, постинг-листов и длин документов Tantivy (и Lucene) сохраняет в файлах:
- Точные позиции слов в документах
- Скип-листы для ускорения итерирования по спискам (об этом дальше)
- Прямые индексы, позволяющие извлечь сам документ по его DID. Работают прямые индексы медленно, так как документы хранятся сжатыми тяжелыми кодеками типа brotli
- FastFields — встроенное в инвертированный индекс быстрое KV-хранилище. Его можно использовать для хранения внешних статистик документа а-ля PageRank и использовать их при расчете вашей модифицированной функции
Теперь, когда мы можем посчитать для запроса из одного терма, найдем top-K документов. Первая идея — посчитать для всех документов их оценки, отсортировать по убыванию и взять К первых. Потребуется хранить всё в RAM и при большом количестве документов у нас кончится память.
Поэтому при обходе постинг-листа от начала и до конца первые документов кладутся в кучу (далее top-K heap) безусловно. А затем каждый последующий документ сначала оценивается и кладется в кучу только если его выше минимального из кучи. Текущий минимум в top-K heap далее будет обозначен как .
Операции над постинг-листами для запросов из нескольких термов
Что сделает инвертированный индекс с запросом «скачать OR котики»? Он заведет два итератора по постинг-листам для термов «скачать» и «котики», начнет итерирование по обоим листам, попутно рассчитывая и поддерживая top-K heap.
Аналогичным образом реализуется AND-запрос, однако тут итерирование позволяет пропускать значительные части постинг-листов без расчета для них.
Более важными для поисковиков общего назначения являются OR-запросы. А всё потому, что они покрывают больше документов и потому, что ранжирование запросов метриками TF-IDF или BM25 всё равно поднимает в топ документы с бОльшим количеством совпавших слов. Это сделает top-K документов больше похожим на результат работы AND-запроса.
Наивный алгоритм реализации OR-запроса следующий:
- Создаем итераторы для постинг-листов каждого терма из запроса
- Заводим top-K heap
- Сортируем итераторы по DID, на которые они указывают
- Берем документ, на который указывает первый итератор и собираем среди оставшихся итераторов те, которые указывают на тот же документ. Так мы получим DID и термы, которые содержатся в этом документе
- Рассчитываем релевантность документа по термам, складываем их, получаем релевантность по всему запросу. Если документ хороший, то кладем его в top-K heap
- Продвигаем использованные итераторы и возвращаемся к п.3

Рис. 3: Итерации OR-алгоритма. Чуть ниже есть псевдокод алгоритма
В п.4 сбор итераторов осуществляется быстро, так как список итераторов отсортирован по DID. Пересортировку итераторов в п.3 тоже можно оптимизировать, если мы знаем какие итераторы были продвинуты в п.6.
Некоторые оптимизации инвертированного индекса
В обычной задаче поиска ищутся не вообще все релевантные документы, а только K наиболее релевантных. Это открывает путь для важных оптимизаций. Причина простая — большая часть документов станет ненужной и мы избежим накладных вычислений над ней. Такая постановка задачи ещё известна как Top-K queries.
Посмотрим внимательнее на псевдокод OR-алгоритма Bortnikov, 2017:
Input:
termsArray - Array of query terms
k - Number of results to retrieve
Init:
for t ∈ termsArray do t.init()
heap.init(k)
θ ← 0
Sort(termsArray)
Loop:
while (termsArray[0].doc() < ∞) do
d ← termsArray[0].doc()
i ← 1
while (i < numTerms ∩ termArray[i].doc() = d) do
i ← i + 1
score ← Score(d, termsArray[0..i − 1]))
if (score ≥ θ) then
θ ← heap.insert(d, score)
advanceTerms(termsArray[0..i − 1])
Sort(termsArray)
Output: return heap.toSortedArray()
function advanceTerms(termsArray[0..pTerm])
for (t ∈ termsArray[0..pTerm]) do
if (t.doc() ≤ termsArray[pTerm].doc()) then
t.next()
Наивный алгоритм работает с асимптотикой , где L — суммарная длина используемых при обработке запроса постинг-листов, а Q — количество слов в запросе. Немного обнаглев, из оценки можно выкинуть — подавляющее большинство пользователей приносит запросы не длиннее какого-то максимума и можно считать константой.
На практике, наибольший вклад в скорость работы инвертированного индекса вносит размер корпуса (т.е длины постинг-листов) и частота запросов. Включенное автодополнение запроса или внутренние аналитические запросы в поисковую систему способны кратно умножить нагрузку на систему. Даже в такой ситуации оказывается слишком грустной оценкой.
Сжатие постинг-листов
Размер постинг-листов может достать гигабайтных размеров. Хранить постинг-листы как есть и бегать вдоль них без выдоха — плохая идея. Во-первых, можно не влезть в диск. Во-вторых, чем больше надо читать с диска, тем всё медленнее работает. Поэтому постинг-листы являются первыми кандидатами на сжатие.
Вспомним, что постинг-лист — это возрастающий список DID, сами DID — обычно 64-битные беззнаковые числа. Числа в постинг-листе не сильно отличаются друг от друга и лежат в достаточно ограниченной области значений от 0 до некоторого числа, сопоставимого с количеством документов в корпусе.
VarLen Encoding
Странно тратить 8 байт на то, чтобы закодировать маленькое число. Поэтому люди придумали коды, представляющие маленькие числа при помощи малого числа байт. Такие схемы называются кодировками с переменной длиной. Нас будет интересовать конкретная схема, известная под названием varint.
Чтение числа в varint происходит байт за байтом. Каждый прочитанный байт хранит сигнальный бит и 7 бит полезной нагрузки. Сигнальный бит говорит о том, нужно ли нам продолжать чтение или текущий байт является для этого числа последним. Полезная нагрузка конкатенируется вплоть до последнего байта числа.
Постинг-листы хорошо сжимаются varint'ом в несколько раз, но теперь у нас связаны руки — прыгнуть вперед в постинг-листе через N чисел нельзя, ведь непонятно где границы каждого элемента постинг-листа. Получается, что читать постинг-лист мы можем только последовательно, ни о какой параллельности речи не идет.
SIMD
Для возможности параллельного чтения изобрели компромиссные схемы, похожие на varint, но не совсем. В таких схемах числа разбиваются на группы по N чисел и каждое число в группе кодируются одинаковым количеством бит, а вся группа предваряется дескриптором, описывающим что в группе находится и как это распаковать. Одинаковая длина запакованных чисел в группе позволяет использовать SIMD-инструкции (SSE3 в Intel) для распаковки групп, что кратно ускоряет время работы.
Delta-encoding
Varint хорошо сжимает малые числа и хуже сжимает большие числа. Так как в постинг-листе находятся возрастающие числа, то с добавлением новых документов качество сжатия будет становиться хуже. Простое изменение — в постинг-листе будем хранить не сами DID, а разницу между соседними DID. Например, вместо [2, 4, 6, 9, 13] мы будем сохранять [2, 2, 2, 3, 4].
Список всё постоянно возрастающих чисел превратится в список небольших неотрицательных чисел. Сжать такой список можно эффективнее, однако теперь для раскодирования i-го числа нам нужно посчитать сумму всех чисел до i-го. Впрочем, это не такая уж и большая проблема, ведь varint и так подразумевает, что чтение списка будет последовательным.
Скип-листы для итерирования по постинг-листам
После сжатия постинг-листов, массив чисел превращается в связанный список. Всё, что мы теперь можем сделать — это последовательно обходить список от начала к концу. Хотя до сих пор нам большего и не требовалось, описанные в следующих секциях схемы оптимизации нуждаются в возможности продвигать итераторы на произвольное число DID вперед.
Есть такая замечательная штука — скип-листы. Скип-лист живет рядом со связанным списком чисел и представляет из себя разреженный индекс по содержанию этого списка. Если вы хотите в списке чисел найти Х, то скип-лист за время пояснит вам, куда именно надо прыгнуть, чтобы оказаться в вашем связанном списке примерно в нужном месте перед Х. После прыжка вы уже обычным линейным поиском идете до Х.
Точность прыжка зависит от объема памяти, который мы можем выделить под скип-лист — типичный компромисс в алгоритмах. В Tantivy перемещение вдоль постинг-листа реализовано именно скип-листами. Известна lock-free реализация скип-листа, но на момент написания статьи (март 2021) библиотека выглядит не слишком поддерживаемой.
В нашей реализации скип-листа нужно ещё хранить частичные суммы до того места, куда мы собираемся прыгнуть, иначе ничего не получится, потому что для постинг-листа мы использовали Delta-encoding.
Оптимизации OR-запросов
Все оптимизации обхода постинг-листов делятся на безопасные и небезопасные. В результате применения безопасных оптимизаций top-K документов остается без изменений по сравнению с наивным OR-алгоритмом. Небезопасные оптимизации могут дать большой выигрыш по скорости, но они меняют top-K и могут пропустить некоторые документы.
MaxScore
MaxScore одна из первых известных попыток ускорить выполнение OR-запросов. Оптимизация относится к безопасным, описана в Turtle, 1995.
Суть оптимизации в разбиении термов запроса на два непересекающихся множества: «обязательных» и «необязательных». Документы, содержащие термы только из «необязательного» множества, не могут войти в top-K и поэтому их постинг-листы могут быть промотаны вперед до первого документа, который содержит хотя бы один «обязательный» терм.
Помните терма, введеный в разделе про TF-IDF и BM25? Напоминаю, что это максимально возможный вклад терма в релевантность любого запроса. является функцией от и рассчитывается на лету.
Имея на руках , можно отсортировать все термы из запроса по убыванию их и посчитать частичные суммы от первого и до последнего терма. Все термы с частичной суммой меньше текущего можно отнести к «необязательному» множеству. Документ, содержащий термы только из «необязательного» множества не может быть оценен выше, чем сумма этих документов. Стало быть, такой документ не войдет в итоговое множество.
Имеет смысл рассматривать только те документы, которые содержат хотя бы один терм из «обязательного» множества термов. Поэтому мы можем промотать постинг-листы «необязательных» термов до наименьшего из DID'ов, на которые указывают итераторы «обязательных» термов. Тут-то нам и нужны скип-листы, без них пришлось бы бежать по постинг-листам последовательно и никакого выигрыша в скорости не получилось бы.

Рис. 4: Промотка итераторов в MaxScore
После каждого обновления top-K heap производится перестроение двух множеств и алгоритм завершает работу в момент, когда все термы оказываются в «необязательном» множестве.
Weak AND (WAND)
WAND также является безопасным методом оптимизации поиска, описанным в Broder, 2003. В чем-то он похож на MaxScore: также анализирует частичные суммы и .
- Все итераторы термов WAND сортирует в порядке DID, на который указывает каждый итератор
- Рассчитываются частичные суммы
- Выбирается pivotTerm — первый терм, чья частичная сумма превосходит
- Проверяются все предшествующие pivotTerm'у итераторы.
Если они указывают на один и тот же документ, то этот документ теоретически может входить в top-K документов и поэтому для него производится полноценный рассчет .
Если хотя бы один из итераторов указывает на DID, меньший чем pivotTerm.DID, то такой итератор продвигается вперед до DID, большего чемpivotTerm.DID.
После этого, мы возвращаемся на первый шаг алгоритма
Block-max WAND (BMW)
BMW является расширением алгоритма WAND из предыдущего пункта, предложенным в Ding, 2011. Вместо использования глобальных для каждого терма, мы теперь разбиваем постинг-листы на блоки и сохраняем отдельно для каждого блока. Алгоритм повторяет WAND, но проверяет в дополнение еще и частичную сумму блоков, на которые сейчас указывают итераторы. В случае, если эта сумма ниже , то блоки пропускаются.
Блочные оценки термов в большинстве случаев гораздо ниже глобальных . Поэтому многие блоки будут скипнуты и это позволит сэкономить время на расчете документов.
Для понимания разрыва между продакшеном инвертированных индексов и академическими исследованиями можно занырнуть в широко известный в узких кругах тикет LUCENE-4100.
TLDR: Реализация важной Block-max WAND-оптимизации молчаливо дожидалась смены TF-IDF на BM25, заняла 7 лет и была выкачена только в Lucene 7.
Block Upper Scoring
Рядом с для блока можно хранить другие метрики, помогающие принять решение не трогать этот блок. Либо сам поправить нужным образом так, чтобы его значение отражало вашу задумку.
Автор статьи экспериментировал с поиском, в котором необходимы были только свежие документы-новости. BM25 была заменена на где — функция, накладывающая пенальти на устаревающие документы и принимающая значения от 0 до 1. Поменяв формулу для , удалось добиться пропуска 95% всех блоков с несвежими новостями, что сильно ускорило конкретно этот вид поиска. Сам подход с хранением поблочных метрик, а также вычислимым и конечным пределом функции релевантности располагает к экспериментам.
Предварительная обработка поискового запроса
После попадания в поисковую строку и перед при приземлением в инвертированный индекс запрос проходит несколько этапов обработки.
Разбор поискового запроса

Рис. 5: Этапы обработки поискового запроса
Сначала происходит построение синтаксического дерева запроса. Из запроса выкидывается пунктуация, текст приводится к нижнему регистру, токенизируется, может использоваться стемминг, лемматизация и выкидывание стоп-слов. Из потока токенов дальше строится логическое дерево операций.
Будут ли токены соединены по умолчанию оператором OR или AND зависит от настроек индекса. С одной стороны — соединение через AND иногда может дать более точный результат, с другой — есть риск вообще ничего не найти. Можно составить несколько запросов и после их выполнения на основе размера выдачи или внешних метрик выбрать лучший вариант.
Логическое дерево ложится в основу плана операций. В Tantivy соответствующая структура называется Scorer. Реализация Scorer является центром вселенной инвертированных индексов, так как эта структура ответственна за итерирование постинг-листов и за все возможные оптимизации этого процесса.
Этап расширения поискового запроса
Пользователь практически всегда хочет получить не то, что он запрашивает, а что-то немного другое. И поэтому крупные поисковики имеют сложные системы, цель которых — расширить ваш запрос дополнительными термами и конструкциями.
Запрос разбавляется синонимами, термам добавляются веса, используется история предыдущих поисков, добавляются фильтры, контекст поиска и миллион других хаков, являющихся коммерческими секретами. Этот этап работы называется query extension, он невероятно важен для улучшения качества поиска.
На этапе расширения поисковых запросов дешево проводить эксперименты. Представьте, что вы хотите выяснить, даст ли вам какой-либо профит использование морфологии при поиске. Морфология в этом контексте — приведение разных словоформ к каноничной форме (лемме).
Например:
скачивать, скачать, скачал, скачали -> скачать
котики, котиков, котикам -> котикУ вас есть несколько вариантов:
- Тяжелый: сразу попытаться научить инвертированный индекс хранить и леммы, и словоформы, а также научиться учитывать их при поиске. Нужно много программировать и проводить переиндексацию корпуса документов.
- Компромиссный: переиндексировать весь корпус документов, приводя все словоформы к леммам на лету, а также лемматизировать приходящие запросы. Меньше программирования, но все так же требуется переиндексация.
- Простой: разбавлять запрос всеми словоформами. В таком случае запрос пользователя «скачка котиков» будет преобразован во что-то типа "(скачка^2 OR скачать OR скачивать OR скачал) AND (котиков^2 OR котики OR котик OR котикам)". Выдача будет выглядеть так, как будто бы мы умеем по-настоящему работать с леммами. Содержимое инвертированного индекса менять не требуется!
Все гипотетические затраты процессора на переиндексацию благодаря простому подходу будут перенесены на этап query extension и на обработку такого расширенного запроса. Это сэкономит вам кучу времени разработки. Fail often, fail fast!
Запись и сегментирование индекса
В архитектуре Lucene инвертированный индекс нарезан на сегменты. Сегмент хранит свою часть документов и является неизменяемым. Для добавления документов мы собираем в RAM новые документы, делаем commit и в этот момент документы из RAM сохраняются в новый сегмент.
Сегменты неизменяемы, потому что часть связанных с сегментом данных (скип-листы или отсортированные постинг-листы) являются неизменяемыми. К ним невозможно быстро добавить данные, так как это потребует перестроения всей структуры данных.
Сегменты могут обрабатывать запросы одновременно, поэтому сегмент является естественной единицей распараллеливания нагрузки. Сложность здесь возникает только в слиянии результатов из разных сегментов, так как нужно выполнять N-Way Merge потоков документов от каждого сегмента.
Тем не менее, много маленьких сегментов — плохо. А такое иногда случается, когда запись ведется небольшими порциями. В таких ситуациях Tantivy запускает процедуру слияния сегментов, превращая много маленьких сегментиков в один большой сегмент.
При слиянии сегментов часть данных, например сжатые документы, могут быть быстро слиты, а часть — придется перестраивать, что загрузит ваши CPU. Поэтому расписание слияний сильно влияет на общую производительность индекса при постоянной пишущей нагрузке.
Шардирование
Существует два способа распараллеливания нагрузки на инвертированный индекс: по документам или по термам.
В первом случае каждый из N серверов хранит только часть документов, но является сам по себе полноценным мини-индексом, во втором — хранит только часть термов для всех документов. Ответы шардов во втором случае требуют дополнительной нетривиальной обработки.
| По документам | По термам | |
|---|---|---|
| Нагрузка на сеть | Маленькая | Большая |
| Хранение дополнительных аттрибутов для документа | Просто | Сложно |
| Disk-seek'ов для запроса из K слов на N шардах | O(K*N) | O(K) |
Обычно нагрузка на сеть является большей проблемой, чем работа с диском. Поэтому такой подход использовал Google в своих первых индексах. В Tantivy также удобнее использовать шардирование по документам — сегменты индекса натуральным образом являются шардами и количество приседаний при реализации уменьшается во много раз.
Поскольку в инвертированном индексе перестроение сегментов является сложной операцией, лучше сразу начать использовать схемы типа Ring или Jump Consistent Hashing для снижения объемов перешардируемых документов при открытии нового шарда.
Многофазовые поиски и ранжирование
В поисковых системах обычно выделяются две части: базовые поиски и мета-поиск. Базовый поиск ищет по одному корпусу документов. Мета-поиск делает запросы в несколько базовых поисков и хитрым способом сливает результаты каждого базового поиска в единый список.
Базовые поиски условно можно поделить на одно- и двухфазовые. Выше в статье описан именно однофазовый поиск. Такой поиск ранжирует список документов вычислительно простыми метриками типа BM25, используя кучу различных оптимизаций, и в таком виде отдает пользователю.
Первая фаза двухфазовых (или даже многофазовых) поисков делает всё тоже самое. А вот на второй фазе происходит переранжирование top-K документов из первой фазы с использованием более тяжелых для вычисления метрик. Такое деление оправдано, поскольку отделяет быструю первую фазу на всем множестве документов от тяжелой второй фазы на ограниченном множестве документов.
На практике часть сложных метрик второй фазы часто со временем прорастает в первую фазу и позволяют сразу корректировать релевантность и обход постинг-листов для повышения качества финального результата.
Кстати, при шардировании индекса удобно сервера второй фазы использовать для агрегирования документов от шардов первой фазы.
Первая фаза ранжирования
Метрика соответствия документа запросу может быть очень простой, например , или чуть более сложной, например , где — статическое качество документа, а — произвольное отображение с областью значений .
Ограничение на в этом случае произрастает из-за использованных оптимизаций в индексе типа BMW, которые не позволяют модифицировать в большую сторону без изменения сохраненных блочных .
BM25 высчитывается в процессе работы с постинг-листами, а вот дополнительные члены типа должны лежать рядом с инвертированным индексом. Это первое существенное ограничение первой фазы поиска. Через функцию в общем случае проходит слишком много документов, чтобы была возможность на каждый из них бегать куда-то во внешние системы за дополнительными атрибутами документа.
В веб-поиске роль члена обычно исполняет PageRank, рассчитываемый раз в N дней на больших кластерах MapReduce. Посчитанный PageRank записывается в быстрое KV-хранилище инвертированного индекса, такое как FastFields в случае Tantivy и используется при вычислении релевантности.
Документы из других источников могут иметь другие метрики. Например, для поиска по научным статьям имеет смысл использовать импакт-фактор или индекс цитирования.
Вторая фаза ранжирования
На второй фазе ранжирования уже есть где разогнаться. На руках у вас имеется от сотен до тысяч более или менее релевантных документов, полученных из первой фазы. Всё оставшееся время до дедлайна запроса (обычно это доли секунды) можно запускать машинное обучение, грузить метрики из внешних баз и пересортировывать документы так, чтобы сделать выдачу ещё более релевантной.
Подтяните из вашей статистической базы информацию о кликах, используйте пользовательские предпочтения для создания персонализированной выдачи — развлекайтесь как можете. Вы вообще можете рассчитать что-нибудь на лету, например новую версию BM25, формула которой пришла вам в голову после пятничных возлияний. Потребуется только переобучение ранжирующей формулы или модели второй фазы с учетом новой метрики.
Этот этап работы является одним из самых увлекательных в разработке поиска и также важным для хорошего качества выдачи.
Качество поиска
Контроль качества поиска заслуживает отдельной статьи, здесь я лишь оставлю пару ссылок и дам несколько практических советов.
Основная цель контроля качества — тестирование и наблюдений за результатами выкатки новых версий индекса. Любая метрика качества должна быть аппроксимацией удовлетворенности пользователей в той или иной мере. Помните об этом, когда изобретаете что-то новое.
На начальном этапе разработки поиска любое повышение метрики качества обычно означает действительное улучшение качества поиска. Но чем ближе вы находитесь к верхней границе теоретически возможного качества, тем больше разнообразных артефактов будет всплывать при оптимизации той или иной метрики.
Вам потребуется много логов. Для расчета метрик качества поиска необходимо для каждого пользовательского запроса сохранять: список DID выдачи и значений их функции релевантности в текущей поисковой сессии, DID и позиции кликнутых документов, времена взаимодействий пользователя с поиском и идентификаторы сессий. Также можно хранить веса, характеризующие качество сессии. Так можно будет исключить сессии роботов и придать большие веса сессиям асессоров (если они у вас есть).
Далее пара метрик, с которых вам стоит начать. Они просто формулируется даже в терминах SQL-запроса, особенно если у вас что-то типа Clickhouse для хранения логов.
Success Rate
Самое первое и очевидное — нашёл ли вообще пользователь у вас хоть что-нибудь в рамках сессии.
SQL-сниппет
with 1.959964 as z
select
t,
round(success_rt + z*z/(2*cnt_sess) - z*sqrt((success_rt*(1 - success_rt) + z*z/(4*cnt_sess))/cnt_sess)/(1 + z*z/cnt_sess), 5) as success_rate__lower,
round(success_rt, 5) as success_rate,
round(success_rt + z*z/(2*cnt_sess) + z*sqrt((success_rt*(1 - success_rt) + z*z/(4*cnt_sess))/cnt_sess)/(1 + z*z/cnt_sess), 5) as success_rate__upper
from (
select
toDateTime(toDate(min_event_datetime)) as event_datetime,
$timeSeries as t,
count(*) as cnt_sess,
avg(success) as success_rt
from (
select
user_id,
session_id,
min(event_datetime) as min_event_datetime,
max(if($yourConditionForClickEvent, 1, 0)) as success
from
$table
where
$timeFilter and
$yourConditionForSearchEvent
group by
user_id,
session_id
)
group by
t,
event_datetime
)
order by
tMAP@k
Хорошее введение в MAP@k, а также в несколько других learning-to-rank метрик есть на Хабре. Скорее всего первое, что вы посчитаете из серьезных метрик. Метрика характеризует насколько хороший у вас top-K документов, где K обычно берется равным количеству элементов на странице поисковой выдачи.
SQL-сниппет
select
$timeSeries as t,
avg(if(AP_10 is null, 0, AP_10)) as MAP_10
from
(
select
session_id,
min(event_datetime) as event_datetime
from (
select
session_id,
event_datetime
from
query_log
where
$timeFilter and
$yourConditionForSearchEvent
)
group by
session_id
) search
left join
(
select
session_id,
sum(if(position_rank.1 <= 10, position_rank.2 / position_rank.1, 0))/10 as AP_10
from (
select
session_id,
groupArray(toUInt32(position + 1)) as position_array_unsorted,
arrayDistinct(position_array_unsorted) as position_array_distinct,
arraySort(position_array_distinct) as position_array,
arrayEnumerate(position_array) as rank_array,
arrayZip(position_array, rank_array) as position_rank_array,
arrayJoin(position_rank_array) as position_rank
from
query_log
where
$timeFilter and
$yourConditionForClickEvent
group by
session_id
)
group by
session_id
) click
on
search.session_id = click.session_id
group by
t
order by
tВместо заключения: Google и их первый инвертированный индекс

Рис. 6: Вот что бывает, когда программистов заставляют рисовать схемы против их воли (воспроизведение оригинальной блок-схемы из Brin, 1998)
Студенты Сергей Брин и Ларри Пейдж создали первую версию Google и проиндексировали около 24 миллионов документов в 1998 году. Скачивание документов студенты реализовали на Python, всего они запускали по 3-4 процесса паука. Один паук объедал примерно по 50 документов в секунду. Полное заполнение базы занимало 9 дней, выкачивалось под сотню ГБ данных. Сам индекс исчислялся десятками ГБ.
В Google изобрели свою собственную архитектуру инвертированного индекса, отличную от той, что будет использована через год в первых версиях Lucene. Формат индекса Google был простым как пять рублей и, как по мне, очень красивым.
Основа индекса — файлы в формате Barrel. Barrel — текстовый файл, хранящий четверки ⟨did, tid, offset, info⟩, отсортированные по ⟨did, offset⟩. В этой нотации did — id документа, tid — id терма, offset — позиция терма в документе.
В оригинальной системе было 64 таких Barrel файла, каждый из которых отвечал за свой диапазон термов (tid). Новый документ получал новый did и соответствующие четверки дописывались в конец Barrel файлов.
Набор таких Barrel файлов является прямым индексом, позволяющий достать список термов для заданного did бинарным поиском по did (файлы же отсортированы по did). Получить инвертированный индекс из прямого можно операцией обращения — берем и сортируем все файлы по ⟨tid, did⟩.

Рис. 7: Пересортировка Barrel-файлов
Всё! Ещё раз — мы пересортировываем одновременно 64 файла и получаем инвертированный индекс из прямого, так как теперь бинарным поиском можно искать уже по tid.
За форматом Barrel-файлов совершенно явно выглядывают уши MapReduce концепции, полноценно реализованной и задокументированной в работе J.Dean, 2004 позже.
О Google в общем доступе находится много вкусных материалов. Начать можно с оригинальной работы Brin, 1998 об архитектуре поиска, дальше потыкать в материалы Университета Нью-Джерси и шлифануть всё презентацией J.Dean о внутренней кухне первых версий индекса.
Представляете, приходите вы на работу, а вам говорят, что весь следующий год каждый месяц вам нужно будет ускорять код на 20%, чтобы дебит с кредитом сошлись. Так жил Google в начале нулевых годов. Разработчики в компании уже до того доигрались, что насильно переселяли файлы индекса на внешние цилиндры HDD — у них линейная скорость вращения выше была и файлы считывались быстрее.
К счастью, в 2021 году такие оптимизации уже не особо нужны. HDD практически вытеснены из оперативной работы, а индекс, начиная с середины 2010-ых, целиком размещается в RAM.
Дополнительная литература:
- The anatomy of a large-scale hypertextual Web search engine Brin, 1998
- Как работают поисковые системы iseg
- Compression, SIMD, and Postings Lists Trotman, 2014
- Query evaluation: Strategies and optimizations Turtle, 1995
- Efficient query evaluation using a two-level retrieval process Broder, 2003
- Faster top-k document retrieval using block-max indexes Ding, 2011




