Увидеть своими глазами: вселенная и Большой взрыв

Метаматериалы — композиты со структурными элементами, размерами много меньше длины волны излучения, обладают не только необычными свойствами, такими как отрицательный коэффициент преломления, но и способностью имитировать космологические уравнения. Они открывают новые возможности старым добрым аналоговым компьютерам. А чем хороши аналоговые вычисления? Результат виден практически сразу. Итак, на картинке ниже мы видим… Большой взрыв! Читаем, как это получилось.

Большой взрыв и путешествия во времени

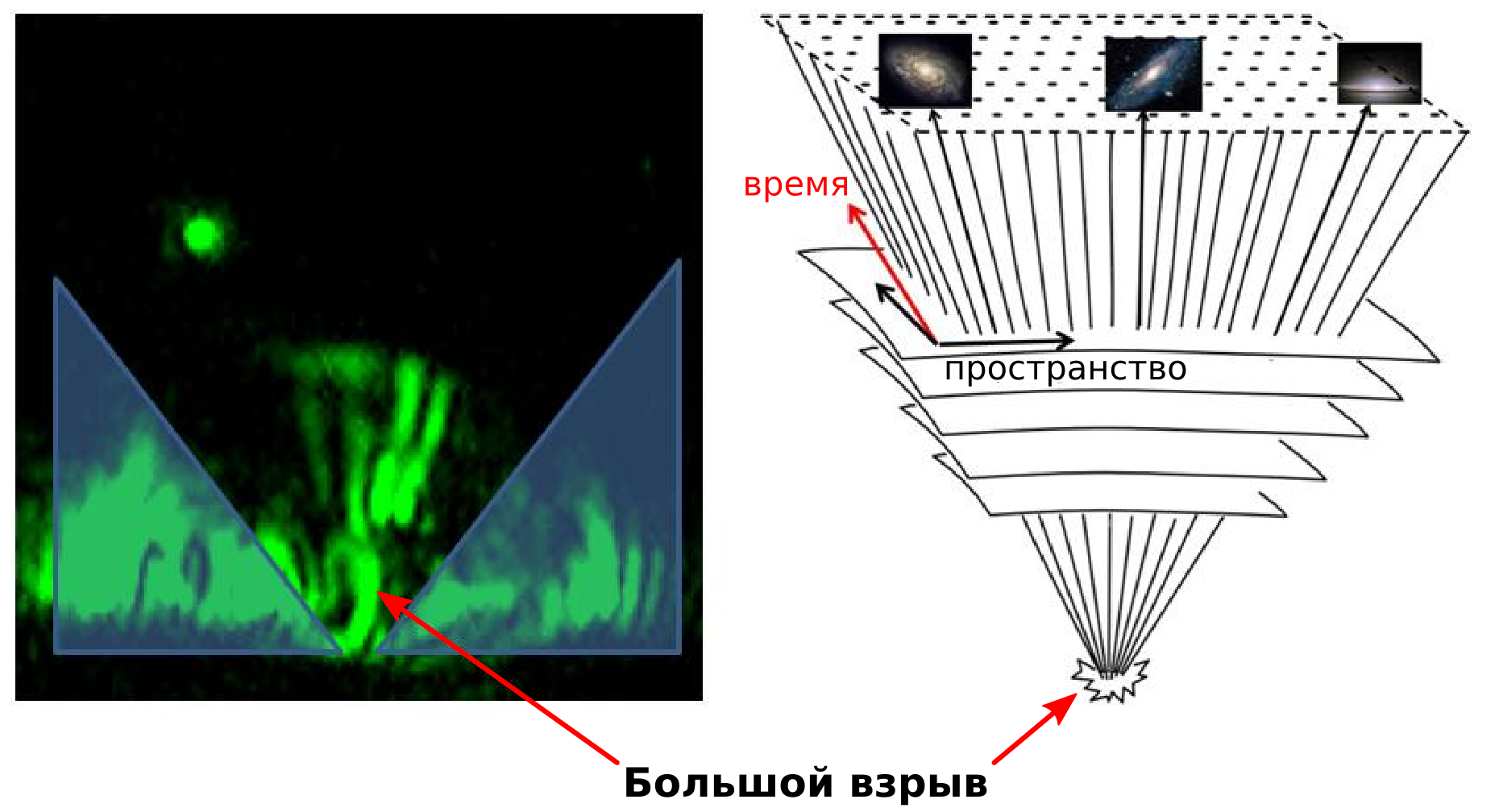
В своём исследовании, Игорь Смолянинов и Юй-Юу Хунг из Университета Мэриленда построили метаматериал путем нанесения на золотую подложку полосок оргстекла. Математическое описание поведения электромагнитных волн в метаматериале имеет много общего с общей теорией относительности (далее ОТО), которая описывает пространство-время. Следовательно, путь распространения света в метаматериале аналогичен пути массивной частицы в (2+1)-размерном пространстве-времени.

В немагнитном анизотропном материале с диэлектрическими константами $$ и $$ волна с компонентой $$ согласно уравнениям Максвелла:

У метаматериала с $$ и $$ это уравнение можно переписать в форме уравнения Клейна-Гордона:

для массивного скалярного поля. Тогда координата $$ в уравнении Максвелла подобна времени $$ в уравнении Клейна-Гордона. При освещении метаматериала лазером, появляющийся световой узор представляет собой историю (2+1)-мерного пространства-времени, населённого частицами с массой $$. Этот узор составлен из мировых линий частиц, живущих в двумерном пространстве $$ и временем $$.

Расположение полосок концентрическими окружностями, а не параллельными полосками, приводит к уравнению в цилиндрических координатах:

Роль времени теперь играет координата $$, а условие $$ и $$ реализует аналоговую модель расширяющейся вселенной. Точка $$ соответствует моменту Большого взрыва. Действительно, судя по полученной световой картинке, мировые линии частиц в самом деле расходятся в пространстве с течением времени (по мере удаления от $$).

В статье Смолянинова и Хунг также разбирается вопрос о существовании замкнутых времениподобных кривых. Существование замкнутых времениподобных кривых позволяет путешествия во времени со всеми связанными с ними парадоксами. На метаматериале они бы проявились как световые петли — это достаточно очевидно. Однако, в силу разных причин их реализовать не удалось, и, как заключают авторы, скорее всего не удастся. Увы.

Общая теория относительности для инженеров-электриков

Аналогия между электромагнитными полями в метаматериалах и космологией работает в обе стороны. В самом деле, для дизайна метаматериала выполняющего функцию, например, "шапки-невидимки", нужно использовать аппарат общей теории относительности (ОТО). Суть уравнений Эйнштейна ОТО можно сформулировать таким образом: пространство-время указывает материи как ей двигаться, а материя указывает пространству-времени как ему искривляться. Решить уравнение Эйнштейна — значит найти вид метрического тензора пространства-времени, т.е. определить его кривизну исходя из распределения материи.

Шапка-невидимка, скрывающая помещенный внутрь объект, должна так искривлять/преломлять лучи света, чтобы они обходили объект. Искривление световых лучей эквивалентно искривлению пространства-времени, а распределение материи эквивалентно распределению диэлектрической проницаемости (и связанному с ней индексу преломления) в метаматериале. Подробнее с примерами взаимосвязь ОТО и разработки метаматериалов разобрана в статье Ульфа Леонхардта и Томаса Филбина General relativity in electrical engineering.

Также по этой теме:

1. Novello M., Visser M., Volovik G. E. Artificial black holes. – World Scientific, 2002. (особенно глава 3: Slow light)
2. Ralf Schutzhold. Recreating Fundamental Effects in the Laboratory?