Валим всё в одну кучу, как алгебраисты

Что получится, если сложить все-все-все числа друг с другом?

Ребятам, как известно, нравится всё самое‑самое. Чтобы дойти до самой границы изведанного, они смешивают все краски, что есть в доступе, жмут все клавиши разом на музыкальных инструментах. В нашем кружке математики, мы можем позволить себе поразмыслить над любым вопросом, и только от нас зависит будут эти размышления иметь смысл или нет.

Что могут значить слова «сложить» и «все»?

Простейшей математической структурой, в которой эти вопросы имеют смысл можно считать магму: множество с некоторой операцией, позволяющей из любых двух элементов получить третий элемент этого же множества. Слово магма восходит к греческому языку, в котором обозначает тесто, так что бинарную операцию можно рассматривать, как склеивание двух кусков теста, в результате которого вновь получается кусок теста. Математическая магма это настолько свободная структура, что какого‑то внятного ответа на наш вопрос получить не выйдет.

Чуть больше осмысленности можно добиться от магмы, в которой группировка элементов не влияет на результат. Это свойство называется ассоциативностью, и оно позволяет избежать скобок, а магма ассоциативной операцией зовётся полугруппой. Ярким примером полугруппу могут быть строки с конкатенацией. Результатом склеивания всех на свете строк некоторого конечного алфавита будет бесконечное множество всевозможных бесконечных строк. Так себе результат, конечно. Впрочем, если среди символов будут значиться пробелы, символ переноса строки и некоторые спецсимволы, то в это множество войдут все мыслимые программы на Haskell, тексты литературных произведений, ну и куча белиберды, конечно же. А вот если ограничиться только десятью цифрами, то множество всех результатов конкатенации будут представлять множество вещественных чисел от 0 до 1. Действительно, к любой бесконечной цепочке цифр можно приписать слева "0.", и интерпретировать полученную строку, как десятичную дробь. Даже пары символов хватит на то, чтобы каждому числу на интервале поставить в соответствие единственную строку в виде двоичной дроби.

Что‑то ещё более содержательное и при этом универсальное, можно получить, рассматривая группы: множества с обратимой ассоциативной бинарной операцией. От полугруппы их отличает возможность «отменить» склеивание. Группы образуют перестановки, геометрические преобразования (повороты, отражения, сдвиги и пр.), числа с операциями сложения и умножения в кольцах и полях и многие другие полезные объекты. Так что, если мы узнаем ответ на вопрос: «А что будет если сложить всё в одну кучу?» для групп, то это даст нам ключ практически ко всем его осмысленным вариантам.

Обратимость групповой операции приводит к тому, что в группах для каждого элемента отыщется обратный (противоположный) элемент, такой, что они взаимно уничтожают друг друга, как и при сложении или и при умножении. Под «уничтожением» здесь понимается, что результатом получается нейтральный элемент — не изменяющий результата в групповой операции. Так что сваливая все элементы группы в одну кучу, мы будем наблюдать, что некоторые пары элементов с пшиком и шипением взаимно уничтожают друг друга и исчезают, не попадая в итоговый винегрет.

Бесконечные группы

Как ни странно, если группа бесконечная, на наш вопрос ответить проще всего, потому что точный математический ответ звучит так: «А фиг его знает! »

Если начать честно комбинировать все без исключения элементы бесконечной группы, то этот процесс не закончится никогда и никакого внятного ответа мы не дождёмся. Вернее, мы вновь, как и в случае со строками можем получить всё, что угодно. Но процесс становится более любопытным.

Например, работая в группе целых чисел, можно, поступить хитро и складывать числа парами взаимно противоположных элементов:

и так далее, на каждом шаге получая ноль. Таким образом, и в «сумме» тоже получится ноль. Но «ответ» сильно зависит от конкретного выбранного нами способа группировки. Например, такая «сумма»

тоже содержит все элементы, причём, в том же порядке, что и предыдущая, но никакого определённого значения не принимает. Это нарушает основное свойство групповой операции: ассоциативность, а значит предпринимаемое нами действие для группы некорректно.

В конце концов, в качестве «суммы всех целых» чисел можно получить и любое конечное значение. Хотите, единицу:

За исключением первого, все выражения в квадратных скобках равны нулю, а поскольку ряд никогда не закончится, то и нули никогда не переведутся. Ничто не мешает получить и двойку:

В общем, мы имеем дело с настоящей неопределённостью. По этой причине я пишу слова «сумма» и «ответ» в кавычках: для бесконечного ряда целых чисел они не определены.

Может быть, можно говорить о множестве результатов, как в случае со строками? Но ещё раз повторю, для сложения чисел должен выполняться сочетательный закон (ассоциативность), то есть, корректно определённая сумма не должна зависеть от группировки слагаемых. При попытке сложить все целые числа, группировка влияет на результат, а значит, строго говоря, мы имеем дело не с суммой, то есть выходим за пределы группы.

Пара слов о бесконечности

А почему нельзя сказать, что бесконечная сумма единиц, появившаяся в одном из примеров, равна бесконечности ()? Дело в том, что значение нельзя сделать полноценным элементом группы. Для любого элемента в группе должен существовать противоположный элемент, а не нарушив всё того же сочетательного закона, ввести элемент не получится:

Так что вслед за Курантом стоит повторить:

Бесконечность — это не объект, а свойство какого-то процесса никогда не закачиваться.

Если же математики и вводят формальную бесконечную (идеальную) точку или прямую (например, в проективной геометрии или в теории функций комплексной переменной), то работают с ней очень аккуратно, используя не как число, а как способ изменить топологию пространства, построенного на базе числового поля и, так или иначе, «закольцевать» его, и давая возможность уйдя «в бесконечость», вернуться с другой «стороны» сохраняя непрерывность пространства.

Конечные группы

Итак, бесконечное множество чисел складывать смысла немного, а какой результат можно ожидать, если сложить (скомбинировать) все элементы в конечной алгебраической структуре? Этому вопросу посвящён ряд серьёзных работ, ответ тут нетривиален и существенно зависит от внутреннего «устройства» группы.

Конечные группы в контексте нашей задачи делятся на два класса: абелевы и неабелевы.

Абелевы группы

Если в группе наряду с сочетательным законом выполняется переместительный, то такая группа называется коммутативной или абелевой. Для конечных абелевых групп сумма всех элементов выражается достаточно просто: она равна

• ненулевому элементу такому что если такой элемент в группе единственный, либо

• (нейтральному элементу) в противном случае.

Элементы группы, которые противоположны сами себе, называются элементами второго порядка.

Для доказательства рассмотрим три случая.

1) Элементов второго порядка нет. В этом случае все элементы, кроме нуля, разбиваются на пары противоположных друг другу элементов и взаимно уничтожаются. С помощью коммутативности мы всегда сможем в общей сумме поставить противоположные элементы рядом друг с другом.

Пример. Сумма всех чисел в кольце вычетов равна

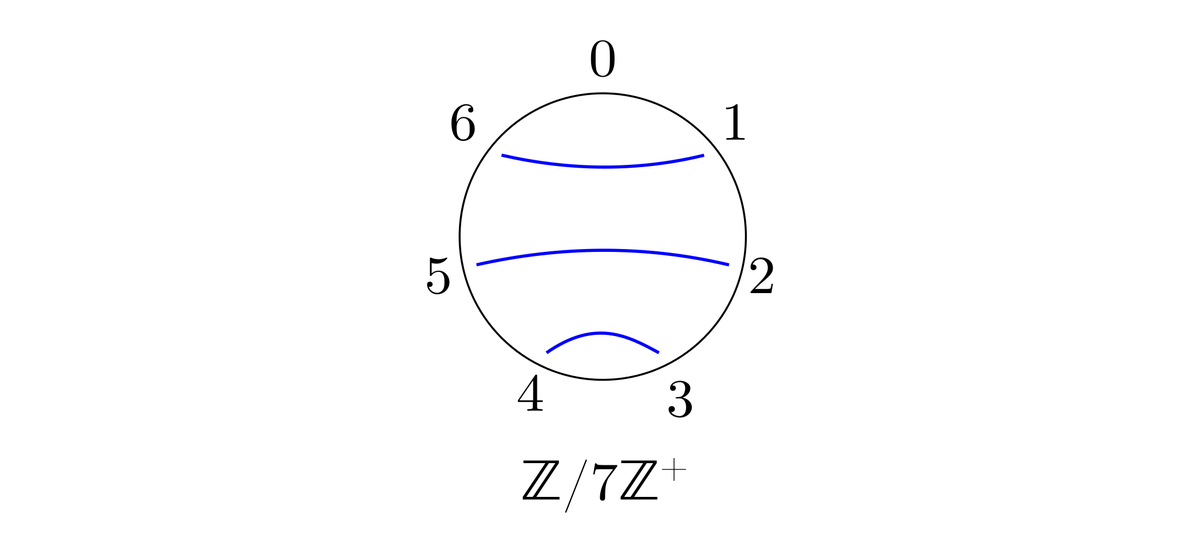
Попытки смухлевать, также как мы это делали с бесконечными группами, здесь не пройдут, поскольку они были основаны на смещении произвольных частичных сумм «в бесконечность». Для конечных сумм эти «задолженности», рано или поздно, придётся компенсировать.

2) Элемент второго порядка существует и он единственный, тогда в общую сумму такой элемент войдёт лишь один раз, тогда как все остальные сложатся со своими противоположными парами и превратятся в ноль.

Примеры. Сумма всех чисел в кольце вычетов В этом кольце , а значит, — это элемент второго порядка (по сложению). Такой элемент в этом кольце единственный и в сумме все элементы в дают .

Ещё одним примером такой группы может быть мультипликативная группа в кольце в которой и есть элемент второго порядка: . Произведение всех элементов этой группы равно .

Любопытное замечание: если в абелевой группе с единственным элементом второго порядка сложить все элементы друг с другом дважды, то получится ноль.

3) Элементов второго порядка больше одного. В любой абелевой группе количество элементов, обратных самим себе, всегда на единицу меньше некоторой степени двойки: Это связано с тем, что любая комбинация таких элементов тоже является элементом обратным самому себе.

Предположим, что в группе есть два различных элемента второго порядка  и . Поскольку . Элемент не может быть равен ни  ни  и он, как видим, тоже имеет второй порядок, таким образом, где есть два таких элемента, должен быть и третий. Вместе с нулем они образуют собственную группу . Все её элементы можно представить, как пары , элементы этих пар принадлежат простейшей нетривиальной группе , содержащей всего два элемента: . При сложении пар компоненты складываются, как векторы, причём . Такую конструкцию из пар называют прямым произведением групп. В нашем случае, это .

В общем случае, элементы второго порядка всегда образуют группу , которая имеет структуру, сходную с векторным пространством размерности с компонентами из

Зачем мы так всё усложнили? А чтобы увидеть, что сумма всех таких векторов равна нулю, потому что каждый компонент равен единице ровно в половине из них, и если количество векторов больше двух, то число единиц при суммировании будет чётным.

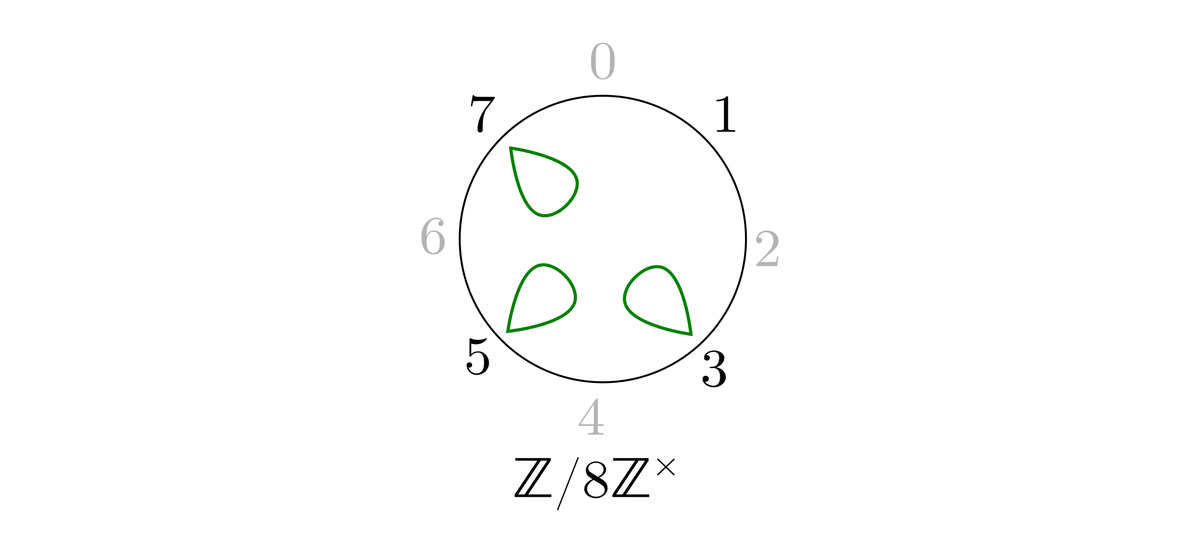
Пример. Мультипликативная группа в кольце , состоящая из элементов В ней три элемента второго порядка: и произведение всех элементов ожидаемо равно .

Теорема Уилсона

В числовых кольцах и полях сложение должно образовывать абелеву группу, а во многих из них (кольца вычетов, кольца многочленов, комплексные и гауссовы числа) умножение тоже коммутативно, так что полученное нами знание об абелевых группах позволяет сказать, что если сложить все числа вместе, то получится, либо ноль, либо единственный элемент второго порядка, если такой существует. Это же относится и к умножению, но в этом случае нужно заменить ноль на единицу.

В этой связи обычно вспоминают теорему Уилсона, которая утверждает, что для простого числа факториал числа  сравним с по модулю :

Доказательство. Кольца вычетов по простому модулю p представляют собой поля, в которых умножение образует группу с элементами . В этой группе есть единственный элемент второго порядка:  Так что эта теорема следует непосредственно из доказанного нами обобщённого результата для абелевых групп.

Если последовательно строить кольцо целых чисел, рассматривая его как предел кольца вычетов по модулю, стремящемуся к бесконечности, то относительно сложения мы получим абелеву группу для которой, как мы знаем, есть два варианта: ноль или элемент второго порядка. Но поскольку бесконечный элемент корректно ввести в группу нельзя, то с формальной алгебраической точки зрения, сумма всех целых чисел должна быть равна нулю, как, собственно, и произведение.

Неабелевы группы

Для групп, в которых переместительный закон (коммутативность) действует не всегда, дела обстоят несколько сложнее.

Имея группу , можно выделить некую особую нормальную подгруппу , такую, что где  — абелева. Минимальная подгруппа такого рода называется коммутантом группы , и в известном смысле, отражает степень её неабелевости. Любой элемент коммутанта можно выразить в виде произведения , где и какие‑то элементы группы (неабелеву групповую операцию принято называть и обозначать умножением). В 1982 году была сформулирована и доказана теорема Денеса‑Германна, о том, что комбинируя все элементы произвольной группы , можно получить либо какой‑то из элементов коммутанта , либо элемент коммутанта, умноженный на элемент второго порядка.

Примеры. Рассмотрим группу перестановок из трёх элементов , самую маленькую неабалеву группу. В этой группе есть три элемента второго порядка: транспозиции и две циклических перестановки и , ну и конечно, нейтральный элемент . Коммутантом группы является подгруппа циклических перестановок. И в каком бы порядке мы не перемножали все шесть перестановок третьего порядка (а таких вариантов ), будет получаться одна из трёх транспозиций: , или , которые можно получить, умножив циклическую перестановку на какой‑либо из элементов второго порядка.

Чему равен факториал отрицательного числа?

Если честно следуя определению, попытаться посчитать факториал от отрицательного числа, то ничего не получится: убывающий ряд целых чисел никогда не закончится и ни к какому результату мы не придём. Однако в конечных арифметиках результат получится вполне определённым.

В предыдущей части мы упомянули теорему Уилсона которая говорит чему равен факториал наибольшего числа в модулярной арифметике с простым модулем:

Но эта теорема ничего не говорит нам о том, как выглядят прочие факториалы, если вычислять их в конечном поле . Об этом я и предлагаю поразмыслить.

Напомню, что полем называется числовая система, в которой определены операции сложения и умножения с обычными законами: сочетательным, распределительным и переместительным для сложения. У каждого ненулевого элемента  в поле есть противоположный и обратный . В полях вычетов (кольцах с простыми модулями) для умножения переместительный закон тоже выполняется. Арифметика остатков от целочисленного деления на число  будет полем, если  — простое число.

В поле число  , так что утверждение теоремы Уилсона в нём можно записать так:

Выглядит, согласитесь, достаточно просто. А что можно сказать о величине в конечном поле? Это легко вычислить:

Тоже неплохое значение, причем, в отличие от , оно выглядит одинаково во всех полях вычетов, не зависимо от их модуля!

Такое простое значение позволяет легко вычислить

Конкретное значение числа, противоположного обратному двойке, зависит от модуля, так что имеет смысл оставить этот ответ в такой форме. Сделаем ещё пару шагов назад:

Теперь можно сказать, что мы нащупали общую картину:

Таким образом, получается обобщение теоремы Уилсона для конечных полей вычетов. Как видно, факториалы в поле вычетов ведут себя достаточно симметрично:

Число не входит в мультипликативную группу поля, поэтому мы искусственно положили Это, во-первых, хорошо вписывается в найденную нами схему:

а во‑вторых, соответствует духу алгебры: «пустое» произведение (без множителей) должно, всё‑таки, быть произведением, то есть, элементом мультипликативной группы, а поскольку оно незримо входит в любое произведение и не меняет его, то оно должно быть равно нейтральному элементу этой группы — единице.

А если числа не целые?

Дополнение для тех, кто знаком с гамма-функцией и элементами комплексного анализа. Как известно, вещественным аналогом факториала является гамма-функция, при этом для целых

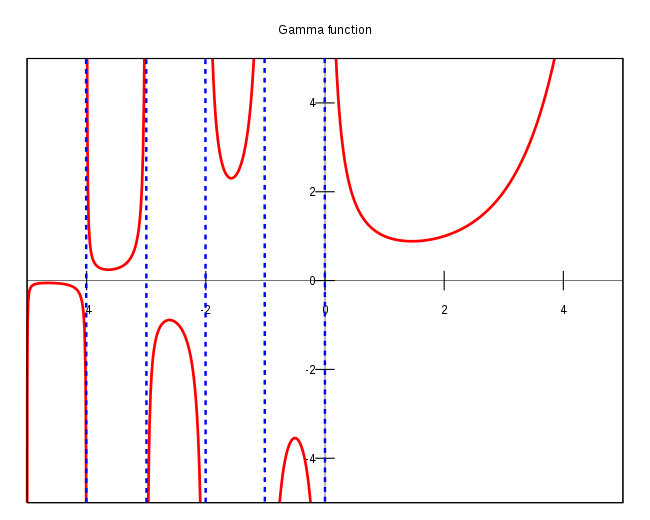
В целых отрицательных точках гамма функция терпит разрыв. Так что и наивное определение факториала и более изощрённое не дают определённого ответа на вопрос чему равен, например, факториал от в целых числах?

При этом в окрестности точки гамма-функция ведет себя, как гипербола:

Коэффициент называется вычетом функции, и вычисляется методами теории функций комплексной переменной. Для гамма-функции он в точности совпадает с полученным нами выражением для факториала в конечном поле. Действительно, если формально записать, что подставить в выражение для вычета, и привести знаки, то получится:

Вот так красиво согласуются между собой алгебра, комплексный анализ и теория чисел.