Визуальная теория информации (часть 1)

Перевод интересного лонгрида посвященного визуализации концепций из теории информации. В первой части мы посмотрим как отобразить графически вероятностные распределения, их взаимодействие и условные вероятности. Далее разберемся с кодами фиксированной и переменной длины, посмотрим как строится оптимальный код и почему он такой. В качестве дополнения визуально разбирается статистический парадокс Симпсона.

Теория информации дает нам точный язык для описания многих вещей. Сколько во мне неопределенности? Как много знание ответа на вопрос А говорит мне об ответе на вопрос Б? Насколько похож один набор убеждений на другой? У меня были неформальные версии этих идей, когда я был маленьким ребенком, но теория информации кристаллизует их в точные, сильные идеи. Эти идеи имеют огромное разнообразие применений, от сжатия данных до квантовой физики, машинного обучения и обширных областей между ними.

К сожалению, теория информации может казаться пугающей. Я не думаю, что есть какая-то причина для этого. Фактически, многие ключевые идеи могут быть объяснены визуально!

Визуализация вероятностных распределений

Прежде чем мы углубимся в теорию информации, давайте подумаем о том, как можно визуализировать простые вероятностные распределения. Они нам понадобятся позже, кроме того эти приемы для визуализации вероятностей полезны сами по себе!

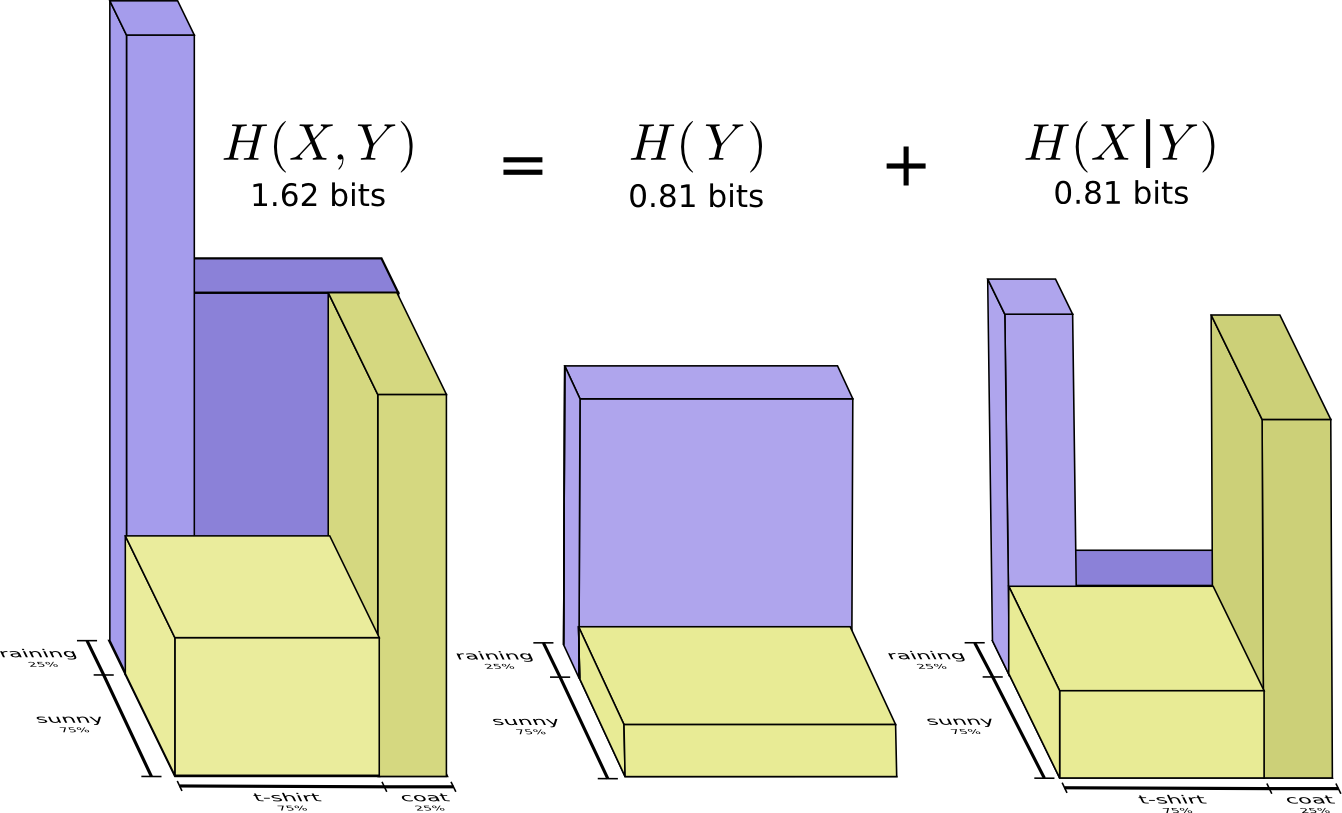
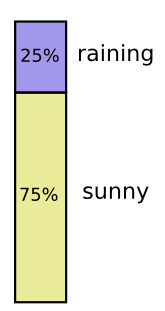
Я в Калифорнии. Иногда идет дождь, но в основном солнце! Скажем, в 75% случаев солнечно. Это легко изобразить на рисунке:


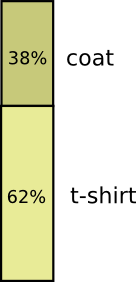
Большинство дней я ношу футболку, но иногда я ношу плащ. Допустим, я ношу плащ 38% времени. Это тоже легко изобразить.


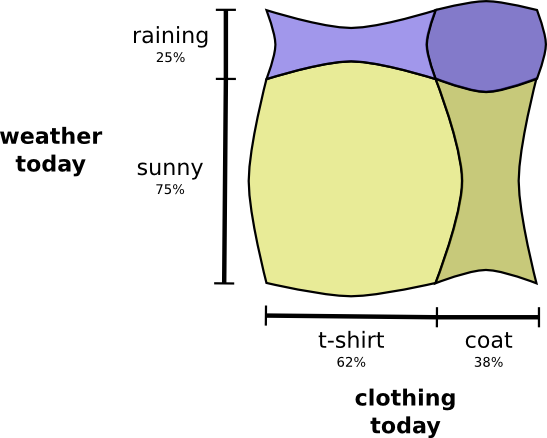
Что делать, если я хочу визуализировать оба факта одновременно? Это просто, если они не взаимодействуют — т.е. независимы. Например, если то: что я ношу сегодня футболку или плащ, не зависит от погоды на следующей неделе. Мы можем изобразить это, используя одну ось для одной переменной и одну для другой:



Обратите внимание на прямые вертикальные и горизонтальные линии, проходящие насквозь. Вот как выглядит независимость! Вероятность того, что я ношу плащ, не изменится в связи с тем, что через неделю будет дождь. Другими словами, вероятность того, что я надену плащ и что на следующей неделе пойдет дождь, равна вероятности того, что я надену плащ, умноженной на вероятность того, что пойдет дождь. Они не взаимодействуют.

Когда переменные взаимодействуют, вероятность может увеличивать для одних пар переменных и уменьшаться для других. Существует большая вероятность того, что я ношу плащ и идет дождь, потому что переменные коррелируют, они делают друг друга более вероятными. Более вероятно, что я ношу плащ в день, когда идет дождь, чем вероятность того, что я ношу плащ в один день, а дождь идет в другой случайный день.

Визуально это выглядит так, как будто некоторые из квадратов разбухают с дополнительной вероятностью, а другие квадраты сужаются, потому что пара событий вряд ли произойдет одновременно:



Но хотя это выглядит круто, это не очень полезно для понимания происходящего.

Вместо этого давайте сосредоточимся на такой переменной как погода. Мы знаем вероятности солнечной и дождливой погоды. В обоих случаях мы можем рассмотреть условные вероятности. Какова вероятность того, что я надену футболку, если солнечно? Какова вероятность того, что я надену плащ, если идет дождь?


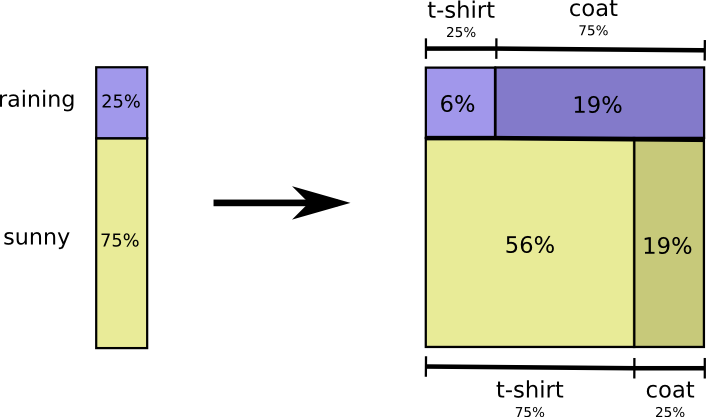
С вероятностью 25% идет дождь. Если идет дождь, с вероятностью 75% я надену плащ. Таким образом, вероятность того, что идет дождь, и я ношу плащ, равна 25% от 75%, что составляет приблизительно 19%. Вероятность того, что идет дождь, и я ношу плащ, — это вероятность того, что идет дождь, умноженная на вероятность того, что я буду носить плащ, если идет дождь. Мы записываем это так:

$$

Это пример одного из самых фундаментальных тождеств теории вероятностей:

$$

Мы факторизуем распределение, разбивая его на произведение из двух частей. Сначала мы смотрим вероятность того, что одна переменная — погода, примет определенное значение. Затем мы смотрим на вероятность того, что другая переменная — моя одежда, примет значение, обусловленное первой переменной.

С какой переменной начинать не имеет значения. Мы могли бы начать с моей одежды, а затем посмотреть на погоду, обусловленную этим. Это может показаться менее интуитивным, потому что мы понимаем, что есть причинно-следственная связь погоды, влияющей на то, что я ношу, а не наоборот… но это все равно работает!

Давайте рассмотрим пример. Если мы выберем случайный день, с вероятностью 38% я буду носить плащ. Если мы знаем, что я в плаще, насколько вероятно, что идет дождь? Я скорее надену плащ в дождь, чем на солнце, но дождь в Калифорнии редкость, и получается, что с вероятностью 50% идет дождь. Итак, вероятность того, что идет дождь, и я ношу плащ, — это вероятность того, что я буду носить плащ (38%), умноженная на вероятность того, что будет дождь, если я буду носить плащ (50%), что составляет примерно 19%.

$$

Это дает нам второй способ визуализации того же распределения вероятностей.


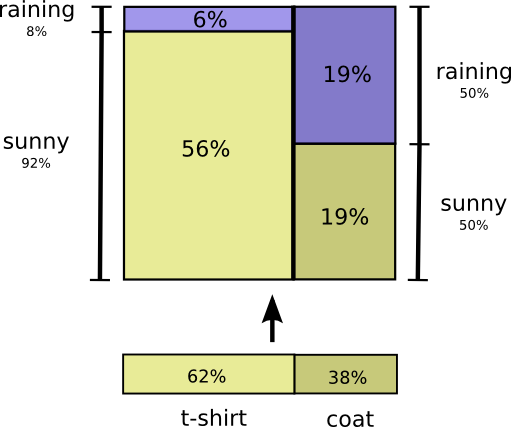
Обратите внимание, что значения меток имеют несколько иное значение, чем на предыдущей диаграмме: футболка и плащ теперь являются предельными вероятностями, вероятность того, что я надену эту одежду без учета погоды. С другой стороны, теперь есть две дождевые и солнечные метки, потому что вероятности их зависят от того, что я буду носить футболку или плащ.

(Возможно, вы слышали о теореме Байеса. Вы можете представлять ее как способ перехода между этими двумя различными способами отображения распределения вероятностей!)

Вставка: Парадокс Симпсона

Действительно ли полезны эти приемы визуализации вероятностных распределений? Я думаю, что да! Чуть дальше мы используем их для визуализации теории информации, а пока используем их для изучения парадокса Симпсона. Парадокс Симпсона — крайне неинтуитивная статистическая ситуация. Ее трудно понять на интуитивном уровне. Майкл Нильсен написал прекрасное эссе Reinventing Explanation, в котором парадокс объясняется разными способами. Я хочу попробовать сделать это самостоятельно, используя приемы, которые мы разработали в предыдущем разделе.

Тестируются два метода лечения камней в почках. Половина пациентов получают лечение А, в то время как другая половина получает лечение Б. Пациенты, получавшие лечение Б, выздоравливали с большей вероятностью, чем те, кто получал лечение А.


Однако пациенты с мелкими почечными камнями имели большую вероятность выздоровления, если они получали лечение А. Пациенты с крупными почечными камнями в почках также имели больше шансов выздороветь, если они получали лечение А! Как такое может быть?

Суть проблемы в том, что исследование не было должным образом рандомизировано. Среди пациентов получавших лечение A, было больше тех, у кого крупные камни в почках, а среди пациентов получавших лечение B было больше с мелкими камнями в почках.


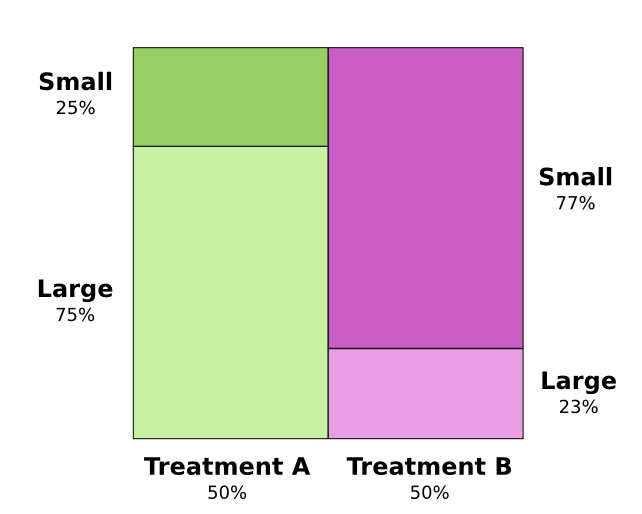
Как выясняется, пациенты с небольшими камнями в почках гораздо чаще выздоравливают в целом.

Чтобы лучше это понять, мы можем объединить две предыдущие диаграммы. Результатом является трехмерная диаграмма с коэффициентом выздоровления, разделенным на мелкие и крупные почечные камни.


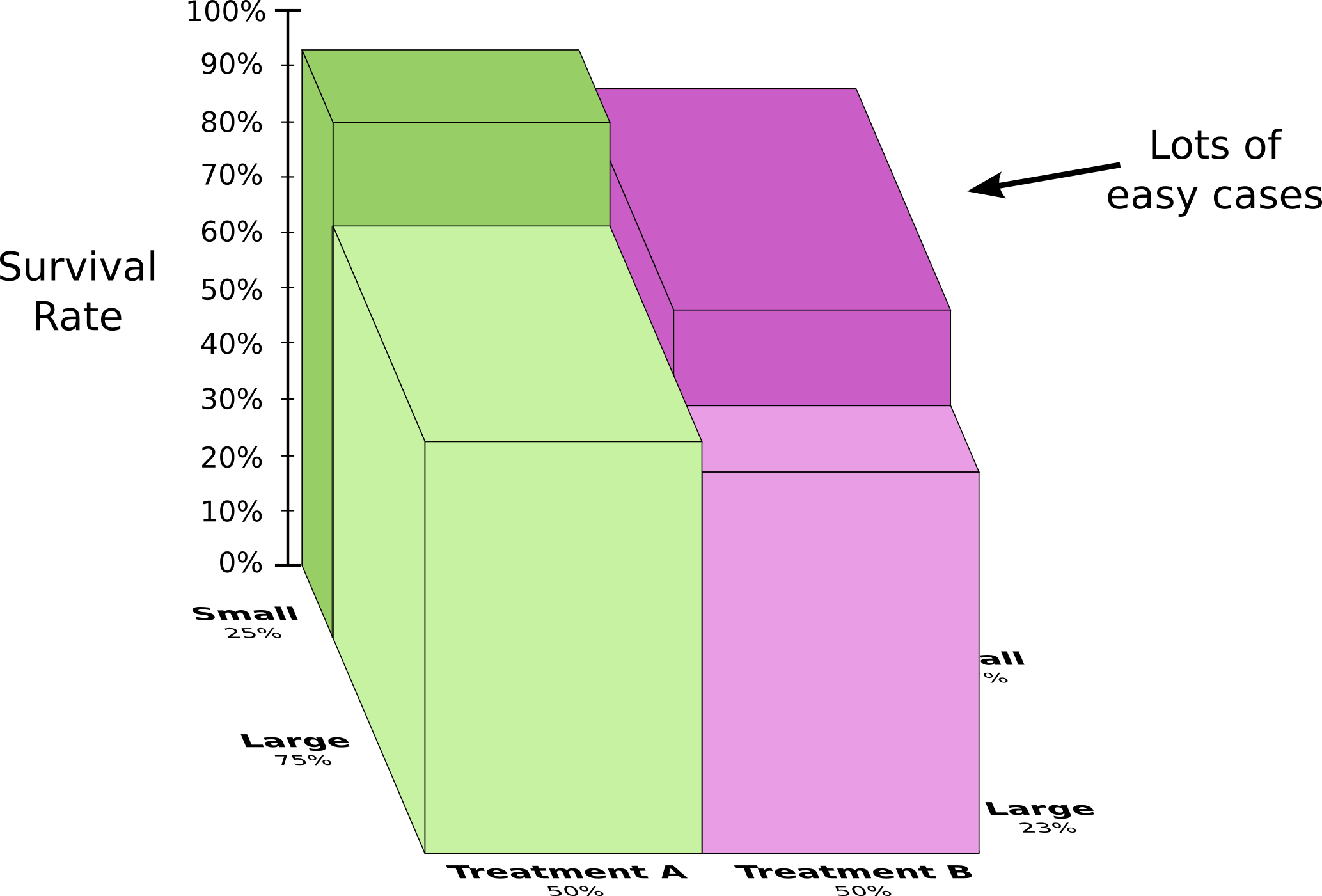
Теперь мы видим, что как в случае с маленькими камнями, так и большими лечение A превосходит лечение B. Лечение B выглядело лучше только потому, что пациенты, к которым оно применялось, имели в общем больше шансов выздороветь!

Коды

Теперь, когда у нас есть способы визуализации вероятности, мы можем погрузиться в теорию информации.

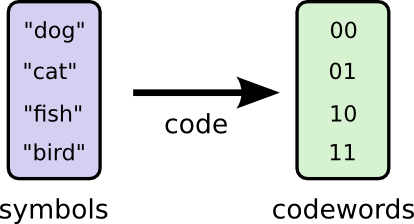
Позвольте мне рассказать вам о моем воображаемом друге, Бобе. Боб очень любит животных. Он постоянно говорит о животных. Фактически он говорит только четыре слова: «dog», «cat», «fish» и «bird».

Пару недель назад, несмотря на то, что Боб был плодом моего воображения, он переехал в Австралию. Кроме того, он решил, что хочет общаться только в двоичном формате. Все мои (воображаемые) сообщения от Боба выглядят так:


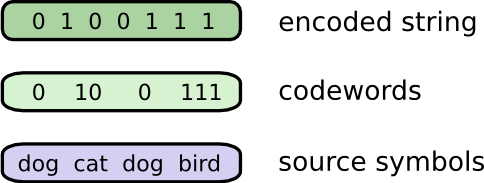
Чтобы общаться, Боб и я должны создать систему кодирования — способ отображения слов в последовательности битов.


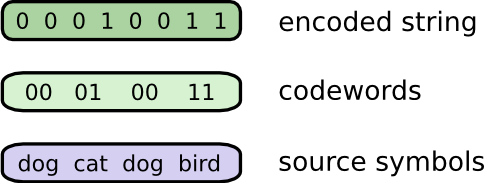
Чтобы отправить сообщение, Боб заменяет каждый символ (слово) соответствующим кодовым словом, затем объединяет их вместе, чтобы сформировать кодированную строку.

Коды переменной длины

К сожалению, услуги связи в воображаемой Австралии стоят дорого. Я должен платить 5 долларов за бит каждого сообщения, которое я получаю от Боба. Я уже говорил, что Боб любит много говорить? Чтобы не обанкротиться, мы с Бобом решили выяснить, можно ли каким-то образом сократить среднюю длину сообщения.

Оказывается, Боб не произносит все слова одинаково часто. Боб очень любит собак. Он говорит о собаках все время. Иногда он говорит о других животных — особенно о кошке, за которой его собака любит гоняться — но в основном он говорит о собаках. Вот график частоты его слов:


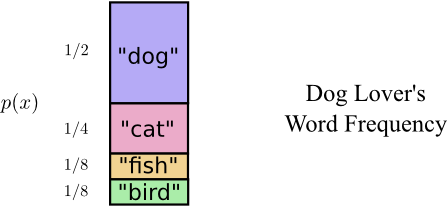
Это обнадеживает. Наш старый код использует кодовые слова длиной 2 бита, независимо от того, насколько часто они используются.

Есть хороший способ визуализировать это. На следующей диаграмме мы используем вертикальную ось для визуализации вероятности каждого слова $$ и горизонтальную ось для визуализации длины соответствующего кодового слова $$. Обратите внимание, что полученная площадь — это средняя длина отправляемого нами кодового слова — в данном случае 2 бита.


Мы можем быть умнее и сделать код переменной длины, где кодовые слова для распространенных слов сделаны более короткими. Проблема в том, что существует конкуренция между кодовыми словами — делая одни короче, мы вынуждены делать другие длиннее. Чтобы минимизировать длину сообщения, в идеале нам хотелось бы, чтобы все кодовые слова были короткими, но самыми короткими должны быть широко используемые. Таким образом, полученный код содержит кодовые слова меньшей длины для распространенных слов (например, «dog») и кодовые слова большей длины для редких слов (например, «bird»).


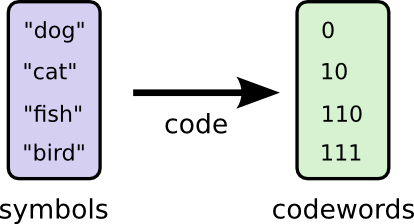
Давайте вновь визуализируем это. Обратите внимание, что самые распространенные кодовые слова стали короче, а самые редкие — длиннее. В результате мы получили, меньшую площадь. Это соответствует меньшей ожидаемой длине кодового слова. В среднем длина кодового слова теперь составляет 1,75 бита!



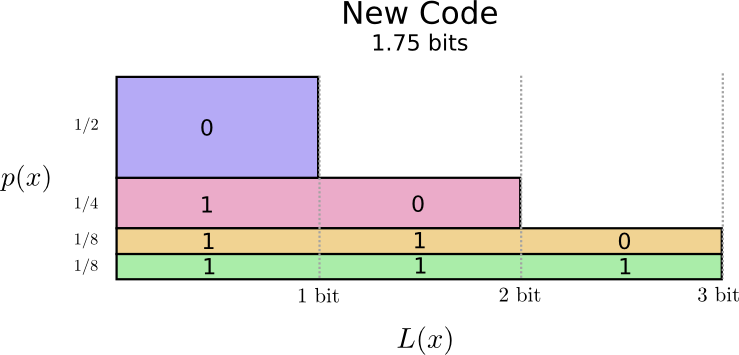
(Вы можете поинтересоваться: почему бы не использовать 1 отдельно в качестве кодового слова? К сожалению, это вызовет неоднозначность, при декодировании закодированных строки. Мы поговорим об этом подробнее чуть позже.)

Оказывается, этот код является наилучшим из возможных. Не существует кода, для этого распределения который дал бы нам среднюю длину кодового слова менее 1,75 бит.

Существует фундаментальный предел. Передача того, какое слово было сказано, какое событие из этого распределения произошло, требует от нас передачи в среднем не менее 1,75 бит. Каким бы умным ни был наш код, невозможно добиться того, чтобы средняя длина сообщения была меньше. Мы называем этот фундаментальный предел энтропией распределения — далее мы обсудим его более подробно.



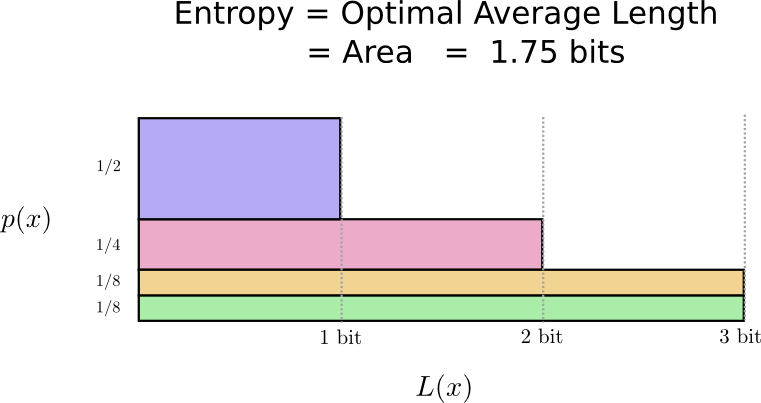
Если мы хотим понять этот предел, нам нужно понять компромисс между тем чтобы делать одни кодовые слова короткими, а другие длинными. Как только мы разберемся с этим, мы сможем понять как выглядят наилучшие возможные системы кодирования.

Пространство кодовых слов

Существует два кодовых слова длиной 1 бит: 0 и 1. Существует четыре кодовых слова длиной 2 бита: 00, 01, 10 и 11. Каждый добавляемый вами бит удваивает количество возможных кодовых слов.


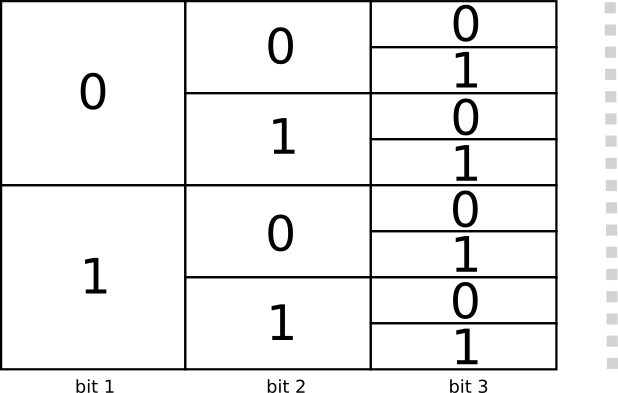
Мы интересуемся кодами переменной длины, где некоторые кодовые слова длиннее других. У нас могут быть простые ситуации, когда у нас есть восемь кодовых слов длиной 3 бита. Могут быть и более сложные смеси, например, два кодовых слова длины 2 и четыре кодовых слова длины 3. Что решает, сколько кодовых слов разной длины мы можем иметь?

Вспомните, что Боб превращает свои сообщения в зашифрованные строки, заменяя каждое слово его кодом и объединяя их.


Есть тонкий вопрос, с которым нужно быть осторожным при создании кодов переменной длины. Как мы разделим закодированную строку обратно на кодовые слова? Когда у всех кодовых слов одинаковая длина, это легко — просто разделите строку на куски этой длины. Но поскольку существуют кодовые слова различной длины, нам нужно обращать внимание на содержимое.

Мы хотим, чтобы наш код был однозначно декодируемым. И не хотим, чтобы он был двусмысленным при определении того, какие кодовые слова составляют закодированную строку. Если бы у нас был специальный символ «конец кодового слова», это было бы просто. Но у нас нет такого — мы посылаем только 0 и 1. Нам нужно иметь возможность взглянуть на последовательность кодовых слов и определять, где заканчивается каждое из них.

Очень просто сделать коды, которые не поддаются однозначной расшифровке. Например, представьте, что 0 и 01 оба кодовые слова. Тогда неясно, каким является первое кодовое слово строки 0100111 — им может быть либо то, либо другое! Свойство, которое нам нужно, заключается в том, что если мы видим конкретное кодовое слово, оно не должно включаться в другое, более длинное кодовое слово. По другому говоря, ни одно кодовое слово не должно быть префиксом другого кодового слова. Это называется свойством префикса, а коды, которые ему подчиняются, называются префиксными кодами.

Полезный способ представления этого заключается в том, что каждое кодовое слово требует жертв из пространства возможных кодовых слов. Если мы берем кодовое слово 01, мы теряем возможность использовать любые кодовые слова, префиксом которых он является. Мы больше не можем использовать 010 или 011010110 из-за двусмысленности — они для нас потеряны.


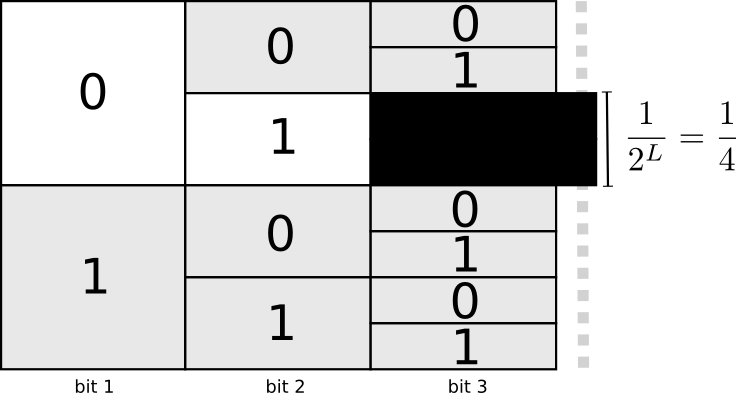
Поскольку четверть всех кодовых слов начинается с 01, мы пожертвовали четвертью всех возможных кодовых слов. Вот цена, которую мы платим в обмен на то, что у нас одно кодовое слово длиной всего 2 бита! В свою очередь, эта жертва означает, что все остальные кодовые слова должны быть немного длиннее. Всегда есть своего рода компромисс между длинами разных кодовых слов. Короткое кодовое слово требует от вас пожертвовать большей частью пространства возможных кодовых слов, что препятствует краткости других кодовых слов. То, что нам нужно выяснить, это как сделать компромисс правильно!

Оптимальное кодирование

Вы можете думать об этом, как об ограниченном бюджете который можно потратить на получение коротких кодовых слов. Мы платим за одно кодовое слово, жертвуя частью возможных кодовых слов.

Стоимость покупки кодового слова длины 0 равна 1 — все возможные кодовые слова — если вы хотите иметь кодовое слово длины 0, у вас не может быть никакого другого кодового слова. Стоимость кодового слова длиной 1, например «0», составляет 1/2, потому что половина возможных кодовых слов начинается с «0». Стоимость кодового слова длиной 2, например «01», составляет 1/4, потому что четверть всех возможных кодовых слов начинается с «01». В общем случае стоимость кодовых слов уменьшается экспоненциально с увеличением длины кодового слова.



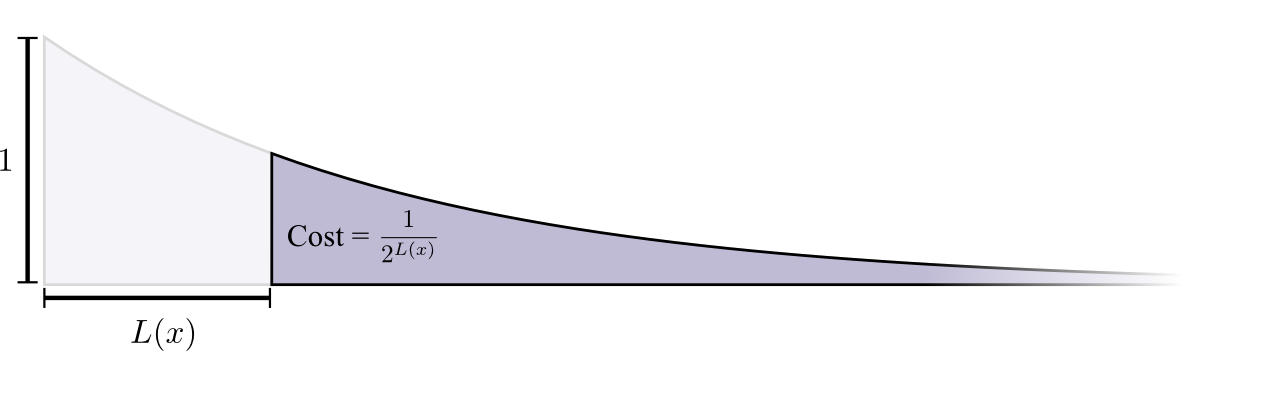
Обратите внимание, что если стоимость уменьшается как (натуральная) экспонента, это и высота, и площадь! (В примере использовалась экспонента с основанием 2 где этот факт неверен, но можно переключиться на натуральную экспоненту, что визуально упрощает доказательство.)

Нам нужны короткие кодовые слова, потому что мы хотим уменьшить средние длины сообщений. Каждое кодовое слово увеличивает среднюю длину сообщения на вероятность этого слова, умноженную на ее длину. Например, если нам нужно отправить кодовое слово длиной 4 бита 50% времени, наша средняя длина сообщения будет на 2 бита больше, чем если бы мы не отправляли это кодовое слово. Мы можем представить это как прямоугольник.


Эти два значения связаны длиной кодового слова. Цена, которую мы платим, определяет длину кодового слова. От длины кодового слова зависит, сколько оно добавляет к средней длине сообщения. Мы можем представить их вместе, вот так.



Короткие кодовые слова уменьшают среднюю длину сообщения, но стоят дорого, в то время как длинные кодовые слова увеличивают среднюю длину сообщения, но стоят дешево.



Как лучше всего использовать наш ограниченный бюджет? Сколько мы должны потратить на кодовое слово для каждого события?

Точно так же, как человек хочет инвестировать больше средств в инструменты, которые регулярно использует, мы хотим тратить больше на часто используемые кодовые слова. Есть один особенно естественный способ сделать это: распределить наш бюджет пропорционально тому, насколько часто происходит событие. Итак, если событие происходит в 50% случаев, мы тратим 50% нашего бюджета на покупку короткого кодового слова для него. Но если событие происходит только 1% времени, мы тратим только 1% нашего бюджета, потому что нас не сильно волнует, длина кодового слова.

Это довольно естественная вещь, но оптимальна ли она? Это так, и я докажу это!

Следующее доказательство наглядно и должно быть понятно, но чтобы разобрать его потребуется работа, и это определенно самая сложная часть этого эссе. Читатели могут смело пропустить ее, приняв факт без доказательства и перейти к следующему разделу.

Давайте посмотрим конкретный пример, где нам нужно сообщить, какое из двух возможных событий произошло. Событие $$ происходит $$ времени, а событие $$ происходит $$ времени. Мы распределяем наш бюджет естественным образом, описанным выше, тратя $$ нашего бюджета на получение короткого кодового слова $$ и $$ на получение короткого кодового слова $$.



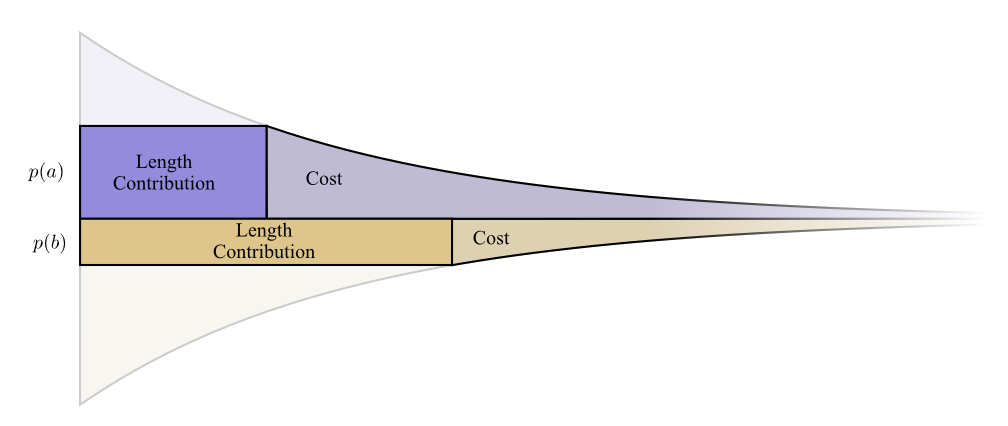
Границы стоимости и длины красиво выстраиваются. Это что-нибудь значит?

Рассмотрим, что произойдет с вкладом стоимости и длины, если мы немного изменим длину кодового слова. Если мы немного увеличим длину кодового слова, то вклад длины сообщения увеличится пропорционально его высоте на границе, а стоимость уменьшится пропорционально его высоте на границе.



Таким образом, стоимость создания более короткого кодового слова составляет $$. Нас не волнует длина каждого кодового слова в равной степени, они интересуют нас пропорционально тому, насколько часто мы их используем. В случае $$ — это $$. Наш выигрыш от того, что мы сделаем кодовое слово немного короче, пропорционален $$.

Интересно, что обе производные одинаковы. Это значит, что у нашего начального бюджета есть интересная особенность: если бы у вас было немного больше средств, было бы одинаково хорошо инвестировать в сокращение любого кодового слова. То, что нас действительно волнует, это соотношение выгоды/затрат — вот что решает, во что нам следует больше инвестировать. В этом случае соотношение $$, что равно единице. Оно не зависит от значения p(a) — оно всегда равно единице. И мы можем применить тот же аргумент к другим событиям. Выгода/стоимость всегда одна, поэтому имеет смысл вкладывать немного больше в любое из событий.



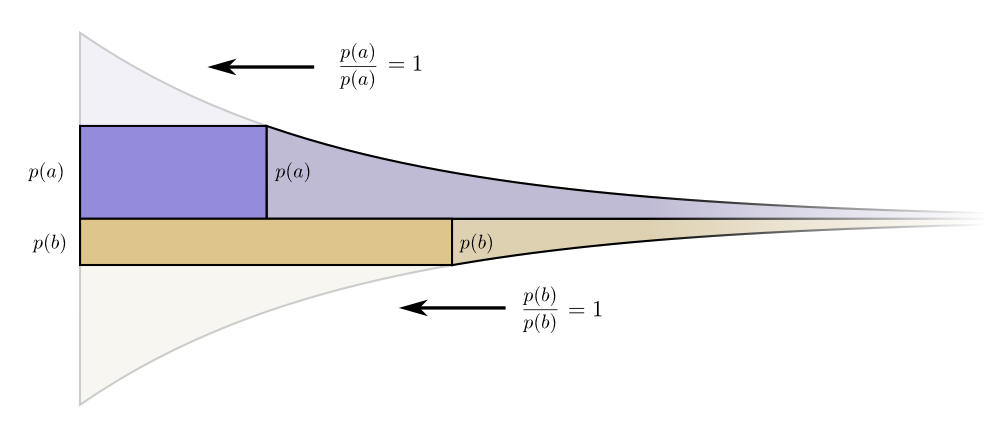
В терминах бесконечно малых, менять бюджет не имеет смысла. Но это не доказательство того, что это лучший бюджет. Для доказательства, мы рассмотрим другой бюджет, где мы тратим немного больше на одно кодовое слово за счет другого. Мы потратим на $$ меньше на $$, и добавим этот $$ событию $$. Это делает кодовое слово для $$ немного короче, а кодовое слово для $$ немного длиннее.

Теперь стоимость покупки более короткого кодового слова для $$ равна $$, а стоимость покупки более короткого кодового слова для $$ равна $$. Но выгода все та же. Это приводит к тому, что соотношение стоимость/выгода для покупки $$ будет $$, которое меньше единицы. С другой стороны, соотношение стоимость/выгода покупки b составляет $$, что больше единицы.



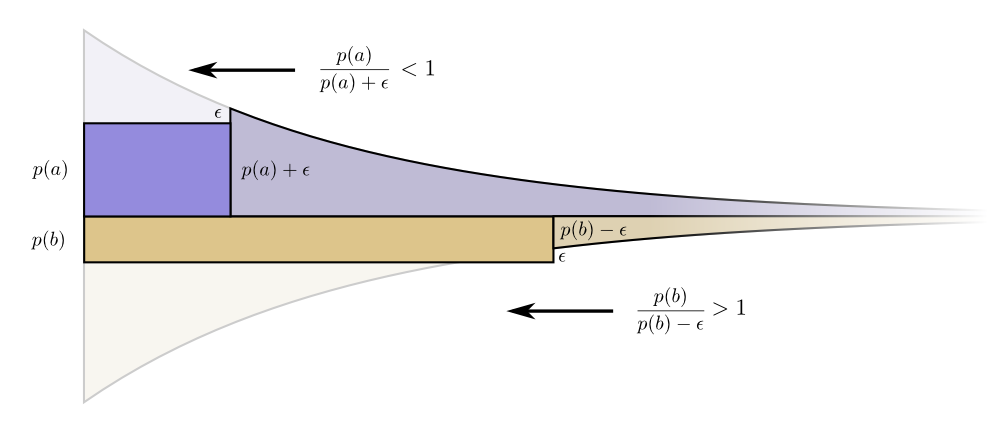
Цены больше не сбалансированы. $$ лучшая сделка, чем $$. Инвесторы кричат: «Купите $$! Продайте $$!» Мы делаем это и возвращаемся к нашему первоначальному бюджетному плану. Все бюджеты можно улучшить путем возвращения к нашему первоначальному плану.

Первоначальный бюджет — инвестирование в каждое кодовое слово пропорционально тому, как часто мы его используем, — было не просто естественным, а оптимальным вариантом. (Наше доказательство работает только для двух кодовых слов, оно легко обобщается на большее количество.)

(Внимательный читатель, возможно, заметил, что в случае оптимального бюджета могут получиться коды, в которых кодовые слова имеют дробную длину. Что это значит? На практике, если вы хотите общаться, посылая одно кодовое слово, вам придется округлить значение. Но как мы увидим позже, есть реальный смысл, в том чтобы посылать дробные кодовые слова, когда мы отправляем их много одновременно!)

P.S. Продолжение будет посвящено энтропии, кросс-энтропии, взаимной информации, дробным битам и прочим интересным штукам.