Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В этой статье мы добавим в наш рейтрейсер поддержку отражения и преломления света. Приятного чтения!
Предыдущая глава
Другим преимуществом трассировки лучей является то, что, расширяя идею распространения лучей, мы можем очень легко имитировать такие эффекты, как отражение и преломление, которые удобны при моделировании стеклянных материалов или зеркальных поверхностей. В статье 1979 года, озаглавленной "Улучшенная модель освещения для затененного дисплея", Тернер Уиттед был первым, кто описал, как расширить алгоритм трассировки лучей Аппеля для более продвинутого рендеринга. Идея Уиттеда расширила модель испускания лучей Аппелем, включив в нее расчеты отражения и преломления.

В оптике отражение и преломление - хорошо известные явления. Хотя последующий урок посвящен отражению и преломлению, мы рассмотрим, что необходимо для их имитации. Мы возьмем пример стеклянного шара, обладающего как преломляющими, так и отражающими свойствами. Пока мы знаем направление луча, пересекающего шар, легко вычислить, что с ним происходит. Как направления отражения, так и преломления основаны на нормали в точке пересечения и направлении входящего луча (первичного луча). Чтобы вычислить направление преломления, нам также необходимо указать показатель преломления материала. Хотя ранее мы говорили, что лучи движутся по прямой линии, мы можем визуализировать преломление как искривление луча. Его направление меняется, когда фотон попадает на объект из другой среды (и, следовательно, с другим показателем преломления). Это явление с точки зрения физики будет более подробно рассмотрена позже. Мы готовы двигаться дальше, если помним, что эти два эффекта зависят от вектора нормали и направления входящего луча, а преломление зависит от показателя преломления материала.
Точно так же мы также должны осознавать тот факт, что объект, подобный стеклянному шару, является отражающим и преломляющим одновременно. Нам нужно вычислить и то, и другое для заданной точки на поверхности, но как нам их смешать? Смешиваем ли мы 50% результата отражения с 50% результата преломления? К сожалению, все гораздо сложнее. Смешение значений зависит от угла между основным лучом (или направлением обзора) и нормалью объекта и показателем преломления. Однако, к счастью для нас, уравнение точно вычисляет, как следует смешивать каждый из них. Это уравнение известно как уравнение Френеля. Чтобы быть кратким, все, что нам нужно знать на данный момент, это то, что он существует и поможет определить значения смешивания.
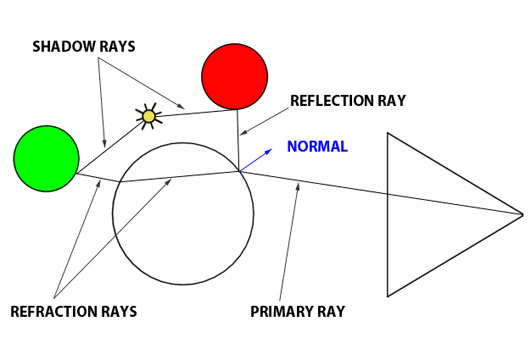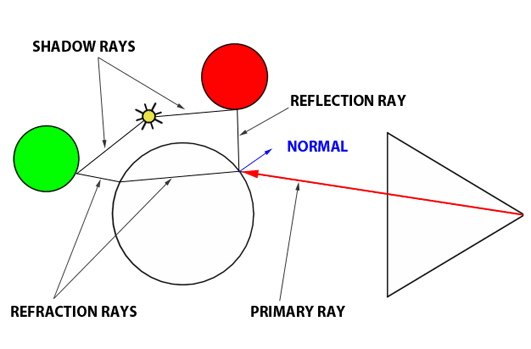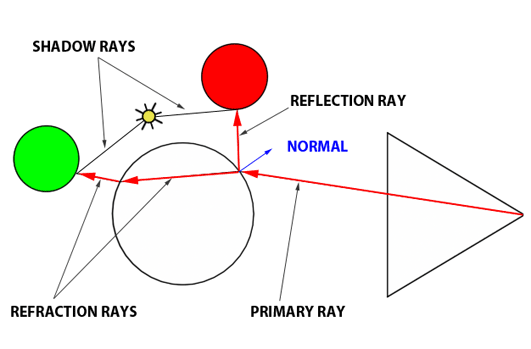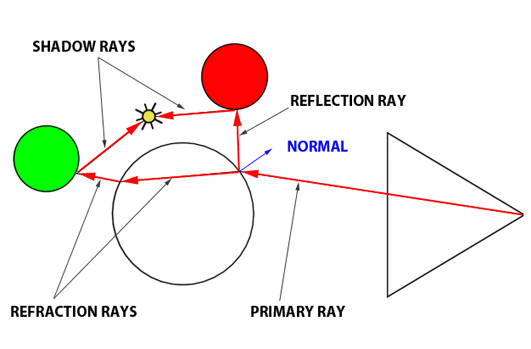
Давайте подведем итог. Как работает алгоритм Уиттинга? Мы пускаем основной луч от глаза к ближайшему пересечению (если таковое имеется) с объектами в сцене. Если луч попадает на объект, который не является рассеянным или непрозрачным, мы должны выполнить дополнительную вычислительную работу. Чтобы вычислить результирующий цвет в этой точке, скажем, стеклянного шара, вам нужно вычислить цвет отражения и цвет преломления и смешать их. Помните, что мы делаем это в три этапа. Вычислите цвет отражения, вычислите цвет преломления, а затем примените уравнение Френеля.

Сначала мы вычисляем направление отражения. Для этого нам нужны два элемента: нормаль в точке пересечения и направление основного луча. Как только мы получим направление отражения, мы выпустим новый луч. Возвращаясь к нашему старому примеру, предположим, что отраженный луч попадает на красную сферу. Используя алгоритм Аппеля, мы определяем, сколько света достигает этой точки на красной сфере, направляя теневой луч на источник света. При этом получается цвет (черный, если он затенен), умноженный на интенсивность света и возвращенный на поверхность стеклянного шара.
Теперь мы проделываем то же самое с преломлением. Поскольку луч проходит через стеклянный шар, его называют передающим лучом (свет прошел с одной стороны сферы на другую; он был передан). Чтобы вычислить направление пропускания, нам нужна нормаль в точке попадания, направление основного луча и показатель преломления материала (в данном примере он может составлять что-то вроде 1,5 для стеклянного материала). При вычислении нового направления преломляющий луч переходит на другую сторону стеклянного шара. И снова, поскольку при этом меняется среда, луч преломляется еще раз. Как вы можете видеть на соседнем изображении, направление луча меняется, когда луч входит в стеклянный объект и выходит из него. Преломление происходит каждый раз, когда происходит смена среды, и две среды, та, из которой выходит луч, и та, в которую он попадает, имеют разный показатель преломления. Показатель преломления воздуха очень близок к 1, а показатель преломления стекла составляет около 1,5. Преломление, для эффекта, слегка искривило луч. Этот процесс приводит к тому, что объекты кажутся смещенными при взгляде сквозь них или на объекты с разными показателями преломления. Давайте представим, что когда преломленный луч покидает стеклянный шар, он попадает в зеленую сферу. Мы вычислили локальную освещенность в точке пересечения зеленой сферы и преломленного луча (путем съемки теневого луча). Затем цвет (черный, если он затенен) умножается на интенсивность света и возвращается на поверхность стеклянного шара
Наконец, мы вычисляем уравнение Френеля. Нам нужен показатель преломления стеклянного шара, угол между основным лучом и нормалью в точке попадания. Используя скалярное произведение (мы объясним это позже), уравнение Френеля возвращает два значения смешивания.
Вот некоторый псевдокод, иллюстрирующий, как это работает:
// просчитываем цвет рефлекции
color reflectionCol = computeReflectionColor();
// также цвет рефракции
color refractionCol = computeRefractionColor();
float Kr; // коэфициент смешивания для рефлекции
float Kt; // а также для рефракции
fresnel(refractiveIndex, normalHit, primaryRayDirection, &Kr, &Kt);
// смешиваем цвета. Обратите внимание, что Kt = 1 - Kr
glassBallColorAtHit = Kr * reflectionColor + Kt * refractionColor;В приведенном выше коде мы написали в комментарии, что Kt = 1 - Kr. Другими словами, Kr + Kt = 1. Это потому, что в природе свет не может быть создан или уничтожен. Следовательно, если часть падающего света отражается, то, что осталось от этого падающего света (та часть, которая не была отражена), обязательно преломляется. Если вы возьмете сумму отраженного и преломленного света, то она будет равна количеству поступающего света. Как правило, уравнение Френеля предоставляет нам значение для Kr и Kt (и если оно работает правильно, их сумма должна быть равна 1), так что вы можете использовать значения, возвращаемые функцией напрямую. Однако этого было бы достаточно, если бы у нас был только один из них. Если бы у вас был Kr, вы могли бы получить Kt (1 - Kr). Если бы у вас было Kt, вы могли бы получить Kr (1 - Kt).
Последняя прекрасная особенность этого алгоритма заключается в том, что он рекурсивный (в некотором смысле это и проклятие!). В случае, который мы изучали до сих пор, отраженный луч попадает на красную непрозрачную сферу, а преломляющий луч попадает на зеленую, непрозрачную и рассеянную сферу. Однако мы представим, что красная и зеленая сферы также являются стеклянными шарами. Чтобы найти цвет, возвращаемый отраженными и преломляющимися лучами, нам пришлось бы проделать с красной и зеленой сферами тот же процесс, который мы использовали с оригинальным стеклянным шаром: то есть направить в сцену еще больше отраженных и преломляющих лучей. Это недостаток алгоритма трассировки лучей, который иногда может стать головной болью. Представьте, что наша камера находится в коробке, у которой есть только отражающие грани. Теоретически, лучи попадают в ловушку и будут продолжать отражаться от стенок коробки бесконечно (или до тех пор, пока вы не остановите моделирование). По этой причине мы должны установить произвольный предел, препятствующий взаимодействию лучей, таким образом, бесконечно повторяясь. Каждый раз, когда луч отражается или преломляется, его глубина увеличивается. Мы останавливаем процесс рекурсии, когда глубина луча превышает максимальную глубину рекурсии. Ваше изображение не обязательно будет выглядеть идеально точным, но лучше иметь приблизительный результат, чем его отсутствие.






