Я занялся изучением процессов распознавания коллизий, и это привело меня к алгоритму Гилберта — Джонсона — Кирти (Gilbert-Johnson-Keerthi, GJK).
Все примеры кода в посте написаны на TypeScript. В примерах используются созданные мной структуры, которые подробно в посте не рассмотрены. Они просты и их можно посмотреть в репозитории GitHub:
VectorIShapeCollision
Весь код из поста хранится в репозитории GitHub:
https://github.com/jthomperoo/gjk-ts-implementation
Пост написан на основании этой статьи и рекомендованного в ней видео:
- http://www.dyn4j.org/2010/04/gjk-gilbert-johnson-keerthi/
- http://mollyrocket.com/849
Введение
GJK — это алгоритм, предназначенный для определения пересечения двух выпуклых фигур. Он прост и реализуется при помощи обобщённой «вспомогательной функции», позволяющей использовать более общий подход — аналогичным образом можно обрабатывать многоугольники и фигуры, состоящие из кривых, например, эллипсы.
Необходимые сведения
Сумма Минковского
В GJK используется концепция под названием «сумма Минковского». СМ вычисляется сложением всех точек двух фигур. Для примера возьмём две показанные ниже фигуры:
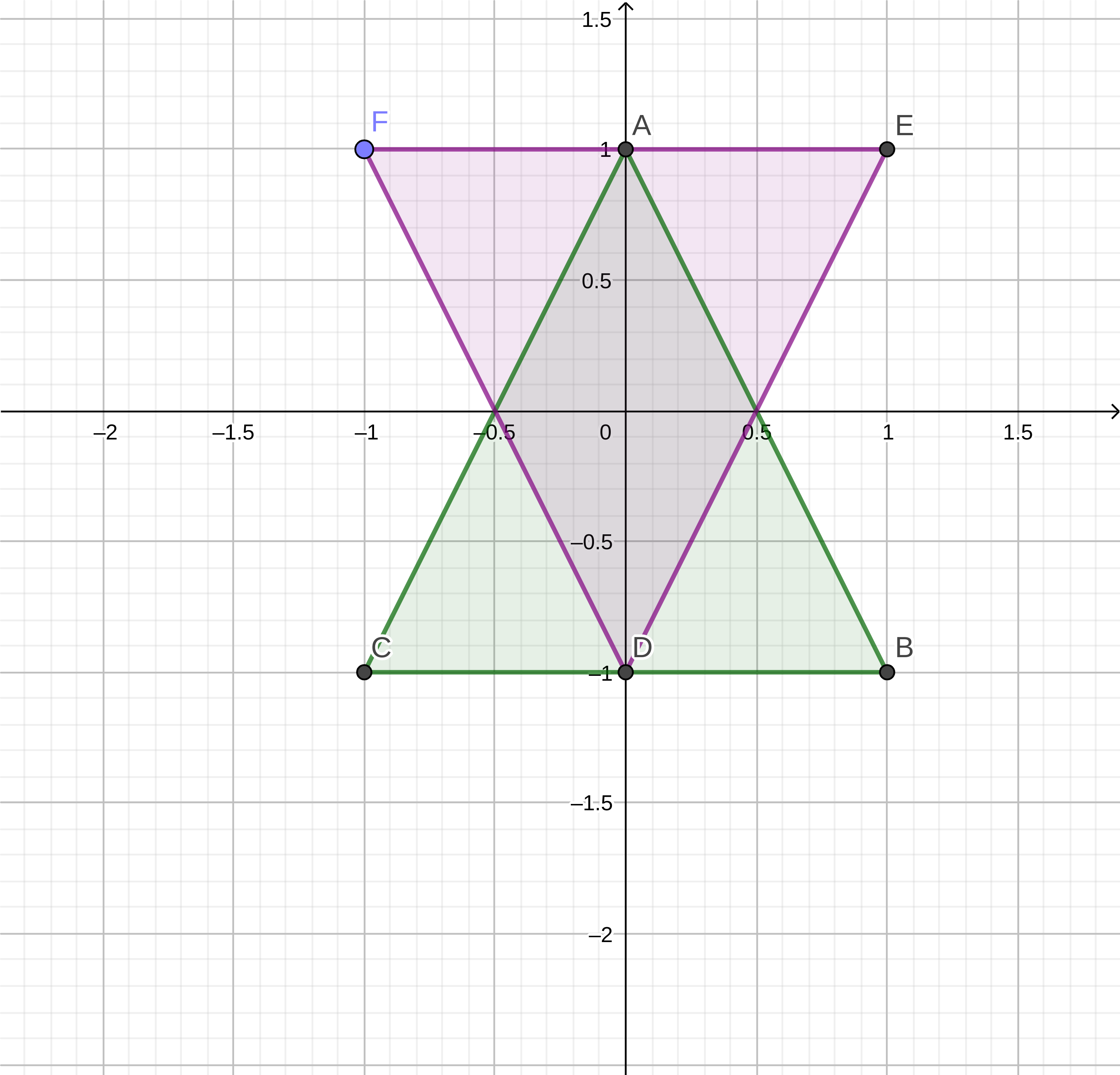
Фигура A (зелёная):
| A | B | C |
|---|---|---|
| (0,1) | (1,-1) | (-1,-1) |
Фигура B (фиолетовая):
| D | E | F |
|---|---|---|
| (0,-1) | (1,1) | (-1,1) |
Взяв значения фигуры A и фигуры B, мы можем вычислить сумму Минковского:
A + D = (0,1) + (0,-1) = (0,0)
A + E = (0,1) + (1,1) = (1,2)
A + F = (0,1) + (-1,1) = (-1,2)
B + D = (1,-1) + (0,-1) = (1,-2)
B + E = (1,-1) + (1,1) = (2,0)
B + F = (1,-1) + (-1,1) = (0,0)
C + D = (-1,-1) + (0,-1) = (-1,-2)
C + E = (-1,-1) + (1,1) = (0,0)
C + F = (-1,-1) + (-1,1) = (-2,0)Если взять эти значения и составить из них график, то увидим, какая фигура получится в результате.
Сумма Минковского для фигур A и B:
Учтите, что AD в таблице и на графике соответствует A + D
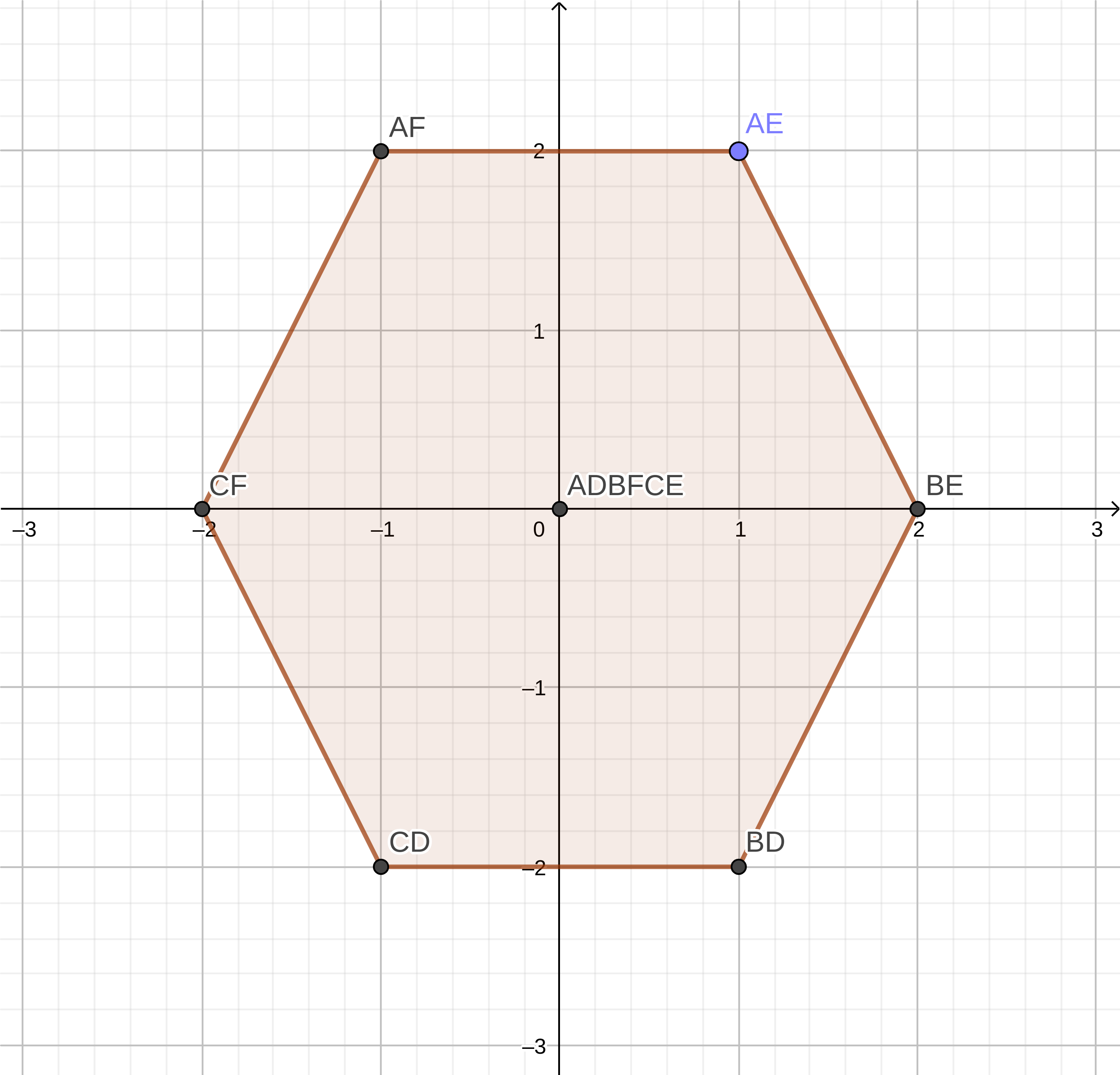
| AD | AE | AF | BD | BE | BF | CD | CE | CF |
|---|---|---|---|---|---|---|---|---|
| (0,0) | (1,2) | (-1,2) | (1,-2) | (2,0) | (0,0) | (-1,-2) | (0,0) | (-2,0) |
Чтобы лучше понять сумму Минковского, можно представить, что мы берём фигуру A и обходим ею контур фигуры B. Получившаяся фигура будет суммой Минковского.
Разность Минковского
GJK использует разновидность суммы Минковского, в которой берётся не A + B, а A — B. В прочитанных мной источниках это называется «разностью Минковского» (Minkowski Difference). Разность Минковского обладает интересным свойством: если две фигуры накладываются/пересекаются, то получившаяся разность Минковского будет содержать точку начала координат. И это является основой алгоритма GJK.
Взяв значения фигур A и B, мы можем вычислить разность Минковского:
A - D = (0,1) - (0,-1) = (0,2)
A - E = (0,1) - (1,1) = (-1,0)
A - F = (0,1) - (-1,1) = (1,0)
B - D = (1,-1) - (0,-1) = (-1,0)
B - E = (1,-1) - (1,1) = (0,-2)
B - F = (1,-1) - (-1,1) = (2,-2)
C - D = (-1,-1) - (0,-1) = (-1,0)
C - E = (-1,-1) - (1,1) = (-2,-2)
C - F = (-1,-1) - (-1,1) = (0,-2)Если мы возьмём эти значения и нанесём их на график, то увидим получившуюся фигуру.
Разность Минковского для фигур A и B:
Учтите, что AD в таблице и на графике относится к A — D
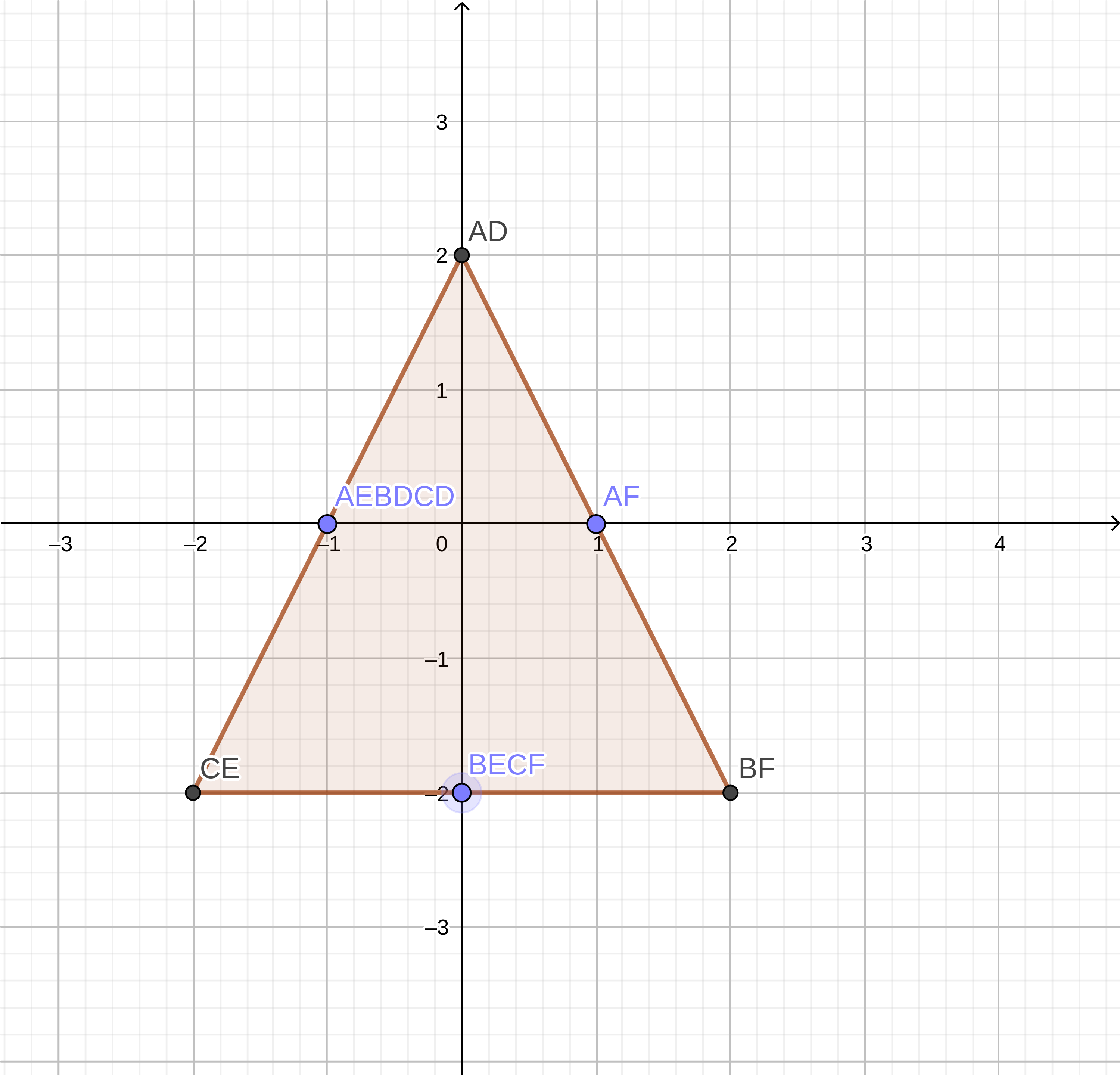
| AD | AE | AF | BD | BE | BF | CD | CE | CF |
|---|---|---|---|---|---|---|---|---|
| (0,2) | (-1,0) | (1,0) | (-1,0) | (0,-2) | (2,-2) | (-1,0) | (-2,-2) | (0,-2) |
Алгоритм
Взяв за основу эти концепции, алгоритм GJK оптимизирует их. Вычисление суммы Минковского может занять много времени, особенно если вы проверяете пересечение двух фигур, состоящих из множества точек. Чтобы избежать этого, GJK использует две ключевые концепции: вспомогательные функции и симплексы.
Вспомогательные функции
Вспомогательные функции — это способ сэмплирования точки на ребре разности Минковского без построения всей фигуры. Вспомогательная функция получает две сравниваемые фигуры, и направление, которое нужно проверить. Затем вспомогательная функция получает от каждой фигуры точку, наиболее удалённую от двух противоположных направлений. При помощи этих двух наиболее удалённых точек можно вычислить вспомогательную точку на фигуре разности Минковского. Мы берём точки с противоположных направлений потому, что получим точку на разности Минковского, которая даст нам наибольшую площадь, то есть будет выше вероятность того, что мы заключим в фигуру точку начала координат. Так как разность Минковского — это
наиболее удалённая точка фигуры a - наиболее удалённая точка фигуры b, наличие точки фигуры b, сэмплированной с противоположного направления, даст нам вспомогательную точку, которая находится максимально далеко в данном направлении.Реализация вспомогательной функции довольно проста:
function support(a: IShape, b: IShape, direction: Vector): Vector {
const aFar = a.FarthestPointInDirection(direction);
const bFar = b.FarthestPointInDirection(direction.Invert());
return aFar.Sub(bFar);
}Одним из преимуществ GJK является то, что
FarthestPointInDirection можно абстрагировать и применить к многоугольникам и кривым. Вот реализация FarthestPointInDirection для многоугольника.class Polygon implements IShape {
public points: Vector[];
...
public FarthestPointInDirection(direction: Vector): Vector {
let farthestDistance = -Infinity;
// If there are no points, just return point 0,0
let farthestPoint: Vector = new Vector(0,0);
for (const point of this.points) {
const distanceInDirection = point.Dot(direction);
if (distanceInDirection > farthestDistance) {
farthestPoint = point;
farthestDistance = distanceInDirection;
}
}
return farthestPoint;
}
}Если вы хотите увидеть, как будут реализованы другие фигуры, то изучите репозиторий Git этого поста, в котором представлена реализация для
Circle.Вот как будет вычисляться вспомогательная точка в направлении (1,0) для фигур A и B:
- Берём наиболее удалённую точку у фигуры A; это оказывается точка B (1,-1). (Её можно вычислить, как это делает показанный выше алгоритм, или просто увидеть, взглянув на график).
- Берём наиболее удалённую точку у фигуры B; это оказывается точка F (-1, 1).
- Вычисляем B — F; это оказывается точка BF (2,-2) — она и будет вспомогательной.
Симплексы
Симплекс — это выборка точек вдоль фигуры разности Минковского. Симплексы могут содержать до трёх точек. GJK использует их, пробуя построить треугольник вокруг точки начала координат, чтобы определить возникновение коллизии.
Построение симплексов
Симплексы строятся итеративно, добавлением вспомогательных точек в разных направлениях. Каждая вспомогательная точка должна указывать в новом направлении, чтобы мы могли как можно быстрее построить симплекс, содержащий точку начала координат. Сложность заключается в выборе направления, в котором следует получать следующую вспомогательную точку.
Определение коллизии и выбор направления
Базовый алгоритм просто строит симплекс при помощи вспомогательной функции, пробуя заключить в фигуру точку начала координат. Мы можем понять, что коллизии/пересечения нет, проверив, достигает ли вычисленная вспомогательная точка точки начала координат, и если не достигает, то точка начала координат должна находится вне разности Минковского; следовательно, мы можем сказать, что коллизии/пересечения нет.
function Calculate(a: IShape, b: IShape): Collision | undefined {
// Build a new Simplex for determining if a collision has occurred
const simplex = new Simplex();
// Choose an arbitrary starting direction
let direction: Vector | undefined = new Vector(0,1);
// Get the first support point and add it to the simplex
const initSupportPoint = support(a, b, direction);
simplex.Add(initSupportPoint);
// Flip the direction for the next support point
direction = direction.Invert();
// Keep iterating until the direction is undefined, this will occur when
// 'CalculateDirection' doesn't return a direction, indicating that an
// intersection has been detected
while(direction) {
const supportPoint = support(a, b, direction);
// If the support point did not reach as far as the origin,
// the simplex must not contain the origin and therefore there is no
// intersection
if (supportPoint.Dot(direction!) <= 0) {
// No intersection
return;
}
// Add the simplex and determine a new direction
simplex.Add(supportPoint);
direction = simplex.CalculateDirection();
}
// No direction calculated, intersection detected
return new Collision(a, b);
}Вся сложность и внутренняя работа алгоритма находятся в
simplex.CalculateDirection. Эта функция определяет, находится ли точка начала координат в текущем симплексе — если это так, она вернёт undefined; в противном случае она вернёт новое направление для получения вспомогательной точки, которую нужно добавить к симплексу.class Simplex {
private points: Vector[];
...
CalculateDirection(): Vector | undefined {
// Get a, the last point added to the simplex
const a = this.points[this.points.length - 1];
// Since a was just added, we know that the inverse of a points
// towards the origin
const ao = a.Invert();
// If the simplex is a triangle
if (this.points.length == 3) {
// B is the penultimate in the simplex
// C is the oldest point in the simplex
const b = this.points[1];
const c = this.points[0];
// Determine a->b and a->c lines
const ab = b.Sub(a);
const ac = c.Sub(a);
// Determine perpendicular of the a->b line
let abPerp = new Vector(ab.y, -ab.x);
// Check the handedness of the perpendicular, it should
// face AWAY from the simplex
if (abPerp.Dot(c) >= 0) {
abPerp = abPerp.Invert();
}
// If the origin lies outside of the simplex remove the
// point and determine a new direction in the direction
// of the perpendicular; aiming to try to encapsulate
// the origin that lies outside
if (abPerp.Dot(ao) > 0) {
this.points.splice(0, 1);
return abPerp;
}
// Determine perpendicular of the a->c line
let acPerp = new Vector(ac.y, -ac.x);
// Check the handedness of the perpendicular, it should
// face AWAY from the simplex
if (acPerp.Dot(b) >= 0) {
acPerp = acPerp.Invert();
}
// If the origin lies outside of the simplex remove the
// point and determine a new direction in the direction
// of the perpendicular; aiming to try to encapsulate
// the origin that lies outside
if (acPerp.Dot(ao) > 0) {
this.points.splice(1, 1);
return acPerp;
}
return undefined;
}
// Otherwise the simplex is just a line
// B is the penultimate point in the simplex,
// in this case the other end of the line
const b = this.points[0];
// Determine a -> b line
const ab = b.Sub(a);
// Get the perpendicular of the a->b line
let abPerp = new Vector(ab.y, -ab.x);
// Check the handedness of the perpendicular, it should
// face TOWARDS the origin
if (abPerp.Dot(ao) <= 0) {
abPerp = abPerp.Invert();
}
return abPerp;
}
}Вы можете задаться вопросом: почему мы не проверяем отрезок BC? Потому что мы можем безоговорочно исключить, что точка начала координат находится вдоль её перпендикуляра. Поскольку точки B и C уже находятся в симплексе, и добавлены они не только что, мы знаем, что их проверяли в предыдущей итерации. Проверять их могли или как часть треугольника, или как отрезок из первых двух точек в симплексе — это не имеет значения. Поэтому мы спокойно можем пропустить проверку отрезка BC.
Подробное объяснение
У нас получилось много кода, и он выглядит запутанно. Ниже я по шагам разберу все этапы алгоритма для показанных выше фигур A и B.
Точки фигур A и B:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| (0,1) | (1,-1) | (-1,-1) | (0,-1) | (1,1) | (-1,1) |
- Подготовка алгоритма; в качестве начального направления берём
(0,1).
// Build a new Simplex for determining if a collision has occurred const simplex = new Simplex(); // Choose an arbitrary starting direction let direction: Vector | undefined = new Vector(0,1);
- Получаем первую вспомогательную точку.
// Get the first support point and add it to the simplex const initSupportPoint = support(a, b, direction); simplex.Add(initSupportPoint); // Flip the direction for the next support point direction = direction.Invert();
Получаем наиболее удалённую точку от точки A в направлении(0,1)и от точки B в направлении(0,-1).
aFar:(0,1)и bFar:(0,-1)
Используем эти значения, чтобы получить вспомогательную точку.
Support: aFar-bFar =(0,2)
function support(a: IShape, b: IShape, direction: Vector): Vector { const aFar = a.FarthestPointInDirection(direction); const bFar = b.FarthestPointInDirection(direction.Invert()); return aFar.Sub(bFar); }
- Переворачиваем направление для следующей вспомогательной точки и начинаем итерации, вычисляя новую вспомогательную точку.
Support:(0,-3)
// Flip the direction for the next support point direction = direction.Invert(); // Keep iterating until the direction is undefined, this will occur when // 'CalculateDirection' doesn't return a direction, indicating that an // intersection has been detected while(direction) { const supportPoint = support(a, b, direction); - Проверяем, достигла ли вспомогательная точка точки начала координат; если нет, то пересечения быть не должно. Если она достигла точки начала координат, то добавляем точку в симплекс.
В данном случае вспомогательная точка достигла точки начала координат.
direction:(0,-1)
Support:(0,-3)
supportPoint.Dot(direction):3
// If the support point did not reach as far as the origin, // the simplex must not contain the origin and therefore there is no // intersection if (supportPoint.Dot(direction!) <= 0) { // No intersection return; } // Add the simplex and determine a new direction simplex.Add(supportPoint);
- На этом этапе симплекс представляет собой отрезок, поэтому не может содержать внутри точку начала координат; определяем новое направление, в котором нужно искать вспомогательную точку.
direction = simplex.CalculateDirection();
- Берём последнюю точку, добавленную к симплексу, и определяем направление к точке начала координат, это будет величиной, обратной к этой точке.
a:(0,-3)ao:(0,3)
CalculateDirection(): Vector | undefined { // Get a, the last point added to the simplex const a = this.points[this.points.length - 1]; // Since a was just added, we know that the inverse of a points // towards the origin const ao = a.Invert(); // If the simplex is a triangle if (this.points.length == 3) { - Так как симплекс — это отрезок, а не треугольник, берём вторую точку отрезка и вычисляем отрезок симплекса.
b:(0,2)ab:(0,5)
// Otherwise the simplex is just a line // B is the penultimate point in the simplex, // in this case the other end of the line const b = this.points[0]; // Determine a -> b line const ab = b.Sub(a); - Вычисляем перпендикуляр к этому отрезку и проверяем, что он направлен к точке начала координат. Это будет новым направлением для следующей вспомогательной точки.
abPerp:(5, 0)
abPerp.Dot(ao)0
abPerp:(-5, 0)
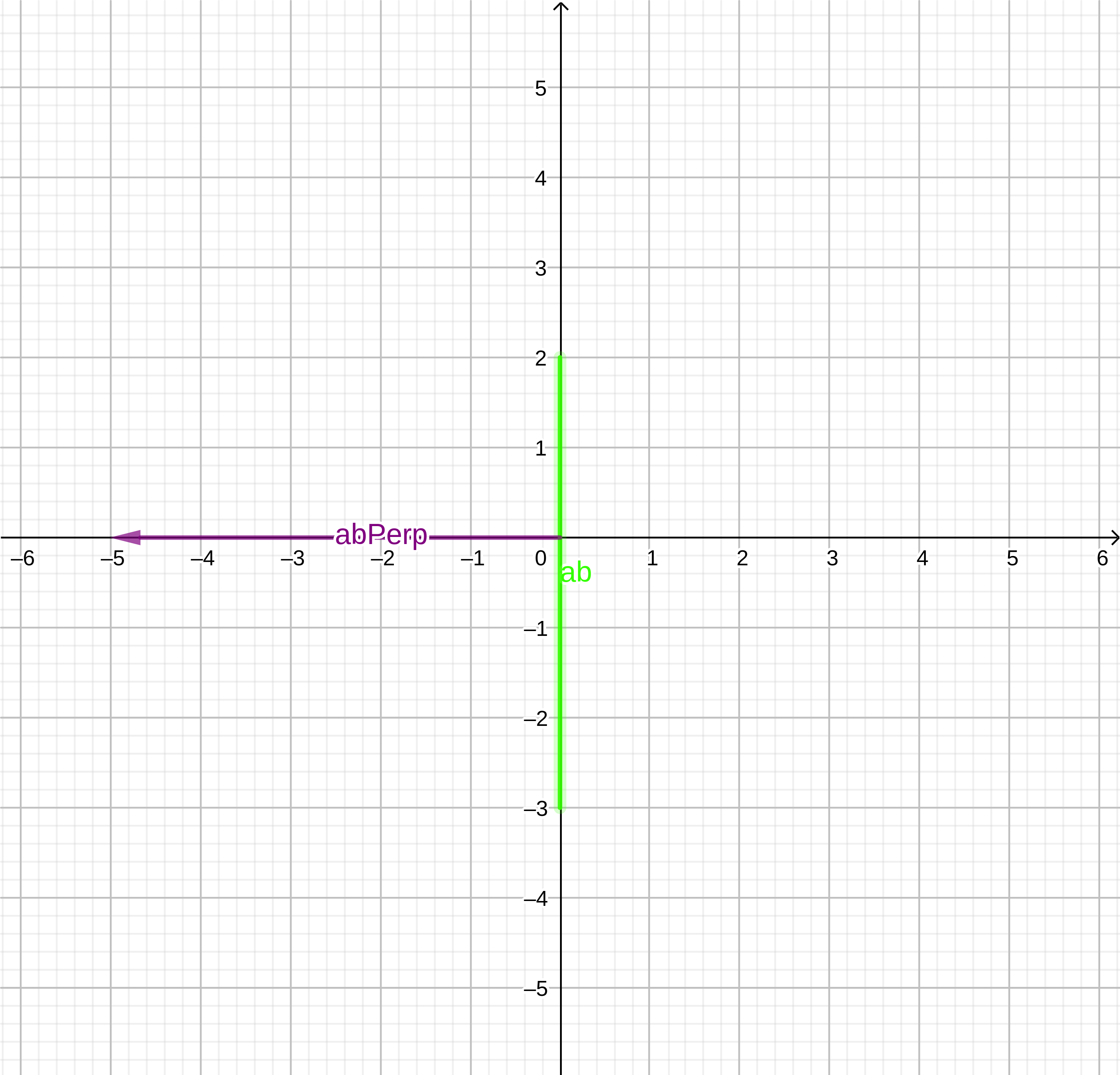
// Get the perpendicular of the a->b line let abPerp = new Vector(ab.y, -ab.x); // Check the handedness of the perpendicular, it should // face TOWARDS the origin if (abPerp.Dot(ao) <= 0) { abPerp = abPerp.Invert(); } return abPerp;
- Берём последнюю точку, добавленную к симплексу, и определяем направление к точке начала координат, это будет величиной, обратной к этой точке.
- Теперь у нас есть направление для поиска следующей вспомогательной точки. Мы возвращаемся к началу цикла и не выходим из него, ведь пока у нас есть направление, а пересечение ещё не найдено.
direction:(-5, 0)
Support:(-2,-2)
supportPoint.Dot(direction):10
Вспомогательная точка достигла точки начала координат, поэтому мы не можем сказать, что пересечения нет.
while(direction) { const supportPoint = support(a, b, direction); // If the support point did not reach as far as the origin, // the simplex must not contain the origin and therefore there is no // intersection if (supportPoint.Dot(direction!) <= 0) { // No intersection return; } - Добавляем в симплекс новую вспомогательную точку, создавая треугольник. Этот треугольник может содержать точку начала координат, и если это так, то симплекс вернёт
undefined, а не новое направление для поиска.
// Add the simplex and determine a new direction simplex.Add(supportPoint); direction = simplex.CalculateDirection();
- Берём точки симплекса треугольника.
a:(-2,-2)b:(0,-3)c:(0,2)ao:(2,2)
// Get a, the last point added to the simplex const a = this.points[this.points.length - 1]; // Since a was just added, we know that the inverse of a points // towards the origin const ao = a.Invert(); // If the simplex is a triangle if (this.points.length == 3) { // B is the penultimate in the simplex // C is the oldest point in the simplex const b = this.points[1]; const c = this.points[0]; - Берём отрезки ab и ac.
ab:(2,-1)ac:(2,4)
// Determine a->b and a->c lines const ab = b.Sub(a); const ac = c.Sub(a); - Вычисляем перпендикуляр к отрезку ab, направленный от симплекса.
abperp:(-1,-2)
// Determine perpendicular of the a->b line let abPerp = new Vector(ab.y, -ab.x); // Check the handedness of the perpendicular, it should // face AWAY from the simplex if (abPerp.Dot(c) >= 0) { abPerp = abPerp.Invert(); } - Определяем, находится ли точка начала координат вне симплекса за ab.
abPerp.Dot(ao):-6
Точка начала координат не лежит вне симплекса за ab.
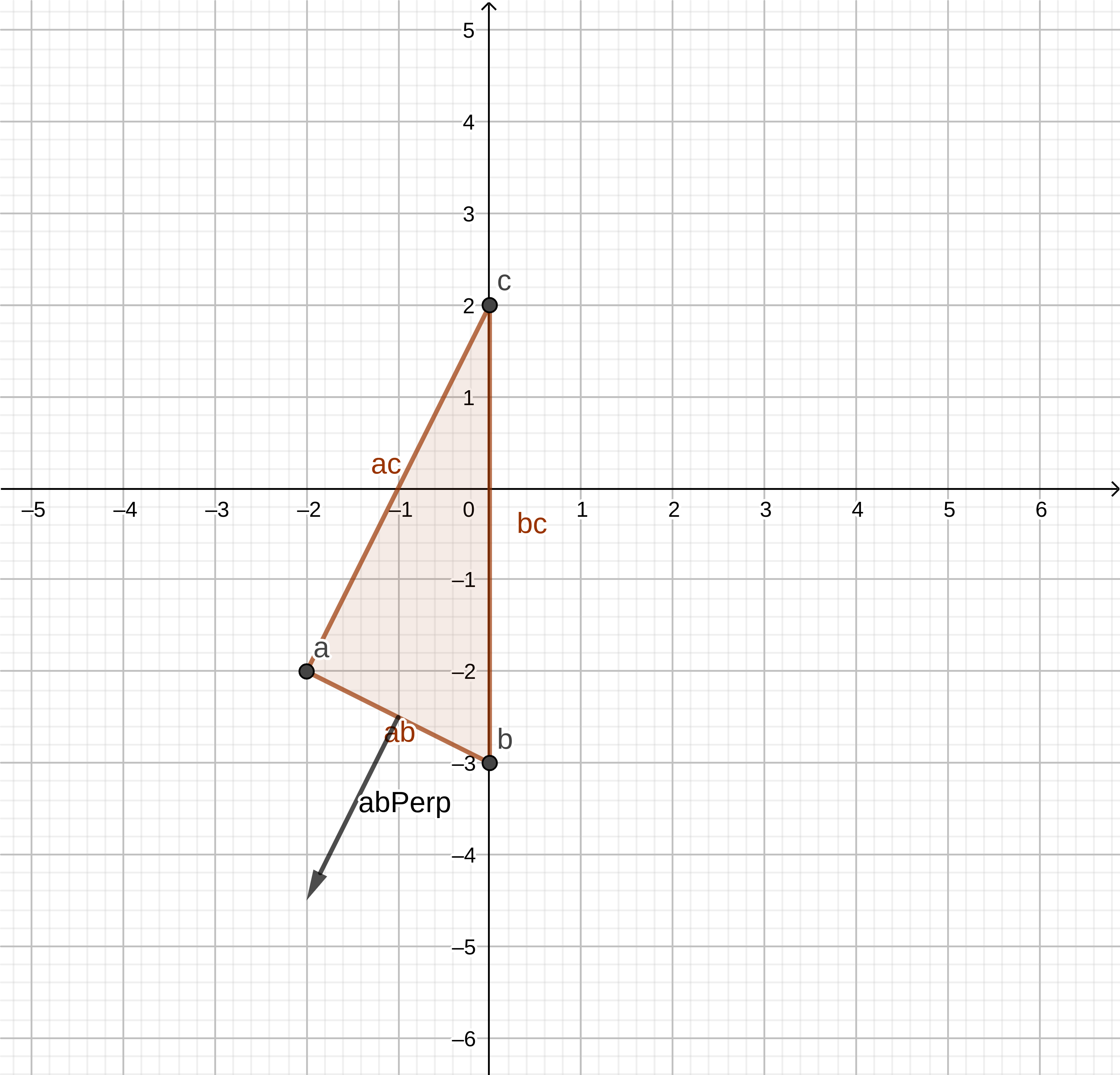
if (abPerp.Dot(ao) > 0) { this.points.splice(0, 1); return abPerp; } - Вычисляем перпендикуляр к отрезку ac, направленный от симплекса.
acPerp:(-4,2)
// Determine perpendicular of the a->c line let acPerp = new Vector(ac.y, -ac.x); // Check the handedness of the perpendicular, it should // face AWAY from the simplex if (acPerp.Dot(b) >= 0) { acPerp = acPerp.Invert(); } - Определяем, находится ли точка начала координат снаружи симплекса за ac.
acPerp.Dot(ao):-4
Точка начала координат не находится снаружи симплекса за ab.

// If the origin lies outside of the simplex remove the // point and determine a new direction in the direction // of the perpendicular; aiming to try to encapsulate // the origin that lies outside if (acPerp.Dot(ao) > 0) { this.points.splice(1, 1); return acPerp; } - Так как в этой итерации были проверены AB и AC, и мы знаем, что BC был проверен в предыдущей итерации, то точка начала координат должна лежать внутри симплекса, поэтому коллизия/пересечение обнаружено — сообщая об этом, функция вернёт
undefined.
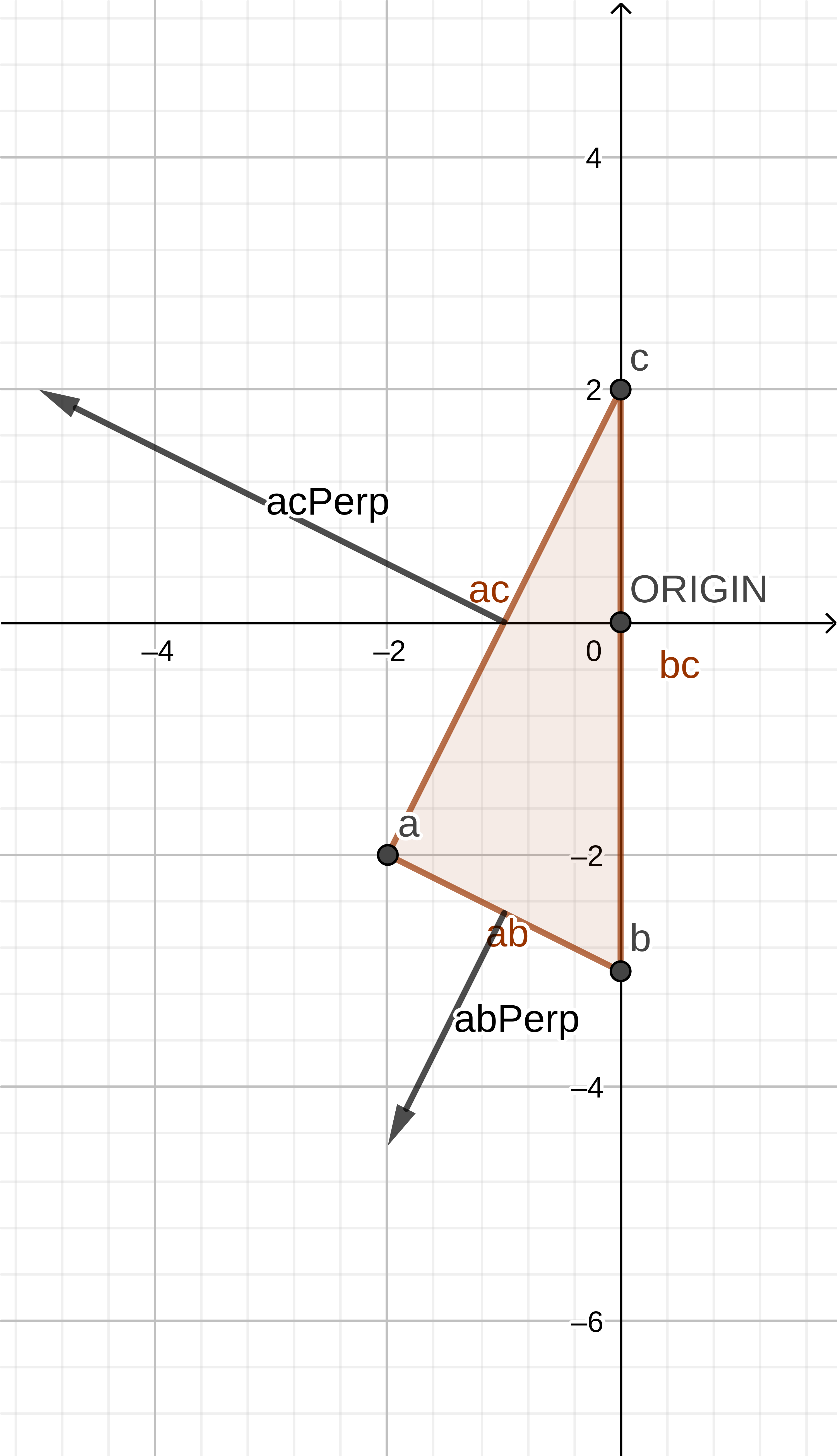
- Берём точки симплекса треугольника.
- Так как коллизия была обнаружена, выполняется выход из цикла и возвращается информация
Collisionо коллизии между двумя фигурами.
direction = simplex.CalculateDirection(); } // No direction calculated, intersection detected return new Collision(a, b);
Заключение
Надеюсь, эта статья поможет вам разобраться в алгоритме GJK. Алгоритм даёт ответ «да/нет» о наличии коллизии между двумя фигурами. Работающий пример с многоугольниками и кругами можно посмотреть в репозитории к этому посту. Вы сможете расширить этот код дополнительными алгоритмами и техниками, попробовав получить расстояние проникновения между двумя фигурами, нормали коллизии и точки контакта. В посте dyn4j есть ссылки на хорошие ресурсы по различным алгоритмам распознавания коллизий/ответов; если вы хотите расширить GJK, то стоит их изучить.





