Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В статье утверждается: фазовое пространство состояний не обязательно должно быть выражено числовыми зависимостями; что сложные объекты могут быть иерархически выстроены на основе переменных, каждая из которых принимает значение своего пространства состояний; что состояния одного могут влиять на состояния другого. И все выше представленное может быть в качестве состояния чего-либо еще.
Р. Эшби описал в [Введение в кибернетику] как могут быть соединены преобразователи для случая, когда состояния одного влияют на параметры другого преобразователя. Терминология в этой статье несколько иная: более привычная в среде программирования (действие, состояние) и вместо преобразователя употребляется термин таблица. Новизна же в том, что показано как одну таблицу можно вложить в другую: текущее состояние таблицы подставляется в переменную (имя самой таблицы), а уже она может быть состоянием или действием какой-либо иной таблицы.
Требования к описанию объекта: быть управляемым, быть масштабируемым и быть описанным в терминах сменяющихся состояний. Основа логики:
Используется алгебраическая запись Y=F(X), где Х – текущее состояние, Y – следующее состояние, F – действие, переводящее состояние их Х в Y.
Поскольку (действие, состояние) - множество, будем кодировать такие переходы в числах (так удобней). Например, 12=31(15) 11=32(12) означает, что текущее состояние 15 при действии 31 переходит в следующее состояние 12, которое становится текущим; далее текущее состояние 12 при действии 32 переходит в состояние 11. Запись NaN=31(12) означает, что неизвестно следующее состояние из 12 при действии 31.
Не всегда переходы однозначны. Запись 45|44|41=32(12) означает, что из состояния 12 при действии 32 следующим состоянием будет либо 45, либо 44, либо 41.
Нет ограничения на подстановки. Запись 44=36(41) 53=44(52) означает, что полученное состояние 44 является действием для перехода из состояния 52 в состояние 53.
Такие переходы более удобно собирать в таблицы. Причем имя таблицы будет служить переменной, куда подставляется текущее состояние этой таблицы. И уже сама эта переменная будет подставляться в состояние (или действие) другой таблицы.
Главное, что такой способ описания достаточно универсален, если речь идет о дискретных переходах. Чтобы представить, вообразим такой пример. Пусть объект (таблица) белая монета представлен переходами: если повернуть, то орел перейдет в решку, а решка перейдет в орел; если не поворачивать, то орел переходит в себя же, как и решка. Пусть имеются еще желтая монета и красная монета. Итак, перед нами 3 таблицы. В каждой из которых два возможных состояния и два возможных действия. В этой статье не рассматривается, но совокупность текущих состояний каждой таблицы можно принимать за вектор. Пусть текущими состояниями будут: (решка белой монеты, орел красной монеты, орел желтой монеты). Тогда совокупность этих векторов тоже можно понимать, как совокупность состояний, где каждое состояние есть вектор.
Можно рассмотреть наиболее значимые способы соединения таблиц:
Никакое состояние или действие таблицы не влияет на состояние или действие другой таблицы
Состояние орел белой монеты является таблицей красная монета. Иначе говоря, вместо переменной красная монета будет подставляться состояние либо орел красной монеты, либо решка красной монеты. А переменная красная монета будет подставляться вместо состояния орел белой монеты. В результате получим, что белая монета, если ее вращать, например, будет видеться нам то белой решкой, то другой стороной. И та другая сторона будет являться либо красным орлом, либо красной решкой. Здесь приведено такое же различие, как целое (белый орел) и сменяющиеся состояния, характеризующие это целое (красный орел/красная решка).
Теперь соединим белую монету и желтую монету таким образом, что состояния белой будут являться действиями желтой монеты: если белая решка, то вращать желтую монету; если белый орел, то не вращать желтую монету. Кроме того, допустим, что при вращении желтой монеты, если ее текущее состояние орел, то следующим состоянием может быть, как решка, так и орел.
Когда мы видим мир, мы не можем наблюдать все сразу. Выборочное внимание означает, что в отдельный момент времени нам доступно, например, состояние белой монеты, состояние желтой и действия красной. В другой момент времени, например, этими данными могут быть: состояние красной и действия желтой. Возникает вопрос: как из этого хаоса (из этого потока данных) выявить, что имеются эти три таблицы и что они соединены между собой именно таким образом?
Ниже и поэтапно демонстрация работы такой логики. Введем обозначения: 10 – белая монета, 11 – решка белой монеты, 12 – орел белой монеты, 14 – вращать белую монету, 15 – не вращать белую монету. 20 – красная монета, 21 – решка красной монеты, 22 – орел красной монеты, 24 – вращать красную монету, 25 – не вращать красную монету. 30 – желтая монета, 31 – решка желтой монеты, 32 – орел желтой монеты, 34 – вращать желтую монету, 35 – не вращать желтую монету.
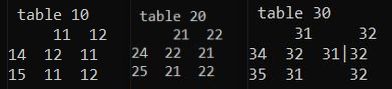
Исходные данные представлены на рис.1 и собраны в 3 таблицы: таблица 10, таблица 20, таблица 30. Верхняя строка каждой таблицы отображает одно из возможных текущих состояний, левый столбец таблицы ее возможное действие. Например, для таблицы 10 текущим может быть одно из состояний {11, 12}, а действием может быть {14, 15}. На пересечении текущего состояния и действия – следующее состояние. Так, для таблицы желтая монета: 31|32=34(32) из состояния 32 при действии 34 следующим состоянием будет либо 31, либо 32.
Как все работает? Пусть имеется объект исследования, состоящий из этих таблиц определенным образом соединенных. Программа берет каждую таблицу и случайно генерирует действия для каждой таблицы. В зависимости от текущих состояний получаем следующие. Эти текущие состояния и действия поступают на вход другой части программы. И уже она пытается понять какие таблицы генерируют эти данные и как эти таблицы могут быть соединены.
На рис.2 показано как можно управлять программой через параметры метода observation (n – количество наблюдений, connect_sf – разрешить соединение типа состояние-действие, connect_tsf – разрешить соединение типа таблица-состояние/действие, noise - величина шума, shuffle – перемешивать значения столбцов, to_people – демонстрация пользователям как видит алгоритм поток данных).

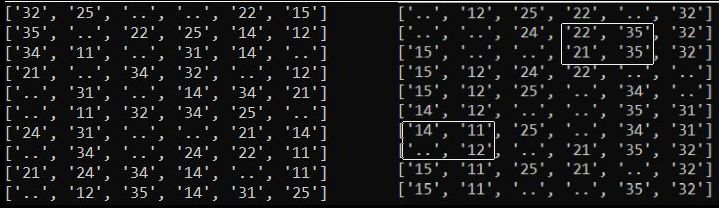
На рис.3 представлен поток данных в таком виде, как его видит программа. Каждая строка соответствует единичному наблюдению. Количество столбцов – количество переменных. В данном случае их шесть (три таблицы и в каждой таблице текущее состояние и выбранное действие). На этом рисунке в левой таблице представлен поток данных в наиболее сложном для анализа виде. Величина шум=2 означает, что количество ненаблюдаемых состояний (для удобства представлены “..”, а не NaN) не более двух. Но основная трудность не в этом. В том, что состояния и действия могут быть отнесены к разным переменным. По потоку данных 1-ой переменной видно, что ее состояния берутся из множества {32, 35, 34, 21, 24}. Это означает, что здесь намешан вывод 4-х переменных из рис.1: состояния таблицы 30 {32}, действия таблицы 30 {35, 34}, состояния таблицы 20 {21}, действия таблицы 20 {24}.
Единственный способ справится с такой проблемой, выработать гипотезы: какие состояния и действия к каким переменным отнести. Иначе говоря, стоит задача отсортировать состояния и действия в каждой строке потока данных по нужным переменным. Пусть такой гипотезой будет: 1-я переменная {14, 15}, 2-я переменная {11, 12}, 3-я переменная {24, 25}, 4-я переменная {21, 22}, 5-я переменная {34, 35}, 6-я переменная {31, 32}. Затем уже проверять по алгоритму, представленному ниже. Первый выделенный прямоугольник можно интерпретировать так: 35=22(35) из состояния 35 при действии 22 следует состояние 35; 21=35(22) из состояния 22 при действии 35 следует состояние 21. Аналогичны рассуждения по-другому выделенному: 12=14(11) из состояния 11 при действии 14 следует состояние 12. Какие переменные попарно проверять? Все или выборочно – это вопрос времени и ресурсов.
Будем записывать такие единичные переходы Y=F(X) в таблицы. Получим некоторое их количество. Например, такие как на рис.4 и на рис.5. Разница между ними в том, что на рис.4 отображены верные гипотезы, на рис.5 неверные. Верные потому, что анализируются: действия {14, 15} и состояния {12, 11}, что соответствует таблице 10 рис. 1; действия {34, 35} и состояния {32, 31}, что советует таблице 30 рис. 1. Неверные потому, что анализируются действия и состояния, которые не соответствуют ни одной из таблиц рис. 1.
Необходимо пояснить: в круглых скобках под ними приведена оценка каждой таблицы (коэффициент однозначности, коэффициент известности, размер таблицы). Размер таблицы подсчитывается перемножением количества действия на количество состояний. Коэффициент известности – это отношение количества NaN к размеру таблицы. Коэффициент однозначности рассчитывается как отношение количества, как если бы все переходы были однозначны, к всем случившимся переходам. При подсчете коэффициента однозначности NaN не учитываем. Например, рассмотрим четвертую таблицу на рис.4. Количество возможных однозначных переходов было бы 4, а количество вообще наблюдаемых переходов 5. На 1 больше, поскольку из состояния 32 при действии 34 наблюдаем либо следующее состояние 32, либо следующее 31. Находим отношение: 4/5. Для 1 же таблицы — это отношение 3/3. Здесь всего 3 возможных однозначных перехода (NaN не учитываем) и число случившихся переходов тоже 3.

Есть еще одна большая разница между рис.4 и рис.5: если число наблюдений увеличить, то коэффициент однозначности для верных гипотез будет стремится к 1, а для неверных его значение наоборот будет уменьшаться. Разумеется, не для каждой таблицы его максимальное значение будет равно единице. Для таблицы 4 рис. 4 его максимальное значение 0.8, поскольку есть неоднозначность в самой таблице 30 рис. 1, на основании чего данные были сгенерированы и где неоднозначность изначально имелась.

Теперь изменим параметр connect_tsf с False на True. Это значит, переменная 20 будет подставляться вместо состояния 12 таблицы 10. рис. 1. Какая таблица и как соединена описано в отдельной таблице соединений. И при активации параметра connect_tsf делаются соответствующие соединения.
Видно по потоку данных на рис. 6, что значение 2-ой переменной принимает три значения {22, 11, 21}. Ранее до подстановки значение 2-ой переменной на рис. 3 принимало два значения {12, 11}. Видно, что размер таблицы 1 на рис. 6 по сравнению с таблицей 10 рис. 1 после наблюдения увеличился. Из потока данных на рис. 6 видно также, что состояния таблицы 10 рис. 1 и действия таблицы 30 рис. 1 пока не соединены (здесь рассматривается именно мгновенное соединение, а не со сдвигом по времени). Это так, поскольку из состояния 12, т. е. из сменяющихся состояний 21 и 22 следует более одного действия 5-ой переменной: если 12, то либо 35, либо 34. Разница первой и третей таблицы на рис.6 в том, что третья таблица характеризует большее число наблюдений: ушли NaN. Если предположить, что 21 и 22 это состояния какой-то таблицы, то можно сделать замену: переменная 66 (случайно выбранное наименование переменой и отличающее от всех состояний и действий таблицы). Тогда таблица с характеристиками (0.667, 1.0, 6) преобразуется в однозначную. Далее алгоритм пробует разобраться с таблицей 66 и ее состояниями 21 и 22. Если находит действия, такие что и эта таблица однозначна, то задача решена. По сути он приходит к выводу, что таблица 66 – это та же таблица, что и 20 рис. 1. Но при анализе потока данных программа изначально этого не ведала. Она просто сделала вывод: если допустить, что существует состояние 66, то переходы таблицы, в которой представлены действия {14, 15} и состояния {11, 66}, то она однозначна. А если так, то можно попробовать найти действия, для которых таблица 66 с состояниями {21, 22} были бы тоже однозначна.

Так программа упорядочивает данные, так она среди хаоса поступающей информации начинает видеть отдельные сущности. И двигатель ее в этом – максимизация коэффициента однозначности насколько это возможно. В этом смысле она является машиной предсказания. По известным таблицам и их соединениям может получить то или иное состояние определенной таблицы, перемещаясь в пространстве состояний (порой иерархически устроенных) до выбранной цели.
Чуть более сложный случай представлен на рис.7 из статьи.
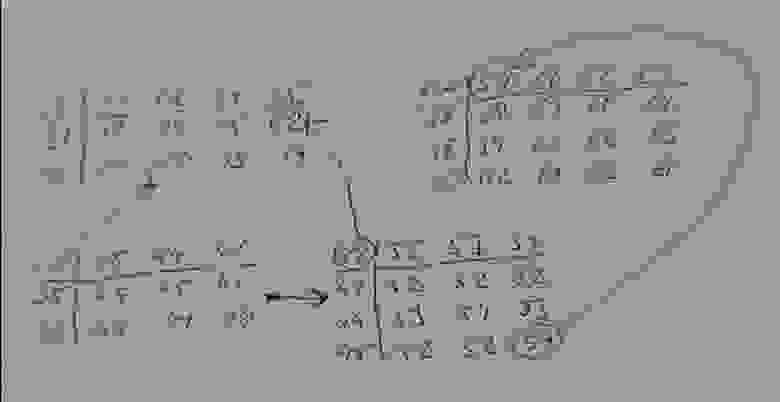
Здесь в таблицу (Л - лабиринт) встраиваются две таблицы: 11 (ключ) и 12 (дверь), которые принадлежат лабиринту. Сначала алгоритм выискивает отдельные сущности, т.е. таблицы с высокой однозначностью. А затем, зная какие таблицы и как соединены, перемещается к выбранной цели: в лабиринте идет к ключу; открывает ключом дверь; идет к открытой двери; через открытую дверь проходит в комнату; в комнате идет к кладу.
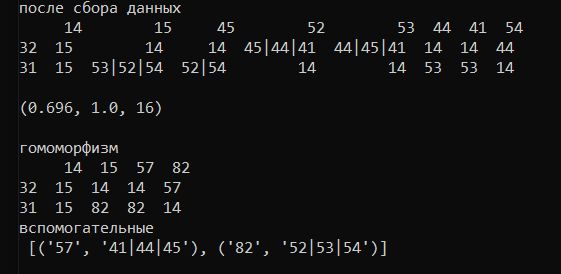
На рис. 8 отображено, что таблица лабиринта программе видится как действия {32, 31} и состояния {14, 15, 57, 82}. Причем состояние 57 предполагает, как таблицу с какими-то действиями и состояниями {41, 44, 45}, а о состоянии 82 она думает, как о таблице, в которой есть возможные состояния {52, 53, 54} при наличии каких-то действий.
Результат: продемонстрировано (на примере программы) новое понимание математических структур, которые могут быть не только соединены так, как это описано в книге Эшби, но еще быть вложенными, что дает неограниченные возможности по конструированию сложных объектов.
Есть на постнауке лекция на тему иерархического обучения с подкреплением А. Панова с МФТИ. В ней, в частности, говорится: "Одна из проблем в иерархическом обучении с подкреплением заключается в том, что нам заранее нужно задавать подцели". Подцели и есть разбиение общей задачи (потока данных с какой-то целью, порой даже неизвестной) на отдельные таблицы.
P.S. Пишите bvv2311@mail.ru






