
Диспозиция
Зимой мы с коллегами решили поучаствовать в хакатоне Power BI, который проводил один крупный российский портал, посвященный этой BI-системе. Задачей было создание аналитического отчёта о посещении сайта портала. На тот момент мы активно использовали в работе shape maps или карты фигур и нам, естественно, захотелось сделать красивую визуализацию метрик в разрезе географии. Карта была собрана и загружена в отчёт, таблица атрибутов подключена в модели, мера, рассчитывающая интересующий нас показатель (посещения сайта), добавлена на карту и тут нас ждал неприятный сюрприз.

Карта получилась бледной и неинформативной. Выделялись лишь пара ярких пятен: Москва и Санкт-Петербург. Проблема была очевидна: две столицы "оттянули" на себя большую часть посещений сайта, оставив регионы далеко позади. В результате различия внутри основной массы наблюдений оказались настолько слабыми, что условное форматирование при помощи цвета, оказалось абсолютно ненаглядным. Говоря языком статистики, мы столкнулись с выбросами, которые сильно отстояли от основной кривой распределения признака по выборке. Воспользуемся возможностями R, чтобы посмотреть, что из себя представляет наша выборка.

На графике мы видим три выброса, которые и мешают нам раскрасить нашу карту. Кстати, подобная ситуация часто встречается и при заливке таблиц, когда одно значение на порядок отличается от всего массива и полыхает красным (или зеленым), а остальные ячейки окрашиваются в диаметрально противоположный цвет. Посмотрим, как будет выглядеть кривая распределения без них.

Кажется, что в таком виде все должно работать нормально. Как же устранить эту проблему? Первое, что приходит в голову - удалить выбросы. Но тогда мы потеряем часть данных, и картина будет неполной. Второй вариант - искусственно занизить значения выбросов так, чтобы визуально они все равно остались в топе. Но на сколько занижать? И как? Об этом и расскажу дальше.
Основной ход сражения
Вариант с "подменой" выбросов на другие, подходящие для целей условного форматирования значения, нам понравился. Оставалось только понять, что использовать в качестве "муляжа". В процессе обсуждения звучали разные версии, но все они были нежизнеспособны и отметались практически сразу. Тут-то и вспомнились мне такие далекие, но знакомые слова - "границы доверительного интервала". Как мы знаем, доверительный интервал, в самом простом изложении - это та часть выборки, которая с заданной вероятностью репрезентативна генеральной совокупности.
Может показаться, что в нашем случае никакой выборки нет, ведь мы располагаем всеми существующими данными о посещениях нашего сайта, то есть, фактически имеем в своем распоряжении всю генеральную совокупность. Однако, такая логика будет оправдана лишь в том случае, когда пользователь отчета будет работать со всеми данными без применения каких-либо фильтров. Но, в реальности, такое встречается редко и пользователи рассматривают лишь часть данных, применяя самую разнообразную фильтрацию. Следовательно, использовать понятие "выборка", применительно к данным отчетов, абсолютно справедливо.
Что если заменить наши выбросы на значение верхней границы доверительного интервала? В теории, если мы выберем 99% доверительный интервал, то получим 99,5% значений нашей выборки в нетронутом виде и лишь 0,5% в искаженном. Что ж, попробуем это реализовать.
Мы имеем следующую модель данных:
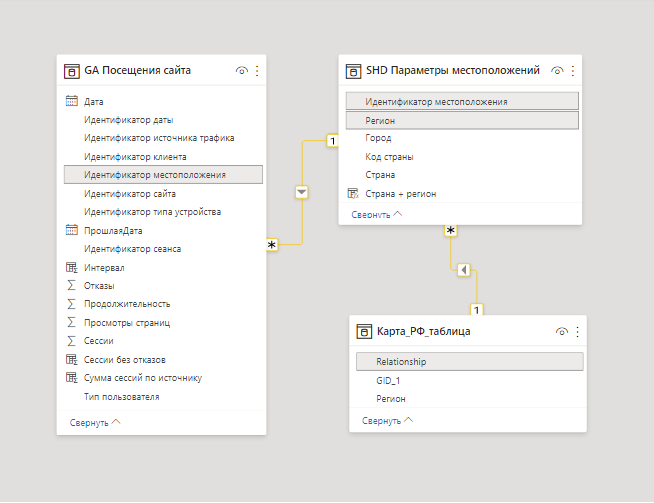
Таблица фактов, где хранятся данные о посещениях сайта, справочник местоположений, связанный с предыдущей таблицей по ID и таблица атрибутов для нашей карты. В последней хранится служебное поле с наименованием полигона в JSON (GID_1), поле с наименованиями регионов, записанными транслитом как в справочнике (Relationship) и поле с наименованиями регионов для отображения на карте (Регион). Расчеты будем производить в мере. Чтобы определить верхнюю границу доверительного интервала, нам нужно прибавить значение интервала к среднему. Что ж, приступим.
Количество_сессий =
var Table_sessions = /* в первой переменной рассчитаем количество
посещений в разрезе регионов */
FILTER(
SUMMARIZE( /* создаем временную таблицу */
FILTER('GA Посещения сайта'; /* оставляем только данные из России */
RELATED('SHD Параметры местоположений'[Страна]) = "Russia");
'SHD Параметры местоположений'[Регион];
/* группируем данные по регионам */
"Sessions"; /* создаем новое поле */
SUM('GA Посещения сайта'[Сессии])); /* агрегируем нужный показатель */
NOT('SHD Параметры местоположений'[Регион] in {""; BLANK()}))
/* убираем строки с пустым регионом */
var All_table_sessions = /* во второй переменной убираем контекст
карты, чтобы рассчитать доверительный интервал для всей выборки */
CALCULATETABLE(
FILTER(
SUMMARIZE(
FILTER('GA Посещения сайта';
RELATED('SHD Параметры местоположений'[Страна]) = "Russia");
'SHD Параметры местоположений'[Регион];
"Sessions";
SUM('GA Посещения сайта'[Сессии]));
NOT('SHD Параметры местоположений'[Регион] in {""; BLANK()}));
ALL('Карта_РФ_таблица'))
var ci_Ses = /* в третьей переменной рассчитываем верхнюю границу
доверительного интервала*/
AVERAGEX(All_table_sessions; [Sessions]) + /* выводим среднее и
прибавляем к нему значение доверительного интервала*/
CONFIDENCE.T(
0,01; /* задаем значение альфа, для 99% доверительного интервала
оно равно 0,01 */
STDEVX.S(All_table_sessions; [Sessions]); /* считаем стандартное
отклонение */
COUNTAX(All_table_sessions; 'SHD Параметры местоположений'[Регион])
/* указываем размер выборки */)
return
/* наконец, когда все нужные показатели рассчитаны, производим "подмену" */
IF(
MAXX(Table_sessions;[Sessions]) > ci_Ses;
ci_Ses;
MAXX(Table_sessions;[Sessions]))
/* для каждого региона выполняем проверку и если количество посещений
больше, чем верхняя граница доверительного интервала, то выводим верхнюю
границу, иначе оставляем реальное значение */Наша мера готова. Добавим ее на карту и посмотрим, что получилось.
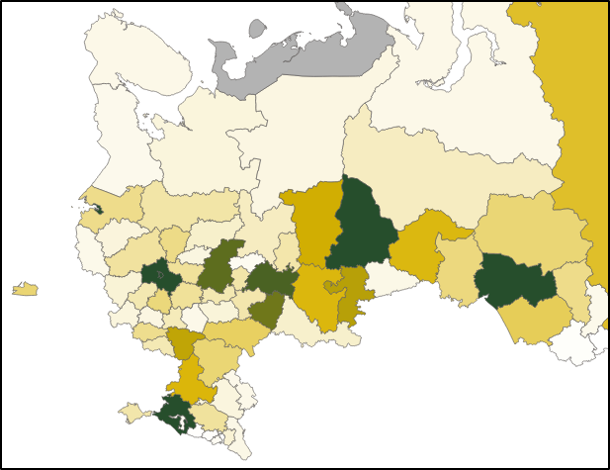

Добавим во всплывающую подсказку название региона, реальное количество посещений и значение нашей меры, которое назовем "Максимум / 99%".
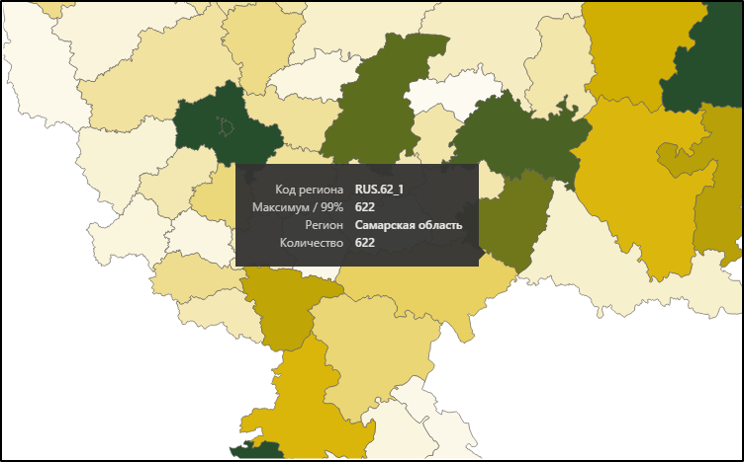
Выбрав Самарскую область, мы видим, что реальное количество посещений совпадает со значением нашей меры, а значит, оно не превышает верхнюю границу доверительного интервала.
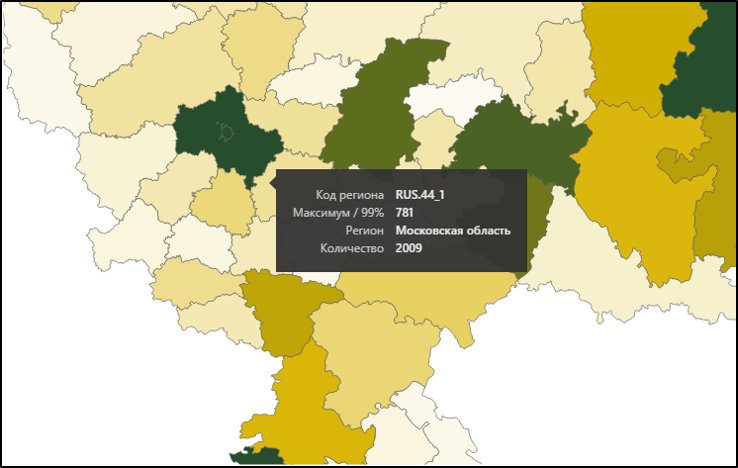
Но если мы выберем Московскую область, то увидим, что значения отличаются, что и является следствием нашей "подмены".
Результат нас устроил, однако, он мог бы быть немного другим. Дело в том, что существует еще один метод определения границ статистически значимой выборки. Он используется при построении диаграммы размаха, или "ящика с усами". Для определения верхней границы, при использовании этого метода, к медиане прибавляется значение межквартильного размаха, умноженное на определенный коэффициент. Чтобы использовать этот расчет в нашей мере, нужно вместо переменной ci_Ses вставить следующий код:
var top_limit =
MEDIANX(
All_table_sessions;
[Sessions]) + /* рассчитаем медиану */
((PERCENTILEX.EXC(
All_table_sessions;
[Sessions]; 0,75) - /* рассчитаем межквартильный интервал,
для этого из третьего квартиля вычтем первый */
PERCENTILEX.EXC(
All_table_sessions;
[Sessions]; 0,25)) * 3) /* и умножим его на нужный коэффициент */В нашем случае подошел коэффициент 3, хотя чаще используется 1,5. По сути, мы сами решаем, какой размах значений будет наилучшим образом описывать нашу выборку. Это удобно при тонкой настройке отображения визуализации, но может привести к непредсказуемому результату со временем, когда выборка будет меняться. Поэтому, мы сделали выбор в пользу автоматизации и оставили первый вариант.
Исход битвы
Итак, путем несложных манипуляций, нам удалось добиться красивой и информативной визуализации данных. Это особенно важно при использовании shape map, так как сам принцип отображения информации на такой карте, основывается на механизме условного форматирования. Естественно, я ни в коем случае не призываю фальсифицировать данные в угоду эстетической составляющей. Все описанные выше манипуляции возможны только при условии информирования пользователей и наличии доступа к реальным, неизмененным данным. Надеюсь, что статья будет полезна всем data-аналитикам, использующим в своей работе Power BI. Кстати, предложенное решение можно легко перенести в Эксель, где тоже встречается описанная проблема. Буду рад вашим замечаниям и комментариям.
P.S. Целью статьи не был разбор методов математической статистики, поэтому статистические термины в ней истолкованы достаточно вольно. Для изучения этих терминов рекомендую воспользоваться специальной литературой ;)





