Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В предыдущей статье мы определяли цвет одежды по изображению, и это может помочь нам для принятия решений о том, одежду каких стилей покупать, и каким клиентам их отправлять. Мы описали гибридный подход с участием человека и машины, однако подробно описывали только часть работы человека – перевод изображений в иерархию цветов. В данной статье мы углубимся в часть работы компьютера – наш текущий алгоритм компьютерного зрения, процесс его разработки и идеи на будущее.
Перед разработкой алгоритма нужно задуматься над тем, как мы будем оценивать его работу. Допустим, мы написали алгоритм, и он говорит, что «на этом изображении есть следующие цвета» – правильным ли будет его решение? И что это вообще значит — «правильным»?
Для решения этой задачи мы выбрали два важных измерения – правильную разметку основного цвета и правильное количество цветов. Мы задаём это как расстояние CIEDE 2000 (формула цветового отличия) между основным цветом, предсказанным нашим алгоритмом, и нашим реальным основным цветом, а также считаем среднюю абсолютную ошибку в количестве цветов. Такой выбор мы сделали по следующим соображениям:
Что насчёт «реальных» данных? Наша команда мерчандайзеров обеспечила нас метками, однако наши инструменты дают им возможность выбирать только самые общие цвета, вроде «серого» или «синего» – их нельзя назвать точным значением. Такие общие определения включают довольно много разнообразных оттенков, поэтому их в качестве реальных цветов использовать не получится. Придётся строить собственный набор данных.
Кто-то из вас мог уже задуматься о сервисах типа Mechanical Turk. Но нам не нужно размечать очень много изображений, поэтому описать эту задачу, возможно, будет даже тяжелее, чем просто выполнить её. Кроме того, создание набора данных помогает лучше разобраться в них. Мы по-быстрому сварганили приложение на HTML/Javascript и случайным образом выбрали 1000 изображений, выбрали для каждого пиксель, представляющий его основной цвет, и разметили количество увиденных нами на изображении цветов. После этого получить два числа, оценивающие качество нашего алгоритма, стало просто (расстояние до главного цвета CIEDE и количество цветов MAE).
Иногда мы проверяли работу программ вручную, запуская оба алгоритма на одном изображении и выводя два списка цветов. Затем мы вручную проставили оценки 200 изображениям, выбирая, какие цвета были распознаны «лучше». Очень важно подобным образом плотно работать с данными – чтобы не просто получить результат («алгоритм Б в 70% случаев отработал лучше алгоритма А»), но и понять, что происходит в каждом из случаев («алгоритм Б обычно выбирает слишком много групп, а алгоритм А упускает светлые цвета»).

Свитер и выбранные двумя разными алгоритмами цвета
Перед обработкой изображений мы преобразуем их в цветовое пространство CIELAB (или просто LAB) вместо более распространённого RGB. В результате наши три цифры будут обозначать не количество красного, зелёного и синего. Точки пространства LAB (правильнее будет L*a*b*, но мы для простоты будем писать LAB) обозначают три разных оси. L обозначает яркость от чёрного 0 до белого 100. A и B обозначают цвет: А указывает место в диапазоне от зелёного -128 до красного 127, а В – от синего -128 до жёлтого 127. Основное преимущество такого пространства – воспринимаемая однородность. Расстояние или разница между двумя точками в пространстве LAB будет восприниматься одинаково, вне зависимости от их местонахождения, если евклидово расстояние между ними в пространстве тоже будет одинаковым.
Естественно, у LAB есть другие проблемы: к примеру, мы рассматриваем изображения на компьютерных экранах, использующих RGB-пространство, зависящее от устройства. Также гамма LAB шире, чем у RGB, то есть в LAB можно выражать такие цвета, какие не выразишь через RGB. Поэтому преобразование из LAB в RGB не может быть двусторонним – преобразовав точку в одном направлении, а потом в обратном, можно получить другое значение. Теоретически эти недочёты присутствуют, но на практике метод всё равно работает.
Преобразовав картинку в LAB, мы получим набор пикселей, которые можно рассматривать, как точки (L, A, B, X, Y). Оставшаяся часть алгоритма занимается группировкой этих точек, при которой группы первого этапа используют все пять измерений, а второго – опускают измерения X и Y.
Мы начинаем с изображения без группировки пикселей, прошедшего цветовую корректировку, описанную в предыдущей статье, сжатого до 320×200 и преобразованного в LAB.

Для начала применим алгоритм Quickshift, группирующий близлежащие пиксели в «суперпиксели».

Это уже сводит наше изображение, содержащее 60 000 пикселей, к нескольким сотням суперпикселей, удаляя ненужную сложность. Ещё более упростить ситуацию можно, слив воедино близлежащие суперпиксели с небольшим цветовым расстоянием между ними. Для этого мы рисуем их граф региональной близости – граф, в котором обозначающие два разных суперпикселя узлы соединяются ребром, если их пиксели соприкасаются.

Слева – граф региональной близости (Regional Adjacency Graph, RAG) для кардигана. Тёмные линии, соединяющие суперпиксели, говорят о том, что между ними нет особой цветовой разницы, и поэтому их можно сливать. Яркие линии, или их отсутствие, говорят о высоком различии между цветами, и о том, что их сливать не надо. Справа – суперпиксели, слитые после обработки графа по пороговым значениям.
Узлы графа – вычисленные нами суперпиксели, а рёбра – расстояние между ними в цветовом пространстве. У ребра, соединяющего два близлежащих суперпикселя с похожими цветами будет низкий вес (тёмные линии), а у ребра между суперпикселями с очень разными цветами – высокий (яркие линии, а также отсутствие линий – их не рисовали, если их вес больше 20). Существует много способов скомбинировать близлежащие суперпиксели, однако для нас оказалось достаточно простого порогового значения, равного 10.
В нашем случае 60 000 пикселей получилось свести к 100 участкам, в каждом из которых содержатся пиксели одного цвета. Это даёт преимущества при вычислениях: во-первых, мы знаем, что большой суперпиксель почти белого цвета – это фон, и его можно удалить. Мы удаляем все суперпиксели, у которых L>99, а А и В находятся в промежутке от -0,5 до 0,5. Во-вторых, мы можем сильно уменьшить количество пикселей на следующем шаге. У нас не получится уменьшить их количество до 100, поскольку нам надо взвешивать участки на основании количества содержащихся в них пикселей. Но мы можем легко удалить 90% пикселей из каждой группы, не особенно потеряв в детализации и почти не исказив следующей группировки.
На данном шаге у нас есть несколько тысяч пикселей с координатами (L, A, B). Существует множество методов, способных красиво сгруппировать эти пиксели. Мы выбрали метод k-средних, поскольку он быстро работает, прост для понимания, у наших данных есть только 3 измерения, и евклидовое расстояние в LAB-пространстве имеет смысл.
Мы не особо умничали и провели группировку с К=8. Если в какой-то группе содержится меньше 3% точек, мы пробуем снова, уже с К=7, потом 6, и так далее. В итоге мы имеем список от 1 до 8 центров группировки и доли количества точек, принадлежащих к каждому из центров. Названия им даёт алгоритм colornamer, описанный в предыдущей статье.
Мы достигли среднего расстояния в 5,86 по шкале CIEDE 2000 между предсказанным и «реальным» цветом. Правильно интерпретировать этот показатель довольно сложно. По простой метрике расстояния CIE76 наша средняя дистанция равняется 7,82. По этой метрике значение 2,3 означает едва различимую разницу. Поэтому можно сказать, что наши результаты, немного превышающие 3, обозначают едва заметную разницу.
Также наш показатель MAE составил 2,28 цветов. Но опять-таки, это вторичная метрика. Многие описанные далее алгоритмы уменьшают эту ошибку, но за счёт увеличения цветового расстояния. Гораздо проще проигнорировать ложные цвета, стоящие на 5-м или 6-м месте, чем проигнорировать неправильный 1-й цвет.

Даже вещи явно одного цвета, как эти шорты, содержат области, из-за теней кажущиеся гораздо более тёмными
Остаётся проблема теней. Ткань не уложишь идеально ровно, поэтому часть изображения всегда останется в тени, и будет казаться обманчиво другого цвета. Простейшие подходы вроде поиска дубликатов цветов одного оттенка и разной яркости не работают, поскольку переход от «пикселя без тени» к «пикселю в тени» не всегда работает одинаково. В будущем мы надеемся использовать более хитрые техники вроде DeshadowNet или автоматического распознавания теней.

Мы сконцентрировались только на цвете одежды. У бижутерии и туфель свои проблемы: наши фотографии украшений слишком маленькие, а на фотографиях обуви часто видно её внутренность. В приведённом выше примере мы бы указали наличие на фото бургундского и охры, хотя важен только первый из них.
Этот последний алгоритм кажется довольно простым, но до него непросто было додуматься! В данном разделе я опишу варианты, которые мы пробовали и на которых учились.
Мы пробовали алгоритмы удаления фона – к примеру, алгоритм от Lyst. Неформальная оценка показала, что они работают не так точно, как простое удаление белого фона. Однако мы планируем поглубже изучить его по мере обработки изображений, над которыми не работала наша фотостудия.
Некоторые библиотеки для извлечения цветов выбрали простое решение данной задачи: группировать пиксели, хэшируя их в несколько достаточно широких контейнеров, а потом возвращать средние значения LAB контейнеров с наибольшим количеством пикселей. Мы опробовали библиотеку Colorgram.py; несмотря на её простоту, работает она удивительно неплохо. Кроме того, она работает быстро – не более секунды на изображение, в то время, как наш алгоритм тратит десятки секунд на одно изображение. Однако среднее расстояние до основного цвета у Colorgram.py было больше, чем у нашего алгоритма – в основном потому, что его результат взят у средних расстояний до больших контейнеров. Тем не менее, мы иногда используем его для случаев, когда скорость важнее точности.
Мы используем алгоритм Quickshift для сегментирования изображения на суперпиксели, однако возможных алгоритмов существует несколько – к примеру, SLIC, Watershed и Felzenszwalb. На практике лучшие результаты показал Quickshift благодаря его работе с мелкими деталями. К примеру, у SLIC есть проблема с такими вещами, как полоски, занимающие много места на картинке. Вот показательные результаты работы алгоритма SLIC с разными настройками:

Оригинальное изображение

compactness=1

compactness=10

compactness=100
Для работы с нашими данными у Quickshift есть одно теоретическое преимущество: он не требует непрерывной связи суперпикселей. Исследователи отмечали, что из-за этого у алгоритмов могут возникать проблемы, однако в нашем случае это преимущество – часто у нас попадаются небольшие области с мелкими деталями, которые мы хотим привести к одной группе.

Рубашка в клеточку

Её суперпиксельная группировка от Quickshift
Хотя суперпиксельная группировка от Quickshift выглядит хаотично, на самом деле она группирует все красные полоски с другими красными, синие с синими, и т.п.
При использовании метода k-средних чаще всего возникает вопрос: каким сделать «k»? То есть, если нам надо группировать точки в некоторое количество групп, сколько их нужно делать? Для ответа на вопрос было разработано несколько подходов. Простейший – «локтевой метод», однако он требует ручной обработки графа, а нам нужно автоматическое решение. Статистика разрывов [Gap Statistic] формализует этот метод, и с её помощью мы получили лучшие результаты по метрике «количества цветов», однако за счёт точности определения основного цвета. Поскольку основной цвет важнее всего, мы не использовали её в рабочей программе, но планируем далее изучать этот вопрос.
Наконец, метод силуэта – ещё один популярный метод выбора k. Он выдаёт резульатты чуть хуже, чем наш алгоритм, и у него есть один серьёзный недостаток: ему нужно не менее 2 групп. Но у многих артикулов одежды есть только один цвет.
Одно потенциальное решение вопроса выбора k – использовать алгоритм, не требующий от вас выбирать этот параметр. Один из популярных примеров – DBSCAN, ищущий в данных группы примерно равной плотности.

Разноцветная блузка
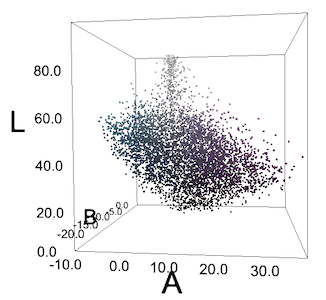
Все пиксели её изображения в LAB-пространстве. Пиксели не формируют чётких групп «зеленовато-голубой» и «фиолетовый».
Часто у нас не получается таких групп, или мы видим что-то наподобие групп только из-за особенностей человеческого восприятия. Для нас зеленовато-голубые «огурцы» на блузке выделяются на фиолетовом фоне, но если мы построим все пиксели в координатах RGB или LAB, они не сформируют групп. Но мы всё равно пробовали DBSCAN с различными значениями эпсилон – и получили предсказуемо неважные результаты.
Один из хороших принципов исследователи – посмотреть, не решил ли кто уже вашу проблему. Лео Эрколанелли с сайта Algolia опубликовал подробное описание решения такой задачи более трёх лет назад. Благодаря их щедрости в раздаче исходников, мы смогли сами попробовать их решение. Однако результаты получились чуть хуже наших, поэтому мы оставили наш алгоритм. Они решают не совсем ту же проблему, что мы: у них были изображения товаров на моделях и на отличном от белого фоне, поэтому разумно, что их результаты отличаются от наших.
Этот алгоритм завершает процесс, описанный в нашей предыдущей статье. После извлечения центров групп мы используем Colornamer для назначения им имён, а потом импортируем эти цвета в наши внутренние инструменты. Это помогает нам легко визуализировать нашу продукцию по цветам; мы надеемся включить эти данные в алгоритмы рекомендаций покупок. Этот процесс нельзя назвать идеальным решением, он помогает нам получить лучшие данные о тысячах наших товаров, что, в свою очередь, способствует нашей главной цели: помогать людям находить стили, которые им понравятся.
Опрос о переводе первой части
Откуда нам знать, что алгоритм работает?
Перед разработкой алгоритма нужно задуматься над тем, как мы будем оценивать его работу. Допустим, мы написали алгоритм, и он говорит, что «на этом изображении есть следующие цвета» – правильным ли будет его решение? И что это вообще значит — «правильным»?
Для решения этой задачи мы выбрали два важных измерения – правильную разметку основного цвета и правильное количество цветов. Мы задаём это как расстояние CIEDE 2000 (формула цветового отличия) между основным цветом, предсказанным нашим алгоритмом, и нашим реальным основным цветом, а также считаем среднюю абсолютную ошибку в количестве цветов. Такой выбор мы сделали по следующим соображениям:
- Эти параметры легко подсчитать.
- При увеличении количества метрик было бы труднее выбрать «лучший» алгоритм.
- При уменьшении количества метрик мы можем упустить важное различие между двумя алгоритмами.
- В любом случае у большинства предметов одежды есть один-два главных цвета, и многие из наших процессов полагаются на основной цвет. Поэтому правильно вычислить основной цвет гораздо важнее, чем правильно вычислить второй или третий цвета.
Что насчёт «реальных» данных? Наша команда мерчандайзеров обеспечила нас метками, однако наши инструменты дают им возможность выбирать только самые общие цвета, вроде «серого» или «синего» – их нельзя назвать точным значением. Такие общие определения включают довольно много разнообразных оттенков, поэтому их в качестве реальных цветов использовать не получится. Придётся строить собственный набор данных.
Кто-то из вас мог уже задуматься о сервисах типа Mechanical Turk. Но нам не нужно размечать очень много изображений, поэтому описать эту задачу, возможно, будет даже тяжелее, чем просто выполнить её. Кроме того, создание набора данных помогает лучше разобраться в них. Мы по-быстрому сварганили приложение на HTML/Javascript и случайным образом выбрали 1000 изображений, выбрали для каждого пиксель, представляющий его основной цвет, и разметили количество увиденных нами на изображении цветов. После этого получить два числа, оценивающие качество нашего алгоритма, стало просто (расстояние до главного цвета CIEDE и количество цветов MAE).
Иногда мы проверяли работу программ вручную, запуская оба алгоритма на одном изображении и выводя два списка цветов. Затем мы вручную проставили оценки 200 изображениям, выбирая, какие цвета были распознаны «лучше». Очень важно подобным образом плотно работать с данными – чтобы не просто получить результат («алгоритм Б в 70% случаев отработал лучше алгоритма А»), но и понять, что происходит в каждом из случаев («алгоритм Б обычно выбирает слишком много групп, а алгоритм А упускает светлые цвета»).

Свитер и выбранные двумя разными алгоритмами цвета
Наш алгоритм извлечения цвета
Перед обработкой изображений мы преобразуем их в цветовое пространство CIELAB (или просто LAB) вместо более распространённого RGB. В результате наши три цифры будут обозначать не количество красного, зелёного и синего. Точки пространства LAB (правильнее будет L*a*b*, но мы для простоты будем писать LAB) обозначают три разных оси. L обозначает яркость от чёрного 0 до белого 100. A и B обозначают цвет: А указывает место в диапазоне от зелёного -128 до красного 127, а В – от синего -128 до жёлтого 127. Основное преимущество такого пространства – воспринимаемая однородность. Расстояние или разница между двумя точками в пространстве LAB будет восприниматься одинаково, вне зависимости от их местонахождения, если евклидово расстояние между ними в пространстве тоже будет одинаковым.
Естественно, у LAB есть другие проблемы: к примеру, мы рассматриваем изображения на компьютерных экранах, использующих RGB-пространство, зависящее от устройства. Также гамма LAB шире, чем у RGB, то есть в LAB можно выражать такие цвета, какие не выразишь через RGB. Поэтому преобразование из LAB в RGB не может быть двусторонним – преобразовав точку в одном направлении, а потом в обратном, можно получить другое значение. Теоретически эти недочёты присутствуют, но на практике метод всё равно работает.
Преобразовав картинку в LAB, мы получим набор пикселей, которые можно рассматривать, как точки (L, A, B, X, Y). Оставшаяся часть алгоритма занимается группировкой этих точек, при которой группы первого этапа используют все пять измерений, а второго – опускают измерения X и Y.
Группировка в пространстве
Мы начинаем с изображения без группировки пикселей, прошедшего цветовую корректировку, описанную в предыдущей статье, сжатого до 320×200 и преобразованного в LAB.

Для начала применим алгоритм Quickshift, группирующий близлежащие пиксели в «суперпиксели».

Это уже сводит наше изображение, содержащее 60 000 пикселей, к нескольким сотням суперпикселей, удаляя ненужную сложность. Ещё более упростить ситуацию можно, слив воедино близлежащие суперпиксели с небольшим цветовым расстоянием между ними. Для этого мы рисуем их граф региональной близости – граф, в котором обозначающие два разных суперпикселя узлы соединяются ребром, если их пиксели соприкасаются.

Слева – граф региональной близости (Regional Adjacency Graph, RAG) для кардигана. Тёмные линии, соединяющие суперпиксели, говорят о том, что между ними нет особой цветовой разницы, и поэтому их можно сливать. Яркие линии, или их отсутствие, говорят о высоком различии между цветами, и о том, что их сливать не надо. Справа – суперпиксели, слитые после обработки графа по пороговым значениям.
Узлы графа – вычисленные нами суперпиксели, а рёбра – расстояние между ними в цветовом пространстве. У ребра, соединяющего два близлежащих суперпикселя с похожими цветами будет низкий вес (тёмные линии), а у ребра между суперпикселями с очень разными цветами – высокий (яркие линии, а также отсутствие линий – их не рисовали, если их вес больше 20). Существует много способов скомбинировать близлежащие суперпиксели, однако для нас оказалось достаточно простого порогового значения, равного 10.
В нашем случае 60 000 пикселей получилось свести к 100 участкам, в каждом из которых содержатся пиксели одного цвета. Это даёт преимущества при вычислениях: во-первых, мы знаем, что большой суперпиксель почти белого цвета – это фон, и его можно удалить. Мы удаляем все суперпиксели, у которых L>99, а А и В находятся в промежутке от -0,5 до 0,5. Во-вторых, мы можем сильно уменьшить количество пикселей на следующем шаге. У нас не получится уменьшить их количество до 100, поскольку нам надо взвешивать участки на основании количества содержащихся в них пикселей. Но мы можем легко удалить 90% пикселей из каждой группы, не особенно потеряв в детализации и почти не исказив следующей группировки.
Группировка без использования пространства
На данном шаге у нас есть несколько тысяч пикселей с координатами (L, A, B). Существует множество методов, способных красиво сгруппировать эти пиксели. Мы выбрали метод k-средних, поскольку он быстро работает, прост для понимания, у наших данных есть только 3 измерения, и евклидовое расстояние в LAB-пространстве имеет смысл.
Мы не особо умничали и провели группировку с К=8. Если в какой-то группе содержится меньше 3% точек, мы пробуем снова, уже с К=7, потом 6, и так далее. В итоге мы имеем список от 1 до 8 центров группировки и доли количества точек, принадлежащих к каждому из центров. Названия им даёт алгоритм colornamer, описанный в предыдущей статье.
Результаты и оставшиеся проблемы
Мы достигли среднего расстояния в 5,86 по шкале CIEDE 2000 между предсказанным и «реальным» цветом. Правильно интерпретировать этот показатель довольно сложно. По простой метрике расстояния CIE76 наша средняя дистанция равняется 7,82. По этой метрике значение 2,3 означает едва различимую разницу. Поэтому можно сказать, что наши результаты, немного превышающие 3, обозначают едва заметную разницу.
Также наш показатель MAE составил 2,28 цветов. Но опять-таки, это вторичная метрика. Многие описанные далее алгоритмы уменьшают эту ошибку, но за счёт увеличения цветового расстояния. Гораздо проще проигнорировать ложные цвета, стоящие на 5-м или 6-м месте, чем проигнорировать неправильный 1-й цвет.

Даже вещи явно одного цвета, как эти шорты, содержат области, из-за теней кажущиеся гораздо более тёмными
Остаётся проблема теней. Ткань не уложишь идеально ровно, поэтому часть изображения всегда останется в тени, и будет казаться обманчиво другого цвета. Простейшие подходы вроде поиска дубликатов цветов одного оттенка и разной яркости не работают, поскольку переход от «пикселя без тени» к «пикселю в тени» не всегда работает одинаково. В будущем мы надеемся использовать более хитрые техники вроде DeshadowNet или автоматического распознавания теней.

Мы сконцентрировались только на цвете одежды. У бижутерии и туфель свои проблемы: наши фотографии украшений слишком маленькие, а на фотографиях обуви часто видно её внутренность. В приведённом выше примере мы бы указали наличие на фото бургундского и охры, хотя важен только первый из них.
Что ещё мы пробовали
Этот последний алгоритм кажется довольно простым, но до него непросто было додуматься! В данном разделе я опишу варианты, которые мы пробовали и на которых учились.
Удаление фона
Мы пробовали алгоритмы удаления фона – к примеру, алгоритм от Lyst. Неформальная оценка показала, что они работают не так точно, как простое удаление белого фона. Однако мы планируем поглубже изучить его по мере обработки изображений, над которыми не работала наша фотостудия.
Хэширование пикселей
Некоторые библиотеки для извлечения цветов выбрали простое решение данной задачи: группировать пиксели, хэшируя их в несколько достаточно широких контейнеров, а потом возвращать средние значения LAB контейнеров с наибольшим количеством пикселей. Мы опробовали библиотеку Colorgram.py; несмотря на её простоту, работает она удивительно неплохо. Кроме того, она работает быстро – не более секунды на изображение, в то время, как наш алгоритм тратит десятки секунд на одно изображение. Однако среднее расстояние до основного цвета у Colorgram.py было больше, чем у нашего алгоритма – в основном потому, что его результат взят у средних расстояний до больших контейнеров. Тем не менее, мы иногда используем его для случаев, когда скорость важнее точности.
Другой алгоритм разделения на суперпиксели
Мы используем алгоритм Quickshift для сегментирования изображения на суперпиксели, однако возможных алгоритмов существует несколько – к примеру, SLIC, Watershed и Felzenszwalb. На практике лучшие результаты показал Quickshift благодаря его работе с мелкими деталями. К примеру, у SLIC есть проблема с такими вещами, как полоски, занимающие много места на картинке. Вот показательные результаты работы алгоритма SLIC с разными настройками:

Оригинальное изображение

compactness=1

compactness=10

compactness=100
Для работы с нашими данными у Quickshift есть одно теоретическое преимущество: он не требует непрерывной связи суперпикселей. Исследователи отмечали, что из-за этого у алгоритмов могут возникать проблемы, однако в нашем случае это преимущество – часто у нас попадаются небольшие области с мелкими деталями, которые мы хотим привести к одной группе.

Рубашка в клеточку

Её суперпиксельная группировка от Quickshift
Хотя суперпиксельная группировка от Quickshift выглядит хаотично, на самом деле она группирует все красные полоски с другими красными, синие с синими, и т.п.
Разные методы подсчёта количества групп
При использовании метода k-средних чаще всего возникает вопрос: каким сделать «k»? То есть, если нам надо группировать точки в некоторое количество групп, сколько их нужно делать? Для ответа на вопрос было разработано несколько подходов. Простейший – «локтевой метод», однако он требует ручной обработки графа, а нам нужно автоматическое решение. Статистика разрывов [Gap Statistic] формализует этот метод, и с её помощью мы получили лучшие результаты по метрике «количества цветов», однако за счёт точности определения основного цвета. Поскольку основной цвет важнее всего, мы не использовали её в рабочей программе, но планируем далее изучать этот вопрос.
Наконец, метод силуэта – ещё один популярный метод выбора k. Он выдаёт резульатты чуть хуже, чем наш алгоритм, и у него есть один серьёзный недостаток: ему нужно не менее 2 групп. Но у многих артикулов одежды есть только один цвет.
DBSCAN
Одно потенциальное решение вопроса выбора k – использовать алгоритм, не требующий от вас выбирать этот параметр. Один из популярных примеров – DBSCAN, ищущий в данных группы примерно равной плотности.

Разноцветная блузка

Все пиксели её изображения в LAB-пространстве. Пиксели не формируют чётких групп «зеленовато-голубой» и «фиолетовый».
Часто у нас не получается таких групп, или мы видим что-то наподобие групп только из-за особенностей человеческого восприятия. Для нас зеленовато-голубые «огурцы» на блузке выделяются на фиолетовом фоне, но если мы построим все пиксели в координатах RGB или LAB, они не сформируют групп. Но мы всё равно пробовали DBSCAN с различными значениями эпсилон – и получили предсказуемо неважные результаты.
Решение от Algolia
Один из хороших принципов исследователи – посмотреть, не решил ли кто уже вашу проблему. Лео Эрколанелли с сайта Algolia опубликовал подробное описание решения такой задачи более трёх лет назад. Благодаря их щедрости в раздаче исходников, мы смогли сами попробовать их решение. Однако результаты получились чуть хуже наших, поэтому мы оставили наш алгоритм. Они решают не совсем ту же проблему, что мы: у них были изображения товаров на моделях и на отличном от белого фоне, поэтому разумно, что их результаты отличаются от наших.
Координация цветов
Этот алгоритм завершает процесс, описанный в нашей предыдущей статье. После извлечения центров групп мы используем Colornamer для назначения им имён, а потом импортируем эти цвета в наши внутренние инструменты. Это помогает нам легко визуализировать нашу продукцию по цветам; мы надеемся включить эти данные в алгоритмы рекомендаций покупок. Этот процесс нельзя назвать идеальным решением, он помогает нам получить лучшие данные о тысячах наших товаров, что, в свою очередь, способствует нашей главной цели: помогать людям находить стили, которые им понравятся.
Опрос о переводе первой части
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Нужно ли переводить предыдущую статью про базовые понятия из области восприятия цветов?
-
100,0%Давайте10
-
0,0%Не надо0





