Введение
В первой части этой серии статей мы рассмотрим теоретическую сторону дизеринга, немного истории и применение его к 1D-сигналам и дискретизации. Я попытаюсь провести частотный анализ ошибок дискретизации и расскажу о том, как дизеринг помогает их исправить. В основном это будет теоретическая статья, поэтому если вам интересны более практические применения, то ждите следующих частей.
Блокнот Mathematica для воспроизведения результатов можно найти здесь, а pdf-версия находится здесь.
Что такое дизеринг?
Дизеринг (Dithering) можно описать как намеренное/осознанное внесение в сигнал шума для предотвращения ошибок большого масштаба/низкого разрешения, возникающих вследствие дискретизации или субдискретизации.
Если вы когда-нибудь работали с:
- Аудиосигналами,
- Палитровыми форматами изображений 90-х
то должны были встречать опции дизеринга, которые благодаря добавлению шума и артефактов низкого разрешения «магически» улучшали качество звука или изображений.
Однако я обнаружил в Википедии довольно удивительный факт о том, как впервые был определён и использован дизеринг:
…Одна из первых областей применения дизеринга возникла во время Второй мировой войны. Самолёты-бомбардировщики для навигации и вычислений траектории бомб использовали механические компьютеры. Любопытно, что эти компьютеры (ящики, заполненные сотнями шестерёнок и зубчатых передач) работали точнее при полёте на борту самолёта, чем на земле. Инженеры поняли, что вызываемая самолётом вибрация снижает ошибку, вызываемую липкими подвижными деталями. На земле они двигались короткими отрывистыми движениями, а в воздухе их движение было более непрерывным. В компьютеры встроили небольшие вибромоторчики, и их вибрацию назвали «дизером» (dither), от среднеанглийского слова «didderen», означающего «дрожать». Сегодня, когда вы стучите по механическому измерителю, чтобы повысить его точность, вы применяете dither. При использовании в небольших количествах dither успешно превращает систему оцифровки в более аналоговую, в хорошем смысле этого слова.
— Кен Полманн, Principles of Digital Audio
Это вдохновляющий и интересный исторический факт и мне понятно, почему он позволяет избегать отклонений в вычислениях и резонансах, случайным образом разрушая циклы обратной связи механической вибрации.
Но хватит истории, давайте для начала рассмотрим процесс дизеринга в 1D-сигналах, например, в аудио.
Дискретизация дизерингом постоянного сигнала
Мы начнём с анализа самого скучного в мире сигнала — постоянного сигнала. Если вы знаете немного о цифровой обработке сигналов, связанных со звуком, то можете сказать: но ты же обещал рассмотреть аудио, а в звуке по определению нет постоянной составляющей! (Более того, и в ПО, и в оборудовании обработки звука намеренно устраняется так называемый сдвиг постоянной составляющей (DC offset).)
Это правда, и вскоре мы рассмотрим более сложные функции, но начнём мы сначала.
Представьте, что мы выполняем 1-битную дискретизацию нормализованного сигнала с плавающей запятой. Это значит, что мы имеем дело только с конечными двоичными значениями, 0 или 1.
Если сигнал равен 0,3, то простое округление без дизеринга будет самой скучной функцией — просто нулём!
Погрешность тоже постоянна и равна 0,3, следовательно, и средняя погрешность равна 0,3. Это означает, что мы внесли довольно большое отклонение в сигнал и полностью потеряли информацию исходного сигнала.
Мы можем попробовать выполнить дизеринг этого сигнала и посмотреть на результаты.
Дизеринг в этом случае (при использовании функции округления) просто применяет обычный случайный белый шум (случайное значение для каждого элемента, что создаёт равномерный спектр шума) и прибавляет в сигнал перед дискретизацией случайное в интервале (-0.5, 0.5).
quantizedDitheredSignal =
Round[constantSignalValue + RandomReal[] – 0.5] & /@ Range[sampleCount];


Здесь сложно что-то увидеть, теперь результат дискретизации — это просто набор случайных единиц и нулей. С (ожидаемо) большим количеством нулей. Сам по себе этот сигнал не особо интересен, однако довольно интересен график погрешностей и средняя погрешность.

Итак, как мы и ожидали, погрешность тоже варьируется, но пугает то, что погрешность иногда стала больше (абсолютное значение 0,7)! То есть максимальная погрешность к сожалению стала хуже, однако средний шум имеет значение:
Mean[ditheredSignalError]
0.013
Намного лучше, чем первоначальная погрешность в 0,3. При значительно большом количестве сэмплов эта погрешность будет стремиться к нулю (к пределу). Итак, погрешность постоянной составляющей стала намного меньше, но давайте взглянем на частотный график всех погрешностей.
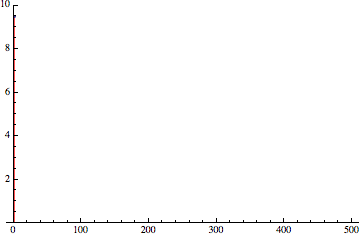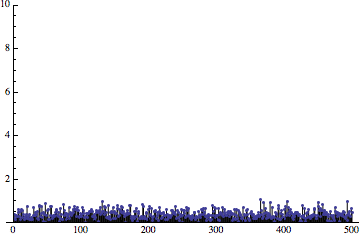
Красный график/всплеск = частотный спектр погрешности при отсутствии дизеринга (постоянный сигнал без частот). Чёрный — с дизерингом при помощи белого шума.
Всё становится интереснее! Это демонстрирует первый вывод из этого поста — дизеринг распределяет погрешность/отклонение дискретизации среди множества частот.
В следующем разделе мы узнаем, как это нам поможет.
Частотная чувствительность и низкочастотная фильтрация
Выше мы наблюдали за дизерингом дискретизированного постоянного сигнала:
- Он увеличил максимальную погрешность.
- Почти обнулил среднюю погрешность.
- Добавил к спектру частот погрешностей постоянный белый шум (с полным покрытием спектра), снизив низкочастотную погрешность.
Сам по себе он нам не очень полезен… Однако мы рассматриваем не дискретизацию любой произвольной математической функции/сигнала. Мы рассматриваем сигналы, которые будут восприниматься человеком. Очевидно, что восприятие человека ограничено. Вот несколько примеров этого:
- Наше зрение имеет предел остроты. У многих людей есть близорукость и без очков они видят размытые изображения далёких объектов.
- Мы воспринимаем средний масштаб деталей гораздо лучше, чем очень высокие или очень низкие частоты (мелкие детали очень плавных градиентов могут быть незаметными).
- Наш слух работает в определённом диапазоне частот (20 Гц — 20 кГц, но со временем ухудшается) и наиболее чувствительны мы к среднему диапазону — 2 кГц — 5 кГц.
Следовательно, любая погрешность в частотах ближе к верхнему диапазону воспринимаемой частоты будет гораздо менее заметна.
Более того, наши медиаустройства становятся всё лучше и лучше, обеспечивая большую избыточную дискретизацию (oversampling). Например, в случае телевизоров и мониторов у нас есть технология «retina» и 4K-дисплеи (на которых невозможно разглядеть отдельный пиксель), в области звука мы используем форматы файлов с дискретизацией не менее 44 кГц даже для дешёвых динамиков, которые часто не могут воспроизводить больше, чем 5-10 кГц.
Это значит, что мы можем аппроксимировать воспринимаемый внешний вид сигнала, выполнив его низкочастотную фильтрацию. На графике я выполнил низкочастотную фильтрацию (заполнение нулями слева — это «нарастание»):
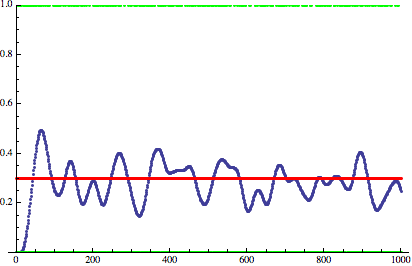
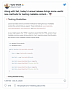
Красный — желаемый недискретизированный сигнал. Зелёный — дискретизированный сигнал с дизерингом. Синий — низкочастотный фильтр этого сигнала.
Сигнал начинает выглядеть гораздо более близким к исходной, недискретизированной функции!
К сожалению, мы начинаем видеть низкие частоты, которые очень заметны и отсутствуют в исходном сигнале. В третьей части серии мы попробуем исправить при помощи синего шума. А пока вот как график может выглядеть с функцией псевдо-шума, имеющей содержимое с гораздо меньшей частотой:

Но давайте закончим рассматривать простые, постоянные функции. Взглянем на синусоиду (если вы знакомы с теоремой Фурье, то знаете, что она является строительным блоком любого периодического сигнала!).
Дискретизация синусоиды
Если мы дискретизируем синусоиду 1-битной дискретизацией, то получим простой прямоугольный сигнал.

Прямоугольный сигнал довольно интересен, потому что включает в себя и базовую частоту, и нечётные гармоники.
Это интересное свойство, которое активно используется в аналоговых субтрактивных синтезаторах для создания звучания полых/медных инструментов. Субтрактивный синтез берёт сложный, гармонически богатый звук и фильтрует его, устраняя некоторые частоты (параметры фильтра варьируются со временем), чтобы придать звукам нужную форму.
Спектр частот прямоугольного сигнала:

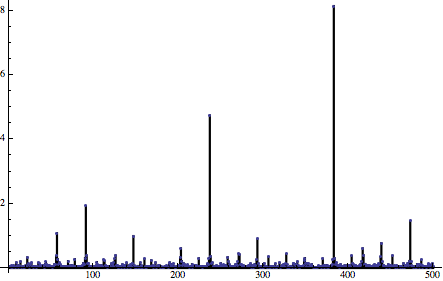
Но в этом посте нас больше интересую погрешности дискретизации! Давайте создадим график погрешности, а также спектр частот погрешности:

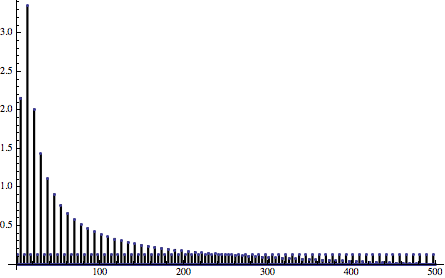
В этом случае ситуация гораздо лучше — средняя погрешность близка к нулю! К сожалению, у нас по-прежнему присутствует множество нежелательных низких частот, очень близких к нашей основной частоте (нечётных множителей с уменьшающейся величиной). Это явление называется алиасингом или шумом дизеринта — возникают частоты, отсутствовавшие в исходном сигнале, и они имеют довольно большие величины.
Даже низкочастотная фильтрация не сможет значительно помочь сигналу. Погрешность имеет очень много низких частот:
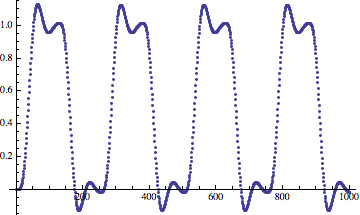
Дискретизированная синусоида с низкочастотной фильтрацией

Погрешность дискретизированной синусоиды с низкочастотной фильтрацией
Давайте взглянем, как меняется ситуация при добавлении дизеринга. На первый взгляд, улучшений почти нет:
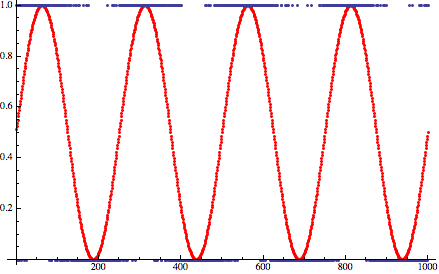
Однако если мы рассмотрим это как изображение, то оно начинает выглядеть лучше:

Заметьте, что погрешности дискретизации снова распределены среди различных частот:
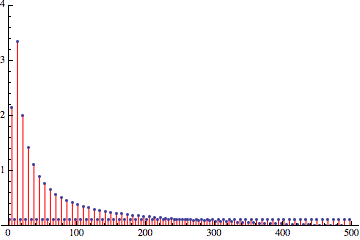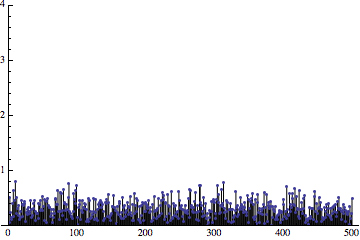
Выглядит очень многообещающе! Особенно учитывая то, что теперь мы можем попробовать выполнить фильтрацию:
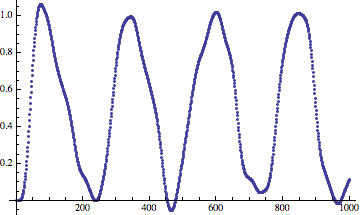
Это немного искажённая синусоида, но она выглядит намного ближе к исходной, чем версия без дизеринга, за исключением фазового сдвига, внесённого асимметричным фильтром (я не буду объяснять этого здесь; скажу только, что проблему можно устранить, применив симметричные фильтры):
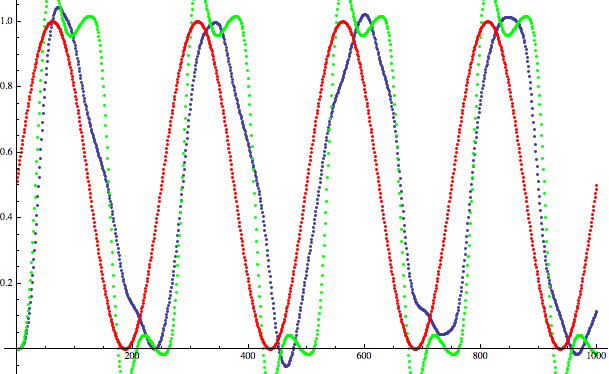
Красный — исходная синусоида. Зелёный — подвергнутый низкочастотной фильтрации сигнал без дизеринга. Синий — подвергнутый низкочастотной фильтрации сигнал с дизерингом.
Графики обеих погрешностей численно подтверждают, что погрешность намного меньше:

Красный — погрешность подвергнутого низкочастотной фильтрации сигнала без дизеринга. Синий — погрешность подвергнутого низкочастотной фильтрации сигнала с дизерингом.
Наконец, давайте вкратце рассмотрим сигнал с более качественной функцией дизеринга, содержащей только высокие частоты:

Верхнее изображение — функция белого шума. Нижнее изображение — функция, содержащая более высокие частоты.
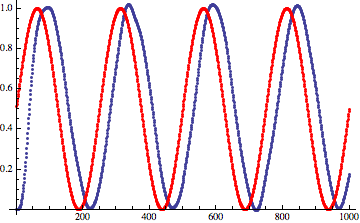
Версия с низкочастотной фильтрацией, дизерингом и улучшенной функцией — почти идеальные результаты, если не учитывать фазовый сдвиг, вызванный фильтром!
И наконец, сравнение всех трёх спектров погрешностей:
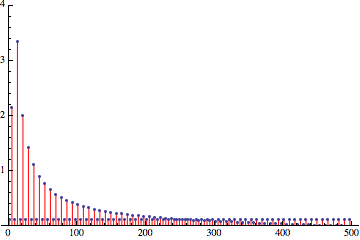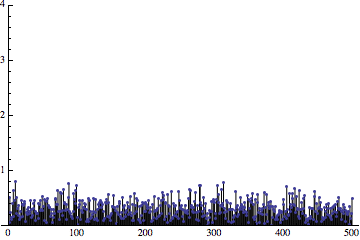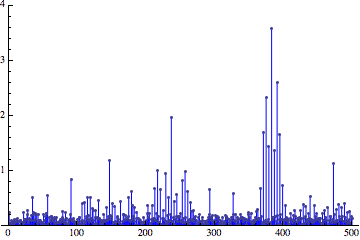
Красный — спектр погрешности дискретизации без дизеринга. Чёрный — спектр погрешности дискретизации с дизерингом белым шумом. Синий — спектр погрешности дискретизации с дизерингом с более высокими частотами.
Итог
На этом первая часть серии заканчивается. Основные выводы:
- Дизеринг распределяет погрешность/отклонение дискретизации среди множества частот, и это зависит от функции дизеринга; они не сосредотачиваются в области низких частот.
- Восприятие человеком любого сигнала (звука, зрения) лучше всего работает в очень конкретных диапазонах частот. Сигналы часто избыточно дискретизируются на границах спектра восприятия, где восприятие малочувствительно. Например, стандартные частоты дискретизации звука позволяют воспроизводить сигналы, которые вообще не может услышать большинство взрослых. Из-за предыдущего пункта это делает очень привлекательной идею использования дизеринга и сдвига погрешностей в этот диапазон частот.
- Различные функции шума создают разные спектры погрешностей, которые можно использовать, зная, какой спектр погрешностей наиболее желателен.
В следующей части мы рассмотрим различные функции дизеринга — ту, которую я использовал в этой статье (ряд золотого сечения) и синий шум.