Как известно, в военное время значение косинуса может достигать трех. К счастью, это не касается простоты чисел - как ни бейся лбом об стену, число 17 простое и ни на что не делится, кроме себя и 1.
Или нет? Что, если мы грубо пошуруем ломиком в святая святых математики и подвигаем нетривиальные нули зета функции? Сдвинутся ли со своих мест простые числа? Вас ждут картинки и видео, и очень мало формул.
Я пропущу популярное изложение гипотезы Римана - это освещалось немыслимое количество раз. Перейдем сразу к концу: зная нетривиальные нули зета функции, можно 'обратным ходом' написать функцию, которая изображает pi(x) - 'prime counting function' - функцию, которая ступенчато увеличивается на единицу на каждом простом числе:
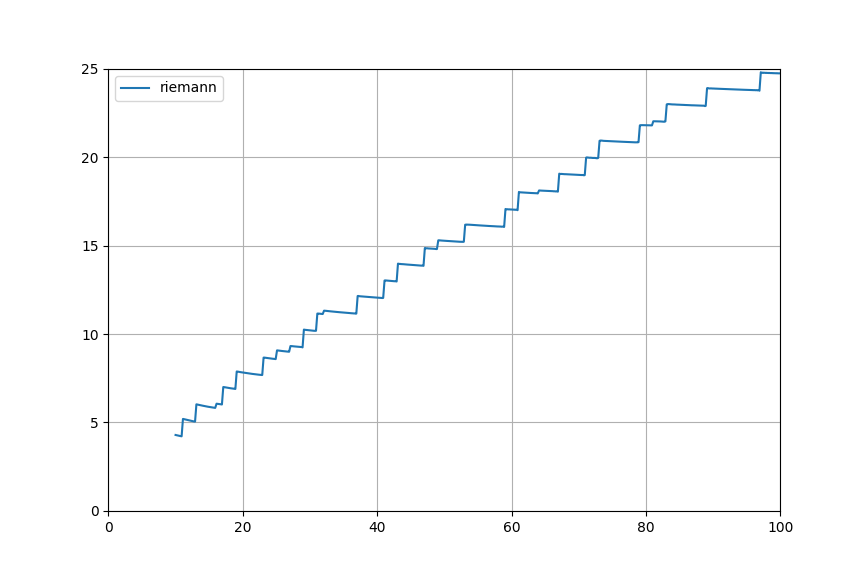
Там есть и маленькие ступеньки, их надо игнорировать, они соответствуют, в частности, степеням простых чисел. Если 'ловить' большие ступеньки, то мы получим магию:
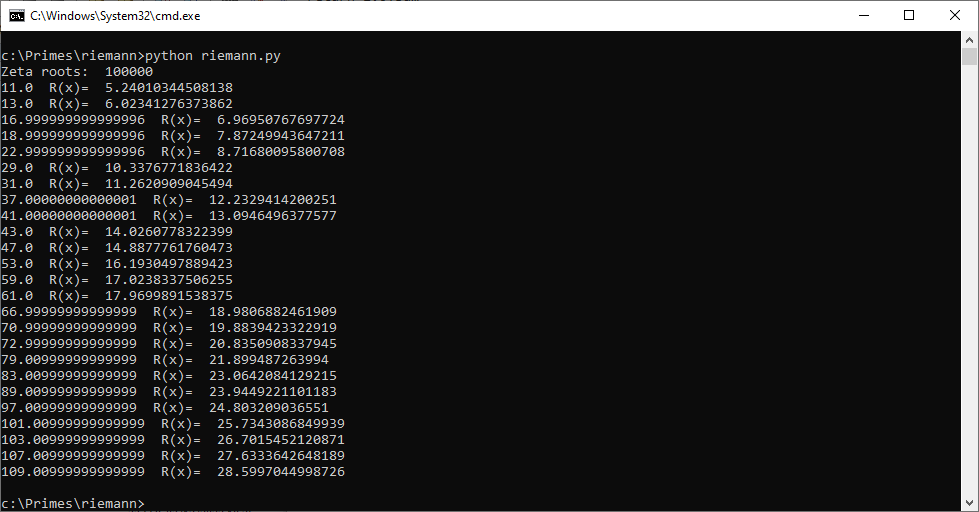
После немыслимо большого количества операций с плавающей точкой, логарифмов и косинусов, мы получаем простые числа... То, что можно сосчитать на пальцах, но магия в том, что они в этот раз приходят со стороны, где в общем-то с теорией чисел ничего не связано.
Формулы для расчета я брал тут и там тоже есть интересная анимация. Итак, основной 'ход' функции pi(x) задается выражением:
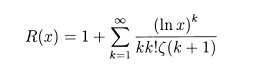
Эта часть корректируется слагаемым, отвечающим за тривиальные и нетривиальные нули (нижняя формула):
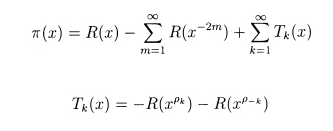
Со вторым выражением у меня почему-то получались очень большие значения (увы, не понял, почему) и я воспользовался выражением, которое должно быть эквивалентно (только названо C а не T), для C надо взять сумму по всем нетривиальным корням:
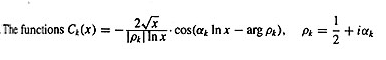
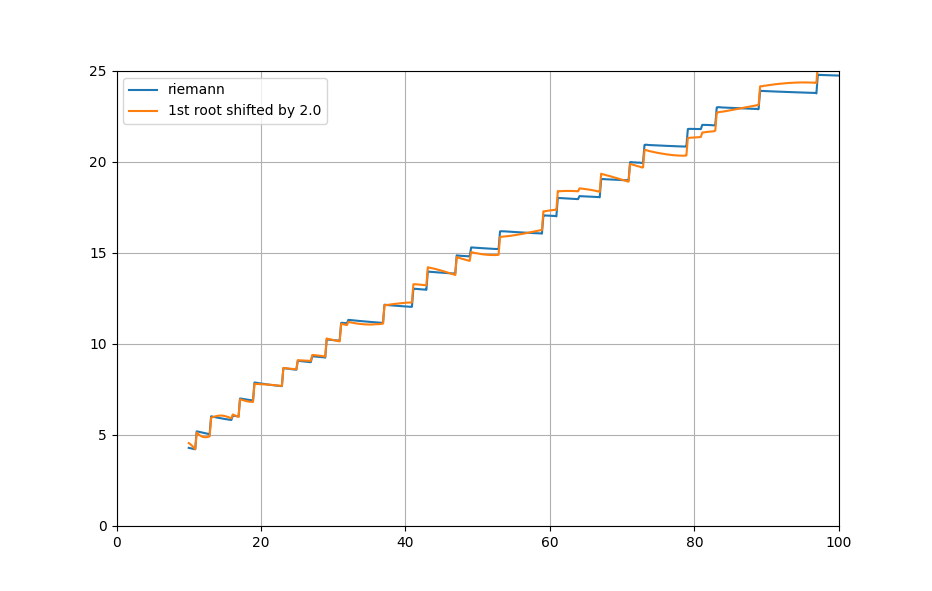
Я скачал 100K корней и запустил программу. Теперь настало время ломика. Возьмем первый корень и будем его сдвигать 'вверх' (то есть увеличивая мнимую часть, а для сопряженного корня - уменьшать):
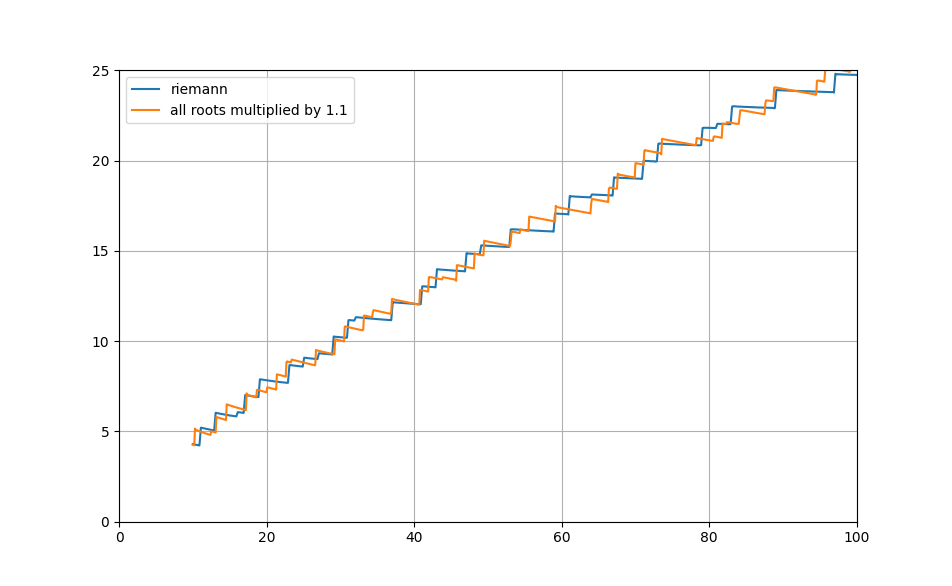
Теперь возьмем и подвинем так ВСЕ корни:
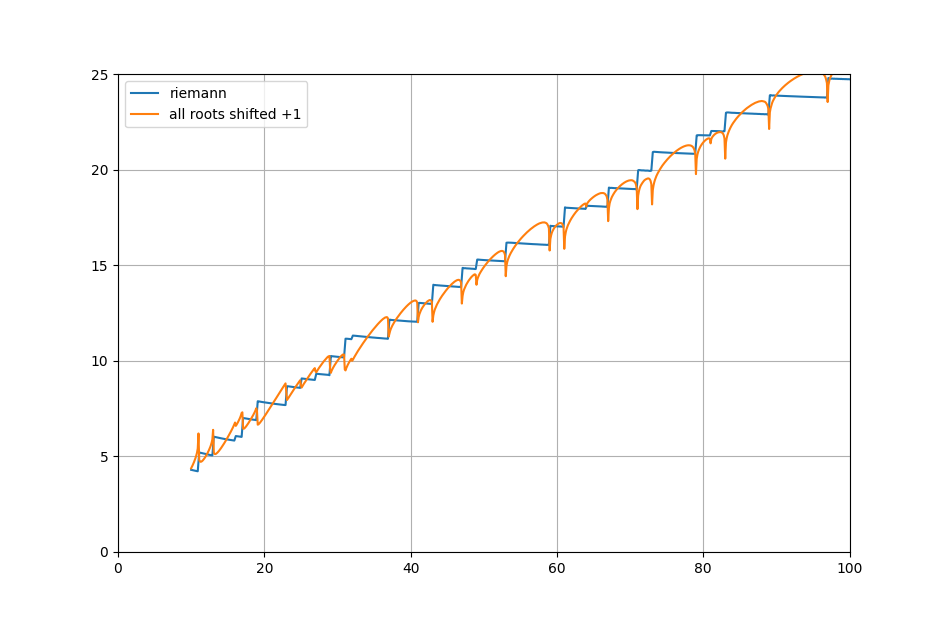
Заметьте, что ступеньки 'испортились', но остались на тех же местах. Сдвинуть простые числа можно только, если домножить мнимую часть нетривиальных корней на небольшую константу:
Наконец, пусть гипотеза Римана неверна. Сдвинем вещественную часть всех нетривиальных корней с их места, которое, как известно, 1/2:
Увы. Красивой анимации не будет. Ничего не поменялось, кроме третьей - четвертой цифры после запятой. Впрочем, это и неудивительно: если посмотреть формулы, то единственное место, где важна вещественная часть корня - это последняя формула, arg(Pk), но arg (фаза) и так почти вертикальна - даже для первого корня (0.5+14.13i) мнимая часть куда больше вещественной. Обратите внимание, что картинка выше не в масштабе. (Впрочем, может последняя формула выведена в предположении, что вещественная часть 0.5? Пусть более продвинутые коллеги меня поправят).
Итак, именно значения мнимой части определяют положения просты чисел, а знаменитая 'critical strip' в общем ни при чем.