Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Привет!
Очередной очерк. На этот раз поиграемся с комплексными числами, с формулами и их визуализацией.
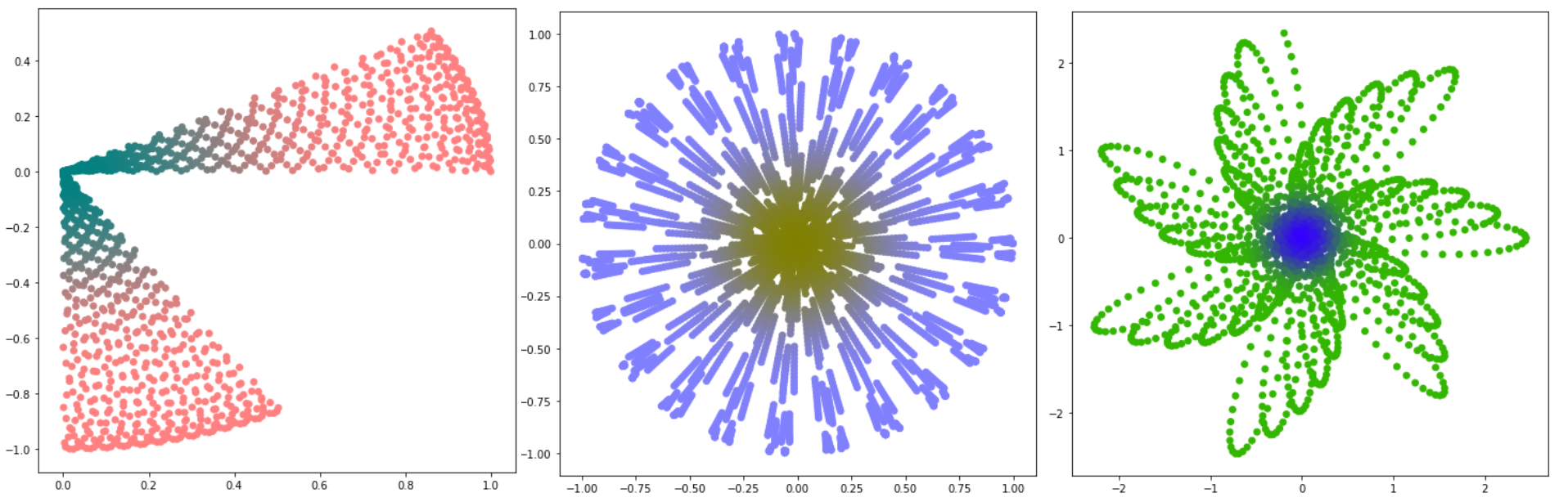
Комплексное число — это некоторое расширение вещественного числа, по сути вектор, для которого определено целое множество аксиом. Любое комплексное (а значит и вещественное) число можно записать в виде , где a — вещественная часть, b — мнимая, i — корень уравнения . Для него определено много операций, которые определены для вещественного числа, к примеру, . Интересно, что если проделывать различные операции с ними, возводить в степень, умножать и т. д. а затем брать (вещественную часть) для оси Ox, а (мнимую часть) для оси Oy, можно получать забавные картинки.
Кстати все следующие формулы я сам придумал.
Рутина. Функция, которая по данной итеративной функции рисует все на поле:
Все наши функции зависят от двух параметров A и B. Причем по B мы итерируемся внутри vis(), а A — глобальный параметр функции.
Ее объявление в python:
И запустим
И результат для A=121.5:

И для A=221.5:

Заметьте, эти числа вовсе не следуют из расчета какого-нибудь определенного интеграла на гладком многообразии и других умных бессмысленных в этом контексте слов. Это действительно рандомные числа, и существует еще ровно бесконечность разных A, в результате которых получается красота.
Объявим функцию цвета (такую функцию, которая по координатам возвращает tuple из трех чисел):
Выберем рандомный параметр A, пусть будет 149:

Гуси описываются так:
Объявление на python:
Ее результат для A=106:







Пока все.
Очередной очерк. На этот раз поиграемся с комплексными числами, с формулами и их визуализацией.

Идея
Комплексное число — это некоторое расширение вещественного числа, по сути вектор, для которого определено целое множество аксиом. Любое комплексное (а значит и вещественное) число можно записать в виде , где a — вещественная часть, b — мнимая, i — корень уравнения . Для него определено много операций, которые определены для вещественного числа, к примеру, . Интересно, что если проделывать различные операции с ними, возводить в степень, умножать и т. д. а затем брать (вещественную часть) для оси Ox, а (мнимую часть) для оси Oy, можно получать забавные картинки.
Кстати все следующие формулы я сам придумал.
Функция визуализации
Рутина. Функция, которая по данной итеративной функции рисует все на поле:
import random
import numpy as np
def vis(A, f, step=1.0, c=None):
x = []
y = []
for B in np.arange(0, A, step):
v = f(A, B)
x.append(v.real)
y.append(v.imag)
plt.figure(figsize=[8, 8])
mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5
x = np.array(x) / mxabs
y = np.array(y) / mxabs
if c is None:
plt.scatter(x, y)
else:
plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))])
plt.show()
Все наши функции зависят от двух параметров A и B. Причем по B мы итерируемся внутри vis(), а A — глобальный параметр функции.
Функция «Завитушки»
Ее объявление в python:
def func_1(A, B):
return math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))
И запустим
A = 121.5
vis(A, func_1, step=0.1)
И результат для A=121.5:

И для A=221.5:

Заметьте, эти числа вовсе не следуют из расчета какого-нибудь определенного интеграла на гладком многообразии и других умных бессмысленных в этом контексте слов. Это действительно рандомные числа, и существует еще ровно бесконечность разных A, в результате которых получается красота.
Надо покрасить
Объявим функцию цвета (такую функцию, которая по координатам возвращает tuple из трех чисел):
def sigm(x): # Эта функция позволяет нормализировать все что угодно от 0 до 1
return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2
color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2))
color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5)
Выберем рандомный параметр A, пусть будет 149:
vis(149, func_1, step=0.1, c=color_1)

Функция «Гуси»
Гуси описываются так:
Объявление на python:
def func_2(A, B):
return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))
Ее результат для A=106:

Функция «Фокачча»
def func_3(A, B):
return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A)))
vis(246, func_3, step=0.1, c=color_2)

vis(246, func_3, step=0.1, c=color_2)

Функция «Без названия»
color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2))
vis(162, func_4, step=0.1, c=color_3)

vis(179, func_4, step=0.1, c=color_3)

Формула красоты
def func_5(A, B):
return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A)))
color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2))
vis(345, func_5, step=0.1, c=color_4)

vis(350, func_5, step=0.1, c=color_4)

Пока все.
Весь код
import numpy as np
import random
import matplotlib.pyplot as plt
import math
def vis(A, f, step=1.0, c=None):
x = []
y = []
for B in np.arange(0, A, step):
v = f(A, B)
x.append(v.real)
y.append(v.imag)
plt.figure(figsize=[7, 7])
mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5
x = np.array(x) / mxabs
y = np.array(y) / mxabs
if c is None:
plt.scatter(x, y)
else:
plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))])
plt.show()
def func_1(A, B):
return math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))
def func_2(A, B):
return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A)))
def func_3(A, B):
return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A)))
def func_4(A, B):
return math.sin(A + B) * B * math.e ** (1j * B * math.sin(A))
def func_5(A, B):
return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A)))
def sigm(x):
return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2
color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2))
color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5)
color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2))
color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2))
colors = [color_1, color_2, color_3, color_4]
funcs = [func_1, func_2, func_3, func_4, func_5]
while True:
col = random.choice(colors)
func = random.choice(funcs)
vis(random.random() * 200 + 100, func, step=0.1, c=col)
if input() == "exit":
break
Еще скриншоты






















