Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В ходе обсуждения достоинств и недостатков нового революционного формата с плавающей запятой Posit было cделано заявление, что вообще-то задача Posit — компактно хранить данные, а вовсе не использоваться в вычислениях; при этом сами вычисления делаются в арифметике Quire с бо́льшей точностью, которая также входит в стандарт Posit.
Ну, хранить так хранить. Что вообще значит — «хранить» числа после вычислений, выполненных с бо́льшей точностью, чем допускает формат хранения? Это значит — округлять, а округлять значит вносить погрешности. Погрешности можно оценивать разными способами — и чтобы не повторяться, сегодня мы используем спектральный анализ с помощью преобразования Фурье.
Если взять сигнал в виде синусоиды и выполнить над ним преобразование Фурье, то в спектре мы должны получить один-единственный пик; по факту же в спектре могут присутствовать как гармоники с частотой кратной основному тону, полученных вследствие нелинейных искажений, так и шумовая полка, полученная в следствие шумов, наводок и оцифровки. Вот уровень этих шумов мы и будем измерять.
Чтобы было ещё интереснее, в качестве тестового сигнала возьмём не одну синусоиду, а несколько; при этом необходимо следить, чтобы периоды этих синусоид нацело укладывались в период дискретного преобразование Фурье. В Wolfram Mathematica это можно сделать, например, так:
Простые числа здесь используются для неравномерного прореживания частот; а j*j сдвигает фазу синусоиды в зависимости от частоты во избежание сильных выбросов в тестовом сигнале, обеспечивая ему более-менее равномерную амплитуду. Визуально полученный сигнал выглядит вот так:
Далее мы нормируем его к единице по максимальному значению, затем преобразуем в целочисленный 32-битный Int, Float, Posit и снова в Double. Если утверждения авторов верны, то погрешность, вносимая преобразованием Double→Posit→Double будет ближе к Doublе, чем к Float.
Уровень шумов будем анализировать в стандартных для обработки сигналов единицах — децибелах, позволяющих сравнивать величины в логарифмическом масштабе. В качестве инструмента я использовал собственный спектроанализатор, когда-то написанный в исследовательских целях.
Итак:
синий — Float
красный — Posit
фиолетовый — Int32
голубой — Double
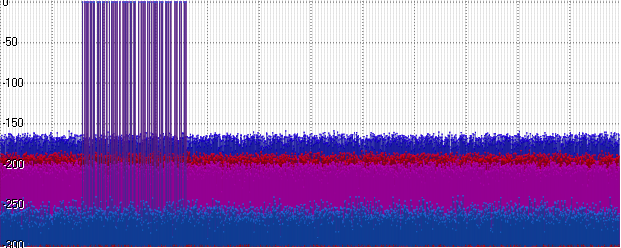
Posit, конечно, оказался чуточку лучше Float — но до уровня Double ему ещё далеко. И при этом — хуже Int32! Логично — ведь часть бит у него уходит на порядок… Давайте используем этот порядок — увеличим амплитуду нашего сигнала до 1000:
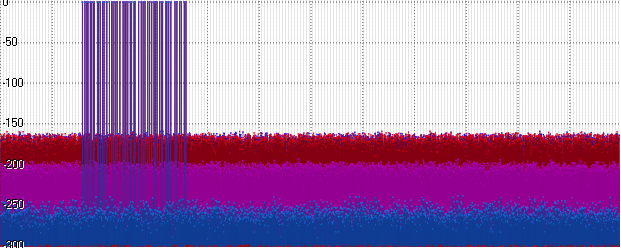
Внезапно (а на самом деле вполне ожидаемо) шум у Float и Posit сравнялся. Идём дальше — увеличиваем амплитуду до миллиарда:
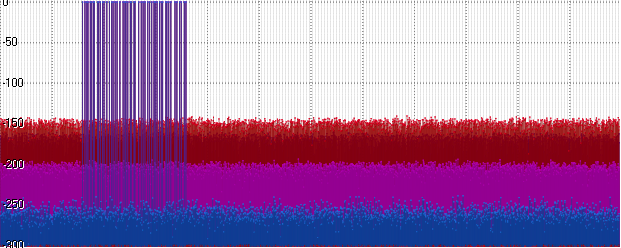
Float показывает тот же уровень, а Posit начинает отставать. Дальнейшее увеличение амплитуды (здесь 1015) приводит к дальнейшему повышению шумовой полки:
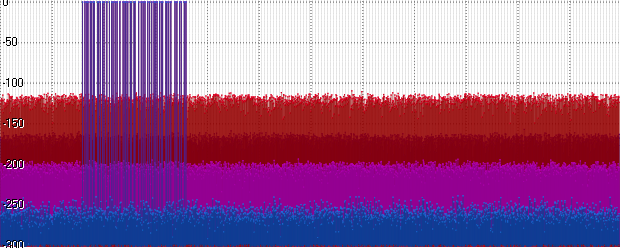
Чуда опять не произошло. Проведённый спектральный анализ не смог подтвердить заявления авторов о том, что использование формата Posit в качестве хранения может обеспечить точность близкую к Double. Даже в наилучших условиях шумовая полка у Posit оказались лишь на 20 децибел ниже Float, но при этом выше Int32 на 10 децибел, и выше Double — на 60 децибел.
Конечно, Posit-у вполне можно найти полезное применение — в качестве защиты от выхода за пределы допустимого диапазона, когда выбросы, значительно превосходящие нормальные значения, не будут приводить ни к клиппингу, ни к переполнению. Но даже в таком сценарии Posit выступает скорее как компромисс между Int и Float, а вовсе не однозначно лучший формат чисел.
Ну, хранить так хранить. Что вообще значит — «хранить» числа после вычислений, выполненных с бо́льшей точностью, чем допускает формат хранения? Это значит — округлять, а округлять значит вносить погрешности. Погрешности можно оценивать разными способами — и чтобы не повторяться, сегодня мы используем спектральный анализ с помощью преобразования Фурье.
Очень краткое введение
Если взять сигнал в виде синусоиды и выполнить над ним преобразование Фурье, то в спектре мы должны получить один-единственный пик; по факту же в спектре могут присутствовать как гармоники с частотой кратной основному тону, полученных вследствие нелинейных искажений, так и шумовая полка, полученная в следствие шумов, наводок и оцифровки. Вот уровень этих шумов мы и будем измерять.
Начало
Чтобы было ещё интереснее, в качестве тестового сигнала возьмём не одну синусоиду, а несколько; при этом необходимо следить, чтобы периоды этих синусоид нацело укладывались в период дискретного преобразование Фурье. В Wolfram Mathematica это можно сделать, например, так:
sz = 8192;
data = Table[2 Sum[
Sin[Prime[j] k 2 Pi/sz + j*j]/sz,
{j, 100, 200, 2}] // N,
{k, 0, sz - 1}];Простые числа здесь используются для неравномерного прореживания частот; а j*j сдвигает фазу синусоиды в зависимости от частоты во избежание сильных выбросов в тестовом сигнале, обеспечивая ему более-менее равномерную амплитуду. Визуально полученный сигнал выглядит вот так:

Далее мы нормируем его к единице по максимальному значению, затем преобразуем в целочисленный 32-битный Int, Float, Posit и снова в Double. Если утверждения авторов верны, то погрешность, вносимая преобразованием Double→Posit→Double будет ближе к Doublе, чем к Float.
Уровень шумов будем анализировать в стандартных для обработки сигналов единицах — децибелах, позволяющих сравнивать величины в логарифмическом масштабе. В качестве инструмента я использовал собственный спектроанализатор, когда-то написанный в исследовательских целях.
сравнительная таблица
| Порог слышимости | 0 дБ |
| Шелест листьев | 10 дБ |
| Шепот | 20 дБ |
| Тиканье часов | 30 дБ |
| Тихая комната | 40 дБ |
| Тихая улица | 50 дБ |
| Разговор | 60 дБ |
| Шумная улица | 70 дБ |
| Опасный для здоровья уровень | 75 дБ |
| Пневматический молоток | 90 дБ |
| Поезд метро | 100 дБ |
| Громкая музыка | 110 дБ |
| Болевой порог | 120 дБ |
| Сирена | 130 дБ |
| Старт ракеты | 150 дБ |
| Смертельный уровень | 180 дБ |
| Шумовое оружие | 200 дБ |
Итак:
синий — Float
красный — Posit
фиолетовый — Int32
голубой — Double

Posit, конечно, оказался чуточку лучше Float — но до уровня Double ему ещё далеко. И при этом — хуже Int32! Логично — ведь часть бит у него уходит на порядок… Давайте используем этот порядок — увеличим амплитуду нашего сигнала до 1000:

Внезапно (а на самом деле вполне ожидаемо) шум у Float и Posit сравнялся. Идём дальше — увеличиваем амплитуду до миллиарда:

Float показывает тот же уровень, а Posit начинает отставать. Дальнейшее увеличение амплитуды (здесь 1015) приводит к дальнейшему повышению шумовой полки:

Заключение
Чуда опять не произошло. Проведённый спектральный анализ не смог подтвердить заявления авторов о том, что использование формата Posit в качестве хранения может обеспечить точность близкую к Double. Даже в наилучших условиях шумовая полка у Posit оказались лишь на 20 децибел ниже Float, но при этом выше Int32 на 10 децибел, и выше Double — на 60 децибел.
Конечно, Posit-у вполне можно найти полезное применение — в качестве защиты от выхода за пределы допустимого диапазона, когда выбросы, значительно превосходящие нормальные значения, не будут приводить ни к клиппингу, ни к переполнению. Но даже в таком сценарии Posit выступает скорее как компромисс между Int и Float, а вовсе не однозначно лучший формат чисел.






