Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В 1980 году Intel представила чип 8087 для ускорения обработки чисел с плавающей запятой на 8086-х процессорах, и его использовали в оригинальном IBM PC. Поскольку первые микропроцессоры работали только с целыми числами, арифметика с числами с плавающей запятой была медленной, а с трансцендентными функциями вроде арктангенса или логарифмов дела обстояли ещё хуже. Добавление чипа сопроцессора 8087 к системе было способно ускорить операции с числами с плавающей запятой до ста раз.
Я вскрыл чип 8087 и сделал несколько его фотографий под микроскопом. На фото ниже показан крохотный кремниевый кристалл чипа. По его бокам крохотные проводники соединяют его с 40 внешними ногами. Разметка основных функциональных блоков на картинке сделана мною благодаря реверс-инжинирингу. Если внимательно изучить чип, то можно извлечь из его ПЗУ различные константы – такие числа, как π, используемые чипом в вычислениях.
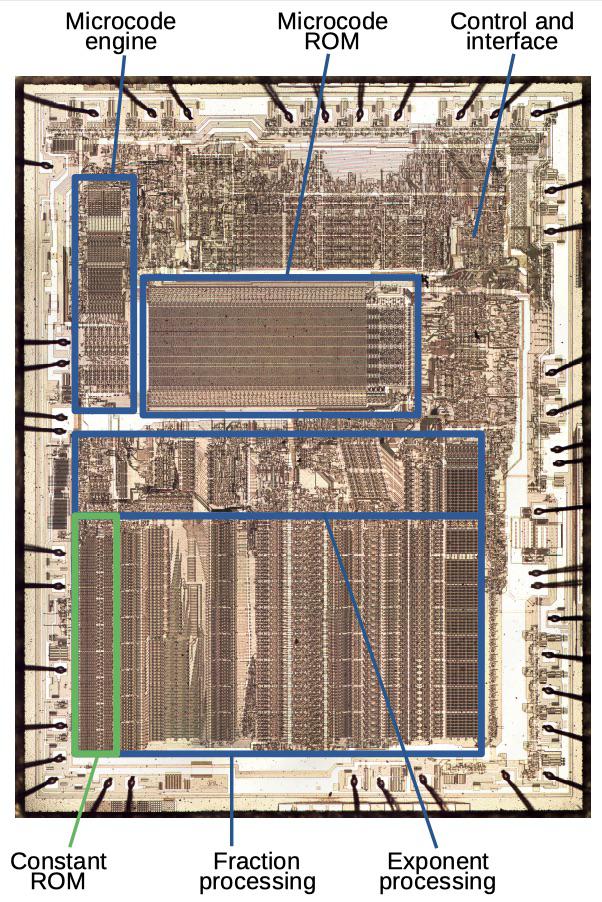
Кристалл чипа от Intel 8087 для работы с плавающей запятой с отмеченными основными функциональными блоками. ПЗУ с константами отмечен зелёным. Кликабельно.
В верхней половине чипа находятся управляющие схемы. Для выполнения инструкции с плавающей запятой может потребоваться до 1000 шагов; для описания этих шагов 8087 использовал микрокод. На фото кристалла видно «механизм», запускавший программу из микрокода; по сути, это простой CPU. Рядом с ним находится большой ПЗУ, где хранится микрокод.
В нижней части кристалла находятся схемы, обрабатывающие числа с плавающей запятой. Число с плавающей запятой состоит из дробной части (также известной, как значащая часть числа или мантисса), экспоненты и знакового бита. В десятичной записи у числа 6,02×1023 6,02 будет мантиссой, а 23 – экспонентой. Отдельные схемы чипа параллельно обрабатывают мантиссу и экспоненту. Схема обработки мантиссы поддерживает 67-битные значения – 64-битную мантиссу и три дополнительных бита для точности. Слева направо, схемы работы с мантиссой состоят из ПЗУ с константами, сдвигового регистра, сумматора/вычитателя и стека регистров. Тема данной статьи – ПЗУ с константами, на фото оно выделено зелёным.
8087 работал в качестве сопроцессора к процессору 8086. Когда процессор 8086 сталкивался с особой инструкцией, относившейся к числам с плавающей запятой, он её игнорировал и давал 8087-му возможность выполнить её параллельно. Взаимодействие 8086 и 8087 было устроено довольно хитрым образом. Если упрощённо, то 8087 смотрит за потоком инструкций 8086, и выполняет любые инструкции, относящиеся к 8087. Сложность в том, что у 8086 есть буфер упреждающей выборки инструкций, поэтому та инструкция, которую в данный момент получает 8086, не совпадает с той, которую он исполняет. Поэтому 8087 дублировал буфер упреждающей выборки инструкций 8086 (или менее крупный буфер упреждающей выборки инструкций 8088), чтобы знать, чем занят 8086 (подробнее описано тут). Ещё одна трудность связана со сложными режимами адресации 8086, использующими регистры внутри 8086. 8087 не может выполнять эти режимы адресации, поскольку у него нет доступа к регистрам 8086. Вместо этого, когда 8086 видит инструкцию для 8087, он запрашивает данные из указанного места в памяти и игнорирует результат. Тем временем 8087 берёт адрес с шины, на случай, если он ему понадобится. Вам может показаться, что в этом месте образуется ловушка, если 8087 не будет установлен – однако этого не случится. В системе без 8087 компоновщик переписывает инструкции 8087, заменяя их вызовами подпрограмм из библиотеки эмуляции.
Не буду в подробностях рассказывать внутреннюю работу 8087, но в целом операции с плавающей запятой реализованы через сложения, вычитания и сдвиги целых. Для сложения или вычитания двух чисел с плавающей запятой 8087 сдвигает числа, пока не выровняются двоичные запятые (как десятичные запятые, только в двоичной системе), а потом складывает или вычитает мантиссу. Умножение, деление и взятие квадратного корня выполняются посредством последовательных сдвигов и сложений/вычитаний. Трансцендентные функции (тангенс, арктангенс, логарифм, степень) используют алгоритмы CORDIC, которые для повышения эффективности вычислений используют сдвиги и сложения особых констант.
В данной статье описан ПЗУ, где хранятся константы. Не стоит путать его с более крупным четырёхуровневым ПЗУ, где хранится микрокод – этот последний реализован при помощи необычной технологии, хранящей по два бита на транзистор. Это делается при помощи транзисторов трёх разных размеров или отсутствия транзистора на каждой позиции. Эти четыре варианта обозначают два бита. Эта сложная технология была необходима для того, чтобы уместить крупный ПЗУ на кристалл 8087.
ПЗУ для констант использует стандартные технологии для хранения констант (таких, как π, ln(2) и √2), требуемых 8087 для вычислений. На фото ниже приведена часть ПЗУ с константами. Чтобы было видно сам кристалл, с него удалён металлический слой. Розоватые участки – это кремний с примесями, дающими ему разные свойства, а красноватые и зеленоватые линии – это поликремний, особый тип кремниевой проводки, лежащий сверху. Обратите внимание на структуру ПЗУ, похожую на правильную решётку. ПЗУ состоит из двух столбцов транзисторов, хранящих биты. Чтобы объяснить схему его работы, начну со схемы работы транзистора.

Часть ПЗУ с константами, с удалённым металлическим слоем. Три столбца более крупных транзисторов используются для выбора рядов.
Интегральные схемы (ИС) высокой плотности в 1970-х обычно делали из транзисторов типа N-МОП. (Современные компьютеры делают из КМОП, состоящих из N-МОП и из P-МОП обратной к ним полярности). На диаграмме ниже показана структура N-МОП-транзистора. ИС собран из кремниевой подложки, на которой создаются транзисторы. На участки кремния добавляются примеси, создающие «диффузные» регионы с нужными электрическими свойствами. Транзистор можно считать переключателем, который позволяет току течь между двумя участками диффузии, которые называются исток и сток. Транзистором управляет затвор, сделанный из кремния особого типа – поликремния. Подача напряжения на затвор позволяет току течь между истоком и стоком; в противном случае ток не течёт. Кристалл 8087 довольно сложный, на нём находится порядка 40 000 таких транзисторов.
В разных источниках даётся разное количество транзисторов на 8087: Intel говорит о 40 000, в Википедии написано про 45 000. Возможно, всё дело в разных способах подсчёта. Поскольку количество транзисторов в ПЗУ, PLA или другой подобной структуре зависит от хранящихся данных, в источниках часто указывают количество «потенциальных» транзисторов вместо реальных. Также можно считать или не считать подтягивающие транзисторы, или считать высокотоковые драйверы за один транзистор или за несколько параллельных.
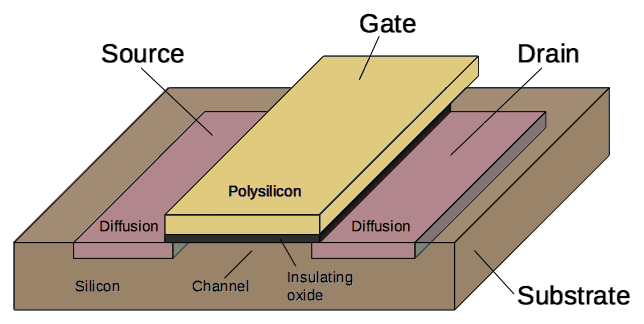
МОП-структура, реализованная в ИС
Увеличив масштаб, можно рассмотреть отдельные транзисторы ПЗУ. Розоватые участки – это кремний с примесями, формирующими истоки и стоки. Вертикальные шины выборки [select lines] поликремния формируют затворы транзисторов. Отмеченные участки кремния соединены с землёй, и притягивают вниз одну сторону каждого транзистора. Кружочки – это VIA, межслойное переходное отверстие между кремнием и металлическими шинами выше. Для фото металлические шины удалены; местоположение одной из них показано оранжевой линией.

Часть ПЗУ с константами. Каждая шина выборки выбирает определённую константу. Транзисторы показаны жёлтыми символами. Х отмечает отсутствующий транзистор, соответствующий биту 0. Оранжевая линия показывает местоположение металлического проводника.
Важной особенностью ПЗУ является отсутствие некоторых транзисторов – нет первого в верхнем ряду, и двух, отмеченных Х, в нижнем. Биты программируются в ПЗУ через изменение схемы добавления примесей в кремний, которые создают транзисторы или оставляют изолирующие участки. Каждый имеющийся или отсутствующий транзистор обозначает один бит. При активации шины выборки все транзисторы в этом столбце открываются, притягивая вниз соответствующие выходные шины. Но если в выбранной позиции транзистора нет, соответствующий выход останется высоким. Таким образом, значение читается из ПЗУ путём активации шины выборки, которая выдаёт это значение из ПЗУ на выходные шины.
ПЗУ с константами состоит из 143 рядов и 21 столбца. Он содержит 134 ряда по 21 биту, кроме одного кусочка 6×6 транзисторов слева вверху. Поэтому физический размер ПЗУ с константами составляет 2946 бит.

Исходя из схемы ПЗУ, отсутствующая секция означает, что первые 12 констант 64-битные, а не 67-битные. Это константы, не относящиеся к CORDIC, и им, видимо, не требуется дополнительная точность.
Под микроскопом видна схема битов ПЗУ, поэтому её можно оттуда извлечь. Однако совершенно неочевидно, как эти биты потом интерпретировать. Первый вопрос – обозначает ли наличие транзистора 0 или 1 (позже оказалось, что наличие транзистора – это 1). Вторая проблема – как перевести сетку битов 134×21 в значения.
Кодирование битов можно определить двумя способами. Первый – отследить схему, читающую данные из ПЗУ и посмотреть, как они используются. Второй – искать закономерности в сырых данных и попытаться их осмыслить. Поскольку 8087 очень сложный, я хотел избежать полного реверс-инжиниринга при изучении констант, поэтому я использовал второй подход.
Путь передачи данных чипа состоит из 67 горизонтальных рядов, поэтому было ясно, что 134 ряда в ПЗУ соответствуют двум наборам 67-битных констант. Я извлёк один набор констант из нечётных рядов, а другой – из чётных, однако полученные значения не имели смысла. Подумав ещё немного, я понял, что ряды не чередовались, а шли в повторяющемся порядке ABBA.
Ряды шли в порядке ABBAABBAABBA…, где в рядах А содержались биты для одного набора констант, а в рядах В – для другого. Такая схема использовалась вместо простого чередования АВАВ, возможно, потому, что один контакт может управлять двумя соседними транзисторами. То есть, один проводник может выбрать каждую из групп АА и ВВ.
Когда я учёл порядок АВВА, я получил кучу знакомых констант, включая π и 1. На диаграмме ниже показаны биты из этих констант. На фото бит 1 – зелёная полоска, бит 0 – красная. В двоичной системе π равно 11,001001..., и именно это значение видно в верхнем ряду размеченных битов. Нижнее значение – это константа 1.

Верхний ряд битов – число π, нижний – 1. Эта диаграмма повёрнута на 90° по сравнению с остальными.
Следующая сложность с интерпретацией состоит в том, что в ПЗУ хранятся только мантиссы, но не экспоненты (пока что я не нашёл отдельный ПЗУ с экспонентами). И я экспериментировал с различными экспонентами, пока не получал осмысленных значений. Некоторые были понятны сразу: к примеру, константа 1,204120 даёт log10 (2) с использованием экспоненты 2-2. Другие понять было посложнее, например, 1,734723. В итоге, я понял, что 1,734723×259 = 1018. Зачем в 8087 содержится такая константа? Возможно потому, что 8087 поддерживает упакованный двоично-десятичный код с 18 знаками.
Некоторые экспоненты было очень трудно найти, и я использовал метод перебора, чтобы посмотреть, не выдаст ли результат какой-нибудь логарифм или степень какого-то числа. Сложнее всего было определить константу для ln(2)/3. Важность этого числа мне непонятна.
Вот полный список констант из ПЗУ. Столбец «смысл» – это моё описание значения.
Не уверен, почему 1018 повторяется – возможно, отличие в экспоненте.
Физически константы расположены тремя группами. Первая группа – это значения, которые пользователь может загружать (1, π, log210, log2e, log102, и ln), а также значения для внутреннего использования (1018, ln(2)/3, 3*log2(e), log2(e) и √2). Вторая группа состоит из 16 констант арктангенса, а третья – из 14 констант log2.
В 8087 есть семь инструкций для прямой загрузки констант. Инструкции FDLZ, FLD1, FLDPI, FLD2T, FLD2E, FLDLG2 и FLDLN2 загружают в стек константы 0, 1, π, log210, log2e, log102 и ln 2 соответственно. Все эти константы кроме 0 хранятся в ПЗУ.
Последние две группы констант используются для подсчёта трансцендентных функций по алгоритмам CORDIC.
По константам из ПЗУ можно узнать о некоторых деталях работы алгоритмов 8087. В ПЗУ содержится 16 значений для арктангенса, арктангенсы от 2-n. Также там хранится 14 логарифмов по основанию 2 от (1+2-n). Такие значения могут показаться необычными, однако они используются в эффективном алгоритме CORDIC, изобретённом в 1958 году.
Идея CORDIC состоит в том, что вычислить тангенс и арктангенс можно через разбиение угла на меньшие с поворотом вектора на эти углы. Фокус в том, что если правильно выбирать меньшие углы, то каждый поворот можно будет вычислить через эффективные сдвиги и сложения вместо тригонометрических функций. Допустим, нам нужно найти find tan(z). Мы можем разбить z на сумму небольших углов: z ≈ {atan(2-1) or 0} + {atan(2-2) or 0} + {atan(2-3) or 0} +… + {atan(2-16 or 0}. Поворачивать вектор, допустим, на atan(2-2) можно, умножая на 2-2 и складывая. Суть в том, что умножение на 2-2 осуществляется через быстрый побитовый сдвиг. Учитывая всё это, вычислить tan(z) можно, сравнивая z с константами atan, а потом пройдя 16 циклов сложений и сдвигов, что на железе делается быстро. Поэтому константы для atan предварительно подсчитаны и хранятся в ПЗУ. Арктангенс вычисляется сходным образом, только наоборот – в процессе поворотов углы (из ПЗУ с константами) суммируются и дают итоговый.
При вычислении логарифма и экспоненты также используются алгоритмы CORDIC и соответствующие им логарифмические константы. Главное тут то, что умножение на (1 + 2-n) можно делать быстро при помощи сдвигов и сложений. Логарифм и экспоненту можно вычислить, умножая одну сторону уравнения на последовательность значений и добавляя соответствующие логарифмические константы к другой. По алгоритмам вычисления логарифма и экспоненты документации для 8087 я не нашёл. Думаю, что они похожи на те, что описаны в следующей статье, только 8087 использует основание 2 вместо е. Не пойму, почему у 8087 нет константы log2 (1 + 2-1), необходимой для того алгоритма.
Поддержка трансцендентных функций в 8087 не такая уж и обширная, как можно было ожидать. Он поддерживает только тангенс и арктангенс, без синусов и косинусов. Для вычисления последних придётся применять тригонометрические тождества. Логарифмы и экспоненты поддерживают только основание 2 – для оснований 10 или е пользователю придётся применять масштабный коэффициент. В своё время 8087 расширил пределы ёмкости чипов, поэтому количество инструкций было сведено к минимуму.
8087 – это сложный чип, и на первый взгляд похож на безнадёжно запутанный лабиринт. Однако по большей части в нём можно разобраться после тщательного изучения. В его ПЗУ хранится 42 константы, и их значения можно извлечь при помощи микроскопа. Некоторые константы (например, π) были ожидаемы, другие же (например, ln(2)/3) вызывают больше вопросов. Многие из констант используются для вычисления тангенсов, арктангенсов, логарифмов и степеней при помощи алгоритмов CORDIC.

Фото кристалла 8087 без металлического слоя. Кликабельно.
Хотя Intel 8087 для работы с плавающей запятой представили 40 лет назад, его влияние ощущается до сих пор. Он породил стандарт IEEE 754 для чисел с плавающей запятой, используемый в большей части арифметических вычислений, а инструкции 8087 остаются частью процессоров х86, используемых в большинстве компьютеров.
Я вскрыл чип 8087 и сделал несколько его фотографий под микроскопом. На фото ниже показан крохотный кремниевый кристалл чипа. По его бокам крохотные проводники соединяют его с 40 внешними ногами. Разметка основных функциональных блоков на картинке сделана мною благодаря реверс-инжинирингу. Если внимательно изучить чип, то можно извлечь из его ПЗУ различные константы – такие числа, как π, используемые чипом в вычислениях.

Кристалл чипа от Intel 8087 для работы с плавающей запятой с отмеченными основными функциональными блоками. ПЗУ с константами отмечен зелёным. Кликабельно.
В верхней половине чипа находятся управляющие схемы. Для выполнения инструкции с плавающей запятой может потребоваться до 1000 шагов; для описания этих шагов 8087 использовал микрокод. На фото кристалла видно «механизм», запускавший программу из микрокода; по сути, это простой CPU. Рядом с ним находится большой ПЗУ, где хранится микрокод.
В нижней части кристалла находятся схемы, обрабатывающие числа с плавающей запятой. Число с плавающей запятой состоит из дробной части (также известной, как значащая часть числа или мантисса), экспоненты и знакового бита. В десятичной записи у числа 6,02×1023 6,02 будет мантиссой, а 23 – экспонентой. Отдельные схемы чипа параллельно обрабатывают мантиссу и экспоненту. Схема обработки мантиссы поддерживает 67-битные значения – 64-битную мантиссу и три дополнительных бита для точности. Слева направо, схемы работы с мантиссой состоят из ПЗУ с константами, сдвигового регистра, сумматора/вычитателя и стека регистров. Тема данной статьи – ПЗУ с константами, на фото оно выделено зелёным.
8087 работал в качестве сопроцессора к процессору 8086. Когда процессор 8086 сталкивался с особой инструкцией, относившейся к числам с плавающей запятой, он её игнорировал и давал 8087-му возможность выполнить её параллельно. Взаимодействие 8086 и 8087 было устроено довольно хитрым образом. Если упрощённо, то 8087 смотрит за потоком инструкций 8086, и выполняет любые инструкции, относящиеся к 8087. Сложность в том, что у 8086 есть буфер упреждающей выборки инструкций, поэтому та инструкция, которую в данный момент получает 8086, не совпадает с той, которую он исполняет. Поэтому 8087 дублировал буфер упреждающей выборки инструкций 8086 (или менее крупный буфер упреждающей выборки инструкций 8088), чтобы знать, чем занят 8086 (подробнее описано тут). Ещё одна трудность связана со сложными режимами адресации 8086, использующими регистры внутри 8086. 8087 не может выполнять эти режимы адресации, поскольку у него нет доступа к регистрам 8086. Вместо этого, когда 8086 видит инструкцию для 8087, он запрашивает данные из указанного места в памяти и игнорирует результат. Тем временем 8087 берёт адрес с шины, на случай, если он ему понадобится. Вам может показаться, что в этом месте образуется ловушка, если 8087 не будет установлен – однако этого не случится. В системе без 8087 компоновщик переписывает инструкции 8087, заменяя их вызовами подпрограмм из библиотеки эмуляции.
Не буду в подробностях рассказывать внутреннюю работу 8087, но в целом операции с плавающей запятой реализованы через сложения, вычитания и сдвиги целых. Для сложения или вычитания двух чисел с плавающей запятой 8087 сдвигает числа, пока не выровняются двоичные запятые (как десятичные запятые, только в двоичной системе), а потом складывает или вычитает мантиссу. Умножение, деление и взятие квадратного корня выполняются посредством последовательных сдвигов и сложений/вычитаний. Трансцендентные функции (тангенс, арктангенс, логарифм, степень) используют алгоритмы CORDIC, которые для повышения эффективности вычислений используют сдвиги и сложения особых констант.
Реализация ПЗУ
В данной статье описан ПЗУ, где хранятся константы. Не стоит путать его с более крупным четырёхуровневым ПЗУ, где хранится микрокод – этот последний реализован при помощи необычной технологии, хранящей по два бита на транзистор. Это делается при помощи транзисторов трёх разных размеров или отсутствия транзистора на каждой позиции. Эти четыре варианта обозначают два бита. Эта сложная технология была необходима для того, чтобы уместить крупный ПЗУ на кристалл 8087.
ПЗУ для констант использует стандартные технологии для хранения констант (таких, как π, ln(2) и √2), требуемых 8087 для вычислений. На фото ниже приведена часть ПЗУ с константами. Чтобы было видно сам кристалл, с него удалён металлический слой. Розоватые участки – это кремний с примесями, дающими ему разные свойства, а красноватые и зеленоватые линии – это поликремний, особый тип кремниевой проводки, лежащий сверху. Обратите внимание на структуру ПЗУ, похожую на правильную решётку. ПЗУ состоит из двух столбцов транзисторов, хранящих биты. Чтобы объяснить схему его работы, начну со схемы работы транзистора.

Часть ПЗУ с константами, с удалённым металлическим слоем. Три столбца более крупных транзисторов используются для выбора рядов.
Интегральные схемы (ИС) высокой плотности в 1970-х обычно делали из транзисторов типа N-МОП. (Современные компьютеры делают из КМОП, состоящих из N-МОП и из P-МОП обратной к ним полярности). На диаграмме ниже показана структура N-МОП-транзистора. ИС собран из кремниевой подложки, на которой создаются транзисторы. На участки кремния добавляются примеси, создающие «диффузные» регионы с нужными электрическими свойствами. Транзистор можно считать переключателем, который позволяет току течь между двумя участками диффузии, которые называются исток и сток. Транзистором управляет затвор, сделанный из кремния особого типа – поликремния. Подача напряжения на затвор позволяет току течь между истоком и стоком; в противном случае ток не течёт. Кристалл 8087 довольно сложный, на нём находится порядка 40 000 таких транзисторов.
В разных источниках даётся разное количество транзисторов на 8087: Intel говорит о 40 000, в Википедии написано про 45 000. Возможно, всё дело в разных способах подсчёта. Поскольку количество транзисторов в ПЗУ, PLA или другой подобной структуре зависит от хранящихся данных, в источниках часто указывают количество «потенциальных» транзисторов вместо реальных. Также можно считать или не считать подтягивающие транзисторы, или считать высокотоковые драйверы за один транзистор или за несколько параллельных.

МОП-структура, реализованная в ИС
Увеличив масштаб, можно рассмотреть отдельные транзисторы ПЗУ. Розоватые участки – это кремний с примесями, формирующими истоки и стоки. Вертикальные шины выборки [select lines] поликремния формируют затворы транзисторов. Отмеченные участки кремния соединены с землёй, и притягивают вниз одну сторону каждого транзистора. Кружочки – это VIA, межслойное переходное отверстие между кремнием и металлическими шинами выше. Для фото металлические шины удалены; местоположение одной из них показано оранжевой линией.

Часть ПЗУ с константами. Каждая шина выборки выбирает определённую константу. Транзисторы показаны жёлтыми символами. Х отмечает отсутствующий транзистор, соответствующий биту 0. Оранжевая линия показывает местоположение металлического проводника.
Важной особенностью ПЗУ является отсутствие некоторых транзисторов – нет первого в верхнем ряду, и двух, отмеченных Х, в нижнем. Биты программируются в ПЗУ через изменение схемы добавления примесей в кремний, которые создают транзисторы или оставляют изолирующие участки. Каждый имеющийся или отсутствующий транзистор обозначает один бит. При активации шины выборки все транзисторы в этом столбце открываются, притягивая вниз соответствующие выходные шины. Но если в выбранной позиции транзистора нет, соответствующий выход останется высоким. Таким образом, значение читается из ПЗУ путём активации шины выборки, которая выдаёт это значение из ПЗУ на выходные шины.
Содержимое ПЗУ
ПЗУ с константами состоит из 143 рядов и 21 столбца. Он содержит 134 ряда по 21 биту, кроме одного кусочка 6×6 транзисторов слева вверху. Поэтому физический размер ПЗУ с константами составляет 2946 бит.

Исходя из схемы ПЗУ, отсутствующая секция означает, что первые 12 констант 64-битные, а не 67-битные. Это константы, не относящиеся к CORDIC, и им, видимо, не требуется дополнительная точность.
Под микроскопом видна схема битов ПЗУ, поэтому её можно оттуда извлечь. Однако совершенно неочевидно, как эти биты потом интерпретировать. Первый вопрос – обозначает ли наличие транзистора 0 или 1 (позже оказалось, что наличие транзистора – это 1). Вторая проблема – как перевести сетку битов 134×21 в значения.
Кодирование битов можно определить двумя способами. Первый – отследить схему, читающую данные из ПЗУ и посмотреть, как они используются. Второй – искать закономерности в сырых данных и попытаться их осмыслить. Поскольку 8087 очень сложный, я хотел избежать полного реверс-инжиниринга при изучении констант, поэтому я использовал второй подход.
Путь передачи данных чипа состоит из 67 горизонтальных рядов, поэтому было ясно, что 134 ряда в ПЗУ соответствуют двум наборам 67-битных констант. Я извлёк один набор констант из нечётных рядов, а другой – из чётных, однако полученные значения не имели смысла. Подумав ещё немного, я понял, что ряды не чередовались, а шли в повторяющемся порядке ABBA.
Ряды шли в порядке ABBAABBAABBA…, где в рядах А содержались биты для одного набора констант, а в рядах В – для другого. Такая схема использовалась вместо простого чередования АВАВ, возможно, потому, что один контакт может управлять двумя соседними транзисторами. То есть, один проводник может выбрать каждую из групп АА и ВВ.
Когда я учёл порядок АВВА, я получил кучу знакомых констант, включая π и 1. На диаграмме ниже показаны биты из этих констант. На фото бит 1 – зелёная полоска, бит 0 – красная. В двоичной системе π равно 11,001001..., и именно это значение видно в верхнем ряду размеченных битов. Нижнее значение – это константа 1.

Верхний ряд битов – число π, нижний – 1. Эта диаграмма повёрнута на 90° по сравнению с остальными.
Следующая сложность с интерпретацией состоит в том, что в ПЗУ хранятся только мантиссы, но не экспоненты (пока что я не нашёл отдельный ПЗУ с экспонентами). И я экспериментировал с различными экспонентами, пока не получал осмысленных значений. Некоторые были понятны сразу: к примеру, константа 1,204120 даёт log10 (2) с использованием экспоненты 2-2. Другие понять было посложнее, например, 1,734723. В итоге, я понял, что 1,734723×259 = 1018. Зачем в 8087 содержится такая константа? Возможно потому, что 8087 поддерживает упакованный двоично-десятичный код с 18 знаками.
Некоторые экспоненты было очень трудно найти, и я использовал метод перебора, чтобы посмотреть, не выдаст ли результат какой-нибудь логарифм или степень какого-то числа. Сложнее всего было определить константу для ln(2)/3. Важность этого числа мне непонятна.
Вот полный список констант из ПЗУ. Столбец «смысл» – это моё описание значения.
| Константы | Десятичное значение | Смысл |
|---|---|---|
| 1.204120×2-2 | 0.3010300 | log10 (2) |
| 1.386294×2-1 | 0.6931472 | ln(2) |
| 1.442695×20 | 1.426950 | log2 (e) |
| 1.570796×21 | 3.415927 | π |
| 1.000000×20 | 1.000000 | 1 |
| 1.660964×21 | 3.219281 | log2 (10) |
| 1.734723×259 | 1.00e+18 | 1018 |
| 1.734723×259 | 1.00e+18 | 1018 |
| 1.848392×2-3 | 0.2310491 | ln(2)/3 |
| 1.082021×22 | 4.280851 | 3*log2(e) |
| 1.442695×20 | 1.426950 | log2 (e) |
| 1.414214×20 | 1.142136 | √2 |
| 1.570796×2-1 | 0.7853982 | atan(20) |
| 1.854590×2-2 | 0.4636476 | atan(2-1) |
| 2.000000×2-15 | 0.0000610 | atan(2-14) |
| 2.000000×2-16 | 0.0000305 | atan(2-15) |
| 1.959829×2-3 | 0.2449787 | atan(2-2) |
| 1.989680×2-4 | 0.1243550 | atan(2-3) |
| 2.000000×2-13 | 0.0002441 | atan(2-12) |
| 2.000000×2-14 | 0.0001221 | atan(2-13) |
| 1.997402×2-5 | 0.0624188 | atan(2-4) |
| 1.999349×2-6 | 0.0312398 | atan(2-5) |
| 1.999999×2-11 | 0.0009766 | atan(2-10) |
| 2.000000×2-12 | 0.0004883 | atan(2-11) |
| 1.999837×2-7 | 0.0156237 | atan(2-6) |
| 1.999959×2-8 | 0.0078123 | atan(2-7) |
| 1.999990×2-9 | 0.0039062 | atan(2-8) |
| 1.999997×2-10 | 0.0019531 | atan(2-9) |
| 1.441288×2-9 | 0.0028150 | log2(1+2-9) |
| 1.439885×2-8 | 0.0056245 | log2(1+2-8) |
| 1.437089×2-7 | 0.0112273 | log2(1+2-7) |
| 1.431540×2-6 | 0.0223678 | log2(1+2-6) |
| 1.442343×2-11 | 0.0007043 | log2(1+2-11) |
| 1.441991×2-10 | 0.0014082 | log2(1+2-10) |
| 1.420612×2-5 | 0.0443941 | log2(1+2-5) |
| 1.399405×2-4 | 0.0874628 | log2(1+2-4) |
| 1.442607×2-13 | 0.0001761 | log2(1+2-13) |
| 1.442519×2-12 | 0.0003522 | log2(1+2-12) |
| 1.359400×2-3 | 0.1699250 | log2(1+2-3) |
| 1.287712×2-2 | 0.3219281 | log2(1+2-2) |
| 1.442673×2-15 | 0.0000440 | log2(1+2-15) |
| 1.442651×2-14 | 0.0000881 | log2(1+2-14) |
Не уверен, почему 1018 повторяется – возможно, отличие в экспоненте.
Физически константы расположены тремя группами. Первая группа – это значения, которые пользователь может загружать (1, π, log210, log2e, log102, и ln), а также значения для внутреннего использования (1018, ln(2)/3, 3*log2(e), log2(e) и √2). Вторая группа состоит из 16 констант арктангенса, а третья – из 14 констант log2.
В 8087 есть семь инструкций для прямой загрузки констант. Инструкции FDLZ, FLD1, FLDPI, FLD2T, FLD2E, FLDLG2 и FLDLN2 загружают в стек константы 0, 1, π, log210, log2e, log102 и ln 2 соответственно. Все эти константы кроме 0 хранятся в ПЗУ.
Последние две группы констант используются для подсчёта трансцендентных функций по алгоритмам CORDIC.
Алгоритмы CORDIC
По константам из ПЗУ можно узнать о некоторых деталях работы алгоритмов 8087. В ПЗУ содержится 16 значений для арктангенса, арктангенсы от 2-n. Также там хранится 14 логарифмов по основанию 2 от (1+2-n). Такие значения могут показаться необычными, однако они используются в эффективном алгоритме CORDIC, изобретённом в 1958 году.
Идея CORDIC состоит в том, что вычислить тангенс и арктангенс можно через разбиение угла на меньшие с поворотом вектора на эти углы. Фокус в том, что если правильно выбирать меньшие углы, то каждый поворот можно будет вычислить через эффективные сдвиги и сложения вместо тригонометрических функций. Допустим, нам нужно найти find tan(z). Мы можем разбить z на сумму небольших углов: z ≈ {atan(2-1) or 0} + {atan(2-2) or 0} + {atan(2-3) or 0} +… + {atan(2-16 or 0}. Поворачивать вектор, допустим, на atan(2-2) можно, умножая на 2-2 и складывая. Суть в том, что умножение на 2-2 осуществляется через быстрый побитовый сдвиг. Учитывая всё это, вычислить tan(z) можно, сравнивая z с константами atan, а потом пройдя 16 циклов сложений и сдвигов, что на железе делается быстро. Поэтому константы для atan предварительно подсчитаны и хранятся в ПЗУ. Арктангенс вычисляется сходным образом, только наоборот – в процессе поворотов углы (из ПЗУ с константами) суммируются и дают итоговый.
При вычислении логарифма и экспоненты также используются алгоритмы CORDIC и соответствующие им логарифмические константы. Главное тут то, что умножение на (1 + 2-n) можно делать быстро при помощи сдвигов и сложений. Логарифм и экспоненту можно вычислить, умножая одну сторону уравнения на последовательность значений и добавляя соответствующие логарифмические константы к другой. По алгоритмам вычисления логарифма и экспоненты документации для 8087 я не нашёл. Думаю, что они похожи на те, что описаны в следующей статье, только 8087 использует основание 2 вместо е. Не пойму, почему у 8087 нет константы log2 (1 + 2-1), необходимой для того алгоритма.
Поддержка трансцендентных функций в 8087 не такая уж и обширная, как можно было ожидать. Он поддерживает только тангенс и арктангенс, без синусов и косинусов. Для вычисления последних придётся применять тригонометрические тождества. Логарифмы и экспоненты поддерживают только основание 2 – для оснований 10 или е пользователю придётся применять масштабный коэффициент. В своё время 8087 расширил пределы ёмкости чипов, поэтому количество инструкций было сведено к минимуму.
Заключение
8087 – это сложный чип, и на первый взгляд похож на безнадёжно запутанный лабиринт. Однако по большей части в нём можно разобраться после тщательного изучения. В его ПЗУ хранится 42 константы, и их значения можно извлечь при помощи микроскопа. Некоторые константы (например, π) были ожидаемы, другие же (например, ln(2)/3) вызывают больше вопросов. Многие из констант используются для вычисления тангенсов, арктангенсов, логарифмов и степеней при помощи алгоритмов CORDIC.

Фото кристалла 8087 без металлического слоя. Кликабельно.
Хотя Intel 8087 для работы с плавающей запятой представили 40 лет назад, его влияние ощущается до сих пор. Он породил стандарт IEEE 754 для чисел с плавающей запятой, используемый в большей части арифметических вычислений, а инструкции 8087 остаются частью процессоров х86, используемых в большинстве компьютеров.