Практически в любой современной компьютерной игре наличие какого-либо физического движка является обязательным условием. Развевающиеся на ветру флаги и кролики, бомбардируемые шарами, ― всё это требует надлежащего исполнения. И, конечно, пусть не все герои носят плащи… но те, кто носят, действительно нуждаются в наличии адекватной симуляции развевающейся ткани.

И всё же полное физическое моделирование таких взаимодействий часто становится невозможным, поскольку оно на порядки медленнее необходимого для игр в реальном времени. Данная статья предлагает новый метод моделирования, который может ускорить физические симуляции, сделать их в 300-5000 раз быстрее. Цель его состоит в том, чтобы попытаться научить имитации физических сил нейронную сеть.
Прогресс в развитии физических движков обуславливается как растущей вычислительной мощностью технического оборудования, так и разработкой быстрых и стабильных методов моделирования. К таким методам относятся, например, моделирование путём нарезания пространства на подпространства и data-driven подходы ― то есть, на основе данных. Первые работают только в уменьшенном или сжатом подпространстве, где учитываются лишь немногие формы деформации. Для крупных проектов это может привести к значительному повышению технических требований. Data-driven подходы используют память системы и хранящиеся в ней предварительно вычисленные данные, что позволяет снизить эти самые требования.
Здесь мы рассмотрим подход, сочетающий в себе оба метода: таким образом предполагается извлечь выгоду из сильных сторон того и другого. Такой метод можно трактовать двумя способами: либо как метод моделирования подпространства, параметризованный нейросетью, либо как DD-метод, опирающийся на моделирование подпространства для построения сжатой моделируемой среды.
Его суть такая: сначала мы собираем высокоточные данные моделирования при помощи Maya nCloth, а затем производим вычисление линейного подпространства с помощью метода главных компонент (PCA). На следующем шаге мы задействуем машинное обучение на основе классической нейросетевой модели и нашей новой методики, после чего внедряем обученную модель в интерактивный алгоритм с несколькими оптимизациями, такими как эффективный алгоритм декомпрессии графическим процессором и метод аппроксимации нормалей вершин.
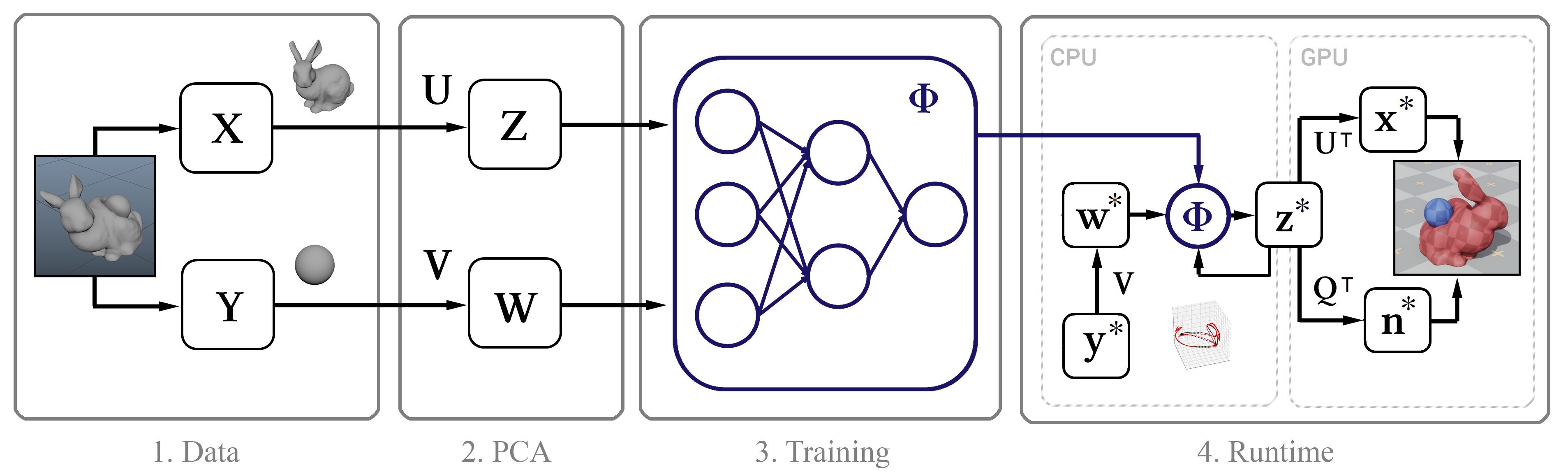
Рисунок 1. Структурная схема метода
Вообще говоря, единственными входными данными для этого метода являются необработанные временные метки покадровых позиций вершин объекта. Далее опишем процесс сбора таких данных.
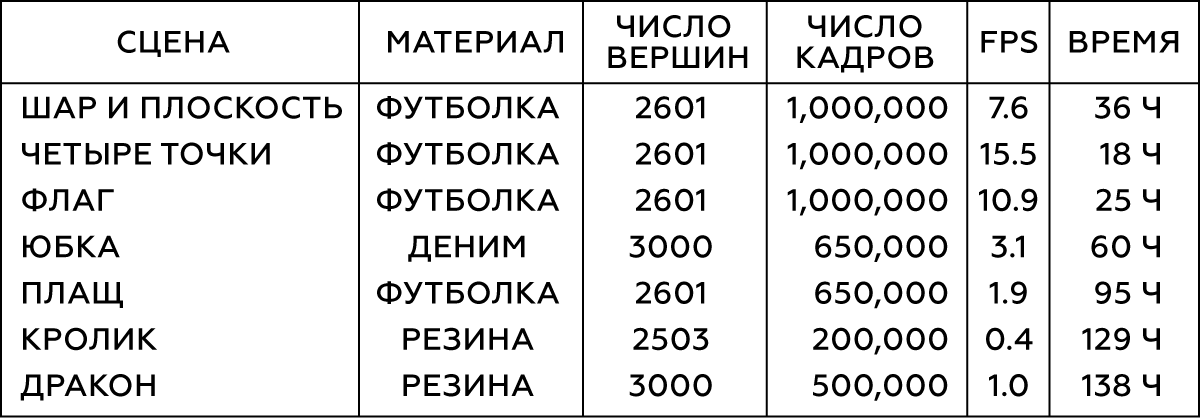
Моделирование выполним в Maya nCloth, захватывая данные со скоростью 60 кадров в секунду, с 5 или 20 подшагами и 10 или 25 ограничивающими итерациями ― в зависимости от стабильности моделирования. Для тканей возьмём модель футболки с небольшим увеличением веса материала и его сопротивления растяжению, а для деформируемых объектов ― твёрдую резину с уменьшенным трением. Внешние столкновения выполним путём столкновения треугольников внешней геометрии, самостолкновения ― вершин с вершинами для ткани и треугольников с треугольниками для резины. Во всех случаях мы используем довольно большую толщину столкновения ― порядка 5 см ― для обеспечения стабильности модели и предотвращения защемления и разрыва ткани.
Таблица 1. Параметры моделируемых объектов
Для различных видов взаимодействия простых объектов (например, сфер) сгенерируем их движение случайным образом путём кадрирования случайных координат в случайные же моменты времени. Для моделирования взаимодействия ткани с персонажем используем базу данных захвата движения из 6.5 × 105 кадров, представляющих собой одну большую анимацию. По завершении моделирования проверим результат и исключим кадры с нестабильным или плохим поведением. Для сцены с юбкой уберём руки персонажа, поскольку они часто пересекаются с геометрией сетки ног и сейчас являются несущественными.

Рисунок 2. Те самые две первые сцены из таблицы
Обычно нам нужно 105-106 кадров обучающих данных. По нашему опыту, в большинстве случаев 105 кадров оказывается достаточно для тестирования, в то время как лучшие результаты достигаются с 106 кадрами.
Далее поговорим о процессе машинного обучения: о параметризации в нашей нейросети, о сетевой архитектуре и непосредственно о самой методике.
Для того, чтобы получить обучающий набор данных, соберём координаты вершин в каждом кадре t в один вектор xt, а затем эти покадровые векторы объединим в одну большую матрицу X. Эта матрица описывает состояния моделируемого объекта. Помимо этого, мы должны иметь представление о состоянии внешних объектов в каждом кадре. Для простых объектов (таких как шары) можно использовать их трёхмерные координаты, в то время как состояние сложных моделей (персонаж) описывается положением каждого сустава относительно опорной точки: в случае юбки такой опорой будет тазобедренный сустав, в случае плаща ― шея. Для объектов с движущейся системой отсчета следует учитывать положение Земли относительно неё: тогда наша система будет знать направление силы тяжести, а также свои линейную скорость, ускорение, скорость вращения и ускорение вращения. Для флага будем учитывать скорость и направление ветра. В результате для каждого объекта получаем один большой вектор, описывающий состояние внешнего объекта, и все эти векторы тоже объединим в матрицу Y.
Теперь применим PCA как к матрице X, так и к Y, и используем получившиеся матрицы преобразования Z и W для построения изображения подпространства. Если процедура PCA требует слишком большого объёма памяти, сначала дискретизируем наши данные.
Сжатие при помощи PCA неизбежно приводит к потере детализации, особенно для объектов со многими потенциальными состояниями, таких как тонкие складки ткани. Однако, если подпространство состоит из 256 базовых векторов, это обычно помогает сохранить большинство деталей. Ниже представлены анимации эталонной физики плаща и моделей с 256, 128 и 64 базовыми векторами, соответственно.

Рисунок 3. Сравнение контрольной модели (эталона) с моделями, полученными по нашему методу в пространствах с различной размерностью базисов
Необходимо было разработать такую модель, которая могла бы предсказывать состояния векторов моделей в будущих кадрах. И поскольку моделируемым объектам обычно свойственна инерция с тенденцией к некоторому среднему состоянию покоя (после процедуры PCA такое состояние объект принимает при нулевых значениях), хорошей исходной моделью будет являться выражение, представленное строкой 9 алгоритма на рисунке 4. Здесь α и β ― параметры модели, ⊙ ― покомпонентное произведение. Значения этих параметров получим из исходных данных, решая линейное уравнение наименьших квадратов индивидуально для α и β:
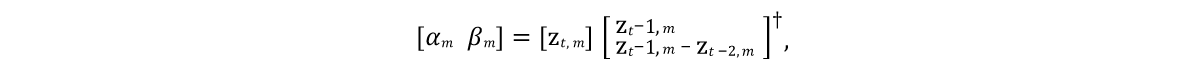
Здесь † ― псевдообратное преобразование матрицы.
Поскольку такое предсказание является лишь очень грубым приближением и не учитывает влияния внешних объектов w, очевидно, оно не сможет точно смоделировать обучающие данные. Поэтому обучим нейронную сеть Φ аппроксимации остаточных эффектов модели в соответствии с 11-ой строкой алгоритма. Здесь мы параметризуем стандартную нейронную сеть прямого распространения с 10 слоями, для каждого слоя (кроме выходного) применяя функцию активации ReLU. Исключив входной и выходной слои, мы установили количество скрытых единиц на каждом оставшемся слое равным полуторному размеру данных PCA, что привело к хорошему компромиссу между занимаемым местом на жёстком диске и производительностью.

Рисунок 4. Алгоритм обучения нейросети
Стандартный способ обучения нейросети состоял бы в том, чтобы перебрать весь набор данных и обучить сеть производить предсказания для каждого кадра. Конечно, подобный подход приведёт к низкой ошибке обучения, но обратная связь в таком предсказании вызовет нестабильное поведение его результата. Поэтому, чтобы обеспечить стабильное долгосрочное предсказание, наш алгоритм использует метод обратного распространения ошибки на протяжении всей процедуры интегрирования.
В целом он работает так: из небольшого окна обучающих данных z и w мы берём два первых кадра z0 и z1 и добавляем к ним небольшой шум r0, r1, чтобы слегка нарушить траекторию обучения. Затем для предсказания следующих кадров несколько раз прогоняем алгоритм, возвращаясь к предыдущим результатам предсказаний на каждом новом временном шаге. Как только получим предсказание всей траектории, вычислим среднюю ошибку координат, а затем передадим её оптимизатору AmsGrad, используя автоматические производные, вычисленные с помощью TensorFlow.
Будем повторять этот алгоритм на мини-выборках из 16 кадров, используя перекрывающиеся окна размером 32 кадра, на протяжении 100 эпох или до тех пор, пока обучение не сойдётся. Используем при этом скорость обучения 0.0001, коэффициент затухания скорости обучения 0.999 и стандартное отклонение шума, вычисленное по первым трём компонентам пространства PCA. Такое обучение занимает от 10 до 48 часов в зависимости от сложности установки и размера данных PCA.

Рисунок 5. Наглядное сравнение эталонной юбки и той, что научилась строить наша нейросеть
Подробно опишем реализацию нашего метода в интерактивной среде, включая оценку нейронной сети, вычисление нормалей к поверхностям объектов для рендеринга и то, как мы боремся с видимыми пересечениями.
Полученные модели мы рендерим в простом интерактивном 3D-приложении, написанном на C++ и DirectX: ещё раз реализуем предпроцессы и нейросетевые операции в однопоточном коде C++ и загрузим двоичные веса сети, полученные в ходе нашей процедуры обучения. Затем применим некоторые простые оптимизации для оценки сети, в частности ― повторное использование буферов памяти и разреженных векторно-матричных данных, что становится возможным из-за наличия нулевых скрытых единиц, полученных благодаря функции активации ReLU.
Отправим сжатые данные z о состояниях ткани на графический процессор и выполним их декомпрессию для дальнейшего рендеринга. С этой целью используем простой вычислительный шейдер, который для каждой вершины объекта вычисляет точечное произведение вектора z и первых трёх строк матрицы UT, соответствующих координатам этой вершины, после чего добавим среднее значение xµ. Этот подход имеет два преимущества перед наивным методом декомпрессии. Во-первых, параллелизм графического процессора значительно ускоряет вычисление вектора состояний модели, которое может занять до 1 мс. Во-вторых, он уменьшает время передачи данных между центральным и графическим процессором на порядок, что особенно важно для платформ, на которых передача всего состояния объекта целиком оказывается слишком медленной.
Во время рендеринга недостаточно иметь доступ только к координатам вершин ― необходима также информация о деформациях их нормалей. Обычно в физическом движке либо опускают это вычисление, либо выполняют наивный покадровый пересчет нормалей с последующим перераспределением их на соседние вершины. Это может оказаться неэффективным, потому как базовая реализация центрального процессора, в дополнение к затратам на декомпрессию и передачу данных, требует на такую процедуру еще порядка 150 мкс. И хотя это вычисление можно выполнить на графическом процессоре, реализовать его оказывается сложнее ввиду необходимости параллельных операций.
Вместо этого на вычислительном шейдере графического процессора выполним линейную регрессию состояния подпространства до нормальных векторов полного состояния. Зная значения нормалей вершин в каждом кадре, вычислим матрицу Q, которая наилучшим образом отображает представление подпространства на нормали вершин.
Поскольку предсказание нормалей в нашем методе до этого нигде не фигурировало, нет никакой гарантии, что такой подход окажется точным, однако на практике он показал себя действительно хорошо, в чём можно убедиться по рисунку ниже.

Рисунок 6. Сравнение моделей, вычисленных по нашему методу и эталонному (ground truth), а так же разница между ними
Наша нейросеть учится эффективно выполнять столкновения, однако из-за неточностей предсказаний и ошибок, вызванных сжатием подпространства, могут возникнуть пересечения между внешними объектами и смоделированными. Более того, поскольку мы откладываем вычисление полного состояния сцены до самого начала рендеринга, не остаётся возможности эффективно разрешить эти проблемы заранее. Поэтому для поддержания высокой производительности устранить эти пересечения необходимо во время рендеринга.
Мы нашли для этого простое и эффективное решение, заключающееся в том, что пересекающиеся вершины проецируются на поверхность примитивов, из которых мы составляем персонажа. Такое проецирование легко произвести на графическом процессоре с помощью того же вычислительного шейдера, что производит декомпрессию ткани и вычисляет нормали затенения.
Итак, в первую очередь составим персонажа из связанных с вершинами прокси-объектов с различными начальными и конечными радиусами, после чего передадим информацию о координатах и радиусах этих объектов в вычислительный шейдер. Ещё раз проверим координаты каждой вершины на предмет пересечения с соответствующим прокси-объектом и, если оно есть, спроецируем эту вершину на поверхность прокси-объекта. Так мы корректируем только положение вершины, не трогая саму нормаль, чтобы не повредить затенение.
Такой подход удалит небольшие видимые пересечения объектов при условии, что ошибки смещения вершин не настолько велики, чтобы проекция оказалась на противоположной стороне соответствующего прокси-объекта.

Рисунок 7. Модель персонажа, составленная из прокси-объектов, и результаты устранения видимых пересечений по нашему методу: до и после
Итак, наши тестовые сцены включают:
Во всех примерах наш метод задает природу деформаций, близкую к естественной.
Также мы проводили стресс-тесты нашего метода на сценах с сотней кроликов и 16 персонажами, каждый из которых моделировался независимо при частоте кадров 120 и 240 кадров в секунду.

Рисунок 8. Тест на 16 персонажах. Party time!
Итак, по приведённым в тексте иллюстрациям можно убедиться, что, пусть при сжатии и аппроксимации теряются некоторые детали, результаты всё равно выглядят очень аутентичными реальности.
Ниже показаны траектории, построенные на основе предсказаний состояний первых трёх базисных векторов PCA. По рисункам видно, что даже когда наш метод не совсем точен, он все ещё производит движения аналогичной формы и с теми же временными профилями, что и эталон.

Рисунок 9. Чёрным показаны траектории, построенные по нашему методу, красным – эталонные
Одним из ключевых преимуществ нашего метода является его производительность ― как в скорости выполнения операций, так и в использовании памяти. В таблице приведено сравнение нашего метода с другими известными, а также с контрольными данными. Наш метод достигает выигрыша в скорости порядка 300-5000 раз по сравнению с сырым моделированием, задающим эталонные данные. Он также имеет хорошую производительность по сравнению с другими современными методами, такими как метод гипер-редуцированной проективной динамики (HRPD), долгой краткосрочной памяти (LSTM) и управляемых рекуррентных блоков (GRU).
Сравниваемые структуры нейронных сетей спроектированы так, чтобы быть максимально похожими по размеру и занимаемому объёму памяти. Все измерения производительности выполнялись на однопоточном процессоре Intel Xeon E5-1650 3.5 GHz и графическом процессоре GeForce GTX 1080 Titan.
Таблица 2. Сравнение различных методов моделирования
Итак, наш метод генерирует высококачественные результаты на несколько порядков быстрее, чем эталонное моделирование. Применимость к широкому набору поведений деформации, производительность и скромный объём занимаемой памяти делают его практичным для использования в современных играх и приложениях виртуальной реальности.
Как и все data-driven подходы, эта методика имеет ряд ограничений. Так, нет никакой гарантии, что она будет работать далеко за пределами обучающих данных, однако усечение количества входов и выходов системы до минимума и максимума, найденных в обучающих данных, оказалось эффективным для борьбы с этой проблемой. Кроме того, все внешние объекты должны быть параметризованы, что в некоторых случаях может быть затруднено ― например, при меняющемся количестве этих самых внешних объектов.
Как и все подпространственные методы, этот метод ограничен размерностью базиса подпространства, и если её увеличение не помогает захватить мелкие детали, это становится возможным только при значительном увеличении вычислительных затрат.
Метод требует большого количества времени для сбора обучающих данных, а затем до нескольких дней моделирования. Как и в случае любого data-driven подхода, он требует надлежащего контроля ― например, удаления любых ошибочных данных из обучающего набора. С этой проблемой пока не получилось ничего сделать, но можно предположить, что процесс получится ускорить, если просто запустить несколько симуляций параллельно. Конвергентное время обучения для этого метода достаточно длительное, и, хотя первые результаты для тестирования могут быть готовы через час или два, окончательным моделям нейросеть учится приблизительно за день.
Без дополнительных решений метод не может гарантировать, что с внешней геометрией не будет происходить никаких пересечений. То же самое можно сказать и про самостолкновения.
Пока подход тестировался только на упругих объектах, но, вероятно, его можно распространить и на гибкие. Один из вариантов, как этого добиться, ― чётко отслеживать состояние покоя, предсказывая его изменение при помощи нейронной сети. По-видимому, для таких объектов придётся пересмотреть процесс получения обучающих данных, поскольку нельзя ожидать, что в отсутствие каких-либо взаимодействий они вернутся в состояние покоя. Для борьбы с большим числом потенциальных состояний таких объектов может потребоваться подход с использованием адаптивных баз.
Наконец, в наших примерах показаны только те взаимодействия, в которых внешний объект закреплен на месте, и только те смоделированные объекты, система отсчета которых управляется извне. Можно устроить систему так, чтобы нейронная сеть предсказывала силы, приложенные к системе отсчета внешних объектов, что позволило бы им свободно перемещаться, ― а также дало бы возможность для взаимодействия незакрепленных предметов, таких как бросание на деформируемый объект коробок, способных сдвинуть его с места. Но тогда придется пересмотреть многие из описанных процессов.
Также на анимацию моделей можно посмотреть по ссылке.

Рисунок 10. Дракон vs чайник: choose your fighter

И всё же полное физическое моделирование таких взаимодействий часто становится невозможным, поскольку оно на порядки медленнее необходимого для игр в реальном времени. Данная статья предлагает новый метод моделирования, который может ускорить физические симуляции, сделать их в 300-5000 раз быстрее. Цель его состоит в том, чтобы попытаться научить имитации физических сил нейронную сеть.
Прогресс в развитии физических движков обуславливается как растущей вычислительной мощностью технического оборудования, так и разработкой быстрых и стабильных методов моделирования. К таким методам относятся, например, моделирование путём нарезания пространства на подпространства и data-driven подходы ― то есть, на основе данных. Первые работают только в уменьшенном или сжатом подпространстве, где учитываются лишь немногие формы деформации. Для крупных проектов это может привести к значительному повышению технических требований. Data-driven подходы используют память системы и хранящиеся в ней предварительно вычисленные данные, что позволяет снизить эти самые требования.
Здесь мы рассмотрим подход, сочетающий в себе оба метода: таким образом предполагается извлечь выгоду из сильных сторон того и другого. Такой метод можно трактовать двумя способами: либо как метод моделирования подпространства, параметризованный нейросетью, либо как DD-метод, опирающийся на моделирование подпространства для построения сжатой моделируемой среды.
Его суть такая: сначала мы собираем высокоточные данные моделирования при помощи Maya nCloth, а затем производим вычисление линейного подпространства с помощью метода главных компонент (PCA). На следующем шаге мы задействуем машинное обучение на основе классической нейросетевой модели и нашей новой методики, после чего внедряем обученную модель в интерактивный алгоритм с несколькими оптимизациями, такими как эффективный алгоритм декомпрессии графическим процессором и метод аппроксимации нормалей вершин.

Рисунок 1. Структурная схема метода
Обучающие данные
Вообще говоря, единственными входными данными для этого метода являются необработанные временные метки покадровых позиций вершин объекта. Далее опишем процесс сбора таких данных.
Моделирование выполним в Maya nCloth, захватывая данные со скоростью 60 кадров в секунду, с 5 или 20 подшагами и 10 или 25 ограничивающими итерациями ― в зависимости от стабильности моделирования. Для тканей возьмём модель футболки с небольшим увеличением веса материала и его сопротивления растяжению, а для деформируемых объектов ― твёрдую резину с уменьшенным трением. Внешние столкновения выполним путём столкновения треугольников внешней геометрии, самостолкновения ― вершин с вершинами для ткани и треугольников с треугольниками для резины. Во всех случаях мы используем довольно большую толщину столкновения ― порядка 5 см ― для обеспечения стабильности модели и предотвращения защемления и разрыва ткани.
Таблица 1. Параметры моделируемых объектов

Для различных видов взаимодействия простых объектов (например, сфер) сгенерируем их движение случайным образом путём кадрирования случайных координат в случайные же моменты времени. Для моделирования взаимодействия ткани с персонажем используем базу данных захвата движения из 6.5 × 105 кадров, представляющих собой одну большую анимацию. По завершении моделирования проверим результат и исключим кадры с нестабильным или плохим поведением. Для сцены с юбкой уберём руки персонажа, поскольку они часто пересекаются с геометрией сетки ног и сейчас являются несущественными.

Рисунок 2. Те самые две первые сцены из таблицы
Обычно нам нужно 105-106 кадров обучающих данных. По нашему опыту, в большинстве случаев 105 кадров оказывается достаточно для тестирования, в то время как лучшие результаты достигаются с 106 кадрами.
Обучение
Далее поговорим о процессе машинного обучения: о параметризации в нашей нейросети, о сетевой архитектуре и непосредственно о самой методике.
Параметризация
Для того, чтобы получить обучающий набор данных, соберём координаты вершин в каждом кадре t в один вектор xt, а затем эти покадровые векторы объединим в одну большую матрицу X. Эта матрица описывает состояния моделируемого объекта. Помимо этого, мы должны иметь представление о состоянии внешних объектов в каждом кадре. Для простых объектов (таких как шары) можно использовать их трёхмерные координаты, в то время как состояние сложных моделей (персонаж) описывается положением каждого сустава относительно опорной точки: в случае юбки такой опорой будет тазобедренный сустав, в случае плаща ― шея. Для объектов с движущейся системой отсчета следует учитывать положение Земли относительно неё: тогда наша система будет знать направление силы тяжести, а также свои линейную скорость, ускорение, скорость вращения и ускорение вращения. Для флага будем учитывать скорость и направление ветра. В результате для каждого объекта получаем один большой вектор, описывающий состояние внешнего объекта, и все эти векторы тоже объединим в матрицу Y.
Теперь применим PCA как к матрице X, так и к Y, и используем получившиеся матрицы преобразования Z и W для построения изображения подпространства. Если процедура PCA требует слишком большого объёма памяти, сначала дискретизируем наши данные.
Сжатие при помощи PCA неизбежно приводит к потере детализации, особенно для объектов со многими потенциальными состояниями, таких как тонкие складки ткани. Однако, если подпространство состоит из 256 базовых векторов, это обычно помогает сохранить большинство деталей. Ниже представлены анимации эталонной физики плаща и моделей с 256, 128 и 64 базовыми векторами, соответственно.

Рисунок 3. Сравнение контрольной модели (эталона) с моделями, полученными по нашему методу в пространствах с различной размерностью базисов
Исходная и расширенная модель
Необходимо было разработать такую модель, которая могла бы предсказывать состояния векторов моделей в будущих кадрах. И поскольку моделируемым объектам обычно свойственна инерция с тенденцией к некоторому среднему состоянию покоя (после процедуры PCA такое состояние объект принимает при нулевых значениях), хорошей исходной моделью будет являться выражение, представленное строкой 9 алгоритма на рисунке 4. Здесь α и β ― параметры модели, ⊙ ― покомпонентное произведение. Значения этих параметров получим из исходных данных, решая линейное уравнение наименьших квадратов индивидуально для α и β:
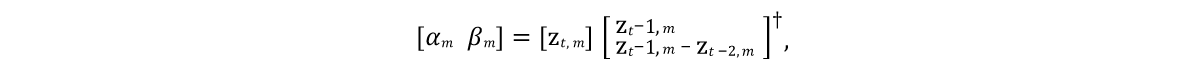
Здесь † ― псевдообратное преобразование матрицы.
Поскольку такое предсказание является лишь очень грубым приближением и не учитывает влияния внешних объектов w, очевидно, оно не сможет точно смоделировать обучающие данные. Поэтому обучим нейронную сеть Φ аппроксимации остаточных эффектов модели в соответствии с 11-ой строкой алгоритма. Здесь мы параметризуем стандартную нейронную сеть прямого распространения с 10 слоями, для каждого слоя (кроме выходного) применяя функцию активации ReLU. Исключив входной и выходной слои, мы установили количество скрытых единиц на каждом оставшемся слое равным полуторному размеру данных PCA, что привело к хорошему компромиссу между занимаемым местом на жёстком диске и производительностью.

Рисунок 4. Алгоритм обучения нейросети
Обучение нейтронной сети
Стандартный способ обучения нейросети состоял бы в том, чтобы перебрать весь набор данных и обучить сеть производить предсказания для каждого кадра. Конечно, подобный подход приведёт к низкой ошибке обучения, но обратная связь в таком предсказании вызовет нестабильное поведение его результата. Поэтому, чтобы обеспечить стабильное долгосрочное предсказание, наш алгоритм использует метод обратного распространения ошибки на протяжении всей процедуры интегрирования.
В целом он работает так: из небольшого окна обучающих данных z и w мы берём два первых кадра z0 и z1 и добавляем к ним небольшой шум r0, r1, чтобы слегка нарушить траекторию обучения. Затем для предсказания следующих кадров несколько раз прогоняем алгоритм, возвращаясь к предыдущим результатам предсказаний на каждом новом временном шаге. Как только получим предсказание всей траектории, вычислим среднюю ошибку координат, а затем передадим её оптимизатору AmsGrad, используя автоматические производные, вычисленные с помощью TensorFlow.
Будем повторять этот алгоритм на мини-выборках из 16 кадров, используя перекрывающиеся окна размером 32 кадра, на протяжении 100 эпох или до тех пор, пока обучение не сойдётся. Используем при этом скорость обучения 0.0001, коэффициент затухания скорости обучения 0.999 и стандартное отклонение шума, вычисленное по первым трём компонентам пространства PCA. Такое обучение занимает от 10 до 48 часов в зависимости от сложности установки и размера данных PCA.

Рисунок 5. Наглядное сравнение эталонной юбки и той, что научилась строить наша нейросеть
Реализация системы
Подробно опишем реализацию нашего метода в интерактивной среде, включая оценку нейронной сети, вычисление нормалей к поверхностям объектов для рендеринга и то, как мы боремся с видимыми пересечениями.
Приложение для рендеринга
Полученные модели мы рендерим в простом интерактивном 3D-приложении, написанном на C++ и DirectX: ещё раз реализуем предпроцессы и нейросетевые операции в однопоточном коде C++ и загрузим двоичные веса сети, полученные в ходе нашей процедуры обучения. Затем применим некоторые простые оптимизации для оценки сети, в частности ― повторное использование буферов памяти и разреженных векторно-матричных данных, что становится возможным из-за наличия нулевых скрытых единиц, полученных благодаря функции активации ReLU.
Декомпрессия с помощью графического процессора
Отправим сжатые данные z о состояниях ткани на графический процессор и выполним их декомпрессию для дальнейшего рендеринга. С этой целью используем простой вычислительный шейдер, который для каждой вершины объекта вычисляет точечное произведение вектора z и первых трёх строк матрицы UT, соответствующих координатам этой вершины, после чего добавим среднее значение xµ. Этот подход имеет два преимущества перед наивным методом декомпрессии. Во-первых, параллелизм графического процессора значительно ускоряет вычисление вектора состояний модели, которое может занять до 1 мс. Во-вторых, он уменьшает время передачи данных между центральным и графическим процессором на порядок, что особенно важно для платформ, на которых передача всего состояния объекта целиком оказывается слишком медленной.
Предсказание нормалей вершин
Во время рендеринга недостаточно иметь доступ только к координатам вершин ― необходима также информация о деформациях их нормалей. Обычно в физическом движке либо опускают это вычисление, либо выполняют наивный покадровый пересчет нормалей с последующим перераспределением их на соседние вершины. Это может оказаться неэффективным, потому как базовая реализация центрального процессора, в дополнение к затратам на декомпрессию и передачу данных, требует на такую процедуру еще порядка 150 мкс. И хотя это вычисление можно выполнить на графическом процессоре, реализовать его оказывается сложнее ввиду необходимости параллельных операций.
Вместо этого на вычислительном шейдере графического процессора выполним линейную регрессию состояния подпространства до нормальных векторов полного состояния. Зная значения нормалей вершин в каждом кадре, вычислим матрицу Q, которая наилучшим образом отображает представление подпространства на нормали вершин.
Поскольку предсказание нормалей в нашем методе до этого нигде не фигурировало, нет никакой гарантии, что такой подход окажется точным, однако на практике он показал себя действительно хорошо, в чём можно убедиться по рисунку ниже.

Рисунок 6. Сравнение моделей, вычисленных по нашему методу и эталонному (ground truth), а так же разница между ними
Борьба с пересечениями
Наша нейросеть учится эффективно выполнять столкновения, однако из-за неточностей предсказаний и ошибок, вызванных сжатием подпространства, могут возникнуть пересечения между внешними объектами и смоделированными. Более того, поскольку мы откладываем вычисление полного состояния сцены до самого начала рендеринга, не остаётся возможности эффективно разрешить эти проблемы заранее. Поэтому для поддержания высокой производительности устранить эти пересечения необходимо во время рендеринга.
Мы нашли для этого простое и эффективное решение, заключающееся в том, что пересекающиеся вершины проецируются на поверхность примитивов, из которых мы составляем персонажа. Такое проецирование легко произвести на графическом процессоре с помощью того же вычислительного шейдера, что производит декомпрессию ткани и вычисляет нормали затенения.
Итак, в первую очередь составим персонажа из связанных с вершинами прокси-объектов с различными начальными и конечными радиусами, после чего передадим информацию о координатах и радиусах этих объектов в вычислительный шейдер. Ещё раз проверим координаты каждой вершины на предмет пересечения с соответствующим прокси-объектом и, если оно есть, спроецируем эту вершину на поверхность прокси-объекта. Так мы корректируем только положение вершины, не трогая саму нормаль, чтобы не повредить затенение.
Такой подход удалит небольшие видимые пересечения объектов при условии, что ошибки смещения вершин не настолько велики, чтобы проекция оказалась на противоположной стороне соответствующего прокси-объекта.

Рисунок 7. Модель персонажа, составленная из прокси-объектов, и результаты устранения видимых пересечений по нашему методу: до и после
Анализ результатов
Итак, наши тестовые сцены включают:
- плоскость, взаимодействующую с управляемым пользователем шаром;
- плоскость, растянутую между четырьмя точками, которые пользователь может двигать;
- флаг, развевающийся на ветру;
- плащ и юбку на анимированном персонаже, управляемом пользователем;
- кролика, ударяемого управляемым пользователем шаром;
- дракона, по которому движется чайник.
Во всех примерах наш метод задает природу деформаций, близкую к естественной.
Также мы проводили стресс-тесты нашего метода на сценах с сотней кроликов и 16 персонажами, каждый из которых моделировался независимо при частоте кадров 120 и 240 кадров в секунду.

Рисунок 8. Тест на 16 персонажах. Party time!
Сравнение с эталоном
Итак, по приведённым в тексте иллюстрациям можно убедиться, что, пусть при сжатии и аппроксимации теряются некоторые детали, результаты всё равно выглядят очень аутентичными реальности.
Ниже показаны траектории, построенные на основе предсказаний состояний первых трёх базисных векторов PCA. По рисункам видно, что даже когда наш метод не совсем точен, он все ещё производит движения аналогичной формы и с теми же временными профилями, что и эталон.

Рисунок 9. Чёрным показаны траектории, построенные по нашему методу, красным – эталонные
Исполнение
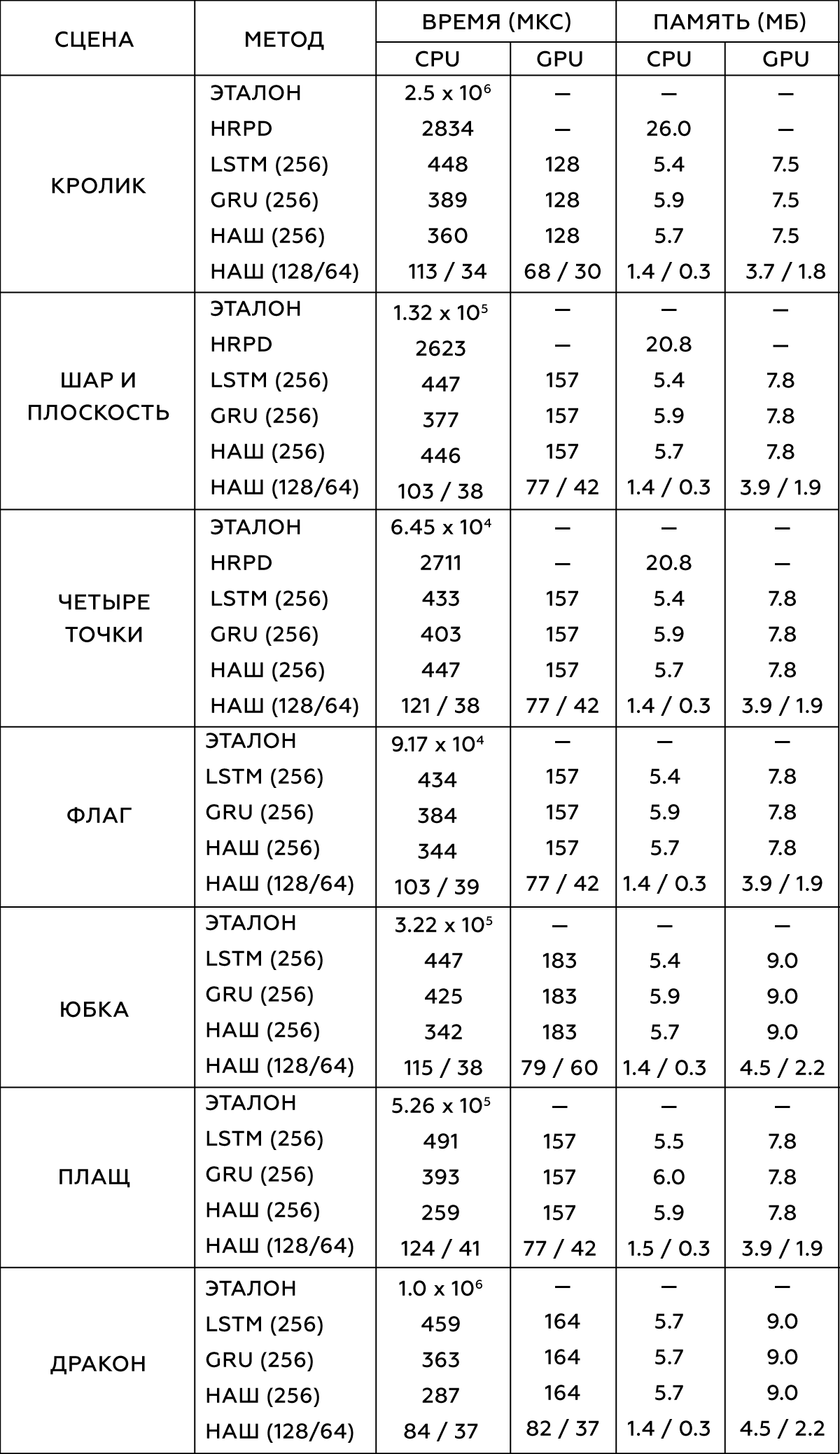
Одним из ключевых преимуществ нашего метода является его производительность ― как в скорости выполнения операций, так и в использовании памяти. В таблице приведено сравнение нашего метода с другими известными, а также с контрольными данными. Наш метод достигает выигрыша в скорости порядка 300-5000 раз по сравнению с сырым моделированием, задающим эталонные данные. Он также имеет хорошую производительность по сравнению с другими современными методами, такими как метод гипер-редуцированной проективной динамики (HRPD), долгой краткосрочной памяти (LSTM) и управляемых рекуррентных блоков (GRU).
Сравниваемые структуры нейронных сетей спроектированы так, чтобы быть максимально похожими по размеру и занимаемому объёму памяти. Все измерения производительности выполнялись на однопоточном процессоре Intel Xeon E5-1650 3.5 GHz и графическом процессоре GeForce GTX 1080 Titan.
Таблица 2. Сравнение различных методов моделирования

Ограничения метода и перспективы развития
Итак, наш метод генерирует высококачественные результаты на несколько порядков быстрее, чем эталонное моделирование. Применимость к широкому набору поведений деформации, производительность и скромный объём занимаемой памяти делают его практичным для использования в современных играх и приложениях виртуальной реальности.
Как и все data-driven подходы, эта методика имеет ряд ограничений. Так, нет никакой гарантии, что она будет работать далеко за пределами обучающих данных, однако усечение количества входов и выходов системы до минимума и максимума, найденных в обучающих данных, оказалось эффективным для борьбы с этой проблемой. Кроме того, все внешние объекты должны быть параметризованы, что в некоторых случаях может быть затруднено ― например, при меняющемся количестве этих самых внешних объектов.
Как и все подпространственные методы, этот метод ограничен размерностью базиса подпространства, и если её увеличение не помогает захватить мелкие детали, это становится возможным только при значительном увеличении вычислительных затрат.
Метод требует большого количества времени для сбора обучающих данных, а затем до нескольких дней моделирования. Как и в случае любого data-driven подхода, он требует надлежащего контроля ― например, удаления любых ошибочных данных из обучающего набора. С этой проблемой пока не получилось ничего сделать, но можно предположить, что процесс получится ускорить, если просто запустить несколько симуляций параллельно. Конвергентное время обучения для этого метода достаточно длительное, и, хотя первые результаты для тестирования могут быть готовы через час или два, окончательным моделям нейросеть учится приблизительно за день.
Без дополнительных решений метод не может гарантировать, что с внешней геометрией не будет происходить никаких пересечений. То же самое можно сказать и про самостолкновения.
Пока подход тестировался только на упругих объектах, но, вероятно, его можно распространить и на гибкие. Один из вариантов, как этого добиться, ― чётко отслеживать состояние покоя, предсказывая его изменение при помощи нейронной сети. По-видимому, для таких объектов придётся пересмотреть процесс получения обучающих данных, поскольку нельзя ожидать, что в отсутствие каких-либо взаимодействий они вернутся в состояние покоя. Для борьбы с большим числом потенциальных состояний таких объектов может потребоваться подход с использованием адаптивных баз.
Наконец, в наших примерах показаны только те взаимодействия, в которых внешний объект закреплен на месте, и только те смоделированные объекты, система отсчета которых управляется извне. Можно устроить систему так, чтобы нейронная сеть предсказывала силы, приложенные к системе отсчета внешних объектов, что позволило бы им свободно перемещаться, ― а также дало бы возможность для взаимодействия незакрепленных предметов, таких как бросание на деформируемый объект коробок, способных сдвинуть его с места. Но тогда придется пересмотреть многие из описанных процессов.
Также на анимацию моделей можно посмотреть по ссылке.

Рисунок 10. Дракон vs чайник: choose your fighter