Если вы погуглите ROC curve machine learning, то Википедия выдаст вам такой ответ: Кривая рабочих характеристик приёмника, или ROC-кривая, представляет собой график функции, который иллюстрирует диагностические возможности системы двоичного классификатора при изменении её порога распознавания.
Ещё одно частое описание ROC-кривой: ROC-кривая отражает чувствительность модели к разным порогам классификации. Новичков эти определения могут сбить с толку. Попробуем разобраться и развить представление о ROC-кривых.
Что за чертовщина эта ROC-кривая?
Вариант, как понять ROC-кривую: она описывает взаимосвязь между чувствительностью модели (TPR, или true positives rate — доля истинно положительных примеров) и её специфичностью (описываемой в отношении долей ложноположительных результатов: 1-FPR).
Давайте разовьём эту концепцию. TPR, или чувствительность модели, является соотношением корректных классификаций положительного класса, разделённых на все положительные классы, доступные из набора данных:
FPR — доля ложноположительных примеров, false positives rate. Это соотношение между ложными срабатываниями (количество прогнозов, ошибочно отнесённых в положительные), и всеми доступными отрицательными классами. Математически:
Обобщая: вы сравниваете, как чувствительность модели меняется по отношению к ложно положительным долям на разных порогах отсечения. Модель опирается на порог отсечения, чтобы принимать решения по входным данным и относить их к положительным.
Разделение проблемы с порогами отсечения
Поначалу интуиция толкала к пониманию роли порогов отсечения. Мне помогла мысленная картина:
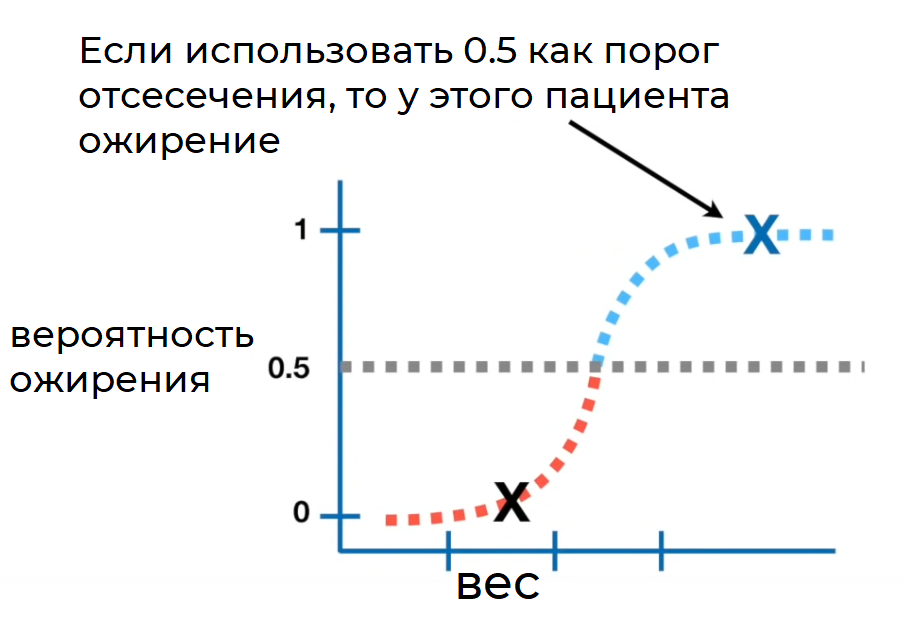
С такой классической визуализацией до меня дошло первое представление, а именно: идеальная модель — та, в которой доля истинно положительных результатов максимально высока, в то же время доля ложно положительных результатов удерживается как можно ниже.
Порог соответствует переменной T (например, значение между 0 и 1), служит границей принятия решения для классификатора и влияет на компромисс между TPR и FPR. Давайте напишем код, чтобы визуализировать все компоненты.
Визуализация ROC-кривой
Последовательность действий:
Импортировать зависимости
Сгенерировать данные с помощью drawdata для Jupyter
Импортировать сгенерированные данные в фреймворк pandas
Подобрать модель логистической регрессии к данным
Получить прогнозы модели логистической регрессии в виде значений вероятности
Установить другие пороги отсечения
Визуализировать ROC-кривую
Сделать окончательные выводы
Импортируем зависимости
from drawdata import draw_scatter
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, precision_recall_curve,precision_score, plot_roc_curveСгенерируем данные с помощью пакета drawdata для блокнотов Jupyter
draw_scatter()Что получается на выходе:

Импортируем данные в фреймворк pandas
df = pd.read_csv("./data.csv")Подберём модель логистической регрессии к данным
def get_fp_tp(y, proba, threshold):
"""Возвращает количество долей ложно положительных и истинно положительных."""
# источник: https://towardsdatascience.com/roc-curve-explained-50acab4f7bd8
# Разносим по классам
pred = pd.Series(np.where(proba>=threshold, 1, 0),
dtype='category')
pred.cat.set_categories([0,1], inplace=True)
# Создаём матрицу ошибок
confusion_matrix = pred.groupby([y, pred]).size().unstack()\
.rename(columns={0: 'pred_0',
1: 'pred_1'},
index={0: 'actual_0',
1: 'actual_1'})
false_positives = confusion_matrix.loc['actual_0', 'pred_1']
true_positives = confusion_matrix.loc['actual_1', 'pred_1']
return false_positives, true_positives
# train / test split на примере сгенерированного датасета
X = df[["x", "y"]].values
Y = df["z"].values
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
y_test = np.array([1 if p=="a" else 0 for p in y_test])
y_train = np.array([1 if p=="a" else 0 for p in y_train])
# создаём модель
lgr = LogisticRegression()
lgr.fit(X_train, y_train)Получим прогнозы модели логистической регрессии в виде значений вероятности
y_hat = lgr.predict_proba(X_test)[:,1]Установим другие пороговые значения
thresholds = np.linspace(0,1,100)Визуализируем ROC-кривую
# defining fpr and tpr
tpr = []
fpr = []
# определяем положительные и отрицательные
positives = np.sum(y_test==1)
negatives = np.sum(y_test==0)
# перебираем пороговые значения и получаем количество ложно и истинно положительных результатов
for th in thresholds:
fp,tp = get_fp_tp(y_test, y_hat, th)
tpr.append(tp/positives)
fpr.append(fp/negatives)
plt.plot([0, 1], [0, 1], linestyle='--', lw=2, color='r',label='Random', alpha=.8)
plt.plot(fpr,tpr, label="ROC Curve",color="blue")
plt.text(0.5, 0.5, "varying threshold scores (0-1)", rotation=0, size=12,ha="center", va="center",bbox=dict(boxstyle="rarrow"))
plt.xlabel("False Positve Rate")
plt.ylabel("True Positive Rate")
plt.legend()
plt.show()
Сделаем окончательные выводы
Изменяя порог, мы получили возрастающие значения как истинно положительных, так и ложно положительных долей. В хорошей модели порог отсечения ставит истинно положительные доли как можно ближе к 1, при этом сохраняя ложно положительные доли на самом нижнем из возможных уровней.
Как нам выбрать лучший порог?
Простой способ: выбрать тот порог, у которого максимальная сумма из истинно положительных и ложно отрицательных долей (1-FPR).
Другой критерий: простой выбор точки, ближайшей к левому верхнему углу ROC-кривой. Однако такой критерий подразумевает, что истинно положительный и истинно отрицательный показатели имеют одинаковый вес. В некоторых случаях, такая выборка не подходит, поскольку отрицательное влияние ложно положительных долей весомее, чем влияние истинно положительных.
Итоговые выводы о ROC-кривой
Я считаю, что в долгосрочной перспективе машинного обучения полезно потратить время на освоение оценочных показателей. В этой статье вы узнали:
Базовое представление о том, как работают ROC-кривые
Как пороги отсечения влияют на соотношение чувствительности и особенности модели
Как использовать ROC-кривые для выбора оптимальных порогов отсечения