Как разобраться с пауками в квантовой программе

Продолжаем рубрику тем для первого свидания. На сегодняшней повестке дня — упрощение схем для квантовых программ методами ZX-исчисления.

Далее от имени автора

Прежде всего, я хотел бы поблагодарить моих наставников Роджера Ло и Цзиньго Лю за то, что они курировали меня во время Google Summer of Code 2020. В этом проекте GSoC я разрабатываю новый пакет Julia ZXCalculus.jl, который реализует ZX-исчисление, и интегрирую его в качестве инструмента упрощения схем и квантовых программ в YaoLang.jl — DSL (предметно-ориентированный язык) для Yao.jl. Yao.jl — современный квантовый симулятор со множеством продвинутых функций, такими как автоматическое дифференцирование и символьные вычисления. Как пользователь "Yao.jl", я рад возможности внести свой вклад в его развитие. В этом блоге я подытожу результаты проделанной работы.

Квантовые схемы и ZX-исчисление

Квантовое программирование использует принципы квантовой механики для вычислений. Для описания квантовых алгоритмов мы часто используем модель квантовой схемы, которая является аналогом модели классической логической схемы. Квантовые схемы состоят из набора основных квантовых элементов, таких как вентили Паули, Адамара, T, CNOT.

В общем, будет много эквивалентных квантовых схем, представляющих одну и ту же операцию. С точки зрения квантового оборудования, нужно найти схему, которая минимизирует использование аппаратных ресурсов. К сожалению, поиск наиболее желаемой схемы является очень сложной задачей в плане вычислительной сложности, так как проверка эквивалентности между двумя квантовыми схемами является coQMA-трудной (квантовый аналог coNP) [1], [2]. Несмотря на это, у нас все еще есть некоторые эвристические эффективные алгоритмы для упрощения квантовых схем. В этом блоге я представлю мощный инструмент для этой проблемы — ZX-исчисление.

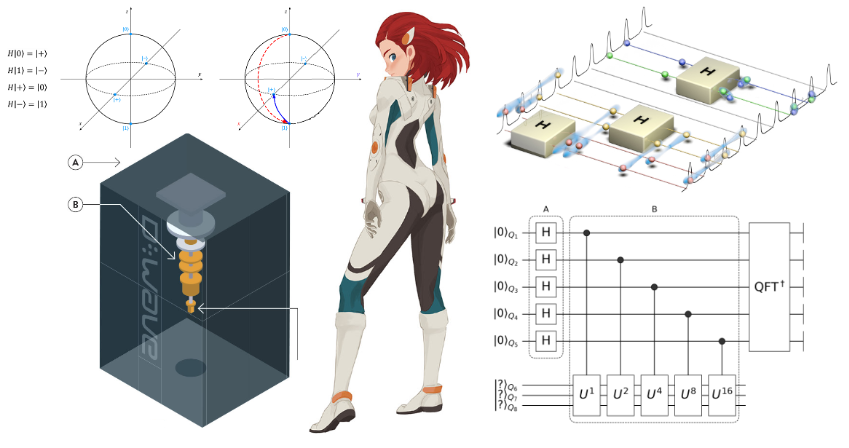
Квантовая схема — это граф, представляющий тензорные и матричные произведения. Например

Кроме того, квантовые схемы можно рассматривать как особый тип тензорной сети. В ZX-исчислении мы вводим два вида тензоров: Z-пауков и X-пауков. Тензорные сети, состоящие из этих тензоров, называются ZX-диаграммами. Поскольку все основные квантовые элементы могут быть представлены ZX-диаграммами, мы можем преобразовать все квантовые схемы в ZX-диаграммы.

Более того, по определению Z-пауков и X-пауков, существуют основные эквивалентные правила, с помощью которых можно упростить ZX-диаграммы.

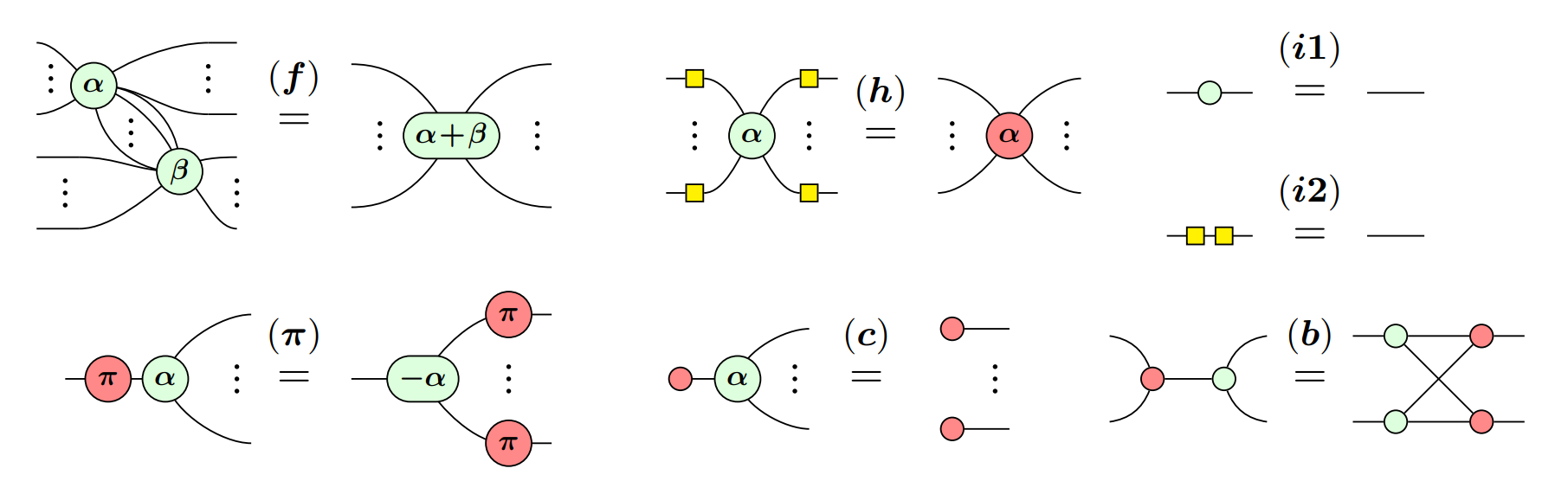
После упрощения ZX-диаграмм мы должны преобразовать их обратно в схемы. В работе [3] разработаны алгоритмы для приведенной выше схемы.

Во время GSoC 2020 я собираюсь добиться реализации на Джулии ZX-исчисления. В следующих разделах я кратко объясню причины и методы этого проекта.

Цель GSoC проекта

Основная цель этого проекта заключается в реализации ZX-исчисления и связанного с ним алгоритма на языке Julia. И мы выпустим пакет Julia ZXCalculus.jl. Существует Python-реализация ZX-исчисления, PyZX. Как и PyZX, ZXCalculus.jl должна предоставлять API для перевода на ZX-диаграммы, извлечения схем из ZX-диаграмм, упрощения и визуализации. Большинство функций PyZX будут реализованы в ZXCalculus.jl. Кроме того, мы интегрируем ZXCalculus.jl в квантовый компилятор YaoLang.jl и реализуем механизм упрощения схем на уровне компиляции.

В YaoLang.jl можно определить гибридные квантовые программы с классической информацией (например, классические параметры, классические потоки управления). Эти квантовые программы будут преобразованы в промежуточное представление (Yao IR), которое содержит квантовые схемы наряду с формой SSA (Статическая форма единого назначения) классической программы. Эти схемы будут упрощены с помощью ZXCalculus.jl. Затем YaoIR будет скомпилирован в бэкенд-инструкции, такие как QASM или инструкции симулятора Yao.

Для достижения наилучшей производительности при компиляции и обеспечения возможности дальнейшей настройки процедуры упрощения необходима чистая реализация ZX-исчисления на языке Julia.

Методы

Метод извлечения схем является каноническим методом алгоритмов упрощения схем на основе ZX-исчисления. Далее в основном будем обсуждать его реализацию.

Структуры данных

Для реализации этих алгоритмов нам необходимо реализовать структуры данных для хранения ZX-диаграмм и правила изменения ZX-диаграмм. ZX-диаграмму можно рассматривать как мультиграф с дополнительной информацией о его вершинах. Каждая вершина может быть представлена чем-то из Z-пауков, X-пауков или H-коробок. В исходных ZX-диаграммах допускаются открытые ребра. Для простоты мы добавили 2 специальных вида вершин, входную границу и выходную границу для записи этих ребер. Мы используем представление списка смежности для хранения мультиграфов. Список смежности хранится в виде "Dict", ключами которого являются идентификаторы вершин.

struct Multigraph{T<:Integer} <: AbstractMultigraph{T}
    adjlist::Dict{T, Vector{T}}
end

Поскольку нам нужно переписать мультиграфы с помощью правил ZX-исчисления, будет удобнее фиксировать идентификаторы вершин. Поэтому мы используем Dict вместо Array. Еще бывают фазы для Z- и X-пауков. Нам нужен еще один словарь для хранения этих фаз. Структура данных ZX-диаграммы аналогична следующей:

struct ZXDiagram{T<:Integer, P} <: AbstractZXDiagram{T, P}
    mg::Multigraph{T}
    st::Dict{T, SpiderType.SType}
    ps::Dict{T, P}
    ...
end

В статье предложены графоподобные ZX-диаграммы. Они включают в себя только Z-пауков и имеют разные типы граней: адамаровские и неадамаровские. Мы также можем использовать мультиграфы для представления графоподобных ZX-диаграмм и различные кратности ребер для представления различных типов ребер. Мы определяем ZXGraph для графоподобных ZX-диаграмм так:

struct ZXGraph{T<:Integer, P} <: AbstractZXDiagram{T, P}
    mg::Multigraph{T}
    st::Dict{T, SpiderType.SType}
    ps::Dict{T, P}
    ...
end

С этого момента мы создали структуры данных, которые нам нужны.

Правила преобразований

Чтобы упростить ZX-диаграммы, нам нужно реализовать правила перезаписи в ZX-исчислении. Существует два шага: сопоставление правил и переписывание ZX-диаграмм с соответствующими правилами. Мы использовали для этого благословенную джулианскую множественную диспетчеризацию. API-интерфейсы выглядят как-то так:

match(r::AbstractRule, zxd::AbstractZXDiagram)
rewrite!(r::AbstractRule, zxd::AbstractZXDiagram{T, P}, matches::Vector{Match{T}}) where {T, P}

Здесь match вернет все совпадающие вершины, которые будут сохранены в структуре

struct Match{T<:Integer}
    vertices::Vector{T}
end

А rewrite! — попытается использовать правило, чтобы переписать ZX-диаграмму на всех совпадающих вершинах. Так как некоторые совпадающие вершины могут стать неудовлетворяющими соответствующему правилу после переписывания некоторых вершин, нам нужно проверить, доступно ли еще правило для совпадающих вершин.

check_rule(r::AbstractRule, zxd::AbstractZXDiagram{T, P}, vs::Vector{T}) where {T, P}

Для упрощения ZX-диаграммы с помощью правила мы определили simplify! так:

function simplify!(r::AbstractRule, zxd::ZXDiagram)
    matches = match(r, zxd)
    while length(matches) > 0
        rewrite!(r, zxd, matches)
        matches = match(r, zxd)
    end
    return zxd
end

На этапе упрощения [3], мы должны конвертировать ZX-диаграмму в графоподобный вариант с правилами i1, i2, h, и f. После, упрощаем графоподобную ZX-диаграмму локальным дополнительным правилом и правилом замещения. Мы можем выполнить эти шаги с помощью вышеуказанных функций. Упрощенные графоподобные ZX-диаграммы будут просто маленькими скелетами по сравнению с первоначально большой схемой. Единственное, что остается — это извлечение схем из ZX-диаграмм.

Извлечение схем

Это самая сложная часть схемы упрощения. Для получения более подробной информации можно прочитать оригинал статьи. Я только кратко объясню алгоритм извлечения схемы.

Существует особенность для любой ZX-диаграммы квантовой схемы. Мы можем определить на ней g-поток. С помощью g-потока мы можем узнать порядок всех пауков. Правила, которые мы использовали для упрощения ZX-диаграммы, сохранят это хорошее свойство. Это дает нам возможность извлекать схемы из упрощенных ZX-диаграмм.

Кроме того, любая графоподобная ZX-диаграмма локально представима по CNOT + H. Мы можем извлечь эти схемы CNOT с гауссовским устранением над $F_2$. Вместе с остальными H-, CZ-гейтами и Z-вращениями мы получаем схему, эквивалентную исходной.

Demo

Демонстрационная схема взята из приложения к статье [3]. Все коды можно найти в разделе examples\ex1.jl у ZXCalculus.jl.

# this is the original circuit.
zxd = generate_example()
ZXplot(zxd)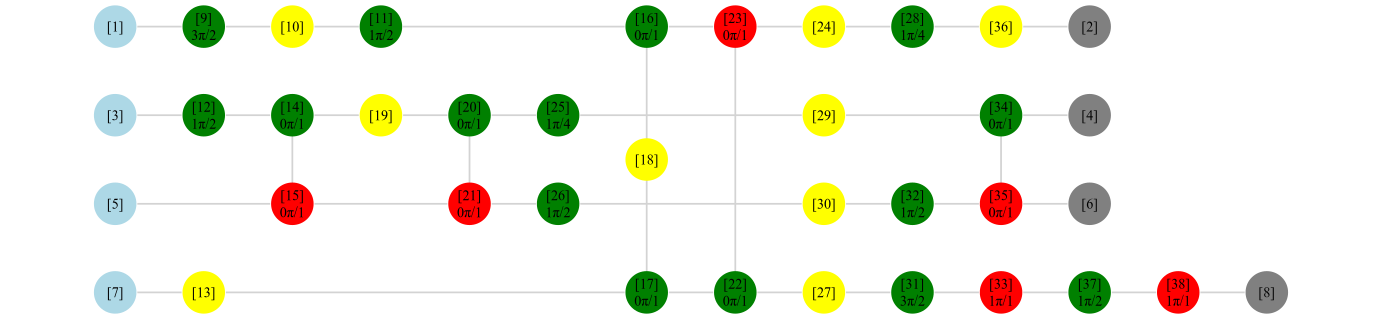

# convert a ZX-diagram to a graph-like ZXdiagram
zxg = ZXGraph(zxd)
ZXplot(zxg, linetype = "curve")

# simplify with local complementary rule 
simplify!(Rule{:lc}(), zxg)
ZXplot(zxg, linetype = "curve")

# simplify with pivoting rule
simplify!(Rule{:p1}(), zxg)
ZXplot(zxg, linetype = "curve")

# removing all Paulis adjancent to boundaries
replace!(Rule{:pab}(), zxg)
ZXplot(zxg, linetype = "curve")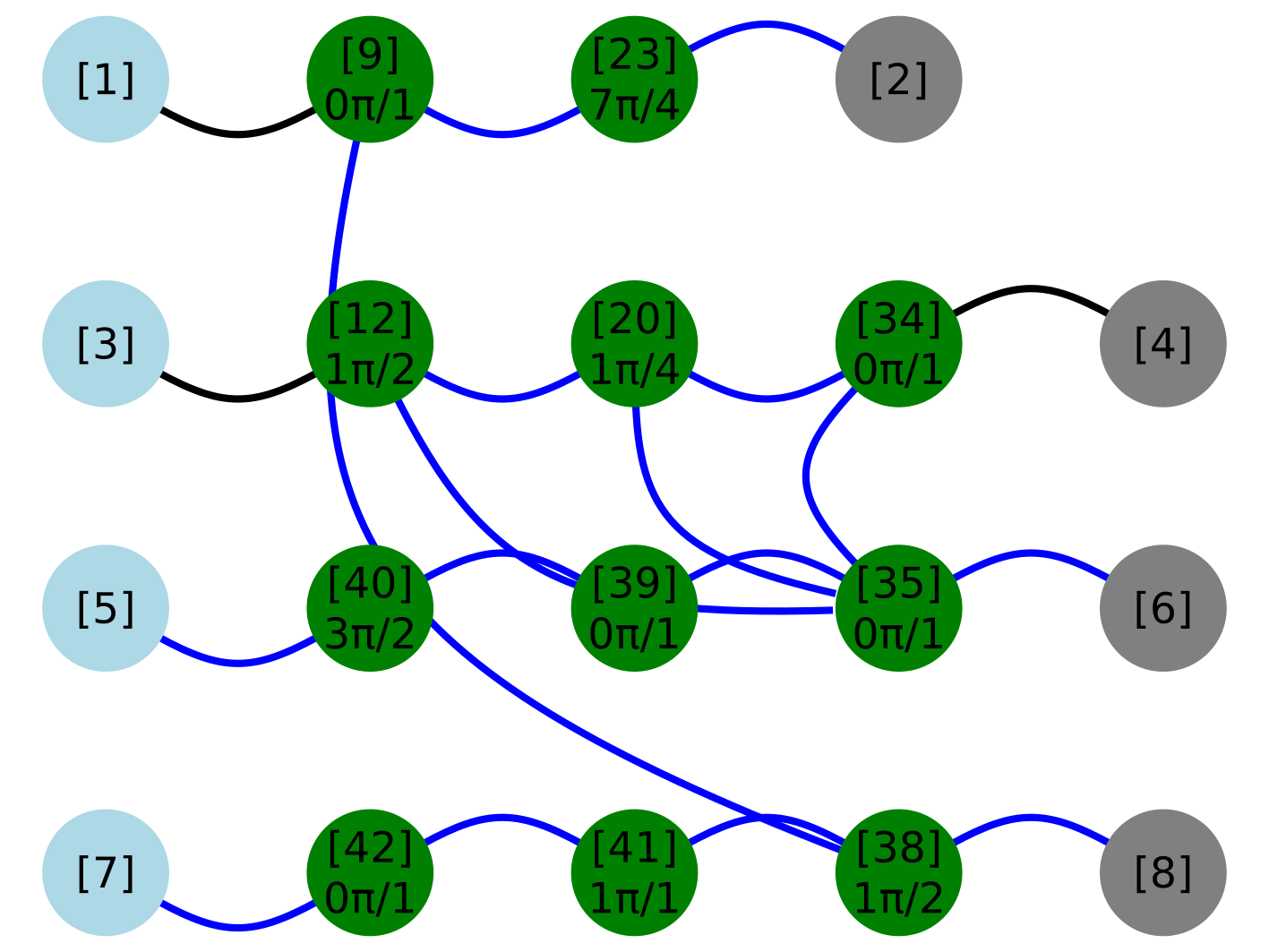

# extract circuit
cir = circuit_extraction(zxg)
ZXplot(cir)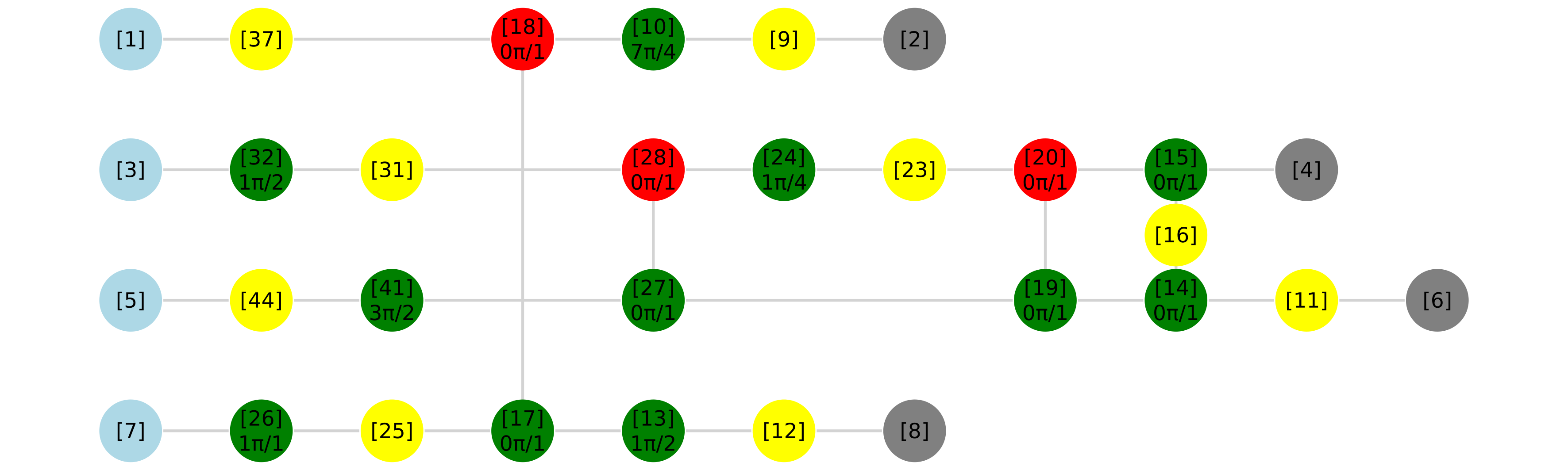

Наконец, мы получили упрощенную схему.

• [1]: "NON-IDENTITY-CHECK" IS QMA-COMPLETE
• [2]: Exact Non-identity check is NQP-complete
• [3]: Graph-theoretic Simplification of Quantum Circuits with the ZX-calculus
• [4]: Reducing T-count with the ZX-calculus

Метапрограммирование, квантовая компиляция и оптимизация схем при квантовой компиляции

В прошлом месяце я в основном работал над интеграцией с YaoLang.jl для ZXCalculus.jl. Это был мой первый опыт работы с метапрограммированием Джулии на практике. Я хочу поблагодарить своего наставника Роджера Ло за то, что он научил меня основным понятиям и полезным методам метапрограммирования.

Согласно Википедии, метапрограммирование — это метод программирования, при котором компьютерные программы имеют возможность обрабатывать другие программы как свои данные. чтобы понять метапрограммирование в Julia, необходимо знать, как работает компилятор Julia.

Как Julia работает

Все коды Джулии по сути строки (Strings), которые хранятся на диске. Когда мы запускаем коды Julia, Джулия сначала разбирает этот код на AST (абстрактные синтаксические деревья). AST будет храниться в виде выражений в структуре данных Expr в Julia. На этом уровне синтаксического анализа мы называем эти выражения IR (промежуточные представления) поверхностного уровня.

julia> s = "1 + 1 * 2"
"1 + 1 * 2"

julia> ex = Meta.parse(s)
:(1 + 1 * 2)

julia> dump(ex)
Expr
  head: Symbol call
  args: Array{Any}((3,))
    1: Symbol +
    2: Int64 1
    3: Expr
      head: Symbol call
      args: Array{Any}((3,))
        1: Symbol *
        2: Int64 1
        3: Int64 2

В этом примере ex — это AST. Его head — это :call, что означает, что это вызов функции. Он вызывает функцию + с аргументами 1 и еще одним Expr.

Затем опускаемся на уровень. На этом уровне макросы будут расширены, а "синтаксический сахар" Джулии будет преобразован в вызовы функций. Например, a[i] будет заменено на getindex(a, i). После серии преобразований, IR поверхностного уровня будет преобразован в SSA (Статическая форма единого назначения). IR также называется "пониженным" IR. В SSA IR каждая переменная может быть назначена только один раз. В Julia мы можем использовать макрос @code_lowed, чтобы увидеть SSA IR объекта Expr:

julia> @code_lowered 2 + 3
CodeInfo(
1 ─ %1 = Base.add_int(x, y)
└──      return %1
)

Джулия сделает вывод типа на SSA IR и оптимизирует его. А затем преобразует его в LLVM коды. Мы можем использовать макросы @code_typed и @code_llvm, чтобы увидеть эти IRs.

julia> @code_typed 2 + 3
CodeInfo(
1 ─ %1 = Base.add_int(x, y)::Int64
└──      return %1
) => Int64

julia> @code_llvm 2 + 3

;  @ int.jl:53 within '+'
; Function Attrs: uwtable
define i64 @"julia_+_15307"(i64, i64) #0 {
top:
  %2 = add i64 %1, %0
  ret i64 %2
}

Наконец, LLVM преобразует эти коды в собственные машинные коды.

julia> @code_native 2 + 3
        .text
; ┌ @ int.jl:53 within '+'
        pushq   %rbp
        movq    %rsp, %rbp
        leaq    (%rcx,%rdx), %rax
        popq    %rbp
        retq
        nopw    (%rax,%rax)
; └

Вот пикча из JuliaCon 2018, которая демонстрирует, как работает компилятор Julia.

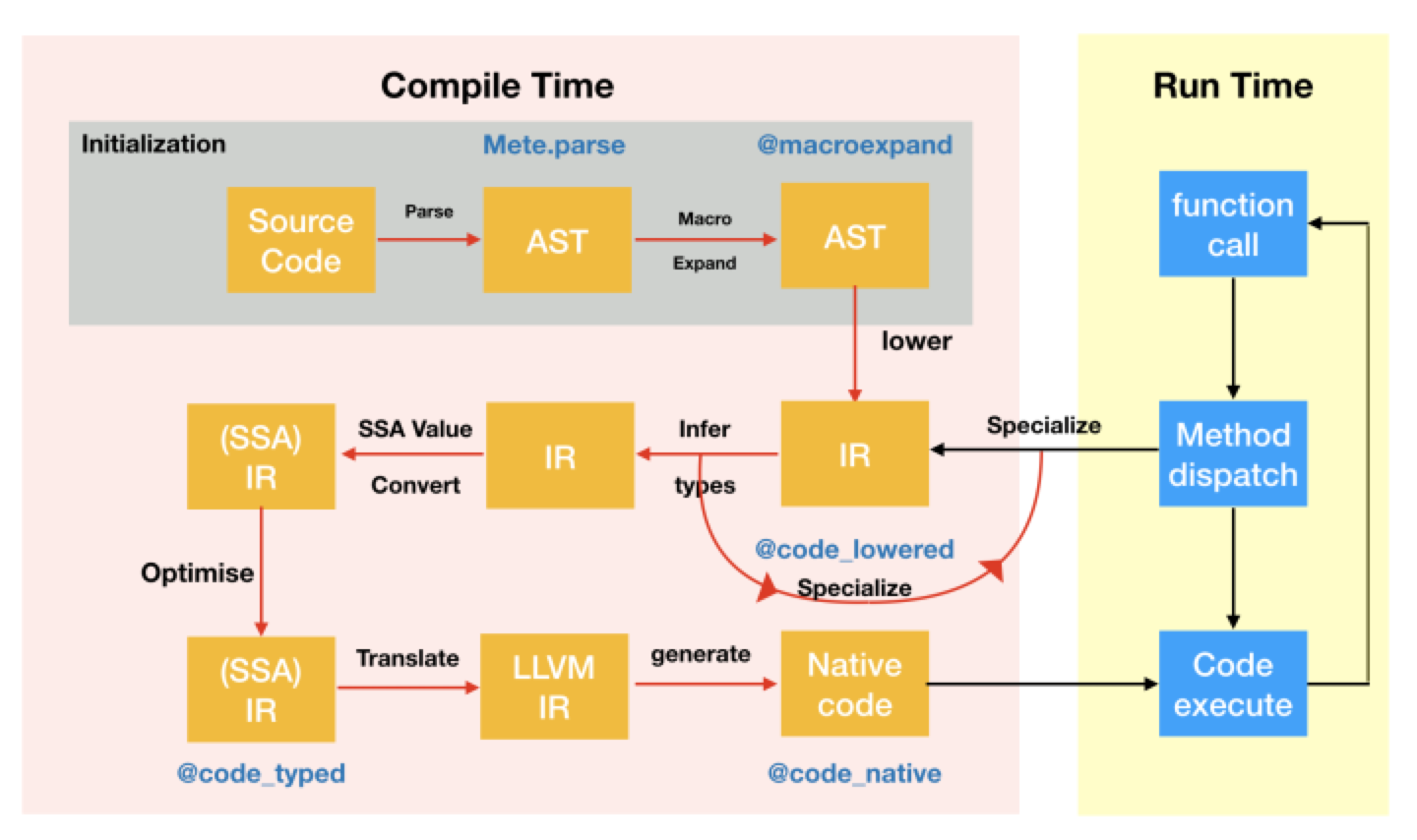
Как работает YaoLang.jl

Цель YaoLang.jl — построить удобный квантовый компилятор для гибридных квантово-классических программ в Julia. То есть, используя только несколько макросов и добавляя их к собственным функциям Julia, можно определить квантовые программы. В YaoLang.jl функция, украшенная макросом device, будет рассматриваться как функция с квантовыми операциями. В этих функциях макросы @ctrl, @measure, @expect и "синтаксический сахар" locs => gate доступны для определения квантовых операций. Например, представим схему для квантового преобразования Фурье n кубитов:

@device function qft(n::Int)
    1 => H
    for k in 2:n
        @ctrl k 1 => shift(2π / 2^k)
    end

    if n > 1
        2:n => qft(n - 1)
    end
end

Подобно процедурам компиляции Julia, макрос device будет анализировать функцию в IR поверхностного уровня в YaoLang.jl. Затем все макросы и синтаксический сахар для квантовых операторов будут заменены вызовами функций. Эти вызовы функций будут помечены меткой :quantum. Теперь IR поверхностного уровня будет преобразован в пониженный SSA IR. В YaoLang.jl SSA IR будет храниться в структуре данных YaoIR.

Остальные части — это оптимизация YaoIR и преобразование из него в коды аппаратного уровня. ZXCalculus.jl предназначен для оптимизации квантовых схем и должен быть интегрирован на уровне оптимизации.

Интеграция ZXCalculus.jl

Теперь мы рассматриваем только чисто квантовые программы. Как только мы получим YaoIR, чтобы оптимизировать квантовую схему, все, что нам нужно сделать, это следующие шаги

1. преобразовать его в ZX-диаграмму
2. Упростить ZX-диаграмму
3. Перевести упрощенную ZX-диаграмму обратно в YaoIR

Второй шаг уже реализован в ZXCalculus.jl. Нам нужно только реализовать преобразование между ZXDiagram и YaoIR.

YaoIR в ZXDiagram

Поскольку каждый YaoIR является SSA, мы можем просмотреть все утверждения, чтобы получить информацию о вентилях и их местоположениях. Для этого окинем взором самую обширную локацию по числу кубитов. Чтобы построить соответствующую ZX-диаграмму, построим пустую схему и последовательно протолкнем в нее гейты при обходе YaoIR. А код такой:

function ZXDiagram(ir::YaoIR)
    if ir.pure_quantum
        n = count_nqubits(ir)
        circ = ZXDiagram(n)
        stmts = ir.body.blocks[].stmts
        for stmt in stmts
            # push gates
        end
        return circ
    end
end

Поскольку параметризация ZX-диаграмм и квантовых схем может быть различной вплоть до глобальной фазы, то и ZX-диаграмма, которую мы получаем, может отличаться вплоть до глобальной фазы. Информация о глобальной фазе должна быть записана.

ZXDiagram в YaoIR

Мы предполагаем, что получаем ZXDiagram, представляющую квантовую схему. Чтобы преобразовать ее в YaoIR, нам нужно извлечь последовательность квантовых вентилей в ZXDiagram.

Их можно выудить из информации о расположении ZXDiagram. Так мы узнаем, как пауки сортируются от входа к выходу и высмотрим расположение кубитов для каждого паука. Если паук имеет степень 2, он представляет собой однокубитовый гейт. В противном случае он представляет собой вентиль с несколькими кубитами. Пройдя всех пауков от входа к выходу, мы можем получить последовательность квантовых вентилей. И тогда мы сможем построить новый YaoIR с этой последовательностью.

Параметры оптимизации

В "ZXCalculus.jl" существует несколько методов упрощения схем. И мы предлагаем реализовать другие методы упрощения, которые не основаны на ZX-исчислении. Необходимо предоставить пользователю возможность выбирать, какие методы оптимизации будут применяться.

Мы добавили эти параметры в макрос @device. Параметры оптимизации можно задать следующим образом

@device optimizer = [opt...] function my_circuit(args...)
    ...
end

Так optimizer вполне представим как подмножество [:zx_clifford, zx_teleport]. И мы добавим больше методов в будущем.

Примеры

К настоящему времени, ZXCalculus.jl была интегрирована с YaoLang.jl. Мы можем использовать YaoLang.jl для проверки правильности алгоритмов в ZXCalculus.jl. Данный пример представляет собой арифметическую схему.

Сначала мы определим два контура. Один — оригинальная схема, другой — оптимизированная.

using YaoLang

@device function test_cir()
    5 => H
    5 => shift(0.0)
    @ctrl 4 5 => X
    5 => shift($(7/4*π))
    @ctrl 1 5 => X
    5 => shift($(1/4*π))
    @ctrl 4 5 => X
    5 => shift($(7/4*π))
    @ctrl 1 5 => X
    4 => shift($(1/4*π))
    5 => shift($(1/4*π))
    @ctrl 1 4 => X
    4 => shift($(7/4*π))
    1 => shift($(1/4*π))
    @ctrl 1 4 => X
    @ctrl 4 5 => X
    5 => shift($(7/4*π))
    @ctrl 3 5 => X
    5 => shift($(1/4*π))
    @ctrl 4 5 => X
    5 => shift($(7/4*π))
    @ctrl 3 5 => X
    4 => shift($(1/4*π))
    5 => shift($(1/4*π))
    @ctrl 3 4 => X
    4 => shift($(7/4*π))
    5 => H
    3 => shift($(1/4*π))
    @ctrl 3 4 => X
    5 => shift(0.0)
    @ctrl 4 5 => X
    5 => H
    5 => shift(0.0)
    @ctrl 3 5 => X
    5 => shift($(7/4*π))
    @ctrl 2 5 => X
    5 => shift($(1/4*π))
    @ctrl 3 5 => X
    5 => shift($(7/4*π))
    @ctrl 2 5 => X
    3 => shift($(1/4*π))
    5 => shift($(1/4*π))
    @ctrl 2 3 => X
    3 => shift($(7/4*π))
    5 => H
    2 => shift($(1/4*π))
    @ctrl 2 3 => X
    5 => shift(0.0)
    @ctrl 3 5 => X
    5 => H
    5 => shift(0.0)
    @ctrl 2 5 => X
    5 => shift($(7/4*π))
    @ctrl 1 5 => X
    5 => shift($(1/4*π))
    @ctrl 2 5 => X
    5 => shift($(7/4*π))
    @ctrl 1 5 => X
    2 => shift($(1/4*π))
    5 => shift($(1/4*π))
    @ctrl 1 2 => X
    2 => shift($(7/4*π))
    5 => H
    1 => shift($(1/4*π))
    @ctrl 1 2 => X
    5 => shift(0.0)
    @ctrl 2 5 => X
    @ctrl 1 5 => X
end
cir = test_cir()

@device optimizer = [:zx_teleport] function teleport_cir()
    5 => H
    5 => shift(0.0)
    @ctrl 4 5 => X
    5 => shift($(7/4*π))
    @ctrl 1 5 => X
    5 => shift($(1/4*π))
    @ctrl 4 5 => X
    5 => shift($(7/4*π))
    @ctrl 1 5 => X
    4 => shift($(1/4*π))
    5 => shift($(1/4*π))
    @ctrl 1 4 => X
    4 => shift($(7/4*π))
    1 => shift($(1/4*π))
    @ctrl 1 4 => X
    @ctrl 4 5 => X
    5 => shift($(7/4*π))
    @ctrl 3 5 => X
    5 => shift($(1/4*π))
    @ctrl 4 5 => X
    5 => shift($(7/4*π))
    @ctrl 3 5 => X
    4 => shift($(1/4*π))
    5 => shift($(1/4*π))
    @ctrl 3 4 => X
    4 => shift($(7/4*π))
    5 => H
    3 => shift($(1/4*π))
    @ctrl 3 4 => X
    5 => shift(0.0)
    @ctrl 4 5 => X
    5 => H
    5 => shift(0.0)
    @ctrl 3 5 => X
    5 => shift($(7/4*π))
    @ctrl 2 5 => X
    5 => shift($(1/4*π))
    @ctrl 3 5 => X
    5 => shift($(7/4*π))
    @ctrl 2 5 => X
    3 => shift($(1/4*π))
    5 => shift($(1/4*π))
    @ctrl 2 3 => X
    3 => shift($(7/4*π))
    5 => H
    2 => shift($(1/4*π))
    @ctrl 2 3 => X
    5 => shift(0.0)
    @ctrl 3 5 => X
    5 => H
    5 => shift(0.0)
    @ctrl 2 5 => X
    5 => shift($(7/4*π))
    @ctrl 1 5 => X
    5 => shift($(1/4*π))
    @ctrl 2 5 => X
    5 => shift($(7/4*π))
    @ctrl 1 5 => X
    2 => shift($(1/4*π))
    5 => shift($(1/4*π))
    @ctrl 1 2 => X
    2 => shift($(7/4*π))
    5 => H
    1 => shift($(1/4*π))
    @ctrl 1 2 => X
    5 => shift(0.0)
    @ctrl 2 5 => X
    @ctrl 1 5 => X
end
tp_cir = teleport_cir()

С помощью пакета YaoArrayRegister.jl, мы можем вычислить матрицу для каждой схемы.

using YaoArrayRegister

mat = zeros(ComplexF64, 32, 32)
for i = 1:32
    st = zeros(ComplexF64, 32)
    st[i] = 1
    r0 = ArrayReg(st)
    r0 |> cir
    mat[:,i] = r0.state
end

tp_mat = zeros(ComplexF64, 32, 32)
for i = 1:32
    st = zeros(ComplexF64, 32)
    st[i] = 1
    r1 = ArrayReg(st)
    r1 |> tp_cir
    tp_mat[:,i] = r1.state
end

Сравнивая эти две матрицы, мы видим, что они идентичны. Следовательно, алгоритм возвращает эквивалентную упрощенную схему.

sum(abs.(mat - tp_mat) .> 1e-14) == 0

Итого

Во время второго этапа кодирования я реализовал преобразование между "ZXDiagram" и "YaoIR", что обеспечивает интеграцию ZXCalculus".jl с YaoLang.jl. Кроме того, документация теперь доступна здесь. И во время испытания ZXCalculus".jl с помощью YaoLang.jl и YaoArrayRegister.jl я нашел несколько ошибок в реализации извлечения контуров и фазовой телепортации. Эти ошибки уже исправлены.

На следующем этапе я буду работать над компиляцией кодов OpenQASM в коды YaoIR. Это позволит нам читать схемы из кода OpenQASM. А также протестирую результативность ZXCalculus.jl на некоторых эталонных схемах и сравню его с PyZX.

Упрощение квантовой схемы

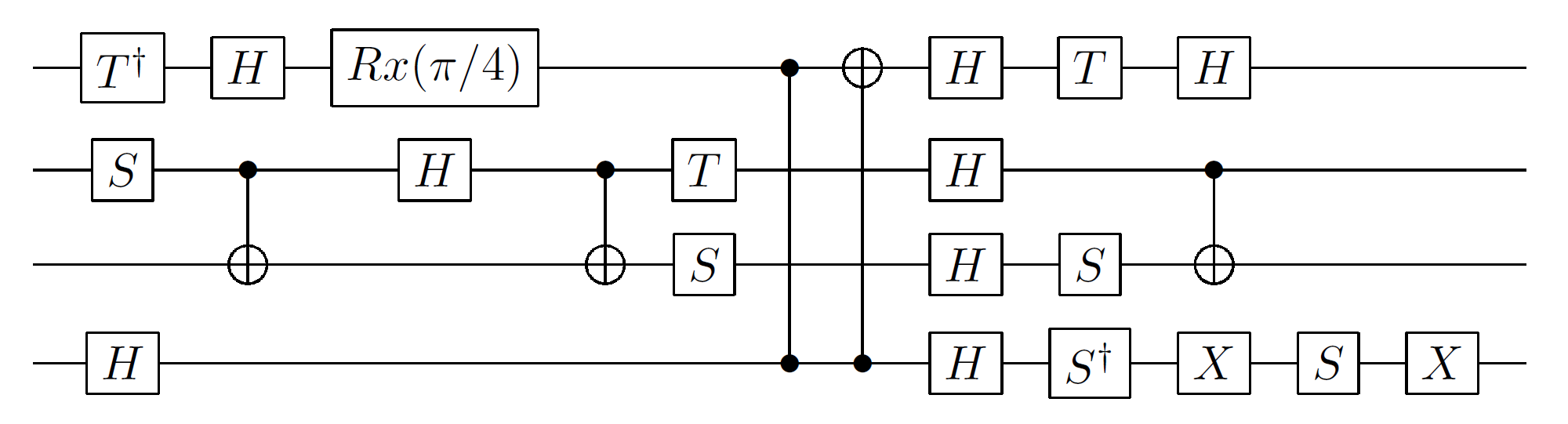
Предположим, что у нас есть квантовая схема с 24 гейтами, как описано выше. Мы можем определить эту схему с помощью YaoLang.jl используя макрос @device. YaoLang.jl — это компилятор для гибридных квантово-классических программ, которые очень практичны в нынешнюю эпоху NISQ (noisy intermediate-scale quantum). Кроме того, YaoLang.jl интегрирован с ZXCalculus.jl.

julia> using YaoLang;

julia> @device optimizer = [:zx_teleport] function demo_circ_simp()
           1 => shift($(7π/4))
           1 => H
           1 => Rx($(π/4))
           4 => H
           @ctrl 1 4 => Z
           @ctrl 4 1 => X
           1 => H
           4 => H
           1 => T
           4 => shift($(3π/2))
           4 => X
           1 => H
           4 => S
           4 => X
           2 => S
           @ctrl 2 3 => X
           2 => H
           @ctrl 2 3 => X
           2 => T
           3 => S
           2 => H
           3 => H
           3 => S
           @ctrl 2 3 => X
       end
demo_circ_simp (generic circuit with 1 methods)

Можно добавить аргумент optimizer = [opts...] в макрос @device, чтобы упростить эту схему во время компиляции. В настоящее время существует только два этапа оптимизации: :zx_clifford для упрощения Клиффорда [1] и :zx_teleport для фазовой телепортации [2]. Например, с помощью optimizer = [:zx_teleport] компилятор вызовет алгоритм фазовой телепортации в ZXCalculus.jl для упрощения схемы.

Мы можем использовать макрос @code_yao, чтобы увидеть, какая схема у нас есть. В этом примере количество гейтов схемы было уменьшено с 24 до 20.

julia> using YaoLang.Compiler

julia> gate_count(demo_circ_simp)
Dict{Any,Any} with 8 entries:
  "YaoLang.Rx(3.141592653589793)"     => 2
  "YaoLang.H"                         => 6
  "YaoLang.Rx(0.7853981633974483)"    => 1
  "YaoLang.shift(4.71238898038469)"   => 1
  "YaoLang.shift(1.5707963267948966)" => 4
  "YaoLang.shift(0.7853981633974483)" => 1
  "@ctrl YaoLang.Z"                   => 1
  "@ctrl YaoLang.X"                   => 4

Мы можем использовать YaoArrayRegister.jl чтобы применить эту упрощенную схему к квантовому состоянию:

julia> using YaoArrayRegister;

julia> circ_teleport = demo_circ_simp()
demo_circ_simp (quantum circuit)

julia> r = rand_state(4);

julia> r |> circ_teleport
ArrayReg{1, Complex{Float64}, Array...}
    active qubits: 4/4

Можно также загрузить схемы из OpenQASM. OpenQASM — это квантовая инструкция. Коды OpenQASM можно запускать на квантовых устройствах IBM. А квантовые схемы могут храниться в виде кодов OpenQASM. Я использовал пакет Джулии RBNF.jl (парсит код в ограниченную форму Бэкуса-Наура) для перевода OpenQASM кодов в AST, с последующим преобразованием его в YaoIR, промежуточное представление для смешанной квантово-классической программы YaoLang.jl. Это делает возможным чтение схем из OpenQASM в ZXCalculus.jl через YaoLang.jl.

using YaoLang: YaoIR, is_pure_quantum
using ZXCalculus

lines = readlines("gf2^8_mult.qasm")
src = prod([lines[1]; lines[3:end]])
ir = YaoIR(@__MODULE__, src, :qasm_circ)
ir.pure_quantum = is_pure_quantum(ir)

circ = ZXDiagram(ir)
pt_circ = phase_teleportation(circ)

Здесь мы загрузили схему в виде ZXDiagram из файла .qasm, который можно найти тут. И мы использовали алгоритм фазовой телепортации, чтобы упростить его. Мы видим, что Т-число в цепи уменьшилось с 448 до 264.

julia> tcount(circ)
448

julia> tcount(pt_circ)
264

Приведенные выше примеры показали, как ZXCalculus.jl работает в качестве механизма упрощения схем в YaoLang.jl. А теперь давайте посмотрим, что скрывается за сценой.

Низкоуровневые интерфейсы ZXCalculus

В ZX-исчислении мы будем иметь дело с ZX-диаграммами и мультиграфами с некоторой дополнительной информацией. Каждая вершина ZX-диаграммы называется пауком. Есть два типа пауков, Z-паук и X-паук. Каждый паук связан с числом, называемым фазой. По нотации Дирака Z-паук и X-паук представляют собой следующие матрицы ранга 2.

ZX-диаграммы можно рассматривать как особый тип тензорной сети. Как и квантовые схемы. А квантовые схемы могут быть преобразованы в ZX-диаграммы по следующим правилам.

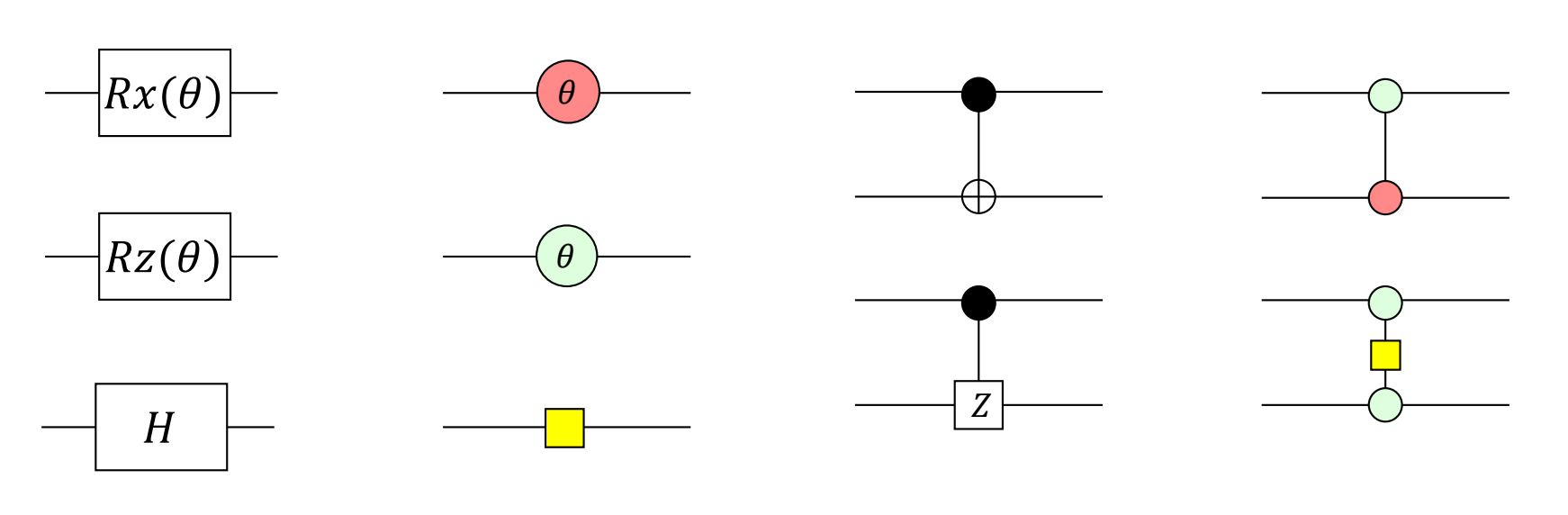
Желтая коробка, H-box, — это простая нотация следующих пауков в ZX-исчислении

Для представления общих ZX-диаграмм мы определили структуру ZXDiagram в ZXCalculus.jl. Мы можем построить ZX-диаграмму, которая представляет собой пустую квантовую схему с n кубитами с помощью ZXDiagram(n). Например, если мы хотим упростить приведенную выше схему с помощью ZXCalculus.jl вручную, то сначала мы построим ZX-диаграмму схемы из 4 кубитов.

using ZXCalculus
zxd = ZXDiagram(4)

Затем мы добавляем некоторые элементы к ZX-диаграмме, которую мы только что построили. Просто используем push_gate! и push_ctrl_gate!

push_gate!(zxd, Val(:Z), 1, 7//4)
push_gate!(zxd, Val(:H), 1)
push_gate!(zxd, Val(:X), 1, 1//4)
push_gate!(zxd, Val(:H), 4)
push_ctrl_gate!(zxd, Val(:CZ), 4, 1)
push_ctrl_gate!(zxd, Val(:CNOT), 1, 4)
push_gate!(zxd, Val(:H), 1)
push_gate!(zxd, Val(:H), 4)
push_gate!(zxd, Val(:Z), 1, 1//4)
push_gate!(zxd, Val(:Z), 4, 3//2)
push_gate!(zxd, Val(:X), 4, 1//1)
push_gate!(zxd, Val(:H), 1)
push_gate!(zxd, Val(:Z), 4, 1//2)
push_gate!(zxd, Val(:X), 4, 1//1)
push_gate!(zxd, Val(:Z), 2, 1//2)
push_ctrl_gate!(zxd, Val(:CNOT), 3, 2)
push_gate!(zxd, Val(:H), 2)
push_ctrl_gate!(zxd, Val(:CNOT), 3, 2)
push_gate!(zxd, Val(:Z), 2, 1//4)
push_gate!(zxd, Val(:Z), 3, 1//2)
push_gate!(zxd, Val(:H), 2)
push_gate!(zxd, Val(:H), 3)
push_gate!(zxd, Val(:Z), 3, 1//2)
push_ctrl_gate!(zxd, Val(:CNOT), 3, 2)

Теперь давайте нарисуем ZX-диаграмму, которую мы построили. Инструмент визуализации ZXCalculus.jl в настоящее время предоставляется в YaoPlots.jl.

using YaoPlots
plot(zxd)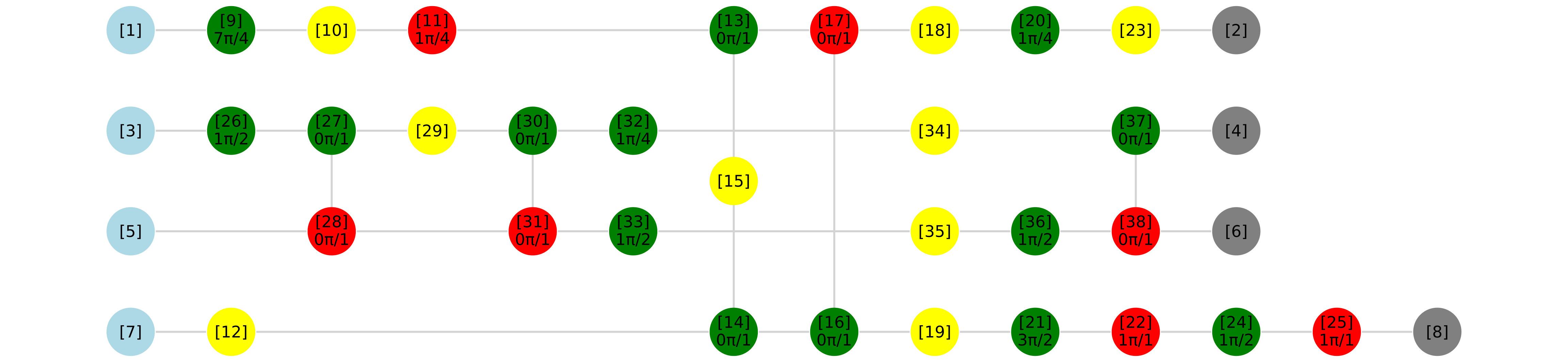

Заодно поднимем алгоритмы упрощения clifford_simplification [1] и phase_teleportation [2]

ex_zxd = clifford_simplification(zxd);
pt_zxd = phase_teleportation(zxd);
plot(ex_zxd)
plot(pt_zxd)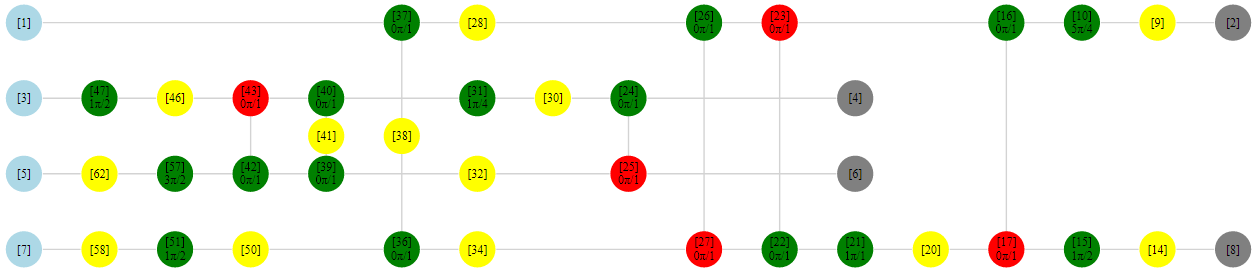

Схема после упрощения Клиффорда

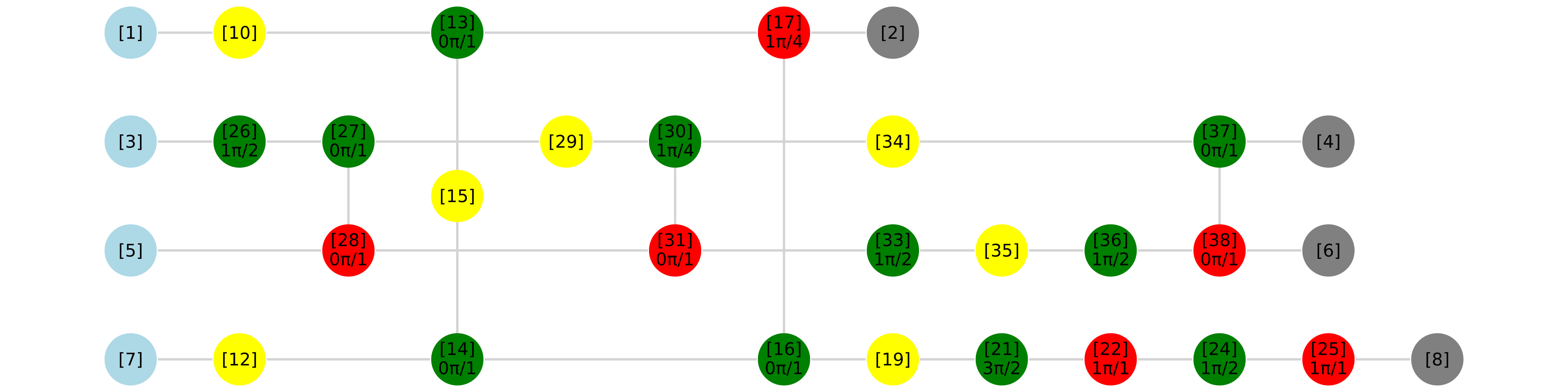
Схема после фазовой телепортации

Алгоритм фазовой телепортации может уменьшить число Т-вентилей квантовой схемы. Воспользуемся tcount чтобы показать количество Т-вентилей. В этом примере число Т уменьшилось с 4 до 2.

julia> tcount(zxd)
4

julia> tcount(pt_zxd)
2

Эти алгоритмы используют правила ZX-исчисления для упрощения ZX-диаграмм. Эти правила определяют, как ZX-диаграммы могут быть преобразованы. Вот некоторые основные правила для ZXDiagram.

В работе [1] определен особый тип ZX-диаграммы — графоподобная ZX-диаграмма. Мы используем ZXGraph, чтобы представить ее в ZXCalculus.jl. И вот некоторые правила для ZXGraph

Можно применить правила на ZX-диаграмме вручную. Для этого мы предоставляем различные API.

Функция match найдет все вершины соответствующие заданному правилу. Применение rewrite! переписывает ZX-диаграмму на некоторых совпадающих вершинах. replace! функция просто сопоставляет и переписывает все совпадающие вершины один раз. simplify! функция будет сопоставлять и переписывать ZX-диаграмму с правилом до тех пор, пока не останется сопоставимых вершин.

В clifford_simplification, мы сначала преобразуем заданную ZX-диаграмму в графоподобную ZX-диаграмму

zxg = ZXGraph(zxd)
plot(zxg)

Затем, мы упрощаем ее с помощью правил :lc, :p1, и :pab

simplify!(Rule{:lc}(), zxg)
simplify!(Rule{:p1}(), zxg)
replace!(Rule{:pab}(), zxg)
plot(zxg)

Наконец, мы извлекаем новую схему из упрощенной графоподобной ZX-диаграммы

ex_circ = circuit_extraction(zxg)
plot(ex_circ)

Почему именно ZXCalculus.jl?

Вышеприведенные алгоритмы уже реализованы в пакете Python PyZX. PyZX — это полнофункциональная библиотека для манипулирования крупномасштабными квантовыми схемами и ZX-диаграммами. Он предоставляет множество удивительных возможностей визуализации и поддерживает различные формы квантовых схем, включая QASM, Quipper и Quantomatic.

Так почему же мы разработали ZXCalculus.jl? Это связано с тем, что ZXCalculus.jl является не только полнофункциональной библиотекой для ZX-исчисления, но и одним из механизмов упрощения схем для YaoLang.jl. Легкая нативная реализация ZX-исчисления необходима, так как зависимость от пакета Python сделает работу компилятора медленнее и сложнее.

Benchmarks

Мы провели сравнительный анализ алгоритма фазовой телепортации на 40 схемах с различным числом вентилей (от 57 до 91642). ZXCalculus.jl имеет ускорение от 6 до 50 раз в этих примерах (время выполнения ZXCalculus.jl масштабируется до 1 для каждой схемы на этом рисунке). Эти тесты выполняются на ноутбуке с процессором Intel i7-10710U и 16 ГБ оперативной памяти. Код для бенчмарков можно найти здесь.

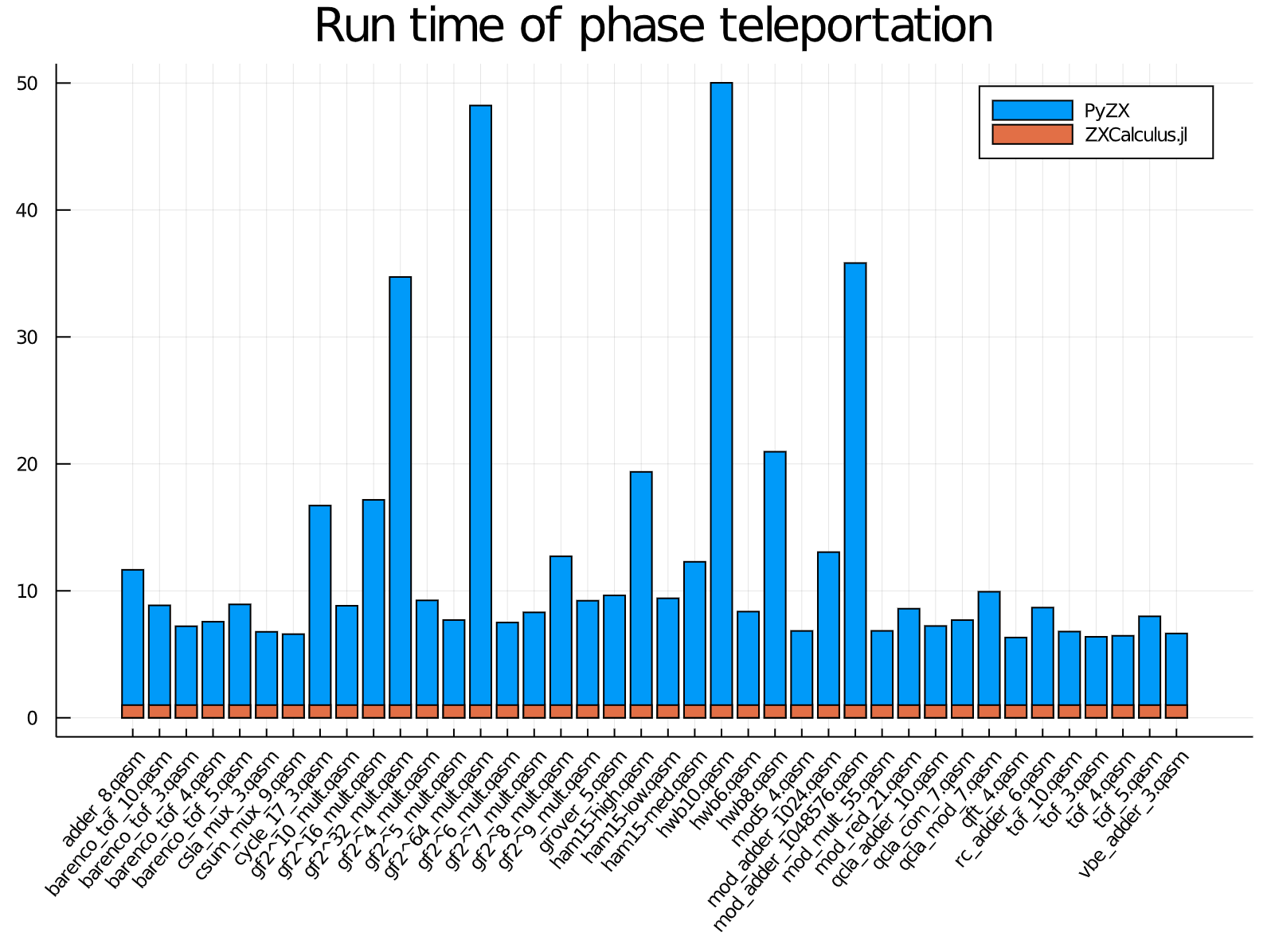
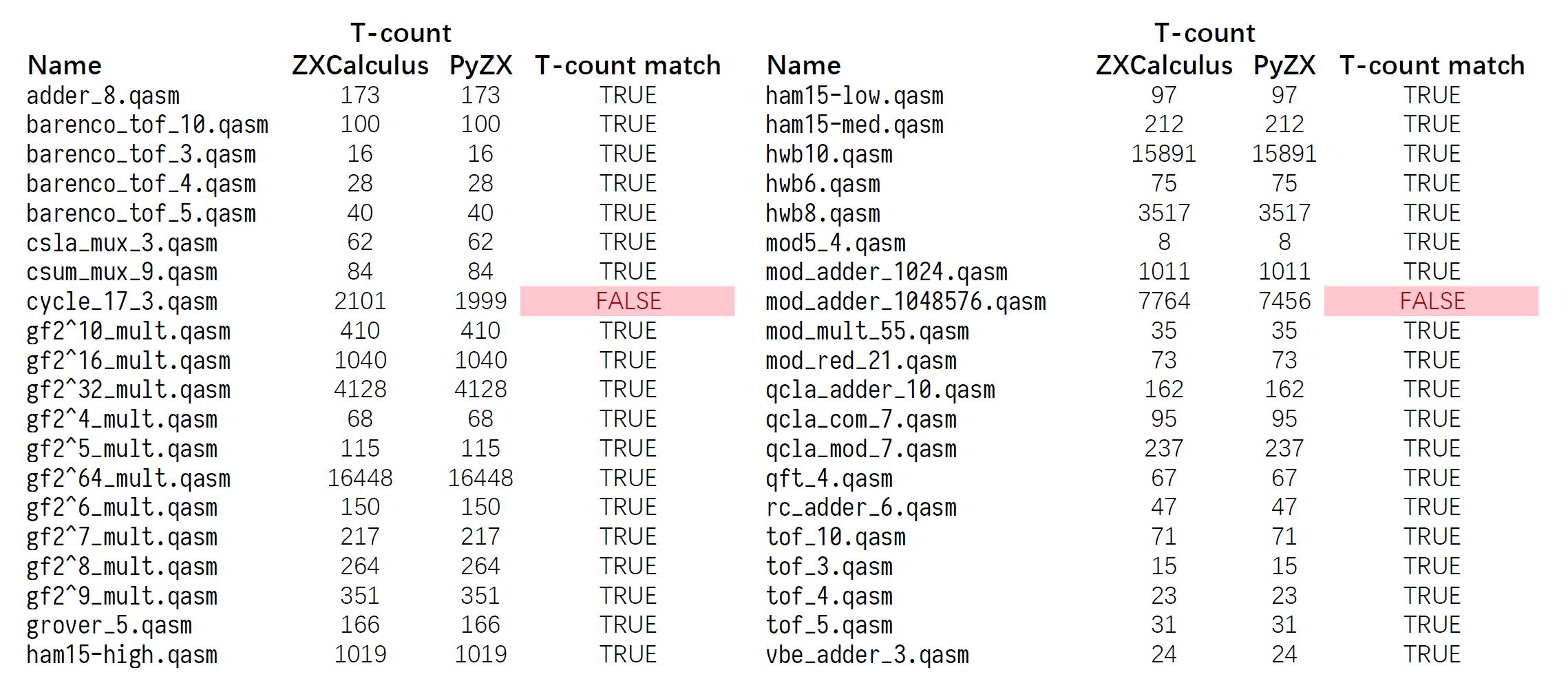
В большинстве примеров T-число оптимизированных схем, производимых ZXCalculus.jl, совпадает с PyZX. Однако в 2 примерах ZXCalculus.jl имеет больше T-count, чем PyZX. Это может быть вызвано различными стратегиями упрощения между ZXCalculus.jl и PyZX. Мы продолжим исследовать это в будущем.

Кроме того, YaoLang.jl поддерживает гибридные квантово-классические программы. Можно оптимизировать гибридные квантово-классические программы с помощью ZXCalculus.jl.

Резюме и дальнейшей работы

В течение GSoC 2020 я в основном выполнил следующие работы.

• Представление и манипулирование ZX-диаграммами с высокой производительностью.
• Реализация двух алгоритмов упрощения на основе ZX-исчисления.
• Добавление визуализации в ZX-схемы в YaoPlots.jl.
• Интеграция ZXCalculus.jl с YaoLang.jl.
• Добавление поддержки OpenQASM в YaoLang.jl.

Есть еще кое-что, что нужно отполировать.

• Поиск лучшей стратегии упрощения, чтобы получить более низкие значения T.
• Полная поддержка визуализации "ZXGraph" (сценарий построения графика может потерпеть неудачу на некоторых "ZXGraph" с фазовыми гаджетами).
• Преобразование на ZX-схемы для тензорных сетей без YaoLang.jl.
• Преобразование между "YaoIR" и "ZXDiagram" может привести к тому, что схема отличается от глобальной фазы. Мы должны записать эту глобальную фазу в более поздней версии.

Кроме того, я буду продолжать работать над YaoLang.jl с Роджером Ло, Чтобы поддерживать больше методов упрощения схем (методы сопоставления шаблонов, методы на основе Quon и т.д.).

Благодарности

Я хочу поблагодарить своих наставников, Роджера Ло и Цзиньго Лю. Без их помощи я не смог бы осуществить этот проект. ZXCalculus.jl очень вдохновлен PyZX. Спасибо Алекс Киссинджер и Джон ван де Ветеринг, авторам PyZX. Они дали мне полезные советы по алгоритму фазовой телепортации и рассмотрели бенчмарки между PyZX и ZXCalculus.jl. Благодарю Google за проведение Google Summer of Code, которое способствует развитию сообщества с открытым исходным кодом.

[1]: Graph-theoretic Simplification of Quantum Circuits with the ZX-calculus
[2]: Reducing T-count with the ZX-calculus