
Статья может быть интересна и полезна студентам, инженерам и разработчикам, работающим над созданием цифровых систем радиосвязи. Рассчитана на пользователей, владеющих минимальными основами работы в среде разработки Octave (MatLab). Однако, для понимания могут потребоваться довольно глубокие знания радиотехники и математики.
Имитационная модель будет настолько проста, что в ней даже не будет частоты дискретизации, не будет несущей частоты, не будет скорости передачи данных, не будет мощности передаваемого сигнала. Тем не менее, всё это будет учтено, ведь мы хотим создать универсальную модель, справедливую для любых комбинаций этих параметров. Как же так, — скажут инженеры, — как можно создавать такие модели, в которых нет самых необходимых параметров? Ведь модуляция — это изменение одного из параметров несущей, то есть её амплитуды, частоты или фазы. Вот и попробуем разобраться, что к чему, а заодно прикоснёмся к тому, что называют наукой.
Цель, которую будем преследовать созданием этой модели, сформулируем таким образом: выяснить зависимость вероятности битовой ошибки (BER) для разных отношений сигнал/шум при передаче двоичных данных с помощью сигналов с фазовой манипуляцией в канале с аддитивным белым гауссовским шумом (АБГШ) в качестве помехи, при этом текст программы должен быть коротким. Хочется сразу предупредить, что краткость не означает понятность и наглядность, скорее это означает бОльшую насыщенность информацией, то есть, придётся писать мало текста программы, но много букв. Тем интереснее должно быть специалистам, статья писалась для того, чтобы показать имитационное моделирование процесса передачи сигналов немного в необычном ракурсе.
Тот, кто хоть раз запускал Octave, уже знает, что текст программы представляет собой скрипт, выполняемый построчно. Модель и будет представлять собой скрипт, который выполняется в среде Octave, и может быть легко перенесён в MatLab. Сам скрипт представляет собой обычный текстовый файл, как и в любом другом языке программирования.
Имитационная модель — это что-то похожее на реальный объект, но имеющее некоторые упрощения. Классическое определение канала связи включает в себя источник информации, среду распространения и получатель информации. Именно в таком порядке и будем создавать модель.
Итак, в соответствии с ТЗ:
Берём данные (нули, единицы)
Модулируем фазу несущей данными
Накладываем шумы с заданным соотношением мощностей сигнала и шума
Демодулируем полученную смесь
Сравниваем принятые данные с переданными
Считаем ошибки
Строим график вероятности появления ошибок (хорошо было бы оценить адекватность модели, чтобы понять достигнута ли цель)
- Уууу, как много! - скажет кто-то.
Погодите, модель будет короче, чем этот список.
Прежде чем перейдём к подробностям, как всегда немного магии и приготовлений. Любую модель советую начать с волшебной строки скрипта:
clear; clc; close all;Это позволяет во-первых, очистить переменные в рабочей области (clear), то есть обнулить исходные данные, во-вторых, очистить командное окно (clc), куда обычно выводятся ошибки и результаты каких-то промежуточных вычислений, и в-третьих, закрыть все открытые графики (close all), которых бывает получено несколько и чтобы каждый из них не закрывать по одному, можно сделать это одним махом при запуске скрипта на выполнение. А вообще эта строка позволит избежать многих неприятностей в будущем. Когда вы что-то будете делать с переменными в рабочей области, то есть менять их значения, тогда запуск скрипта без их обнуления может привести к неожиданным результатам, или вообще к ошибкам, то есть запуск скрипта на выполнение с этой волшебной строкой в самом начале будет как с чистого листа.
С магией закончили, далее приготовления. Постольку, поскольку нам надо получить зависимость от отношения сигнал/шум, так почему бы его сразу же и не задать. Только надо помнить о том, что в цифровых системах связи мы будем задавать не само отношение сигнал шум, оно малоинформативно, а задавать будем отношение энергии бита к спектральной плотности мощности шума, которое обычно так и обозначается Eb/N0. И сделаем это так:
EbN0 = -5:5;Так мы задали сразу ряд необходимых соотношений, то есть вектор, содержащий числа от минус 5 дБ до плюс 5 дБ с шагом 1 дБ (шаг тоже указывается через двоеточие, но по умолчанию он и так равен 1 и нас это устраивает).
Результаты вычислений будем складывать в переменную, размер которой должен совпадать с размером EbN0, то есть создадим переменную, содержащую битовые ошибки (BER) таким образом:
BER=zeros(1,length(EbN0));То есть запишем туда столько нулей с помощью функции zeros(), сколько самих точек построения будущего графика, функция length() как раз позволяет узнать длину вектора EbN0, теперь переменная BER это вектор-строка как и переменная EbN0.
Для того, чтобы правильно задать соотношение мощностей сигнала и помехи потребуется множитель, на который мы умножим амплитуду сигнала, чтобы получить желаемое соотношение EbN0. Для этого достаточно вспомнить, что это отношение в дециБеллах есть:
где As — амплитуда сигнала, а An — мощность шума. И этот логарифм уже задан у нас в виде ряда значений, от этого ряда надо перейти обратно к множителю «в разах», то есть выразить из этой формулы само отношение амплитуд, в Octave это будет выглядеть так:
mnozh = 10.^(EbN0/20);Об операторе «точка» после цифры 10 не забываем, ведь EbN0 это вектор, и чтобы получить поэлементную операцию возведения в степень, а не матричную, точка необходима. На это число мы будем умножать наш передаваемый сигнал перед тем как наложить на него шум, в итоге смесь будет иметь заданное отношение EbN0.
Разумеется передать бит один раз с заданным EbN0 недостаточно для получения величины ошибки, для этого надо набрать определённую статистику. С одной стороны, чем больше будет количество переданных бит, тем точнее получится вычислить вероятность ошибки. Но необходимо помнить, что если это число будет слишком большим, вычисления могут производиться очень долго. Но и это ещё не всё. Здесь надо сказать, что при малых отношениях EbN0 ошибок довольно много, и нет необходимости брать слишком большое количество передаваемых бит, а вот при больших отношения EbN0 ошибки будут редкими и для обеспечения необходимой точности лучше взять число битов (NN) побольше, поэтому предлагаю поступить следующим образом:
NN = 1000*(EbN0-EbN0(1)+1);Ряд чисел EbN0 должен быть возрастающим, и по этой хитрой формуле, взятой из справочника Потолоцкого, получается, что при поэлементном вычитании из каждого числа ряда значений EbN0 первого элемента EbN0(1) получим возрастающий ряд чисел от нуля до некоторого положительного числа. Отношение EbN0 начинает изменяться от минус 5 дБ, и так как число передаваемых бит не может быть отрицательным или нулевым, то начальное количество опытов будет 1000, далее NN будет равно 2000, когда EbN0 = -4 и так далее, и когда EbN0 будет равно 5, NN достигнет 11000. Сделано это с тем, чтобы при моделировании задавать только отношение EbN0. Если понадобится передать больше или меньше бит данных можно число 1000 поменять или сделать переменной.
С приготовлениями закончили, дальше будет самое интересное, потому что пункты ТЗ пойдут прямо по порядку и подробнее:
1. Берём данные, то есть начнём с источника информации. Ни для кого не секрет, что в настоящее время передача осуществляется двоичными данными, то есть на каждом элементарном интервале времени времени передаётся один из двух бит «0» или «1». Для простоты передавать всегда будем один и тот же бит данных, например «1», и передавать его будем столько раз сколько захотим.
2. Модулируем фазу несущей взятыми данными. Кратко о модуляции — BPSK (binary phase shift keying) переводится на русский язык как двоичная фазовая манипуляция. Выбрана BPSK потому, что она так и манит своей максимальной помехоустойчивостью. То есть информация закладывается в угол начального поворота фазы несущего колебания в передатчике, а в приёмнике наоборот извлекается из текущего положения фазы несущей. Вот тут-то нам и понадобятся математика, Пифагор и комплексные числа. Как хорошо, что можно написать слово «комплексный» без ударения, каждый читатель сам определится, куда его поставить на «о» или на «е».
Сейчас практически все цифровые способы модуляции основаны на применении универсального квадратурного модулятора, для которого нужна комплексная огибающая, или проще говоря две квадратуры — действительная и мнимая. Чтобы наш информационный бит «1» просто взять и поместить на несущую вспомним сигнальное созвездие.
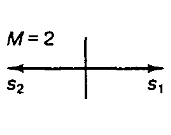
Куда бы ни попал вращающийся с любой частотой вектор несущей в произвольный момент времени передачи, для передачи единицы мы должны взять начальную фазу равную 0 градусов. На сигнальном созвездии это соответствует точке с координатами 1+0*i, то есть действительная квадратура равна единице, а мнимая равна нулю. Так как амплитуда неизменна и будет равна единице, а частота может быть любой, то комплексное число 1+0*i задаёт начальную фазу 0 градусов и этого нам для модели модулятора достаточно. Другими словами, наш модулятор каждый раз будет формировать комплексное число 1+0*i при необходимости передать «1», потому что напомню передавать необходимо один и тот же бит. Итак, сигнал на выходе BPSK модулятора, передающий один информационный бит в Octave, будет выглядеть так:
sig = 1+1i*0;Это одно комплексное число, цифра. И эту операцию мы даже в основной цикл помещать не будем для экономии быстродействия. Всё, с источником информации и модуляцией закончили. Таким образом, мы передадим данные и промодулируем несущую без использования частоты дискретизации и без использования численного значения несущей, и даже без использования скорости передачи, потому что она тоже может быть любой. Но это НЕ означает, что полученные результаты не будут справедливыми, наоборот, это означает, что полученные результаты будут одинаково справедливы для любой скорости передачи данных с любой частотой дискретизации и на любой несущей частоте. Было бы странно, если бы передача была возможна только на какой-то одной скорости или частоте, которая заложена в модели.
Далее расположен основной цикл программы, в который будет вложен ещё один цикл. Во внешнем цикле мы будем перебирать задаваемые отношения EbN0 через номер n, а во внутреннем цикле будем повторять передачу заданное количество NN раз, и так как оно переменное, то будем перебирать NN, изменяя номер k. Если бы количество бит NN было постоянное, можно было сократить модель ещё на одну строку, но для наукообразности и для объёма статьи всё же оставим строку вложенного цикла (это была шутка):
for n = 1:length(EbN0)
for k = 1:NN(n)Внутри циклов будут расположены следующих четыре шага моделирования (с номерами 3, 4, 5 и 6).
3. Накладываем шумы с заданным соотношением мощностей сигнала и шума. Для этого генерируем шум:
shum = (randn(1,1)+1i*randn(1,1))/sqrt(2);Здесь опять требуются пояснения. Аддитивный белый гауссовский шум можно сымитировать наложением нормальных случайных величин. Таким образом, при передаче каждого бита случайная величина будет генерироваться заново - функция randn(1,1) возвращает одно случайное число, распределённое по нормальному закону. И, так как сигнал комплексный, то и шум должен быть комплексным, состоящим из действительного и мнимого числа. А чтобы его средняя амплитуда строго соответствовала амплитуде сигнала и была равна единице, сумму квадратур придётся разделить на корень из двух по теореме Пифагора.
Перед демодуляцией надо сформировать аддитивную смесь. У нас имеется множитель амплитуды с номером n, мы его умножим на сигнал и добавим шум, например так: mnozh(n)*sig+shum. Но это ещё не всё, поэтому сразу же и:
4. Демодулируем полученную смесь. Демодуляция это сложно, это будет две строки, а синхронизация — это очень сложно, поэтому вообще пока не будем её показывать, будем считать синхронизацию идеальной. Для демодуляции фазоманипулированного сигнала в простейшем случае используют фазовый детектор и фильтр. Всё это можно сделать одним махом через преобразование Фурье - функция fft(), там есть уже и квадратурное гетеродинирование и вычисление фаз и амплитуд, и фильтрация, не зря же его придумал этот замечательный учёный аж два века назад. К тому же у нас имеется всего лишь один единственный отсчёт смеси сигнала с шумом, поэтому скорость вычислений будет как двойка в нулевой степени, то есть быстродействие будет коньком нашей модели. То есть мы можем демодулировать сигнал вычислив спектральный состав (spec) нашей смеси сигнала с шумом, и всё это в одной строке:
spec = fft(mnozh(n)*sig+shum);А теперь небольшой секрет, преобразование Фурье от одного отсчёта равно самому отсчёту, поэтому будет работать даже без функции fft(), то есть так: «spec = mnozh(n)*sig+shum;». Однако на будущее оставим предыдущий вариант, как более корректный в общем случае, вдруг кому-то понравится и читатели заинтересуются продолжением, потому что добавив 5 строчек к этой модели её можно сделать уже не такой короткой, но гораздо более наглядной и можно увидеть кусочки синусоид, а пока этого сделать нельзя. Синусоиды ближе к сердцу любого радиоинженера, потому что чуть ближе к практике, но чуть-чуть дальше от науки.
Это была первая строка имитационной модели демодулятора, второй строкой мы выделим переданную информацию, то есть начальную фазу, тот начальный угол поворота, который содержит передаваемую информацию, для этого есть функция angle():
phaza = angle(spec);Осталось сравнить полученный угол с переданным, напомню, передавали логическую единицу, которую кодировали углом в ноль градусов, и из-за ошибок, вызванных влиянием белого шума, эта величина будет отличаться от нуля.
5. Сравниваем принятые данные с переданными и сразу же
6. Считаем ошибки, и делать это будем при передаче каждого бита:
if (phaza > pi/2)||(phaza < -pi/2)
BER(n)=BER(n)+1;
endПри двоичной телеграфии, а это всё та же BPSK, ошибок не возникает до тех пор, пока отклонение угла не будет больше pi/2 в ту или другую сторону, и если это произошло, будем увеличивать счётчик ошибок при заданном EbN0 с номером n, а результат складывать в BER с номером n.
Всё, закрываем циклы:
end
endНаша модель готова, осталось построить полученную зависимость.
7. Строим график полученной вероятности возникновения ошибок функцией semilogy():
semilogy(EbN0,(BER./NN)); grid; hold on;То есть по оси абсцисс откладываем отношение EbN0, а по оси ординат, количество ошибок, делённое на количество переданных бит BER./NN.
Чтобы себя проверить возьмём из учебника Дж. Прокис, Москва, «Радио и связь», 2000, формулу 5.2.5 страница 217 для нашего случая и построим для сравнения:
semilogy(EbN0,1/2*(erfc(sqrt(10.^(EbN0/10)))),'--k'); hold off;Можно также взять график из википедии, там она обозначена синим цветом.
Далее подписываем легенду и оси на графике:
legend(['Imitation';'Theory']);
ylabel('BER'); xlabel('E_b/N_0, dB');В результате увидим примерно следующую зависимость:

Как видим, результаты имитационного моделирования подтверждают теоретические выводы из учебника, а это значит модель, не смотря на краткость, адекватно описывает происходящие при передаче данных процессы. Поставленная цель достигнута. Надеюсь, модель будет полезна для изучения.
Ниже полный текст программы имитационной модели:
clear; clc; close all;
EbN0 = -5:5;
BER=zeros(1,length(EbN0));
mnozh = 10.^(EbN0/20);
NN = 1000*(EbN0-EbN0(1)+1);
sig = 1+1i*0;
tic;
for n = 1:length(EbN0)
for k = 1:NN(n)
shum = (randn(1,1)+1i*randn(1,1))/sqrt(2);
spec = fft(mnozh(n)*sig+shum);% 20*log10(std(mnozh(n)*sig)/std(shum))
phaza = angle(spec);
if (phaza > pi/2)||(phaza < -pi/2) BER(n)=BER(n)+1; end
end
end
toc;
semilogy(EbN0,(BER./NN)); grid; hold on;
semilogy(EbN0,1/2*(erfc(sqrt(10.^(EbN0/10)))),'--k'); hold off; %PSK
legend(['Imitation';'Theory']);
ylabel('BER'); xlabel('E_b/N_0, dB');В полном тексте присутствуют ещё две функции tic и toc, поставленные перед основным циклом и после него, позволяющие измерить время выполнения основного цикла программы. Результат измерения времени вычислений будет выдан в командное окно:
Elapsed time is 0.00596 seconds.
Что и будет сигналом завершения вычислений.
Если появятся вопросы в комментариях, постараюсь ответить.



