Привет, Хаброжители! Маркос Лопез де Прадо делится тем, что обычно скрывают, — самыми прибыльными алгоритмами машинного обучения, которые он использовал на протяжении двух десятилетий, чтобы управлять большими пулами средств самых требовательных инвесторов.Машинное обучение меняет практически каждый аспект нашей жизни, алгоритмы МО выполняют задачи, которые до недавнего времени доверяли только проверенным экспертам. В ближайшем будущем машинное обучение будет доминировать в финансах, гадание на кофейной гуще уйдет в прошлое, а инвестиции перестанут быть синонимом азартных игр.
Воспользуйтесь шансом поучаствовать в «машинной революции», для этого достаточно познакомиться с первой книгой, в которой приведен полный и систематический анализ методов машинного обучения применительно к финансам: начиная со структур финансовых данных, маркировки финансового ряда, взвешиванию выборки, дифференцированию временного ряда… и заканчивая целой частью, посвященной правильному бэктестированию инвестиционных стратегий.
Отрывок. Понимание риска стратегии
15.1. Актуальность
Инвестиционные стратегии часто реализуются с точки зрения позиций, которыми владеют до тех пор, пока не будет выполнено одно из двух условий: 1) условие выхода из позиции с прибылями (взятие прибыли) или 2) условие выхода из позиции с убытками (остановка убытка). Даже когда стратегия явно не объявляет остановку убытка, всегда существует неявный предел остановки убытка, при котором инвестор больше не может финансировать свою позицию (маржин колл) или несет ущерб, вызванный увеличением нереализованного убытка. Поскольку большинство стратегий имеют (явно или неявно) эти два условия выхода, имеет смысл моделировать распределение исходов посредством биномиального процесса. Это, в свою очередь, поможет нам понять, какие сочетания частоты ставок, рисков и выплат являются неэкономичными. Цель этой главы — помочь вам оценить, когда стратегия уязвима к небольшим изменениям в любой из этих величин.
Рассмотрим стратегию, которая производит n одинаково распределенных взаимно независимых ставок в год, где исход Xi ставки i ∈ [1, n] представляет собой прибыль π > 0 с вероятностью P [Xi = π] = p и убыток –π с вероятностью P [Xi = –π] = 1 – p. Вы можете представить p как точность бинарного классификатора, в котором утвердительный исход означает заключение ставки на возможность, а отрицательный исход означает пропуск возможности: истинные утверждения вознаграждаются, ложные утверждения наказываются, и отрицательные исходы (будь то истинные или ложные) выплат не имеют. Поскольку исходы ставок {Xi}i=1,...,n независимы, мы будем вычислять ожидаемые моменты в расчете на ставку. Ожидаемая прибыль от одной ставки составляет E[Xi] = πp + (–π)(1 – p) = π(2p – 1). Дисперсия составляет
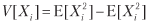, где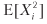 
= π2p + (–π)2(1 – p) = π2, следовательно, V [Xi] = π2 – π2 (2p – 1)2 = π2[1–(2p – 1)2] = 4π2p(1 – p). Для n одинаково распределенных взаимно независимых ставок в год среднегодовой коэффициент Шарпа (θ) равен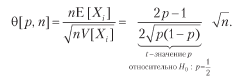 
Обратите внимание, как π уравновешивает приведенное выше уравнение, потому что выплаты симметричны. Так же как и в гауссовом случае, θ [p, n] можно понимать как решкалированное t-значение1. Этим иллюстрируется тот факт, что даже для малого
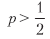коэффициент Шарпа может быть сделан высоким для достаточно большого n. Это служит экономической основой для высокочастотного трейдинга, где p может быть чуть выше .5, а залогом успешной биржевой деятельности является увеличение n. Коэффициент Шарпа является функцией от точности, а не от правильности, потому что пропуск возможности (отрицательное утверждение) не вознаграждается или наказывается напрямую (хотя слишком много отрицательных утверждений может привести к малому n, что будет сводить коэффициент Шарпа к нулю).Например, для
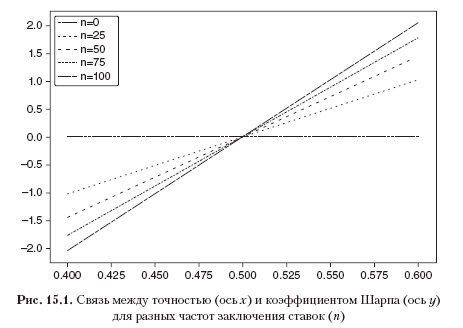
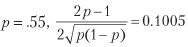и для достижения среднегодового коэффициента Шарпа, равного 2, требуется 396 ставок в год. Листинг 15.1 проверяет этот результат экспериментально. Рисунок 15.1 показывает коэффициент Шарпа как функцию от точности для разных частот ставок.Листинг 15.1. Коэффициент Шарпа как функция от числа ставок
out,p=[],.55
for i in xrange(1000000):
rnd=np.random.binomial(n=1,p=p)
x=(1 if rnd==1 else -1)
out.append(x)
print np.mean(out),np.std(out),np.mean(out)/np.std(out)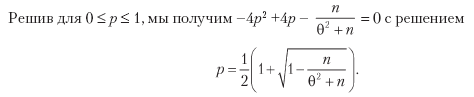
Это уравнение совершенно ясно выражает компромисс между точностью (p) и частотой (n) для заданного коэффициента Шарпа (θ). Например, для того чтобы давать среднегодовой коэффициент Шарпа, равный 2, стратегии, которая производит только еженедельные ставки (n = 52), потребуется довольно высокая точность p = 0.6336.
15.3. Асимметричные выплаты
Рассмотрим стратегию, которая производит n одинаково распределенных взаимно независимых ставок в год, где исход Xi ставки i ∈ [1, n] равен π+ с вероятностью P [Xi = π+] = p, а исход π– (π– < π+) случается с вероятностью P[Xi = π_] = 1 – p. Ожидаемая прибыль от одной ставки составляет E[Xi] = pπ+ + (1 – p)π– = (π+ – π–)p + π–. Дисперсия составляет V[Xi] =, где
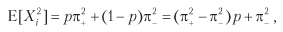
Наконец, мы можем решить предыдущее уравнение для 0 ≤ p ≤ 1 и получить
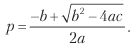
где:
a = (n + θ2)(π+ – π–)2;
b = [2nπ – θ2(π+ – π–)](π+ – π–);
Примечание: листинг 15.2 проверяет эти символические операции с помощью Python-овской оболочки SymPy Live, работающей на облачной службе Google App Engine: live.sympy.org.
Листинг 15.2. Использование библиотеки SymPy для символических операций
>>> from sympy import *
>>> init_printing(use_unicode=False,wrap_line=False,no_global=True)
>>> p,u,d=symbols('p u d')
>>> m2=p*u**2+(1-p)*d**2
>>> m1=p*u+(1-p)*d
>>> v=m2-m1**2
>>> factor(v)Приведенное выше уравнение отвечает на следующий вопрос: при заданном торговом правиле, характеризуемом параметрами {π–, π+, n}, какова степень точности p, необходимая для достижения коэффициента Шарпа, равного θ*? Например, для того чтобы получить θ = 2 для n = 260, π– = –.01, π+ = .005, нам потребуется p = .72. Благодаря большому числу ставок очень малое изменение в p (с p = .7 до p = .72) продвинуло коэффициент Шарпа с θ = 1.173 до θ = 2. С другой стороны, это также говорит нам о том, что данная стратегия уязвима для малых изменений в p. Листинг 15.3 реализует выведение предполагаемой точности. На рис. 15.2 показана предполагаемая точность как функция от n и π–, где π+ = 0.1, а θ* = 1.5. По мере того как для заданного n порог π– становится отрицательнее, требуется более высокая степень р, необходимая для достижения θ* для заданного порога π+. По мере того как для заданного порога π– число n становится меньше, требуется более высокая степень р, необходимая для достижения θ* для заданного π+.
Листинг 15.3. Вычисление предполагаемой точности
def binHR(sl,pt,freq,tSR):
´´´При заданном торговом правиле, характеризующемся параметрами {sl,pt,freq}, какова минимальная точность, требуемая для достижения коэффициента Шарпа, равного tSR?
1) Входы
sl: порог остановки убытка
pt: порог взятия прибыли
freq: число ставок в год
tSR: целевой среднегодовой коэффициент Шарпа
2) Выход
p: минимальная степень точности p, требуемая для достижения tSR
´´´
a=(freq+tSR**2)*(pt-sl)**2
b=(2*freq*sl-tSR**2*(pt-sl))*(pt-sl)
c=freq*sl**2
p=(-b+(b**2–4*a*c)**.5)/(2.*a)
return p
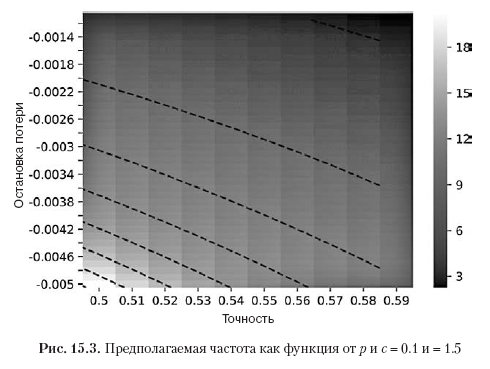
Листинг 15.4 решает θ[p, n, π–, π+] для предполагаемой частоты заключения ставок n. На рис. 15.3 показана предполагаемая частота в зависимости от p и π–, где π+ = 0.1, а θ* = 1.5. По мере того как для заданной степени p порог π– становится отрицательнее, требуется более высокое число n, необходимое для достижения θ* для данного порога π+. По мере того как для заданного порога π– степень p становится меньше, требуется более высокое число n, необходимое для достижения θ* для заданного порога π+.
Листинг 15.4. Вычисление предполагаемой частоты заключения ставок
def binFreq(sl,pt,p,tSR):
´´´При заданном торговом правиле, характеризующемся параметрами {sl, pt, freq}, какое число ставок в год необходимо для достижения коэффициента Шарпа tSR со степенью точности p?
Примечание: уравнение с радикалами, проверьте наличие постороннего решения.
1) Входы
sl: порог остановки убытка
pt: порог взятия прибыли
p: степень точности p
tSR: целевой среднегодовой коэффициент Шарпа
2) Выход
freq: число необходимых ставок в год
´´´
freq=(tSR*(pt-sl))**2*p*(1-p)/((pt-sl)*p+sl)**2 # возможно постороннее
if not np.isclose(binSR(sl,pt,freq,p),tSR): return
return freq
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 25% по купону — Машинное обучение
По факту оплаты бумажной версии книги на e-mail высылается электронная версия книги.
