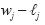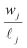Книга «Совершенный алгоритм. Жадные алгоритмы и динамическое программирование»

Привет, Хаброжители! В новой книге Тим Рафгарден рассказывает о жадных алгоритмах (задача планирования, минимальные остовные деревья, кластеризация, коды Хаффмана) и динамическом программировании (задача о рюкзаке, выравнивание последовательностей, кратчайшие пути, оптимальные деревья поиска). В данном посте представлен отрывок «Разработка жадного алгоритма»

Жадные алгоритмы, по всей видимости, хорошо подходят для задачи планирования работ, минимизируя взвешенную сумму сроков завершения. Выход имеет итеративную структуру, где работы обрабатываются по одной. Почему бы не использовать жадный алгоритм, который итеративно решает, какая работа будет следующей?

Первым шагом нашего плана является решение двух частных случаев общей задачи. Наши решения этих случаев покажут, как может выглядеть жадный алгоритм в общем случае. Затем мы сузим область до одного алгоритмакандидата и докажем, что именно этот кандидат решает задачу правильно. Процесс, с помощью которого мы приходим к этому алгоритму, более важен для запоминания, чем сам алгоритм; этот процесс является повторяемым, и вы можете его использовать в своих собственных приложениях.

13.3.1. Два частных случая

Давайте предположим, что для задачи минимизации взвешенной суммы сроков завершения на самом деле существует правильный жадный алгоритм. Как бы он выглядел, если исходить из того, что все работы имеют одинаковую длину (но, возможно, разные веса) или, напротив, имеют одинаковый вес (но, возможно, разную длину)?

УПРАЖНЕНИЕ 13.2

(1) если все длины работ являются идентичными, должны ли мы раньше планировать работы меньшего или большего веса?
(2) если все веса работ являются идентичными, должны ли мы раньше планировать более короткие или более длинные работы?
а) большего; короткие
б) меньшего; короткие
в) большего; длинные
г) меньшего; длинные
(Решение и пояснение см. в разделе 13.3.3.)

13.3.2. Дуэльные жадные алгоритмы

В общем случае работы могут иметь разный вес и разную длину. Всякий раз, когда наши два эмпирических правила — предпочитать более короткую работу и работу с бóльшим весом — на наше счастье для пары работ совпадают, мы знаем, какую из них запланировать первой (более короткую с бóльшим весом). Но что, если эти два правила дают противоречивый совет? Что мы должны делать с одной короткой работой с низким весом и одной длинной работой с высоким весом?

Каким будет самый простой жадный алгоритм, который сработает как надо? Каждая работа имеет два параметра, и алгоритм должен смотреть на оба. Наилучшим вариантом было бы разработать формулу, которая компилирует длину и вес каждой работы в единую отметку (вклад), вследствие чего планирование работ от самой высокой до самой низкой отметки гарантированно минимизирует сумму взвешенных сроков завершения. Если такая формула существует, то из наших двух частных случаев следует, что она должна иметь два свойства: (i) оставляя длину фиксированной, она должна увеличиваться от веса работы; (ii) оставляя вес фиксированным, она должна уменьшаться от длины работы (напомним, что чем выше отметки, тем лучше). Потратьте минуту на мозговой штурм нескольких формул, которые имеют оба этих свойства.


Пожалуй, самой простой функцией, которая увеличивается в весе и уменьшается в длине, является разница между ними:
предложение № 1 для отметки работы

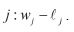
Указанная отметка могла бы быть отрицательной, но это не ставит никаких препятствий для последовательного выстраивания работ от самой высокой до самой низкой отметки. Существует, впрочем, немало других вариантов. Например, отношение двух параметров является еще одним кандидатом:

предложение № 2 для отметки работы

Эти две функции вычисления отметки приводят к двум разным жадным алгоритмам.

ЖАДНАЯ РАЗНОСТЬ GREEDYDIFF

Планировать работы в убывающем порядке
(произвольно разрывая совпадение значений).

ЖАДНОЕ ОТНОШЕНИЕ GREEDYRATIO

Планировать работы в убывающем порядке
(произвольно разрывая совпадение значений).

Таким образом, уже наше первое тематическое исследование иллюстрирует первую тему жадной парадигмы (раздел 13.1.2): предложить для задачи несколько соперничающих жадных алгоритмов обычно не составляет труда. Но какой из двух алгоритмов, если таковые имеются, является правильным? Быстрый способ исключить один из них — найти экземпляр, в котором два алгоритма выводят разные расписания с разными значениями целевой функции. В отношении любого алгоритма, результаты которого окажутся в этом примере хуже, мы можем заключить, что он не всегда является оптимальным. В двух частных случаях с работами одинакового веса или одинаковой длины оба алгоритма поступают правильно. Простейшим возможным примером исключения одного из них может быть экземпляр задачи, в которой две работы имеют разные веса и длины, вследствие чего оба алгоритма планируют работы в противоположных порядках. То есть мы ищем две работы, порядок которых по разнице является противоположным их порядку по отношению. Пример:


Первая работа имеет большее крупное отношение но большую разность (–2 против –1). Таким образом, алгоритм GreedyDiff планирует вторую работу первой, тогда как алгоритм GreedyRatio планирует противоположное.

УПРАЖНЕНИЕ 13.3

Какова сумма взвешенных сроков завершения в расписаниях, выводимых соответственно алгоритмами GreedyDiff и GreedyRatio?

а) 22 и 23
б) 23 и 22
в) 17 и 17
г) 17 и 11
(Решение и пояснение см. в разделе 13.3.3.)

Мы продвинулись вперед, исключив алгоритм GreedyDiff из дальнейшего рассмотрения. Однако результат упражнения 13.3 не ведет непосредственно к тому, что алгоритм GreedyRatio всегда будет оптимальным. Насколько нам известно, существуют другие случаи, когда этот алгоритм выдает неоптимальное расписание. Вы всегда должны скептически относиться к алгоритму, который не сопровождается доказательством его правильности, даже если этот алгоритм поступает правильно в нескольких тестовых примерах и крайне скептически относится к жадным алгоритмам.

В нашем случае алгоритм GreedyRatio, по сути, гарантированно будет минимизировать сумму взвешенных сроков завершения.

Теорема 13.1 (правильность алгоритма GreedyRatio). Для каждого множества положительных весов работ и положительных длин работ алгоритм GreedyRatio выводит расписание с минимально возможной суммой взвешенных сроков завершения.

Это логическое утверждение не является очевидным, и вы не должны доверять ему, не получив доказательств. В соответствии с третьей темой жадной парадигмы (раздел 13.1.2) это доказательство занимает весь следующий раздел.

О ЛЕММАХ, ТЕОРЕМАХ И Т. П.

В математической записи самые важные технические высказывания имеют статус теорем. Лемма — это техническое высказывание, которое помогает с доказательством теоремы (во многом как подпрограмма помогает с реализацией более крупной программы). Следствие — это высказывание, которое непосредственно вытекает из уже доказанного результата, например, частного случая теоремы. Мы используем термин «утверждение» (в иных источниках оно именуется пропозицией или высказыванием) для автономных технических высказываний, которые сами по себе не особенно важны.

Оставшейся темой жадной парадигмы является простота анализа времени выполнения (раздел 13.1.2). Здесь это, безусловно, так. Алгоритм GreedyRatio всего лишь сортирует работы по отношению, что занимает O (n log n) времени, где n — это число работ на входе (см. сноску 1 на с. 24).

13.3.3. Решения упражнений 13.2–13.3

Решение упражнения 13.2

Правильный ответ: (а). Сначала предположим, что все n работ имеют одинаковую длину, допустим, 1. Тогда каждое расписание имеет точно такое же множество сроков завершения — {1, 2, 3, ..., n} — и единственный вопрос состоит в том, какая работа получает срок завершения и каков этот срок. Наша семантика для весов работ, безусловно, предполагает, что работы с большим весом должны получать меньшие сроки завершения, и это действительно так. Например, вы бы не захотели запланировать работу с весом 10 третьей (со сроком завершения 3) и работу с весом 20 пятой (со сроком завершения 5); вам было бы лучше поменять позиции этих двух работ, что уменьшило бы сумму взвешенных сроков завершения на 20 (как вы можете убедиться сами).

Второй случай, в котором все работы имеют одинаковый вес, немного тоньше. Здесь вы хотите отдать предпочтение более коротким работам. Например, рассмотрим две работы единичного веса с длинами 1 и 2. Если вы сначала запланируете более короткую работу, то сроки завершения составят 1 и 3 при суммарном 4. В обратном порядке сроки завершения составят 2 и 3 с худшим итогом 5. В общем случае запланированная работа сначала вносит вклад в сроки завершения всех работ, так как все работы должны ждать завершения первой. При прочих равных условиях планирование самой короткой работы сначала минимизирует это негативное влияние. Вторая работа вносит свой вклад во все сроки завершения, кроме первой работы, поэтому вторая самая короткая работа должна быть запланирована следующей, и т. д.

Решение упражнения 13.3

Правильный ответ: (б). Алгоритм GreedyDiff планирует вторую работу первой. Срок завершения этой работы составляет тогда как срок завершения другой работы составляет Сумма взвешенных сроков завершения тогда составит


Алгоритм GreedyRatio планирует первую работу первой, в результате приходя к срокам завершения
и сумме взвешенных сроков завершения, равной


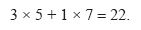
Поскольку для этого примера алгоритму GreedyDiff не удается вычислить оптимальное расписание, он не всегда является правильным.

» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок

Для Хаброжителей скидка 25% по купону — Алгоритмы

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.