Лучший способ выбора случайной точки в круге

Допустим, вам нужно найти случайную точку с равномерным распределением в круге. Как же это сделать лучше всего? Когда я впервые начал изучать эту задачу, я работал над программным проектом, требовавшим случайного распределения значений в круге, но довольно быстро я спустился в неожиданно глубокую кроличью нору, заполненную любопытной математикой, поэтому решил объединить все свои находки в одну статью.

Прежде чем переходить к кругу, давайте упростим задачу и выберем случайную точку внутри квадрата. Для этого достаточно выбрать случайные координаты и в пределах квадрата. В некоторых случаях этот принцип можно применить и к кругам. Например, точка может попадать в круг, но не всегда, поэтому нам нужен дополнительный этап — если выбранная точка находится за границами круга, то мы пробуем снова и снова, пока точка не окажется в круге. Этот процесс является примером выборки с отклонением (rejection sampling) — вместо того, чтобы преобразовать некое распределение, мы просто отклоняем все результаты, находящиеся вне нужного нам интервала.

Способ вполне рабочий, но мне не совсем нравится то, что этот алгоритм иногда приходится исполнять множество раз. Предположим ради простоты, что радиус нашей окружности равен (но дальнейшие вычисления применимы к кругам любого радиуса). Вероятность того, что выбранная этим алгоритмом точка находится внутри круга, равна площади круга, разделённой на площадь квадрата, или , делённая на , что приблизительно равно . Это значит, что вероятность выбора алгоритмом неправильной точки раз равна в степени , где — некое положительное число. С увеличением это значение очень быстро становится очень малым. Вероятность четырёхкратного неправильного срабатывания алгоритма меньше четверти процента. Мы можем вычислить среднее количество необходимых попыток, или ожидаемое значение , которое обратно коэффициенту успешного выбора, то есть , что приблизительно равно . То есть в среднем нам достаточно будет сделать только одну попытку. Все эти вычисления дают нам понять, что не стоит беспокоиться о слишком долгом повторении процесса.

Давайте реализуем алгоритм на Python.

def rejection_sampling():
    while True:
        x = random() * 2 - 1
        y = random() * 2 - 1
        if x * x + y * y < 1:
            return x, y

Если я выполню эту функцию красивое количество раз (), то получу желаемый результат — точки случайно, но равномерно распределены по кругу.


На этом можно было бы и остановиться, но мы можем сделать так, чтобы подходящая точка гарантированно выбиралась с первого раза. Проблема в том, что мы используем неправильную систему координат (декартову), которая ограничивает нас, заставляя выбирать два значения, представляющие собой расстояния на перпендикулярных осях, которые мы называем и . Гораздо больше нашим целям подойдёт полярная система координат, в которой точки задаются расстоянием от точки начала координат и углом. Например, рассмотрим точку (, ). 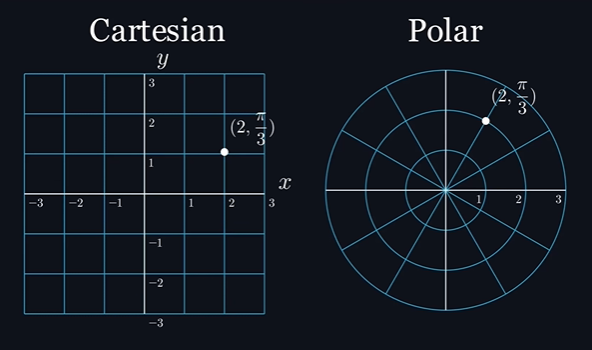В декартовых координатах это будет точка на пересечении и , но в полярных координатах это будет точка, расположенная в двух единицах от точки начала координат и повёрнутая на угол радиан.


Достаточно взглянуть на графическое представление этих систем координат, чтобы понять, почему полярная система координат больше подходит для работы с кругами. Итак, всё, что нам нужно сделать — выбрать случайный радиус в интервале от 0 до 1 и случайный угол (тета) от до . Для отрисовки эти координаты необходимо будет преобразовать обратно в декартовы, что можно сделать, умножив на косинус или синус для получения, соответственно, координат и


Реализация этого алгоритма на Python содержит случайную переменную от до и случайную переменную от до , а возвращает , умноженный на косинус и , умноженный на синус .

def random_polar():
    theta = random() * 2 * pi
    r = random()
    return r * cos(theta), r * sin(theta)

Если мы снова выполним этот алгоритм 3141 раз, результаты должны выглядеть похожими на алгоритм выборки с отклонением… но это не так.


Как видите, точки гораздо плотнее располагаются в центре круга. Давайте разберёмся, почему. Мы знаем, что проблема не в генерировании , потому что точки равномерно распределены по кругу, поэтому виноват должен быть способ выбора значения . Используемый нами генератор случайных чисел имеет равномерное распределение, то есть вероятность выбора каждого возможного радиуса одинакова. Из этого следует, что каждое кольцо в круге в среднем будет содержать одинаковое количество точек. Возможно, вы уже видите в чём проблема — с увеличением длины окружности кольца количество точек остаётся постоянным, то есть в наружных кольцах с большим радиусом точки имеют меньшую плотность, чем во внутренних.


Мы можем описать процесс выбора радиуса или значения при помощи функции плотности вероятности (probability density function, PDF) — функции, интеграл которой сообщает нам вероятность попадания непрерывной случайной переменной в заданный интервал. Сейчас график этой функции является горизонтальной линией от до , поскольку вероятность выбора каждого значения одинакова.


Итак, мы знаем, что эта PDF нам не подходит. Давайте выясним, как она должна выглядеть для того, чтобы точки были равномерно распределены в круге. Так как длина окружности линейно зависит от радиуса, для сохранения одинаковой плотности точек их количество должно тоже линейно зависеть от радиуса. Следовательно, наша PDF должна быть линейной функцией, которую мы обозначим как , где — некий наклон. Но как нам вычислить значение ? Вероятность того, что выбранное значение будет находиться в интервале от до , равна 100% или . Следовательно, интеграл или площадь под кривой нашей PDF от до тоже должна быть равна . Из этого мы можем вычислить высоту треугольника, а затем вычислить наклон гипотенузы, или составить интеграл. Именно так я и сделаю. При решении интеграла выясняется, что наклон нашей PDF равен , то есть её уравнение имеет вид .


Любопытно то, что каждая PDF имеет интеграл , то есть этот трюк будет срабатывать всегда. Теперь когда мы знаем, как должно выглядеть распределение, можно реализовать его при помощи одного генератора равномерно распределённых случайных чисел. Необходимо найти преобразование, применив которое к равномерному распределению, можно получить нужное нам линейное распределение. Для начала давайте создадим функцию распределения (cumulative distribution function, CDF), которую я обозначу как . Она представляет собой интеграл PDF, который в нашем случае равен . CDF обозначает вероятность того, что случайная переменная будет меньше или равна аргументу функции.


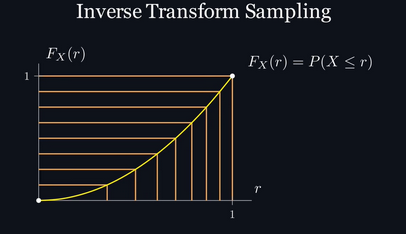
При помощи этой CDF мы можем воспользоваться стратегией под названием «метод обратного преобразования» (inverse transform sampling): берётся равномерное распределение, например, распределение нашего генератора случайных чисел, и преобразуется так, что хотя наша случайная переменная x не будет иметь равномерного распределения, сами вероятности, отложенные на оси y, будут им обладать. Давайте посмотрим, что произойдёт, если мы возьмём эти вероятности в качестве аргумента функции, по сути получив функцию, обратную нашей CDF. Если мы возьмём какое-то число из равномерно расположенных значений , и посмотрим на соответствующие им значения , то увидим, что получим нужный результат там, где точки более плотно расположены при больших значениях и более рассеяны при меньших значениях.


Такое понимание уже достаточно ценно, но я покажу вам более строгое доказательство того, что подстановка случайной переменной с равномерным распределением в функцию, обратную нашей CDF, даст нужное нам распределение. Пока мы знаем, что CDF обозначает вероятность того, что случайная переменная будет меньше или равна аргументу функции , но давайте вернёмся к тому, как выглядит PDF равномерного распределения. Я обозначу случайную переменную с равномерным распределением от до как . График — это горизонтальная линия от до при равном . Следовательно, уравнение CDF (интеграл PDF) будет . Из определения CDF следует, что вероятность того, что будет меньше или равна , равна . Если мы подставим вместо , то становится ясно, что вероятность того, что значение случайной переменной с равномерным распределением будет меньше или равно , равно , потому что оно находится посередине между и . Вернувшись к методу обратного преобразования, мы можем сказать, что равна вероятности того, что будет меньше или равна . Теперь мы можем применить к обоим сторонам неравенства значение, обратное нашей CDF, что даст нам два неравенства, меньших или равных . Следовательно, , случайная переменная с нужным нам распределением, равна обратному значению CDF, применённому к случайной переменной с равномерным распределением, а мы знаем, что функция, обратная CDF, — это . Давайте реализуем всё это на Python.

def sqrt_dist():
    theta = random * 2 * pi
    r = sqrt(random())
    return r * cos(theta), r * sin(theta)

Единственное отличие между этой и предыдущей функциями заключается в том, что для вычисления я теперь беру квадратный корень случайного числа. Снова выполнив алгоритм 3141 раз, мы опять увидим, что точки равномерно распределились по кругу.


Итак, теперь у нас есть два приемлемых способа выбора случайной точки с равномерным распределением внутри круга, но давайте не будем останавливаться. Существует и ещё один очень любопытный способ, приводящий точно к такому же результату.

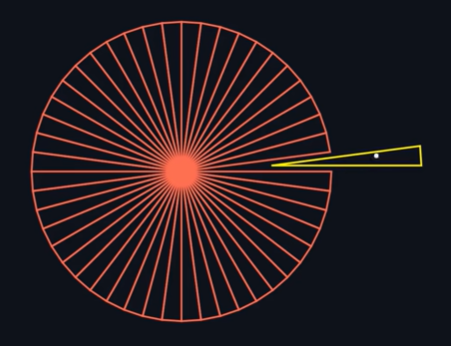
Круг можно рассматривать как набор бесконечного множества бесконечно узких равнобедренных треугольников, повёрнутых относительно точки. Поэтому мы можем выбрать случайный треугольник, а затем выбрать в этом треугольнике случайную точку, чтобы получить случайную точку с равномерным распределением в круге.


Давайте вернёмся к тому, как мы выбирали случайную точку в квадрате — этот способ можно применить и к параллелограммам. Так как мы имеем дело с равнобедренными треугольниками, воспользуемся ромбом, который, как известно, состоит из двух равнобедренных треугольников, соединённых основаниями. Просто выберем случайную точку на двух соседних сторонах, а затем из каждой точки проведём линию, параллельную соседней стороне, и найдём точку их пересечения. Чтобы ограничить интервал только треугольником, мы можем провести диагональ и отражать все точки, попавшие не в ту часть ромба. Давайте обозначим четыре вершины ромба как , , и , две случайные точки на соседних сторонах и , а выбранную точку . Так как треугольники бесконечно тонкие, угол при вершине будет стремиться к нулю, и при этом высота ромба тоже будет стремиться к нулю. Это значит, что все его стороны, по сути, становятся параллельными. Следовательно, расстояние от центральной точки до выбранной точки равна сумме и .


Теперь мы при необходимости сможем отразить точку относительно диагонали, которая находится посередине между точками и .


Всё это уже можно преобразовать в код на Python. Во-первых, вычисляется как обычно, но это также можно рассматривать как выбор случайного треугольника, так как они бесконечно тонкие, поэтому каждый треугольник получает собственный угол. Затем сложением двух случайных величин и вычисляется . Если больше или равен единице, это значит, что точка находится с неправильной стороны ромба и вычисляется значение её отражения вычитанием . Конструкция остаётся такой же.

def sum_dist():
    theta = random() * 2 * pi
    r = random() + random()
    if r >= 1:
        r = 2 - r;
    return r * cos(theta), r * sin(theta)

Мы снова выполним алгоритм 3141 раз и получим равномерное распределение точек по кругу.

Однако у меня возник вопрос: почему сложение двух случайных величин не равно умножению одной случайной переменной на два? Проще всего рассуждать над этим вопросом на примере игровых костей. Если мы возьмём результат броска одной честной кости и умножим его на два, то увидим, что возвращаются только чётные числа и что кость имеет равномерное распределение. Однако если сложить результаты двух честных костей, то можно увидеть, что вероятность результата выше, чем вероятность любого другого числа, потому что получить сумму на двух костях можно шестью разными способами. Сумму же и можно получить только одним способом, из-за чего их вероятность становится ниже. Если мы составим график частоты каждого возможного результата, то при приближении суммы к , что является средним и , частоты сумм увеличиваются.


Если мы представим, что отражаем правую половину графика, результат будет выглядеть очень похожим на желаемую PDF, но на этом я заметил кое-что странное. Оба этих способа вычисляют как квадратный корень от случайного числа, а отражение суммы двух случайных чисел должно иметь то же распределение с линейной PDF, равной и квадратной CDF . Поначалу это кажется неправильным: как эти две кажущиеся не связанными друг с другом и совершенно разные функции могут иметь одинаковое распределение? Мы знаем, что распределение способа с квадратным корнем правильное, ведь мы вывели его непосредственно из нужной CDF. Давайте докажем распределение способа с суммами.

К счастью, уже существует распределение Ирвина-Холла, сообщающее нам распределение суммы равномерно выбранных случайных чисел от 0 до 1. В нашем случае . Вот уравнения для PDF и CDF.


Можно использовать их, но на самом деле это необязательно, потому что существует очень изящный геометрический вывод, хорошо работающий с низкими значениями . Для начала полезно будет отложить две переменные и на осях и , чтобы лучше их визуализировать. Можно начертить линию, представляющую все возможные способы суммирования и для получения некого числа от до . Уравнение прямой будет иметь вид . Длина этой линии будет пропорциональна PDF, возрастающей в интервале от до и снижающейся в интервале от до . Площадь под этой прямой и в границах этого единичного квадрата представляет собой CDF.


Но нужно помнить о том, что любое значение от до отражается и даёт нам значение . Это значит, что CDF всегда можно представить как площадь треугольника с основанием и высотой , то есть . Однако поскольку все точки в этом треугольнике по сути удваиваются в результате отражения, эту площадь нужно умножить на и получить нужную нам CDF ().


Но зачем останавливаться на этом? Любая функция, имеющая такое распределение, теоретически должна выбирать значение , генерирующее случайную точку с равномерным распределением внутри круга.

Я покажу вам ещё один способ, но призываю вас попробовать найти собственный, поскольку я перечислил далеко не все варианты. В этом последнем способе выбор значения выполняется взятием максимума от двух случайных переменных. Я не использую встроенную в Python функцию , поскольку её производительность ниже того, что вы видите в моём коде.

def max_dist():
    theta = random() * 2 * pi
    r = random()
    x = random()
    if x > r:
        r = x
    return r * cos(theta), r * sin(theta)

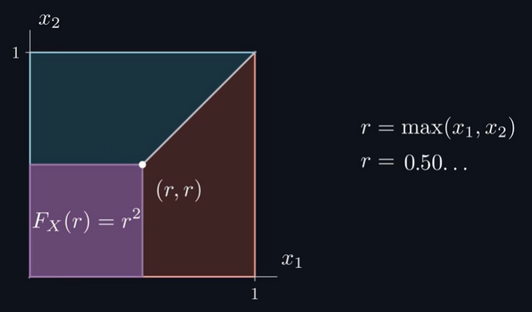
Мы снова равномерно распределим 3141 точку в круге, но это нужно доказать. Доказательство выполняется схожим с распределением Ирвина-Холла способом — откладыванием величин и . Как и ранее, поскольку равен их максимуму, мы можем разделить квадрат по диагонали. Любая точка, оказавшаяся в красной половине квадрата, возвращает , потому что он больше . Любая точка, оказавшаяся в синей половине квадрата, аналогично возвращает . CDF представлена квадратом с длиной стороны , в котором каждая точка и меньше или равна , а площадь квадрата снова даёт нам CDF, равную .


После разбора этих четырёх способов нам осталось протестировать их, чтобы узнать, какой выполняется быстрее всего. Выполнив каждую функцию 3 142 592 раза, мы получили такие значения времени:


По увеличению скорости выполнения: первый способ (rejection_sampling), четвёртый (max_dist), второй (sqrt_dist) и третий (sum_dist)

Значительно быстрее остальных оказалась выборка с отклонением (rejection sampling), и это логично, потому что остальные три способа содержат дополнительные затраты на выполнение операций синуса и косинуса. Значит ли это, что бОльшая часть нашей работы была проделана напрасно и что нам нужно было остановиться раньше? Я так не считаю, потому что если бы не эта задача, мне никогда бы не довелось познакомиться с PDF и CDF, да и с целым множеством интересных геометрических доказательств.