
Мне доводилось принимать участие в упражнениях с Матрицей рисков компании.
Действие происходило в три этапа. Первый: мальчики и девочки анкетировали вопросами типа «перестал ли ты пить коньяк по утрам», на которые надо отвечать только «да» или «нет».
На втором этапе показывалась «научно-обоснованная» матрица рисков.
На перманентном третьем этапе все подразделения той компании пытались из года в год сдвинуться на более низкие позиции на матрице, но это удавалось только за счет личного обаяния. Те же, кто не смог сдвинуться становились крайними по любой неудаче бизнеса.
Инстаграм
Вот типовая Матрица рисков, которую предлагает Гугл.

Для примера в Интернете найдена случайная Матрица рисков из очень старого отчета.
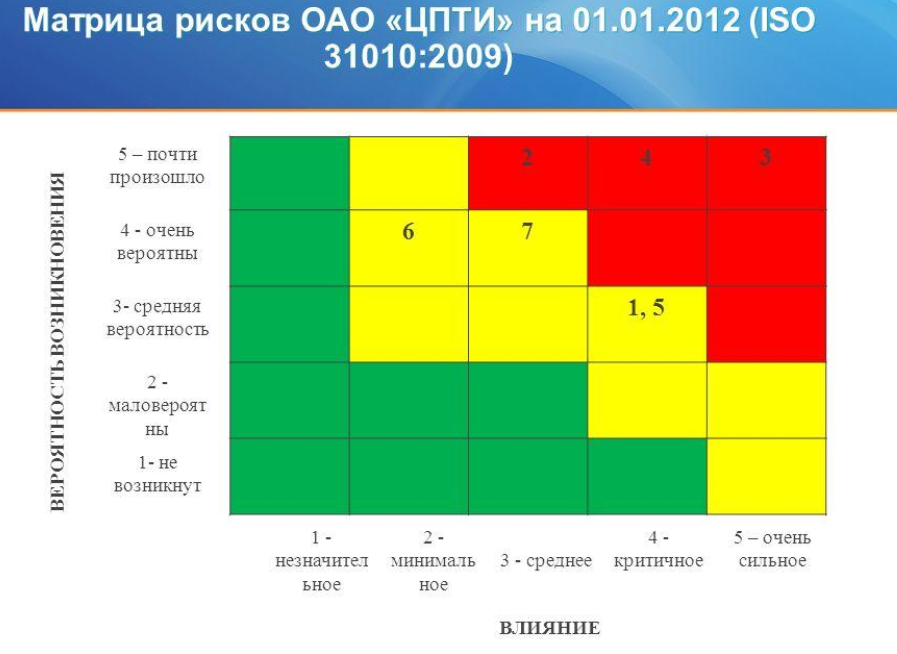
Числа внутри цветных прямоугольников означают содержательную интерпретацию риска, которая пока не очень нужна. Описание риска очень широко и размыто. Не верится, что все компоненты описания по отдельности и вместе дают единственное число в очень узком диапазоне.
Если следовать типовой матрицы Гугл, то всем содержательным описаниям «вероятность» и «влияние» можно поставить в соответствие конкретные числа.
Вот модернизированная матрица исходной.

Она не очень удобна для работы, так как симметрична относительно дополнительной, а не главной диагонали.
Возможно, что Матрица рисков в такой форме более удобна для менеджеров. Её перестройка с симметрией относительно главной диагонали не меняет сути матрицы. Кроме того, всегда можно сделать шаг назад и вернуться к исходному представлению.
Перестроение матрицы происходит путём замены порядка строк на обратный (симметрия относительно вертикальной центральной оси). В результате получена матрица симметричную относительно главной диагонали.

Эти же преобразования для исследуемой Матрицы рисков.

Числа, отличные от 0 — это номер риска, связанный в итоге с неким структурным подразделением. Эта кодировка имеет место только в связи с бюрократической иерархией в компании, а не с рисками. Например, для элемента {1,5}. В плане риска ситуация ничем не будет отличаться, если совместить описания риска1 и риска5. Если это разные риски, то можно уменьшить шаг матрицы и поместить риск в более подходящую позицию.
В итоге преобразования должны приводить к тому, что каждый различный риск является отдельным элементом.
Позиция [1,3] в стандартной системе нумерации матриц означает элемент, находящийся на пересечении 1-ой строки и 3-го столбца. Для рассматриваемой матрицы в позиции [1,3] стоит число 2. Это означает, что если имеет место шкала с максимальным значением «5 — почти произошло» (1.), то в [1,3] ожидаем «3 — среднее» (0.6) влияние. Пусть «влиянию» в таргитируемом промежутке соответствует определенный ущерб (damage): 5-d5, 4-d4, 3-d3, 2-d2,1-d1. Тогда, если за определенный период имело место 1 происшествие из группы 2, то ущерб составит 1.*0.6*d3*1, а если за этот же период произошло n происшествий из группы 2, то ущерб составит 1.*0.6*d3*n
Тогда исследуемая матрица примет вид.

Проводится еще одно преобразование: транспонирование путём перемены мест столбцов и строк.

Нижняя строка легенды становится излишней, так как соответствующая вероятность учтена в значениях матрицы. Первый вертикальный столбец также учтен в значениях матрицы, но он важен тем, что задает структуру событий, которые можно фиксировать или прогнозировать за некий период. Имея вектор-столбец из количества событий, относящихся к соответствующему типу (очень сильное, критическое,…) можно стандартным образом умножать матрицу на вектор-столбец и получать структурированный размер ущерба.
Без легенды матрица будет выглядеть так.

Первая основная задача.
Получив матрицу А можно приступать к решению первой основной задачи: при известном количестве и качестве произошедших событий вычислить размер ущерба.
Пусть за определенный период произошло 2 — «очень сильных» событий, 3 — «критичных», 1 — «среднее», 5 — «минимальных» и 7 — «незначительных». Умножив матрицу А на вектор количества событий получаем структуру ущерба.

Общий ущерб.

Теперь можно проверять точность оценок, вносить коррективы, оценивать возможные варианты сокращения размера ущерба.
Приведенные трансформации исходной матрицы были проведены, чтобы получить простую вычислительную процедуру ущерба. От матрицы А всегда можно однозначно вернуться к исходной матрице.
Алгебро-философский рубеж.
Для каждой квадратной матрицы имеется однозначное линейное преобразование, соответствующее этой матрице. Обозревая матрицу сложно понять какое линейное преобразование стоит за ней. Кроме того, неизвестно в каком базисе произведено матричное представление.
Матрица риска — квадратная матрица и ей должно соответствовать некое линейное преобразование. Этот факт не зависит от способа получения матрицы и идей реализованных в нем.
Важно, чтобы определитель матрицы не равнялся нулю. Это требования метода, обеспечивающего каноническое представление матрицы.
Далее показывается, что не просто ограничение метода, а требование отвечающее потребностям практики.
Рассматриваемая Матрица рисков имеет две нулевых строки и один нулевой столбец. В любом случае определитель этой матрицы будет равняться нулю. Ниже приведен рисунок, показывающий как компания намерена снижать риски.

Стрелками показано как будут снижаться риски. Каким образом — не важно, важно, что при этом новая ситуация опять представляется матрицей. Этой матрице соответствует некое линейное преобразование. Плюс переход от «старой» матрицы к «новой» — это матрица и линейное преобразование.
Что означает ненулевой определитель? Это возможность шагать «вперед-назад». Если определитель нулевой, то шага «назад» сделать нельзя.
При этом матрица снижения рисков изначально связана со «старой» матрицей. То есть на картинке можно и нужно парить «вперед-назад», а в формализованном варианте шагать «вперед-назад» нельзя.
Следующая проблема связана с тем, что большой риск с малой вероятностью может быть сопоставим с риском от очень большого количества малых рисков с малой вероятностью.
В приведенном выше примере 7 незначительных событий формально не вызывают никакого ущерба. Понятно, что это не так. Отсутствие малых рисков только подчеркивают недостаточную некорректность формирования Матрицы рисков.
Пусть определитель Матрицы рисков не равен нулю и это следствие преемственности работ по снижению рисков, а не искусственное для бизнеса требование метода.
Итак, имеются: Матрица рисков, которая соответствует неизвестному линейному преобразованию и неизвестному базису; определитель Матрицы, который не равен нулю.
Что можно сделать? Привести Матрицу рисков к каноническому виду с понятным ортонормированным базисом.
В работе Александра Емелина дается следующее аллегорическое описание преимуществ канонического вида. “Предположим, что есть листок бумаги, на котором написано некоторое слово. Но он сложен так, что слова не видно. После канонического преобразования листок разворачивается таким образом, что слово можно увидеть. Если используется ортонормированный базис, то листок бумаги останется того же размера.”
Вторая основная задача. Каноническое представление.
В рассматриваемую матрицу добавляются элементы так, чтобы определитель не равнялся нулю. Чтобы избежать слишком больших формул значения округляются.

Далее по стандартной схеме матрица приводится к каноническому виду.
Собственные значения Матрицы рисков.

Дальнейшая работа с символическими значениями будет тяжёлой при ортогонализации и результат будет невозможно визуализировать (очень громоздкие символические матрицы).
Пусть (для примера) d1=1, d2=2, d3=5, d4=8, d5=12.
Тогда Матрица рисков М принимает вид.

Проверяется, что определитель М не равен нулю.
Вычисляются собственные значения.

Находится матрицу из собственных векторов.

Она ортогонализируется. Получается матрица ORT ортонормированных векторов.

Для проверки первый вектор (столбец) умножается попарно на все остальные.

В новом базисе находится представление исходного линейного преобразования (определяющего Матрицу рисков) в переменных z1, z2, z3, z4, z5.

Если пренебречь очень маленькими слагаемыми, то получается каноническое представление линейного преобразования.

Причем коэффициенты при квадратах соответствуют ранее вычисленным собственным значением.
Новый вид Матрицы рисков в ортонормированном базисе.

Практическая польза канонического представления.
Что можно сказать про исходную Матрицу рисков?
Она представляет неизвестное линейное преобразование.
Её строки обозначаются (сверху-вниз) как x1, x2, x3, x4, x5. Строки Матрицы рисков представляют разложение по неизвестному базису.
Так
x1=10*d5*b1+0*b2+0*b3+0*b4+0*b5,
x2= 8*d4*b1+0*b2+4*d4*b3+0*b4+0*b5, и так далее.
Наличие ортонормированного базиса обеспечивает свободу хождения между переменными X и Z.
В переменных Z явно видна функция линейного преобразования, которая в исходной Матрице рисков была непонятной.
Явная польза от канонического вида состоит в возможности корректировки типа угроз. Если изначально классификация шла по шагу в 20%, то теперь ее можно пересмотреть пересчитав значения концов диапазонов в новом базисе. Останется также 5 типов событий, но шаги между ними будут разными.
Фактически новая форма позволяет Матрице рисков уйти от роли «жупела» и стать нормальным инструментом цифрового управления бизнесом. Одним из многих.





