Моделирование двумерной модели Изинга на языке C++ (с применением графического пакета OpenGL)

Модель Изинга

Модель Изинга была введена для понимания природы ферромагнетизма и повлияла на изучение фазовых переходов и критических явлений. Ферромагнетизм описывает появление самопроизвольной намагниченности у ферромагнетиков ниже определенной температуры — точки Кюри. В точке Кюри (узкой области температур) происходит упорядочение, в данном случае, выстраивание магнитных моментов, которое влечет фазовый переход, то есть свойства вещества меняются скачком.

Изначально модель была предложена В. Ленцем в 1920 году, и исследована Изингом для одномерного случая, в честь чего и получила свое название. В данной модели, каждая вершина кристаллической решетки принимает число: +1 или -1, — поле «вверх» или «вниз». Число, которое ставится в соответствие вершинам, называется спин. Таким образом, решетка из N числа спинов может находиться в 2^N состояниях. Каждому состоянию соответствует энергия, которая получается из попарного взаимодействия спинов соседних атомов:



Где J — энергия взаимодействия соседних спинов (константа обменного взаимодействия одна и та же для всех пар), s_i и s_j — спины.

При этом J > 0 описывает поведение ферромагнетика, J < 0 антиферромагнетика.

Если поместить модель во внешнее магнитное поле H, то полная энергия примет вид:



Суммарный магнитный момент или намагниченность определяется по следующей формуле:

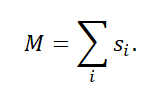
Метод Монте-Карло

Как упоминалось ранее, всего возможно 2^N состояний и при достаточно большом числе спинов N трудно получить численные результаты. Например при N=10 получим 2¹⁰ состояний, которые напрямую смоделировать не так просто, поэтому для моделирования используется статистический подход.

В этом подходе система рассматривается в состоянии термодинамического равновесия при определенной температуре T. В ходе обмена энергией с окружающей средой, энергия будет изменяться около равновесного состояния, а средняя энергия одной частицы пропорциональна T. Реализация постоянного случайного изменения вокруг состояния равновесия использует метод Монте-Карло и моделирование можно разделить на этапы:

1. Разыгрывать состояния α_i системы (например, случайным образом) при фиксированном T;
2. Считать для этих состояний термодинамические характеристики вблизи равновесия (энергию E, намагниченность M);
3. Усреднять полученные значения

Алгоритм Метрополиса.

В задачах статистической механики выражения «метод Монте-Карло» и «метод выборки Метрополиса» — почти синонимы. Приведем наиболее общую форму алгоритма Метрополиса на примере системы спинов или частиц:

1. Формируем начальную конфигурацию.
2. Производим случайное пробное изменение в начальной конфигурации. Например, выбираем случайным образом какой-нибудь спин и пробуем его опрокинуть. Или выбираем случайную частицу и пробуем переместить ее на случайное расстояние.
3. Вычисляем ∆Е, то есть изменение энергии системы, обусловленное произведенным пробным изменением конфигурации.
4. Если ∆Е меньше или равно нулю, то принимаем новую конфигурацию и переходим к шагу 8.
5. Если ∆Е положительно, вычисляем «вероятность перехода»:
   
   
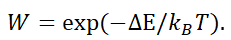
6. Генерируем случайное число rnd в интервале (0, 1)
7. Если rnd≤W, то новую конфигурацию принимаем, в противном случае сохраняем предыдущую конфигурацию.
8. Определяем значения требуемых физических величин.
9. Повторяем шаги 2–8 для получения достаточного числа конфигураций или «испытаний».
10. Вычисляем средние по конфигурациям, которые статистически независимы друг от друга.

Двумерная модель Изинга на языке C++

Напишем собственную программу, реализующую двумерную модель Изинга с помощью метода Монте-Карло и алгоритма Метрополиса. Реализуем следующий функционал:

• Пользователь задает размер стороны решетки SIZE, максимально допустимую температуру T_MAX.
• В окне ISING будет находиться вся решетка размером SIZE×SIZE, в решетке спины, которые будут направлены вверх (0), будут являться ячейками белого цвета, тогда как спины, направленные вниз (1), будут являться ячейками черного цвета.
• Пользователь может изменять температуру T с помощью красной шкалы справа в окне ISING. Пользователь может изменять температуру, используя нажатие мыши или кнопки W и S на клавиатуре (соответственно повышение и понижение температуры). Максимально допустимая температура определяется пользователем, минимально допустимая – 0,01℃.
• Белая черта на красной шкале – температура Кюри ферромагнетика Изинга. В двумерной модели Изинга при критической температуре T=2,269℃ происходит фазовый переход из неупорядоченного в упорядоченное ферромагнитное состояние.
• Изменение конфигурации будет происходить непосредственно на экране каждые 10 мс (миллисекунд); с каждым изменением конфигурации будет увеличиваться число шагов Монте-Карло.
• Пользователь может изменять температуру перед каждым новым изменением конфигурации решетки спинов.
• Каждые 10 с (секунд) будет происходить вывод данных в консоль (коэффициент принятия, средняя энергия на спин, средний квадрат энергии на спин, средняя намагниченность, средний квадрат намагниченности).

#include <iostream>
#include <random>
#include <locale>
#include "glut.h"

using namespace std;

#define SIZE 256
#define SIZE_PX 800
#define T_MAX 4
#define CURIE_SCALE 1000. 

double quadSize = SIZE_PX / (double)SIZE;

short lattice[SIZE][SIZE];
double w[5];
double T = T_MAX, M, E;

int ratio = 0;
size_t nmcs = 0;
double ecum = 0, e2cum = 0, mcum = 0, m2cum = 0;

void display()
{
	glClear(GL_COLOR_BUFFER_BIT);
	
	glBegin(GL_QUADS);
	for (int i = 0; i < SIZE; i++)
		for (int j = 0; j < SIZE; j++)
		{
			glColor3f(lattice[i][j], lattice[i][j], lattice[i][j]);
			glVertex2d(i, j);
			glVertex2d(i, j + 1);
			glVertex2d(i + 1, j + 1);
			glVertex2d(i + 1, j);
		}
	glEnd();

	glBegin(GL_QUADS);
	{
		glColor3f(1, 0, 0);
		glVertex2d(SIZE, 0);
		glVertex2d(SIZE, SIZE * T / T_MAX);
		glVertex2d(SIZE + SIZE / 8, SIZE * T / T_MAX);
		glVertex2d(SIZE + SIZE / 8, 0);

		glColor3f(1, 1, 1);
		glVertex2d(SIZE, SIZE * 2.27 / T_MAX - SIZE / CURIE_SCALE);
		glVertex2d(SIZE, SIZE * 2.27 / T_MAX + SIZE / CURIE_SCALE);
		glVertex2d(SIZE + SIZE / 8, SIZE * 2.27 / T_MAX + SIZE / CURIE_SCALE);
		glVertex2d(SIZE + SIZE / 8, SIZE * 2.27 / T_MAX - SIZE / CURIE_SCALE);
	}
	glEnd();

	glutSwapBuffers();
	glFlush();
}

void calcW()
{
	double e4 = exp(-4 / T), e8 = e4 * e4;
	w[0] = w[4] = e8;
	w[1] = w[3] = e4;
	w[2] = 0;
}

void init()
{
	M = E = 0;
	static std::default_random_engine generator;
	std::uniform_int_distribution<int> distribution(0, RAND_MAX);
	for (int i = 0; i < SIZE; i++)
		for (int j = 0; j < SIZE; j++)
		{
			lattice[i][j] = ((distribution(generator) / (double)RAND_MAX >= 0.5) - 1) * 2 + 1;
			M += lattice[i][j];
		}

	for (int i = 0; i < SIZE; i++)
		for (int j = 0; j < SIZE; j++)
		{
			E += (i + 1 != SIZE) ? lattice[i][j] * lattice[i + 1][j] : 0;
			E += (j + 1 != SIZE) ? lattice[i][j] * lattice[i][j + 1] : 0;
		}

	calcW();
}

void metropolis()
{
	int x, y, sum;
	for (int i = 0; i < SIZE * SIZE; i++)
	{
		x = rand() % SIZE;
		y = rand() % SIZE;
		sum = lattice[(x - 1 + SIZE) % SIZE][y] +
			lattice[(x + 1 + SIZE) % SIZE][y] +
			lattice[x][(y - 1 + SIZE) % SIZE] +
			lattice[x][(y + 1 + SIZE) % SIZE];

		if (sum * lattice[x][y] <= 0 || (rand() / (double)RAND_MAX) < w[sum / 2 + 2])
		{
			lattice[x][y] = -lattice[x][y];
			::ratio++;
			M += 2 * lattice[x][y];
			E -= 2 * lattice[x][y] * sum;
		}
	}
}

void timer1(int)
{
	display();

	metropolis();

	nmcs++;

	ecum += E;
	e2cum += E * E;
	mcum += M;
	m2cum += M * M;


	glutTimerFunc(10, timer1, 0);
}

void outputData(int)
{
	double norm = 1 / (double)(nmcs * SIZE * SIZE);

	cout << "Коэффициент принятия = " << ::ratio * norm << endl;
	cout << "Средняя энергия на спин = " << ecum * norm << endl;
	cout << "Средний квадрат энергии на спин = " << e2cum * norm << endl;
	cout << "Средняя намагниченность = " << mcum * norm << endl;
	cout << "Средний квадрат намагниченности = " << m2cum * norm << endl << endl;

	glutTimerFunc(10000, outputData, 0);
}

void keyboard(unsigned char key, int x, int y)
{
	switch (key)
	{
	case 'w': case 'W':
	{
		T += 0.01;
		T = (T >= T_MAX) ? T_MAX : T;
		calcW();
		break;
	}
	case 's': case 'S':
	{
		T -= 0.01;
		T = (T <= 0.01) ? 0.01 : T;
		calcW();
		break;
	}
	}
}

void motion(int x, int y)
{
	double k = 1 - y / (double)SIZE_PX;
	T = T_MAX * k;
	T = (T >= T_MAX) ? T_MAX : T;
	T = (T <= 0.01) ? 0.01 : T;
	calcW();
}

int main()
{
	setlocale(LC_ALL, "ru");
	init();
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowSize(SIZE_PX + 100, SIZE_PX);
	glutCreateWindow("ISING");
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0, SIZE + SIZE / 8, 0, SIZE);
	glutDisplayFunc(display);
	glutKeyboardFunc(keyboard);
	glutMotionFunc(motion);
	glutTimerFunc(1, timer1, 0);
	glutTimerFunc(10000, outputData, 0);

	glutMainLoop();
}

Отметим цель создания некоторых функций в данном программном продукте:

• init() – создание начальной конфигурации;
• display() – отрисовка решетки спинов и шкалы температуры;
• calcW() – вычисление вероятностей перехода;
• metropolis() – реализация алгоритма Метрополиса;
• timer1() – обновление данных после каждого изменения конфигурации, увеличение числа шагов Монте-Карло;
• outputData() – вычисление среднего на спин, вывод необходимых данных;
• keyboard() и motion() – возможность изменять температуру с помощью шкалы двумя путями – кнопками на клавиатуре и нажатием мыши соответственно;

Стоит сделать пару выводов:

• При критической температуре T=2,269℃ происходит фазовый переход из неупорядоченного в упорядоченное ферромагнитное состояние.
• При изменении температуры в меньшую сторону следующие физические и статистические характеристики изменяются следующим образом:
  
  • Коэффициент принятия уменьшается;
  • Средняя энергия на спин уменьшается;
  • Средний квадрат энергии на спин увеличивается;
  • Средняя намагниченность уменьшается;
  • Средний квадрат намагниченности увеличивается.

Скриншоты работы программы при понижении и повышении температуры