Содержание
- Глава 1: использование нейросетей для распознавания рукописных цифр
- Глава 2: как работает алгоритм обратного распространения
- Глава 3:
- ч.1: улучшение способа обучения нейросетей
- ч.2: почему регуляризация помогает уменьшать переобучение?
- ч.3: как выбрать гиперпараметры нейросети?
- ч.1: улучшение способа обучения нейросетей
- Глава 4: визуальное доказательство того, что нейросети способны вычислить любую функцию
- Глава 5: почему глубокие нейросети так сложно обучать?
В прошлой главе мы узнали, что глубокие нейронные сети (ГНС) часто тяжелее обучать, чем неглубокие. И это плохо, поскольку у нас есть все основания полагать, что если бы мы могли обучить ГНС, они бы гораздо лучше справлялись с задачами. Но хотя новости из предыдущей главы и разочаровывают, нас это не остановит. В этой главе мы выработаем техники, которые сможем использовать для обучения глубоких сетей и применения их на практике. Мы также посмотрим на ситуацию шире, кратко познакомимся с недавним прогрессом в использовании ГНС для распознавания изображений, речи и для других применений. А также поверхностно рассмотрим, какое будущее может ждать нейросети и ИИ.
Это будет длинная глава, поэтому давайте немного пройдёмся по оглавлению. Её разделы не сильно связаны между собой, поэтому, если у вас есть некие базовые понятия о нейросетях, вы можете начинать с того раздела, который вас больше интересует.
Основная часть главы – введение в один из наиболее популярных типов глубоких сетей: глубокие свёрточные сети (ГСС). Мы поработаем с подробным примером использования свёрточной сети, с кодом и прочим, для решения задачи классификации рукописных цифр из набора данных MNIST:

Начнём мы наш обзор свёрточных сетей с неглубоких сетей, которые мы использовали для решения этой задачи ранее в книге. В несколько этапов мы будем создавать всё более мощные сети. По пути мы будем знакомиться с многими мощными технологиями: свёртками, пулингом [pooling], использованием GPU для серьёзного увеличения объёма обучения по сравнению с тем, что делали неглубокие сети, алгоритмическим расширением обучающих данных (для уменьшения переобучения), использованием технологии исключения [dropout] (также для уменьшения переобучения), использованием ансамблей сетей, и прочим. В результате мы придём к системе, способности которой находятся почти на человеческом уровне. Из 10 000 проверочных изображений MNIST – которые система не видела во время обучения – она сумеет правильно распознать 9967. И вот некоторые из тех изображений, которые были распознаны неправильно. В правом верхнем углу указаны верные варианты; то, что показала наша программа, указано в правом нижнем углу.

Многие из них тяжело классифицировать и человеку. Возьмём, к примеру, третью цифру в верхней строке. Мне она кажется больше похожей на «9», чем на официальный вариант «8». Наша сеть тоже решила, что это «9». Подобные ошибки, по меньшей мере, вполне можно понять, а возможно, даже и одобрить. Закончим мы наше обсуждение распознавания изображений обзором потрясающего прогресса, который недавно достигли нейросети (в частности, свёрточные).
Остаток главы посвящён обсуждению глубокого обучения с более широкой и менее подробной точки зрения. Мы кратко рассмотрим другие модели НС, в частности, рекуррентные НС, и единицы долгой краткосрочной памяти, и то, как эти модели можно применять для решения задач по распознаванию речи, обработке естественного языка и других. Мы порассуждаем о будущем НС и ГО, от идей типа пользовательских интерфейсов, базирующихся на намерениях [intention-driven], до роли глубокого обучения в ИИ.
Эта глава базируется на материале предыдущих глав книги, используя и интегрируя такие идеи, как обратное распространение, регуляризация, функция softmax, и так далее. Однако для чтения этой главы не обязательно детально прорабатывать материал всех предыдущих глав. Однако не помешает прочесть главу 1, и узнать об основах НС. Когда я буду использовать концепции из глав со 2 по 5, я буду давать нужные ссылки на материал по необходимости.
Стоит отметить, чего в этой главе нет. Это не обучающий материал по последним и самым крутым библиотекам для работы с НС. Мы не собираемся обучать ГНС с десятками слоёв для решения проблем с передового края исследований. Мы будем пытаться понять некоторые основные принципы, лежащие в основе ГНС, и применять их к простому и лёгкому для понимания контексту задач MNIST. Иначе говоря, эта глава не вынесет вас на передовой рубеж области. Стремление этой и предыдущих глав – сконцентрироваться на основах, и подготовить вас к пониманию широкого спектра современных работ.
Введение в свёрточные нейросети
В предыдущих главах мы научили наши нейросети довольно неплохо распознавать изображения рукописных цифр:

Мы сделали это, используя сети, в которых соседние слои были полностью соединены друг с другом. То есть, каждый нейрон сети был связан с каждым нейроном соседнего слоя:
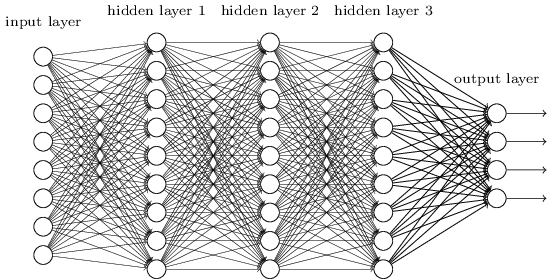
В частности, мы закодировали интенсивность каждого пикселя изображения в виде значения для соответствующего нейрона входного слоя. Для изображений размером 28х28 пикселей это означает, что у сети будет 784 (=28×28) входящих нейрона. Затем мы обучали веса и смещения сети так, чтобы на выходе сеть (была такая надежда) правильно идентифицировала входящее изображение: '0', '1', '2', ..., '8', or '9'.
Наши ранние сети работают достаточно неплохо: мы достигли точности классификации выше 98%, используя обучающие и проверочные данные из набора рукописных цифр MNIST. Но если оценить эту ситуацию теперь, то покажется странным использовать сеть с полностью связанными слоями для классификации изображений. Дело в том, что такая сеть не принимает во внимание пространственную структуру изображений. К примеру, она совершенно одинаково относится как к пикселям, расположенным далеко друг от друга, так и к соседним пикселям. Предполагается, что выводы о таких концепциях пространственной структуры должны быть сделаны на основе изучения обучающих данных. Но что, если вместо того, чтобы начинать структуру сети с чистого листа, мы будем использовать архитектуру, пытающуюся воспользоваться пространственной структурой? В данном разделе я опишу свёрточные нейронные сети (СНС). Они используют специальную архитектуру, особенно подходящую для классификации изображений. Благодаря использованию такой архитектуры, СНС обучаются быстрее. А это помогает нам обучать более глубокие и многослойные сети, которые хорошо справляются с классификацией изображений. Сегодня глубокие СНС или некий близкий к ним вариант используются в большинстве случаев распознавания изображений.
Истоки СНС уходят в 1970-е. Но стартовой работой, с которой началось их современное распространение, стал труд 1998 года "Градиентное обучение для распознавания документов". Лекун сделал интересное замечание касательно терминологии, используемой в СНС: «Связь таких моделей, как свёрточные сети, с нейробиологией весьма поверхностна. Поэтому я называю их свёрточными сетями, а не свёрточными нейросетями, и поэтому мы называем их узлы элементами, а не нейронами». Но, несмотря на это, СНС используют множество идей из мира НС, которые мы уже изучили: обратное распространение, градиентный спуск, регуляризация, нелинейные функции активации, и т.д. Поэтому мы будем следовать общепринятому соглашению и считать их разновидностью НС. Я буду называть их как сетями, так и нейросетями, а их узлы – как нейронами, так и элементами.
СНС используют три базовых идеи: локальные рецептивные поля, общие веса и пулинг. Давайте рассмотрим эти идеи по очереди.
Локальные рецептивные поля
В полносвязных слоях сетей входные слои обозначались вертикальными линиями нейронов. В СНС удобнее представлять входной слой в виде квадрата из нейронов с размерностью 28х28, значения которых соответствуют интенсивностям пикселей изображения 28х28:

Как обычно, мы связываем входящие пиксели со слоем скрытых нейронов. Однако мы не будем связывать каждый пиксель с каждым скрытым нейроном. Связи мы организуем в небольших, локализованных участках входящего изображения.
Точнее говоря, каждый нейрон первого скрытого слоя будет связан с небольшим участком входящих нейронов, к примеру, региона 5х5, соответствующего 25 входящим пикселям. Так что, для некоего скрытого нейрона связь может выглядеть так:
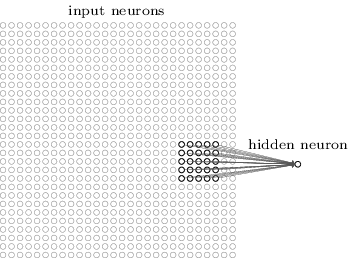
Этот участок входящего изображения называется локальным рецептивным полем для этого скрытого нейрона. Это небольшое окошко, глядящее на входящие пиксели. Каждая связь обучается своему весу. Также скрытый нейрон изучает общее смещение. Можно считать, что этот конкретный нейрон обучается анализировать своё определённое локальное рецептивное поле.
Затем мы перемещаем локальное рецептивное поле по всему входящему изображению. Для каждого локального рецептивного поля существует свой скрытый нейрон в первом скрытом слое. Для более конкретной иллюстрации начнём с локального рецептивного поля в левом верхнем углу:

Сдвинем локальное рецептивное поле на один пиксель вправо (на один нейрон), чтобы связать его со вторым скрытым нейроном:

Таким образом, мы построим первый скрытый слой. Отметьте, что если наше входящее изображение имеет размеры 28х28, а размеры локального рецептивного поля составляют 5х5, тогда в скрытом слое будет 24х24 нейрона. Это оттого, что мы можем сдвинуть локальное рецептивное поле только на 23 нейрона вправо (или вниз), а потом столкнёмся с правой (или нижней) стороной входящего изображения.
В данном примере локальные рецептивные поля двигаются по одному пикселю за раз. Но иногда используется другой размер шага. К примеру, мы могли бы сдвигать локальное рецептивное поле на 2 пикселя в сторону, и в этом случае можно говорить о размере шага 2. В данной главе мы в основном будем использовать шаг 1, но стоит знать, что иногда проходят эксперименты с шагами другого размера. С размером шага можно поэкспериментировать, как и с другими гиперпараметрами. Можно также изменять и размер локального рецептивного поля, однако обычно оказывается, что больший размер локального рецептивного поля лучше работает на изображениях, значительно больших, чем 28х28 пикселей.
Общие веса и смещения
Я упомянул, что у каждого скрытого нейрона есть смещение и 5х5 весов, связанных с его локальным рецептивным полем. Но я не упомянул, что мы будем использовать одинаковые веса и смещения для всех 24х24 скрытых нейронов. Иначе говоря, для скрытого нейрона j,k выход будет равен:
Здесь σ — функция активации, возможно, сигмоида из прошлых глав. b – общее значение смещения. wl,m — массив общих весов 5х5. И, наконец, ax,y обозначает входную активацию в позиции x,y.
Это значит, что все нейроны в первом скрытом слое обнаруживают один и тот же признак, просто находящийся в разных частях изображения. Признак, обнаруживаемый скрытым нейроном – это некая входящая последовательность, приводящая к активации нейрона: возможно, край изображения, или некая форма. Чтобы понять, почему это имеет смысл, допустим, что наши веса и смещение таковы, что скрытый нейрон может распознать, предположим, вертикальную грань в определённом локальном рецептивном поле. Эта способность, вероятно, окажется полезной и в других местах изображения. Поэтому полезно применять один и тот же детектор признаков по всей площади изображения. Говоря более абстрактно, СНС хорошо приспособлены к трансляционной инвариантности изображений: передвиньте изображение, к примеру, кота, немного в сторону, и оно всё равно останется изображением кота. Правда, изображения из задачи классификации цифр MNIST все отцентрованы и нормализованы по размеру. Поэтому у MNIST меньше трансляционной инвариантности, чем у случайных картинок. И всё же, такие признаки, как грани и углы, вероятно, окажутся полезными по всей поверхности входящего изображения.
По этой причине иногда мы называем сопоставление входящего слоя и скрытого слоя картой признаков. Веса, определяющие карту признаков, мы называем общими весами. А смещение, определяющее карту признаков – общим смещением. Часто говорят, что общие веса и смещение определяют ядро [kernel] или фильтр. Но в литературе люди иногда используют эти термины немного по другому поводу, и поэтому я не буду сильно углубляться в терминологию; лучше давайте посмотрим на несколько конкретных примеров.
Описанная мною структура сети способна распознать только локализованный признак одного вида. Чтобы распознавать изображения, нам понадобится больше карт признаков. Поэтому законченный свёрточный слой состоит из нескольких различных карт признаков:
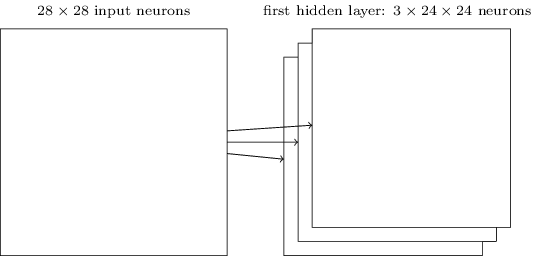
В примере показано 3 карты признаков. Каждая карта определяется набором из общих весов 5х5 и одним общим смещением. В итоге такая сеть может распознать три разных типа признаков, и каждый признак она сможет найти в любой части изображения.
Три карты признаков я нарисовал для простоты. На практике же СНС могут использовать больше (возможно, гораздо больше) карт признаков. Одна из ранних СНС, LeNet-5, использовала 6 карт признаков, каждая из которых была связана с рецептивным полем 5х5, для распознавания цифр MNIST. Поэтому приведённый выше пример очень похож на LeNet-5. В примерах, которые мы будем самостоятельно разрабатывать далее, мы будем использовать свёрточные слои, содержащие по 20 и 40 карт признаков. Давайте быстренько посмотрим на те признаки, что мы изучим:

Эти 20 изображений соответствуют 20 различным картам признаков (фильтрам, или ядрам). Каждая карта представляется изображением 5х5, соответствующим 5х5 весам локального рецептивного поля. Белые пиксели означают малый (обычно, более отрицательный) вес, и на соответствующие им пиксели карта признаков реагирует меньше. Тёмные пиксели означают больший вес, и на соответствующие им пиксели карта признаков реагирует больше. Очень грубо говоря, эти изображения демонстрируют те признаки, на которые реагирует свёрточный слой.
Какие выводы можно сделать на основе этих карт признаков? Пространственные структуры здесь, очевидно, появились не случайным образом – у многих признаков видно явные светлые и тёмные участки. Это говорит о том, что наша сеть действительно обучается чему-то, связанному с пространственными структурами. Однако кроме этого достаточно сложно понять, что это за признаки. Мы явно не изучаем, допустим, фильтры Габора, которые использовались во многих традиционных подходах к распознаванию образов. На самом деле сейчас проводится большая работа, связанная с тем, чтобы лучше понять, какие именно признаки изучают СНС. Если вам это интересно, рекомендую начать с работы 2013 года.
Большое преимущество общих весов и смещений состоит в том, что это кардинально уменьшает количество параметров, имеющихся у СНС. Для каждой карты признаков нам понадобится 5×5=25 общих весов и одно общее смещение. Поэтому для каждой карты признаков требуется 26 параметров. Если у нас имеется 20 карт признаков, то всего у нас будет 20×26=520 параметров, определяющих свёрточный слой. Для сравнения, предположим, что у нас есть полносвязный первый слой с 28×28=784 входящими нейронами и относительно скромные 30 скрытых нейронов – такую схему мы использовали ранее во множестве примеров. Получается 784×30 весов, плюс 30 смещений, итого 23 550 параметров. Иначе говоря, у полносвязного слоя будет более чем 40 раз больше параметров, чем у свёрточного.
Конечно, мы не можем напрямую сравнивать количество параметров, поскольку эти две модели различаются кардинальным образом. Но интуитивно кажется, что использование трансляционной инвариантности свёрточным слоем уменьшает количество параметров, необходимых для достижения эффективности, сравнимой с таковой у полносвязной модели. А это, в свою очередь, приведёт к ускорению обучения свёрточной модели, и в итоге поможет нам создать более глубокие сети при помощи свёрточных слоёв.
Кстати, название «свёрточные» происходит от операции в уравнении (125), которую иногда называют свёрткой. Точнее, иногда люди записывают это уравнение, как a1=σ(b+w∗a0), где a1 обозначает набор выходных активаций одной карты признаков, a0 — набор входных активаций, а * называется операцией свёртки. Мы не будем глубоко зарываться в математику свёрток, поэтому вам не нужно особенно беспокоиться по поводу этой связи. Но просто стоит знать, откуда взялось название.
Пулинговые слои
Кроме описанных свёрточных слоёв в СНС есть ещё и пулинговые слои. Они обычно используются сразу после свёрточных. Они занимаются тем, что упрощают информацию с выхода свёрточного слоя.
Здесь я использую фразу «карта признаков» не в значении функции, вычисляемой свёрточным слоем, а для обозначения активации выхода скрытых нейронов слоя. Такое вольное использование терминов часто встречается в исследовательской литературе.
Пулинговый слой принимает выход каждой карты признаков свёрточного слоя и готовит сжатую карту признаков. К примеру, каждый элемент пулингового слоя может просуммировать участок из, допустим, 2х2 нейронов предыдущего слоя. Конкретный пример: одна распространённая процедура пулинга известна, как макс-пулинг. В макс-пулинге элемент пулинга просто выдаёт максимальную активацию из участка 2х2, как показано на диаграмме:

Поскольку выход нейронов свёрточного слоя даёт 24х24 значения, после пулинга мы получим 12х12 нейронов.
Как упомянуто выше, свёрточный слой обычно подразумевает нечто большее, чем единственная карта признаков. Мы применяем макс-пулинг к каждой карте признаков по отдельности. Так что, если у нас есть три карты признаков, комбинированные свёрточные и макс-пулинговые слои будут выглядеть так:
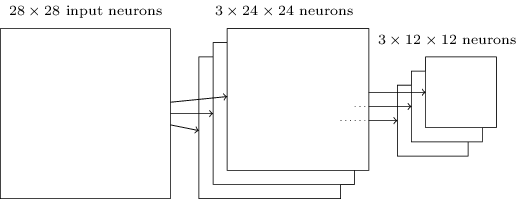
Макс-пулинг можно представить себе, как способ сети спросить, есть ли данный признак в каком-либо месте изображения. А затем она отбрасывает информацию о его точном расположении. Интуитивно понятно, что когда признак найден, то его точное расположение уже не так важно, как его примерное расположение относительно других признаков. Преимущество состоит в том, что количество признаков, полученных при помощи пулинга, оказывается гораздо меньшим, и это помогает уменьшить количество параметров, требуемых в следующих слоях.
Макс-пулинг – не единственная технология пулинга. Ещё один распространённый подход известен, как L2-пулинг. В нём вместо того, чтобы взять максимальную активацию региона нейронов 2х2, мы берём квадратный корень из суммы квадратов активаций региона 2х2. Детали подходов отличаются, но интуитивно он похож на макс-пулинг: L2-пулинг – это способ сжатия информации со свёрточного слоя. На практике часто используются обе технологии. Иногда люди используют другие типы пулинга. Если вы изо всех сил стараетесь оптимизировать качество работы сети, вы можете использовать подтверждающие данные для сравнения нескольких разных подходов к пулингу, и выбрать наилучший. Но мы не будем беспокоиться насчёт настолько подробной оптимизации.
Суммируя
Теперь мы можем свести всю информацию вместе и получить полноценную СНС. Она похожа на недавно рассмотренную нами архитектуру, однако у неё есть дополнительный слой из 10 выходных нейронов, соответствующих 10 возможным значениям цифр MNIST ('0', '1', '2',..):
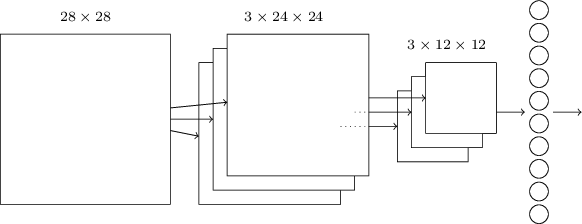
Сеть начинает с 28х28 входных нейронов, используемых для кодирования интенсивности пикселей изображения MNIST. После этого идёт свёрточный слой, использующий локальные рецептивные поля 5х5 и 3 карты признаков. В итоге получается слой из 3х24х24 скрытых нейронов признаков. Следующий шаг – слой макс-пулинга, применяемый к участкам 2х2, на каждой из трёх карт признаков. В итоге получается слой из 3х12х12 скрытых нейронов признаков.
Последний слой связей в сети полносвязный. То есть, он связывает каждый нейрон слоя макс-пулинга с каждым из 10 выходных нейронов. Такую полносвязную архитектуру мы использовали ранее. Обратите внимание, что на диаграмме выше я для простоты использовал одну стрелочку, не показывая всех связей. Вы легко можете представить себе их все.
Такая свёрточная архитектура сильно отличается от тех, что мы использовали ранее. Однако общая картина схожа: сеть, состоящая из множества простых элементов, чьё поведение определяется весами и смещениями. Цель остаётся той же: использовать обучающие данные для обучения сети весам и смещениям, чтобы сеть хорошо классифицировала входящие цифры.
В частности, как и в предыдущих главах, мы будем обучать нашу сеть при помощи стохастического градиентного спуска и обратного распространения. Процедура идёт практически так же, как и раньше. Однако нам нужно внести несколько изменений в процедуру обратного распространения. Дело в том, что наши производные для обратного распространения предназначались для сети с полностью связанными слоями. К счастью, изменить производные для свёрточных и макс-пулинговых слоёв весьма просто. Если вам хочется разобраться в деталях, приглашаю вас попробовать решить следующую задачу. Предупрежу, что на неё уйдёт достаточно много времени, если только вы не разобрались досконально в ранних вопросах дифференцирования обратного распространения.
Задача
- Обратное распространение в свёрточной сети. Главными уравнениями обратного распространения в сети с полностью связанными слоями будут (BP1)-(BP4). Допустим, наша сеть содержит свёрточный слой, слой макс-пулинга и полностью связанный выходной слой, как в описанной выше сети. Как нужно изменить уравнения обратного распространения?
Свёрточные нейронные сети на практике
Мы обсудили идеи, лежащие в основе СНС. Давайте посмотрим, как они работают на практике, реализовав некоторые СНС, и применив их к задаче классификации цифр MNIST. Мы будем использовать программу network3.py, улучшенную версию программ network.py и network2.py, созданных в предыдущих главах. Программа network3.py использует идеи из документации библиотеки Theano (в частности, реализацию LeNet-5), из реализации исключения от Миша Денила и Криса Олаха. Код программы доступен на GitHub. В следующем разделе мы изучим код программы network3.py, а в данном разделе мы используем её, как библиотеку для создания СНС.
Программы network.py и network2.py были написаны на python с использованием матричной библиотеки Numpy. Они работали на основе первых принципов, и доходили до самых подробных деталей обратного распространения, стохастического градиентного спуска, и т.д. Но теперь, когда мы разбираемся в этих деталях, для network3.py мы будем использовать библиотеку машинного обучения Theano (см. научную работу с её описанием). Также Theano лежит в основе популярных библиотек для НС Pylearn2 и Keras, а также Caffe и Torch.
Использование Theano облегчает реализацию обратного распространения в СНС, поскольку автоматически подсчитывает все карты. Также Theano заметно выигрывает по скорости у нашего предыдущего кода (который был написан для облегчения понимания, а не для скоростной работы), поэтому её разумно использовать для обучения более сложных сетей. В частности, одной из великолепных возможностей Theano является запуск кода как на CPU, так и на GPU, при наличии. Запуск на GPU даёт значительный прирост в скорости, и помогает обучать более сложные сети.
Чтобы работать параллельно с книгой, вам нужно установить Theano на своей системе. Для этого следуйте инструкциям на домашней странице проекта. На момент написания книги и запуска примеров существовала версия Theano 0.7. Некоторые эксперименты я запускал на Mac OS X Yosemite без GPU. Некоторые на Ubuntu 14.04 с NVIDIA GPU. А некоторые – и там, и там. Чтоб запустить network3.py, установите в коде флажок GPU в значение True или False. Кроме этого, для запуска Theano на GPU вам могут помочь следующие инструкции. Также в сети легко найти обучающие материалы. Если у вас нет своего GPU, можете посмотреть в сторону Amazon Web Services EC2 G2. Но даже при наличии GPU наш код будет работать не очень быстро. Многие эксперименты будут идти от нескольких минут до нескольких часов. Самые сложные из них на одном только CPU будут выполняться по нескольку дней. Как и в предыдущих главах, рекомендую запускать эксперимент, и продолжать чтение, периодически проверяя его работу. Без использования GPU рекомендую вам уменьшить количество эпох обучения для самых сложных экспериментов.
Чтобы получить базовые результаты для сравнения, начнём с неглубокой архитектуры с одним скрытым слоем, содержащим 100 скрытых нейронов. Мы будем обучаться 60 эпох, использовать скорость обучения η=0,1, размер мини-пакета 10, и будем учиться без регуляризации.
В данном разделе я задаю конкретное количество эпох обучения. Я делаю это для ясности в процессе обучения. На практике полезно использовать ранние остановки, отслеживая точность подтверждающего набора, и останавливать обучение, когда мы убеждаемся в том, что точность подтверждения перестаёт улучшаться:
>>> import network3
>>> from network3 import Network
>>> from network3 import ConvPoolLayer, FullyConnectedLayer, SoftmaxLayer
>>> training_data, validation_data, test_data = network3.load_data_shared()
>>> mini_batch_size = 10
>>> net = Network([
FullyConnectedLayer(n_in=784, n_out=100),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(training_data, 60, mini_batch_size, 0.1,
validation_data, test_data)Наилучшая точность классификации составила 97,80%. Это точность классификации test_data, оценённая по обучающей эпохе, в которой мы получили наилучшую точность классификации данных из validation_data. Использование подтверждающих данных для принятия решения об оценке точности помогает избежать переобучения. Далее мы так и будем поступать. Ваши результаты могут немного отличаться, поскольку веса и смещения сети инициализируются случайным образом.
Точность в 97,80% довольно близка к точности в 98,04%, полученной в главе 3, с использованием сходной архитектуры сети и гиперпараметров обучения. В частности, в обоих примерах используются неглубокие сети с одним скрытым слоем, содержащим 100 скрытых нейронов. Обе сети обучаются 60 эпох с размером мини-пакета 10 и скоростью обучения η=0,1.
Однако в более ранней сети имелись два отличия. Во-первых, мы проводили регуляризацию, чтобы помочь уменьшить влияние переобучения. Регуляризация текущей сети улучшает точность, но очень ненамного, поэтому мы пока не будем думать об этом. Во-вторых, хотя последний слой ранней сети использовал сигмоидные активации и функцию стоимости с перекрёстной энтропией, текущая сеть использует последний слой с softmax, и логарифмическую функцию правдоподобия в качестве функции стоимости. Как описано в главе 3, это не крупное изменение. Я перешёл с одного на другое не по какой-то глубокой причине – в основном потому, что softmax и логарифмическая функция правдоподобия чаще используется в современных сетях для классификации изображений.
Можем ли мы улучшить результаты, используя более глубокую архитектуру сети?
Начнём со вставки свёрточного слоя, в самом начале сети. Мы будем использовать локальное рецептивное поле 5х5, шаг длиной 1 и 20 карт признаков. Мы также вставим слой макс-пулинга, комбинирующий признаки при помощи окон пулинга 2х2. Так что общая архитектура сети будет выглядеть похоже на ту, что мы обсуждали в предыдущем разделе, но с дополнительным полносвязным слоем:
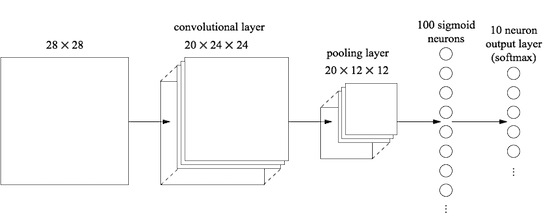
В этой архитектуре свёрточный и пулинговый слой обучаются локальной пространственной структуре, содержащейся во входящей обучающей картинке, а последний, полносвязный слой обучается уже на более абстрактном уровне, интегрируя глобальную информацию со всего изображения. Это часто применяющаяся схема в СНС.
Давайте обучим такую сеть, и посмотрим, как она себя поведёт.
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2)),
FullyConnectedLayer(n_in=20*12*12, n_out=100),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(training_data, 60, mini_batch_size, 0.1,
validation_data, test_data) Мы получаем точность в 98,78%, что значительно выше любого из предыдущих результатов. Мы уменьшили ошибку больше, чем на треть – великолепный результат.
Описывая структуру сети, я считал свёрточные и пулинговые слои единым слоем. Рассматривать их, как отдельные слои, или как единый слой – вопрос предпочтений. network3.py считает их одним слоем, поскольку так код получается компактнее. Однако легко изменить network3.py так, чтобы слои можно было задавать по отдельности.
Упражнение
- Какую точность классификации мы получим, если опустим полносвязный слой, и будем использовать только свёрточный/пулинговый слой и слой softmax? Помогает ли включение полносвязного слоя?
Можем ли мы улучшить результат в 98,78%?
Попробуем вставить второй свёрточный/пулинговый слой. Мы вставим его между существующим свёрточным/пулинговым и полносвязным скрытым слоями. Мы снова используем локальное рецептивное поле 5х5 и пул по участкам 2х2. Посмотрим, что случится, когда мы обучим сеть с примерно такими же гиперпараметрами, что и ранее:
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2)),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2)),
FullyConnectedLayer(n_in=40*4*4, n_out=100),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(training_data, 60, mini_batch_size, 0.1,
validation_data, test_data) И вновь у нас улучшение: теперь мы получаем точность в 99,06%!
На текущий момент возникает два естественных вопроса. Первый: а что вообще означает применение второго свёрточного/пулингового слоя? Вы можете считать, что у второго свёрточного/пулингового слоя на вход приходят «изображения» размером 12х12, чьи «пиксели» представляют наличие (или отсутствие) определенных локализованных признаков в изначальной входящей картинке. То есть, можно считать, что на вход этому слою приходит некий вариант изначальной входящей картинки. Это будет более абстрактная и сжатая версия, но у неё всё равно есть достаточно пространственной структуры, поэтому имеет смысл использовать для её обработки второй свёрточно/пулинговый слой.
Приятная точка зрения, но она порождает второй вопрос. На выходе с предыдущего слоя получается 20 отдельных КП, поэтому на второй свёрточно/пулинговый слой приходит 20х12х12 групп входных данных. Получается, что у нас есть как бы 20 отдельных изображений, входящих на свёрточно/пулинговый слой, а не одно изображение, как это было в случае с первым свёрточно/пулинговым слоем. Как же нейроны из второго свёрточно/пулингового слоя должны реагировать на множество этих входящих изображений? На самом деле мы просто позволим каждому нейрону этого слоя обучаться на основе всех 20х5х5 входящих в его локальное рецептивное поле нейронов. Говоря менее формальным языком, у детекторов признаков во втором свёрточно/пулинговом слое будет доступ ко всем признакам первого слоя, но только в рамках их конкретных локальных рецептивных полей.
Кстати, такая проблема возникла бы и у первого слоя, если бы изображения были цветными. В данном случае у нас было бы 3 входных признака на каждый пиксель, соответствующих красному, зелёному и синему каналам оригинальной картинки. И мы бы тогда тоже дали детекторам признаков доступ ко всей цветовой информации, но только в рамках их локального рецептивного поля.
Задача
- Использование функции активации в виде гиперболического тангенса. Ранее в этой книге я уже несколько раз упоминал свидетельства в пользу того, что функция tanh, гиперболический тангенс, может лучше подойти на роль функции активации, чем сигмоида. Мы ничего с этим не делали, поскольку у нас и с сигмоидой был хороший прогресс. Но давайте попробуем провести несколько экспериментов с tanh в качестве функции активации. Попробуйте обучить сеть с танг-активацией со свёрточными и полносвязными слоями (вы можете передать activation_fn=tanh как параметр классам ConvPoolLayer и FullyConnectedLayer). Начните с тех же гиперпараметров, что были у сигмоидной сети, но обучайте сеть 20 эпох, а не 60. Как ведёт себя сеть? Что будет, если продолжить до 60-й эпохи? Попробуйте построить график точности подтверждения работы по эпохам для тангенса и сигмоиды, вплоть до 60-й эпохи. Если ваши результаты будут похожими на мои, вы обнаружите, что сеть на основе тангенса обучается чуть быстрее, но итоговая точность обеих сетей одинаковая. Можете объяснить, почему так происходит? Можно ли достичь той же скорости обучения при помощи сигмоиды – например, изменив скорость обучения или через масштабирование (вспомните, что σ(z)=(1+tanh(z/2))/2)? Попробуйте пять-шесть разных гиперпараметров или архитектур сети, поищите, где тангенс может опережать сигмоиду. Отмечу, что эта задача открытая. Лично я не нашёл каких-то серьёзных преимуществ в переходе на тангенс, хотя я не проводил всеобъемлющих экспериментов, и, возможно, вы их найдёте. В любом случае, скоро мы найдём преимущество в переходе на выпрямленную линейную функцию активации, поэтому больше не будем углубляться в вопрос с гиперболическим тангенсом.
Использование выпрямленных линейных элементов
Разработанная нами на текущий момент сеть является одним из вариантов сетей, использованных в плодотворной работе 1998 года, в которой была впервые представлена задача MNIST – сети под названием LeNet-5. Это хорошая основа для дальнейших экспериментов, для улучшения понимания вопроса и интуиции. В частности, существует множество способов, которыми мы можем изменять нашу сеть в поисках способов улучшения результатов.
Вначале давайте поменяем наши нейроны так, чтобы вместо использования сигмоидной функции активации мы могли использовать выпрямленные линейные элементы (ReLU). То есть, мы будем использовать функцию активации вида f(z) ≡ max(0,z). Мы будем обучать сеть 60 эпох, со скоростью η=0,03. Я также обнаружил, что немного удобнее использовать регуляризацию L2 с параметром регуляризации λ=0.1:
>>> from network3 import ReLU
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(training_data, 60, mini_batch_size, 0.03,
validation_data, test_data, lmbda=0.1)Я получил точность классификации в 99,23%. Скромное улучшение по сравнению с результатами сигмоиды (99,06%). Однако во всех моих экспериментах я обнаруживал, что сети, основанные на ReLU, с завидным постоянством опережали сети, основанные на сигмоидной функции активации. Судя по всему, в переходе на ReLU для решения данной задачи существуют реальные преимущества.
Из-за чего функция активации ReLU работает лучше, чем сигмоида или гиперболический тангенс? В настоящий момент мы не особенно хорошо понимаем это. Обычно говорят о том, что функция max(0,z) не насыщается при больших z, в отличие от сигмоидных нейронов, и это помогает ReLU-нейронам продолжать обучение. Не спорю, но такое оправдание нельзя назвать всеобъемлющим, это просто некое наблюдение (напомню, что насыщение мы обсуждали в главе 2).
ReLU начали активно использовать в последние несколько лет. Их взяли на вооружение по эмпирическим причинам: некоторые люди попробовали ReLU, часто просто на основании предчувствий или эвристических аргументов. Они получили хорошие результаты, и практика распространилась. В идеальном мире у нас была бы теория, говорящая нам о том, для каких приложений какие функции активации подойдут лучше. Но пока что нам ещё предстоит долгий путь до такой ситуации. Я вовсе не удивлюсь, если дальнейшие улучшения работы сетей можно будет получить, выбрав какую-нибудь ещё более подходящую функцию активации. Также я ожидаю, что в ближайшие десятилетия будет выработана хорошая теория функций активации. Но сегодня нам приходится полагаться на плохо изученные эмпирические правила и опыт.
Расширение обучающих данных
Ещё один способ, который, возможно, может помочь нам улучшить результаты – это алгоритмически расширить обучающие данные. Простейший способ расширения обучающих данных – сдвиг каждой обучающей картинки на один пиксель, вверх, вниз, вправо или влево. Это можно сделать, запустив программу expand_mnist.py.
$ python expand_mnist.pyЗапуск программы превращает 50 000 обучающих изображений MNIST в расширенный набор из 250 000 обучающих изображений. Затем мы можем использовать эти обучающие изображения для обучения сети. Мы будем использовать ту же сеть, что и ранее, с ReLU. В моих первых экспериментах я уменьшал количество эпох обучения – это имело смысл, ведь у нас есть в 5 раз больше обучающих данных. Однако расширение набора данных значительно уменьшило эффект переобучения. Поэтому, проведя несколько экспериментов, я вернулся к количеству эпох 60. В любом случае, давайте обучать:
>>> expanded_training_data, _, _ = network3.load_data_shared(
"../data/mnist_expanded.pkl.gz")
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03,
validation_data, test_data, lmbda=0.1)Используя расширенные обучающие данные, я получил точность в 99.37%. Такое почти тривиальное изменение даёт значительное улучшение в точности классификации. И, как мы обсуждали ранее, алгоритмическое расширение данных можно развивать и далее. Просто, чтобы напомнить вам: в 2003 году Симард, Штейнкраус и Платт улучшили точность работы своей сети до 99,6%. Их сеть была похожа на нашу, они использовали два свёрточно/пулинговых слоя, за которым следовал полносвязный слой со 100 нейронами. Детали их архитектуры различались – у них не было возможности использовать преимущество ReLU, к примеру – однако ключом к улучшению качества работы было расширение обучающих данных. Они достигли этого поворотом, переносом и искажением обучающих изображений MNIST. Также они разработали процесс «эластичного искажения», эмулируя случайные колебания мускулов руки при письме. Скомбинировав все эти процессы, они значительно увеличили эффективный объём их базы обучающих данных, и за счёт этого достигли точности в 99,6%.
Задача
- Идея свёрточных слоёв состоит в том, чтобы работать вне зависимости от местоположения на изображении. Но тогда может показаться странным, что наша сеть лучше обучается, когда мы просто сдвигаем входные изображения. Можете ли вы объяснить, почему на самом деле это вполне разумно?
Добавление дополнительного полносвязного слоя
А можно ли ещё улучшить ситуацию? Одна из возможностей – использовать точно такую же процедуру, однако при этом увеличить размер полносвязного слоя. Я запускал программу с 300 и с 1000 нейронов, и получал результаты в 99,46% and 99,43% соответственно. Это интересно, но не особенно убедительно превосходит предыдущий результат (99,37%).
Что насчёт добавления дополнительного полносвязного слоя? Давайте попробуем добавить дополнительный полносвязный слой, чтобы у нас было два скрытых полносвязных слоя по 100 нейронов:
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU),
FullyConnectedLayer(n_in=100, n_out=100, activation_fn=ReLU),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03,
validation_data, test_data, lmbda=0.1)Таким образом я достиг точности проверки в 99,43%. Расширенная сеть снова не сильно улучшила показатели. Проведя похожие эксперименты с полносвязными слоями на 300 и 100 нейронов, я получил точность в 99,48% и 99,47%. Вдохновляющее, но не похоже на реальный выигрыш.
Что происходит? Неужели расширенные или дополнительные полносвязные слои не помогают в решении задачи MNIST? Или же наша сеть может достичь лучшего, но мы развиваем её не в ту сторону? Может быть, мы могли, например, использовать более жёсткую регуляризацию для уменьшения переобучения. Одна из возможностей – техника исключения [dropout], упомянутая в главе 3. Вспомним, что базовая идея исключения – удалить случайным образом отдельные активации при обучении сети. В итоге модель становится более устойчивой к потере отдельных свидетельств, и поэтому менее вероятно, что она будет полагаться на какие-то мелкие нестандартные особенности обучающих данных. Давайте попробуем применить исключение к последнему полносвязному слою:
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
FullyConnectedLayer(
n_in=40*4*4, n_out=1000, activation_fn=ReLU, p_dropout=0.5),
FullyConnectedLayer(
n_in=1000, n_out=1000, activation_fn=ReLU, p_dropout=0.5),
SoftmaxLayer(n_in=1000, n_out=10, p_dropout=0.5)],
mini_batch_size)
>>> net.SGD(expanded_training_data, 40, mini_batch_size, 0.03,
validation_data, test_data)Используя такой подход, мы достигаем точности в 99,60%, что значительно лучше предыдущих, особенно нашей базовой оценки – сети со 100 скрытыми нейронами, дающей точность в 99,37%.
Тут стоит отметить два изменения.
Во-первых, я уменьшил количество эпох обучения до 40: исключение уменьшает переобучение, и мы учимся быстрее.
Во-вторых, в полносвязных скрытых слоях содержится 1000 нейронов, а не 100, как раньше. Конечно, исключение, по сути, устраняет многие нейроны во время обучения, поэтому стоит ожидать некоего расширения. На самом деле, я проводил эксперименты с 300 и 1000 нейронов, и получил чуть более качественное подтверждение в случае с 1000 нейронов.
Использование ансамбля сетей
Лёгкий способ улучшить эффективность – создать несколько нейросетей, а потом заставить их голосовать за лучшую классификацию. Допустим, к примеру, что мы обучили 5 разных НС с использованием вышеуказанного рецепта, и каждая из них достигла точности, близкой к 99,6%. И хотя все сети покажут сходную точность, у них могут быть разные ошибки из-за разной случайной инициализации. Разумно предположить, что если 5 НС проголосуют, их общая классификация будет лучше, чем у любой сети в отдельности.
Звучит слишком хорошо, чтобы быть правдой, но сборка подобных ансамблей – распространённый трюк как для НС, так и для других техник МО. И он на самом деле даёт улучшение эффективности: мы получаем точность в 99,67%. Иначе говоря, наш ансамбль сетей правильно классифицирует все 10 000 проверочных изображений, за исключением 33.
Оставшиеся ошибки показаны ниже. Метка в правом верхнем углу – правильная классификация согласно данным MNIST, а в правом нижнем – метка, полученная ансамблем сетей:

Стоит подробнее остановиться на изображениях. Первые две цифры, 6 и 5 – реальные ошибки нашего ансамбля. Однако их можно понять, такую ошибку мог сделать и человек. Эта 6 реально очень похожа на 0, а 5 очень похожа на 3. Третья картинка, якобы 8, действительно больше похожа на 9. Я встаю на сторону ансамбля сетей: думаю, что он справился с работой лучше, чем человек, написавший эту цифру. С другой стороны, четвёртое изображение, 6, реально неправильно классифицирована сетями.
И так далее. В большинстве случаев решение сети выглядит правдоподобным, а в некоторых случаях они лучше классифицировали цифру, чем человек её написал. В целом наши сети демонстрируют исключительную эффективность, особенно если вспомнить, что они правильно классифицировали 9967 изображений, которые мы здесь не приводим. В таком контексте несколько явных ошибок можно понять. Даже осторожный человек иногда ошибается. Поэтому я могу ожидать лучшего результата только от чрезвычайно аккуратного и методичного человека. Наша сеть приближается к эффективности человека.
Почему мы применили исключение только к полносвязным слоям
Если внимательно посмотреть на приведённый выше код, вы увидите, что исключение мы применили только к полносвязным слоям сети, но не к свёрточным. В принципе можно применить схожую процедуру и к свёрточным слоям. Но в этом нет нужды: у свёрточных слоёв есть значительное встроенное сопротивление к переобучению. Всё потому, что общие веса заставляют свёрточные фильтры обучаться по всей картинке сразу. В итоге они с меньшей вероятностью споткнуться о какие-то локальные искажения в обучающих данных. Поэтому нет особой нужды применять к ним другие регуляризаторы, типа исключения.
Двигаемся дальше
Можно улучшить эффективность решения задачи MNIST ещё больше. Родриго Бененсон собрал информативную табличку, где показан прогресс сквозь года, и приведены ссылки на работы. Многие из работ используют ГСС примерно так же, как их использовали мы. Если вы пороетесь в работах, вы найдёте много интересных техник, и вам может понравиться реализовывать какие-то из них. В таком случае разумно будет начать их реализацию с простой сети, которую можно быстро обучать, и это поможет вам быстрее начать понимать происходящее.
По большей части я не буду пытаться обозревать недавние работы. Но не могу удержаться от одного исключения. Речь идёт об одной работе 2010 года. Мне нравится в ней её простота. Сеть – многослойная, и использует только полносвязные слои (без свёрток). В наиболее успешной их сети есть скрытые слои, содержащие 2500, 2000, 1500, 1000 и 500 нейронов соответственно. Они использовали схожие идеи для расширения обучающих данных. Но кроме этого, они применили ещё несколько трюков, включая отсутствие свёрточных слоёв: это была простейшая, ванильная сеть, которую при должном терпении и наличии подходящих компьютерных мощностей могли обучить ещё в 1980-х (если бы тогда существовал набор MNIST). Они достигли точности классификации в 99,65%, что примерно совпадает с нашей. Главное в их работе – использование очень крупной и глубокой сети, и использование GPU для ускорения обучения. Это позволило им обучаться множество эпох. Они также воспользовались большой длиной промежутков обучения, и постепенно уменьшали скорость обучения с 10-3 до 10-6. Пытаться достичь подобных результатов с такой архитектурой, как у них – интересное упражнение.
Почему у нас получается обучаться?
В предыдущей главе мы увидели фундаментальные препятствия обучению глубоких многослойных НС. В частности, мы видели, что градиент становится очень нестабильным: при продвижении от выходного слоя к предыдущим градиент склонен либо к исчезновению (проблема исчезающего градиента) или к взрывному росту (проблема взрывного роста градиента). Поскольку градиент – это сигнал, используемый нами для обучения, это порождает проблемы.
Как нам удалось их избежать?
Ответ, естественно, такой: нам не удалось их избежать. Вместо этого мы сделали несколько вещей, позволившие нам продолжать работу, несмотря на это. В частности: (1) использование свёрточных слоёв сильно уменьшает количество содержащихся в них параметров, сильно облегчая проблему обучения; (2) использование более эффективных техник регуляризации (исключения и свёрточных слоёв); (3) использование ReLU вместо сигмоидных нейронов для ускорения обучения – эмпирически до 3-5 раз; (4) использование GPU и возможность обучаться в течение долгого времени. В частности, в последних экспериментах мы обучались 40 эпох, используя набор данных, в 5 раз больший, чем стандартные обучающие данные MNIST. Ранее в книге мы в основном обучались 30 эпох, используя стандартные обучающие данные. Комбинация факторов (3) и (4) даёт такой эффект, будто бы мы обучались в 30 раз дольше, чем ранее.
Вы, наверное, скажете «И это всё? Это всё, что нужно для обучения глубоких нейросетей? А из-за чего тогда сыр-бор загорелся?»
Мы, конечно, использовали и другие идеи: достаточно большие наборы данных (чтобы помочь избежать переобучения); правильная функция стоимости (чтобы избежать замедления обучения); хорошая инициализация весов (также во избежание замедления обучения из-за насыщения нейронов); алгоритмическое расширение набора обучающих данных. Мы обсудили эти и другие идеи в предыдущих главах, и обычно у нас была возможность повторно использовать их с небольшими примечаниями и в этой главе.
По всему видно, что это довольно простой набор идей. Простой, однако, способный на многое при использовании в комплексе. Оказалось, что начать работу с глубоким обучением было довольно легко!
Ну а насколько же глубоки эти сети?
Если считать свёрточно/пулинговые слои за один, то в нашей итоговой архитектуре есть 4 скрытых слоя. Заслуживает ли такая сеть звания глубокой? Естественно, ведь 4 скрытых слоя – это куда как больше, чем в неглубоких сетях, изучавшихся нами ранее. У большей части сетей было по одному скрытому слою, иногда – 2. С другой стороны, в современных передовых сетях иногда есть десятки скрытых слоёв. Иногда я встречал людей, считавших, что чем глубже сеть, тем лучше, и что если вы не используете достаточно большое количество скрытых слоёв, значит, на самом деле вы не занимаетесь глубоким обучением. Я так не считаю, в частности потому, что такой подход превращает определение глубокого обучения в процедуру, зависящую от сиюминутных результатов. Реальным прорывом в этой области была идея о практичности выхода за пределы сетей с одним-двумя скрытыми слоями, преобладавших в середине 2000-х. Это был реальный прорыв, открывший область исследований с более выразительными моделями. Ну а конкретное количество слоёв не представляет фундаментального интереса. Использование глубоких сетей – это инструмент для достижения других целей, например, улучшения точности классификации.
Процедурный вопрос
В данном разделе мы плавно перешли от неглубоких сетей с одним скрытым слоем до многослойных свёрточных сетей. Всё казалось так легко! Мы внесли изменение, и получили улучшение. Если вы начнёте экспериментировать, то гарантирую, что обычно всё будет идти не так гладко. Я представил вам причёсанный рассказ, опуская множество экспериментов, в том числе и неудачных. Надеюсь, что этот причёсанный рассказ поможет вам яснее понять базовые идеи. Но он рискует передать неполное впечатление. Получение хорошей, рабочей сети требует множества проб и ошибок, перемежаемых разочарованиями. На практике стоит ожидать огромного количества экспериментов. Для ускорения процесса вам может помочь информация из главы 3 по поводу выбора гиперпараметров сети, а также, возможно, упомянутая там дополнительная литература.
Код для наших свёрточных сетей
Ладно, давайте теперь посмотрим на код нашей программы network3.py. Структурно она похожа на network2.py, которую мы разработали в главе 3, но детали различаются из-за использования библиотеки Theano. Начнём с класса FullyConnectedLayer, похожего на слои, изученные нами ранее.
class FullyConnectedLayer(object):
def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0):
self.n_in = n_in
self.n_out = n_out
self.activation_fn = activation_fn
self.p_dropout = p_dropout
# Initialize weights and biases
self.w = theano.shared(
np.asarray(
np.random.normal(
loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)),
dtype=theano.config.floatX),
name='w', borrow=True)
self.b = theano.shared(
np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)),
dtype=theano.config.floatX),
name='b', borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape((mini_batch_size, self.n_in))
self.output = self.activation_fn(
(1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
self.y_out = T.argmax(self.output, axis=1)
self.inpt_dropout = dropout_layer(
inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
self.output_dropout = self.activation_fn(
T.dot(self.inpt_dropout, self.w) + self.b)
def accuracy(self, y):
"Return the accuracy for the mini-batch."
return T.mean(T.eq(y, self.y_out))Большая часть метода __init__ говорит сама за себя, но несколько примечаний могут помочь прояснить код. Мы, как обычно, случайным образом инициализируем веса и смещения при помощи нормальных случайных значений с подходящими среднеквадратичными отклонениями. Эти строчки выглядят немного непонятно. Однако большая часть странного кода – это загрузка весов и смещений в то, что в библиотеке Theano называется общими переменными. Это гарантирует возможность обработки переменных на GPU, при наличии. Не будем углубляться в этот вопрос – если интересно, почитайте документацию к Theano. Также отметьте, что эта инициализация весов и смещений предназначена для сигмоидной функции активации. В идеале для таких функций, как гиперболический тангенс и ReLU, мы инициализировали бы веса и смещения по-другому. Этот вопрос обсуждается в дальнейших задачах. Метод __init__ заканчивается инструкцией self.params = [self.w, self.b]. Это удобный способ собрать вместе все обучаемые параметры, связанные со слоем. Позже Network.SGD использует атрибуты params, чтобы узнать, какие переменные в экземпляре класса Network могут обучаться.
Метод set_inpt используется для передачи входящих данных слою и вычисления соответствующего выхода. Я пишу inpt вместо input, потому что input – встроенная функция python, и если играться с ними, это может привести к непредсказуемому поведению программ и сложно диагностируемым ошибкам. На самом деле мы передаём входные данные двумя путями: через self.inpt и self.inpt_dropout. Это делается так, поскольку мы можем захотеть использовать исключение во время обучения. А тогда нам нужно будет удалить часть нейронов self.p_dropout. Этим и занимается функция dropout_layer в предпоследней строчке метода set_inpt method. Итак, self.inpt_dropout и self.output_dropout используются во время обучения, а self.inpt и self.output используются для всех других целей, к примеру, оценки точности на подтверждающих [validate] и проверочных [test] данных.
Определения классов ConvPoolLayer и SoftmaxLayer похожи на FullyConnectedLayer. Настолько похожи, что я даже не буду цитировать код. Если вам интересно, полный код программы можно будет изучить позднее в этой главе.
Стоит упомянуть парочку различных деталей. Очевидно, что в ConvPoolLayer и SoftmaxLayer мы вычисляем выходные активации подходящим типу слоя образом. К счастью, в Theano это легко делать, там есть встроенные операции для вычисления свёрток, макс-пулинга и функции softmax.
Менее очевидно, как инициализировать веса и смещения в слое softmax – этого мы не обсуждали. Мы упоминали, что для сигмоидных слоёв веса нужно инициализировать соответствующим образом параметризированные нормальные случайные распределения. Но этот эвристический аргумент относился к сигмоидным нейронам (и, с небольшими поправками, к танг-нейронам). Однако нет особых причин для того, чтобы этот аргумент был применим к softmax-слоям. Поэтому нет каких-то причин, чтобы априори применять такую инициализацию снова. Вместо этого я инициализирую все веса и смещения в 0. Вариант спонтанный, но на практике работает неплохо.
Итак, мы изучили все классы слоёв. Что насчёт класса Network? Начнём с изучения метода __init__:
class Network(object):
def __init__(self, layers, mini_batch_size):
"""Принимает список слоёв layers, описывающий архитектуру сети, и значение
mini_batch_size для использования во время обучения через стохастический
градиентный спуск
"""
self.layers = layers
self.mini_batch_size = mini_batch_size
self.params = [param for layer in self.layers for param in layer.params]
self.x = T.matrix("x")
self.y = T.ivector("y")
init_layer = self.layers[0]
init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
for j in xrange(1, len(self.layers)):
prev_layer, layer = self.layers[j-1], self.layers[j]
layer.set_inpt(
prev_layer.output, prev_layer.output_dropout, self.mini_batch_size)
self.output = self.layers[-1].output
self.output_dropout = self.layers[-1].output_dropoutБольшая часть кода говорит сама за себя. Строчка self.params = [param for layer in ...] собирает все параметры для каждого слоя в единый список. Как предполагалось ранее, метод Network.SGD использует self.params, чтобы понять, какие параметры из Network сеть может выучить. Строки self.x = T.matrix(«x») и self.y = T.ivector(«y») определяют символические переменные Theano x и y. Они будут представлять вход и желаемый выход сети.
Это не обучающий материал по использованию Theano, поэтому я не буду углубляться в то, что означают символические переменные (см. документацию, и также одну из обучающих статей). Грубо говоря, они обозначают математические переменные, а не конкретные. С ними можно проводить многие обычные операции: складывать, вычитать, умножать, применять функции, и так далее. Theano предоставляет много возможностей для манипулирования подобными символическими переменными, проведения свёрток, макс-пулинга и так далее. Однако главное – возможность быстрого символического дифференцирования при помощи очень общей формы алгоритма обратного распространения. Это чрезвычайно полезно для применения стохастического градиентного спуска к широкому спектру архитектур сети. В частности, следующие строки кода определяют символический выход сети. Начинаем мы, назначая входные данные первому слою:
init_layer.set_inpt(self.x, self.x, self.mini_batch_size)Входные данные передаются по одному мини-пакету за раз, поэтому там и указан его размер. Мы передаём входные данные self.x два раза: дело в том, что мы можем использовать сеть двумя разными способами (с исключением или без него). Цикл for распространяет символическую переменную self.x вперёт по слоям Network. Это позволяет нам определять итоговые атрибуты output и output_dropout, символически представляющие выходные данные Network.
Разобравшись с инициализацией Network, посмотрим на её обучение через метод SGD. Код выглядит длинным, но его структура довольно проста. Пояснения идут после кода:
def SGD(self, training_data, epochs, mini_batch_size, eta,
validation_data, test_data, lmbda=0.0):
"""Обучить сеть при помощи мини-пакетов и стохастического градиентного
спуска."""
training_x, training_y = training_data
validation_x, validation_y = validation_data
test_x, test_y = test_data
# вычислить количество мини-пакетов для обучения, проверки и подтверждения
num_training_batches = size(training_data)/mini_batch_size
num_validation_batches = size(validation_data)/mini_batch_size
num_test_batches = size(test_data)/mini_batch_size
# задать регуляризированную функцию стоимости, символические градиенты и обновления
l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
cost = self.layers[-1].cost(self)+\
0.5*lmbda*l2_norm_squared/num_training_batches
grads = T.grad(cost, self.params)
updates = [(param, param-eta*grad)
for param, grad in zip(self.params, grads)]
# определить функции для обучения мини-пакета и для вычисления
# точности при подтверждении и проверке мини-пакетов.
i = T.lscalar() # mini-batch index
train_mb = theano.function(
[i], cost, updates=updates,
givens={
self.x:
training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
validate_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
test_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
self.test_mb_predictions = theano.function(
[i], self.layers[-1].y_out,
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
# Пошло само обучение
best_validation_accuracy = 0.0
for epoch in xrange(epochs):
for minibatch_index in xrange(num_training_batches):
iteration = num_training_batches*epoch+minibatch_index
if iteration
print("Training mini-batch number {0}".format(iteration))
cost_ij = train_mb(minibatch_index)
if (iteration+1)
validation_accuracy = np.mean(
[validate_mb_accuracy(j) for j in xrange(num_validation_batches)])
print("Epoch {0}: validation accuracy {1:.2
epoch, validation_accuracy))
if validation_accuracy >= best_validation_accuracy:
print("This is the best validation accuracy to date.")
best_validation_accuracy = validation_accuracy
best_iteration = iteration
if test_data:
test_accuracy = np.mean(
[test_mb_accuracy(j) for j in xrange(num_test_batches)])
print('The corresponding test accuracy is {0:.2
test_accuracy))
print("Finished training network.")
print("Best validation accuracy of {0:.2
best_validation_accuracy, best_iteration))
print("Corresponding test accuracy of {0:.2Первые строчки понятны, они разделяют наборы данных на компоненты x и y, и вычисляют количество мини-пакетов, используемых в каждом наборе данных. Следующие строчки поинтереснее, и они демонстрируют, почему с библиотекой Theano так интересно работать. Процитирую их здесь:
# задать регуляризированную функцию стоимости, символические градиенты и обновления
l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
cost = self.layers[-1].cost(self)+\
0.5*lmbda*l2_norm_squared/num_training_batches
grads = T.grad(cost, self.params)
updates = [(param, param-eta*grad)
for param, grad in zip(self.params, grads)]В этих строках мы символически определяем регуляризованную функцию стоимости на основе логарифмической функции правдоподобия, вычисляем соответствующие производные в функции градиента, а также соответствующие обновления параметров. Theano позволяет нам сделать всё это всего в нескольких строках. Спрятано только то, что вычисление стоимости включает в себя вызов метода стоимости для выходного слоя; этот код находится в другом месте network3.py. Но он краткий и простой. С определением всего этого всё готово для определения функции train_mb, символической функции Theano, использующей обновления для обновления параметров Network по индексу мини-пакета. Сходным образом функции validate_mb_accuracy и test_mb_accuracy вычисляют точность Network на любом заданном мини-пакете подтверждающих или проверочных данных. Усредняя по этим функциям, мы можем подсчитывать точность на подтверждающем и проверочном наборах данных целиком.
Оставшаяся часть метода SGD говорит сама за себя – мы просто последовательно проходим по эпохам, снова и снова обучая сеть на мини-пакетах обучающих данных, и подсчитываем точность подтверждения и проверки.
Теперь мы поняли наиболее важные части года network3.py. Давайте кратко пройдёмся по программе целиком. Не обязательно изучать её всю подробно, но вам может понравиться пробежаться по верхам, и, возможно, углубляться в какие-то особенно понравившиеся отрывки. Но, конечно, лучший способ понять программу – изменять её, добавлять что-то новое, рефакторить те части, которые, по вашему мнению, можно улучшить. После кода привожу несколько задач, содержащих ряд начальных предложений по тому, что тут можно сделать. Вот код.
"""network3.py
~~~~~~~~~~~~~~
Программа на основе библиотеки Theano для обучения и запуска простых нейросетей.
Поддерживает несколько типов слоёв (полносвязный, свёрточный, макс-пулинг, softmax) и функций активации (сигмоида, гиперболический тангенс, ReLU; легко добавлять новые).
В работе на CPU программа показала себя гораздо быстрее, чем network.py и network2.py. Но, в отличие от них, её можно запускать и на GPU, что будет ещё быстрее.
Поскольку код основан на Theano, он во многих местах отличается от network.py и network2.py. Где возможно, я пытался делать код похожим на предыдущие. В частности, API похоже на network2.py. Я сконцентрировался на упрощении и читаемости кода, на том, чтобы его легко было менять. Он не оптимизирован, в нём нет многого того, что хотелось бы добавить.
Программа включает идеи из документации Theano для ГСС (http://deeplearning.net/tutorial/lenet.html ), из реализации исключения от Миша Денил (https://github.com/mdenil/dropout ) и из кода Криса Олаха (http://colah.github.io ).
Написано для Theano 0.6 и 0.7, для более поздних версий требуется небольшая адаптация.
"""
#### Библиотеки
# Стандартная
import cPickle
import gzip
# Сторонние
import numpy as np
import theano
import theano.tensor as T
from theano.tensor.nnet import conv
from theano.tensor.nnet import softmax
from theano.tensor import shared_randomstreams
from theano.tensor.signal import downsample
# Функции активации нейронов
def linear(z): return z
def ReLU(z): return T.maximum(0.0, z)
from theano.tensor.nnet import sigmoid
from theano.tensor import tanh
#### Константы
GPU = True
if GPU:
print "Trying to run under a GPU. If this is not desired, then modify "+\
"network3.py\nto set the GPU flag to False."
try: theano.config.device = 'gpu'
except: pass # it's already set
theano.config.floatX = 'float32'
else:
print "Running with a CPU. If this is not desired, then the modify "+\
"network3.py to set\nthe GPU flag to True."
#### Загрузка базы MNIST
def load_data_shared(filename="../data/mnist.pkl.gz"):
f = gzip.open(filename, 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
def shared(data):
"""Размещаем данные в общих переменных. Это позволяет Theano копировать данные в GPU, если таковой есть.
"""
shared_x = theano.shared(
np.asarray(data[0], dtype=theano.config.floatX), borrow=True)
shared_y = theano.shared(
np.asarray(data[1], dtype=theano.config.floatX), borrow=True)
return shared_x, T.cast(shared_y, "int32")
return [shared(training_data), shared(validation_data), shared(test_data)]
#### Главный класс для создания и обучения сетей
class Network(object):
def __init__(self, layers, mini_batch_size):
"""Принимает список слоёв layers, описывающий архитектуру сети, и значение
mini_batch_size для использования во время обучения через стохастический
градиентный спуск.
"""
self.layers = layers
self.mini_batch_size = mini_batch_size
self.params = [param for layer in self.layers for param in layer.params]
self.x = T.matrix("x")
self.y = T.ivector("y")
init_layer = self.layers[0]
init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
for j in xrange(1, len(self.layers)):
prev_layer, layer = self.layers[j-1], self.layers[j]
layer.set_inpt(
prev_layer.output, prev_layer.output_dropout, self.mini_batch_size)
self.output = self.layers[-1].output
self.output_dropout = self.layers[-1].output_dropout
def SGD(self, training_data, epochs, mini_batch_size, eta,
validation_data, test_data, lmbda=0.0):
"""Обучить сеть при помощи мини-пакетов и стохастического градиентного
спуска."""
training_x, training_y = training_data
validation_x, validation_y = validation_data
test_x, test_y = test_data
# вычислить количество мини-пакетов для обучения, проверки и подтверждения
num_training_batches = size(training_data)/mini_batch_size
num_validation_batches = size(validation_data)/mini_batch_size
num_test_batches = size(test_data)/mini_batch_size
# задать регуляризированную функцию стоимости, символические градиенты и обновления
l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
cost = self.layers[-1].cost(self)+\
0.5*lmbda*l2_norm_squared/num_training_batches
grads = T.grad(cost, self.params)
updates = [(param, param-eta*grad)
for param, grad in zip(self.params, grads)]
# определить функции для обучения мини-пакета и для вычисления
# точности при подтверждении и проверке мини-пакетов.
i = T.lscalar() # mini-batch index
train_mb = theano.function(
[i], cost, updates=updates,
givens={
self.x:
training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
validate_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
test_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
self.test_mb_predictions = theano.function(
[i], self.layers[-1].y_out,
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
# Пошло само обучение
best_validation_accuracy = 0.0
for epoch in xrange(epochs):
for minibatch_index in xrange(num_training_batches):
iteration = num_training_batches*epoch+minibatch_index
if iteration % 1000 == 0:
print("Training mini-batch number {0}".format(iteration))
cost_ij = train_mb(minibatch_index)
if (iteration+1) % num_training_batches == 0:
validation_accuracy = np.mean(
[validate_mb_accuracy(j) for j in xrange(num_validation_batches)])
print("Epoch {0}: validation accuracy {1:.2%}".format(
epoch, validation_accuracy))
if validation_accuracy >= best_validation_accuracy:
print("This is the best validation accuracy to date.")
best_validation_accuracy = validation_accuracy
best_iteration = iteration
if test_data:
test_accuracy = np.mean(
[test_mb_accuracy(j) for j in xrange(num_test_batches)])
print('The corresponding test accuracy is {0:.2%}'.format(
test_accuracy))
print("Finished training network.")
print("Best validation accuracy of {0:.2%} obtained at iteration {1}".format(
best_validation_accuracy, best_iteration))
print("Corresponding test accuracy of {0:.2%}".format(test_accuracy))
#### Определение типов слоёв
class ConvPoolLayer(object):
"""Создаёт комбинацию из свёрточного и макс-пулинг слоёв. Более сложный вариант
программы разделял бы эти слои, но для наших целей мы всегда используем их вместе,
и это упрощает код, поэтому имеет смысл.
"""
def __init__(self, filter_shape, image_shape, poolsize=(2, 2),
activation_fn=sigmoid):
"""`filter_shape` - кортеж длины 4, содержит количество фильтров, количество входящих карт признаков, высоту фильтра и ширину фильтра.
`image_shape` - кортеж длины 4, содержит размер мини-пакета, количество входящих карт признаков, высоту и ширину изображения.
`poolsize` - кортеж длины 2, содержит размеры пулинга y и x.
"""
self.filter_shape = filter_shape
self.image_shape = image_shape
self.poolsize = poolsize
self.activation_fn=activation_fn
# initialize weights and biases
n_out = (filter_shape[0]*np.prod(filter_shape[2:])/np.prod(poolsize))
self.w = theano.shared(
np.asarray(
np.random.normal(loc=0, scale=np.sqrt(1.0/n_out), size=filter_shape),
dtype=theano.config.floatX),
borrow=True)
self.b = theano.shared(
np.asarray(
np.random.normal(loc=0, scale=1.0, size=(filter_shape[0],)),
dtype=theano.config.floatX),
borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape(self.image_shape)
conv_out = conv.conv2d(
input=self.inpt, filters=self.w, filter_shape=self.filter_shape,
image_shape=self.image_shape)
pooled_out = downsample.max_pool_2d(
input=conv_out, ds=self.poolsize, ignore_border=True)
self.output = self.activation_fn(
pooled_out + self.b.dimshuffle('x', 0, 'x', 'x'))
self.output_dropout = self.output # no dropout in the convolutional layers
class FullyConnectedLayer(object):
def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0):
self.n_in = n_in
self.n_out = n_out
self.activation_fn = activation_fn
self.p_dropout = p_dropout
# Initialize weights and biases
self.w = theano.shared(
np.asarray(
np.random.normal(
loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)),
dtype=theano.config.floatX),
name='w', borrow=True)
self.b = theano.shared(
np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)),
dtype=theano.config.floatX),
name='b', borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape((mini_batch_size, self.n_in))
self.output = self.activation_fn(
(1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
self.y_out = T.argmax(self.output, axis=1)
self.inpt_dropout = dropout_layer(
inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
self.output_dropout = self.activation_fn(
T.dot(self.inpt_dropout, self.w) + self.b)
def accuracy(self, y):
"Return the accuracy for the mini-batch."
return T.mean(T.eq(y, self.y_out))
class SoftmaxLayer(object):
def __init__(self, n_in, n_out, p_dropout=0.0):
self.n_in = n_in
self.n_out = n_out
self.p_dropout = p_dropout
# Инициализация весов и смещений
self.w = theano.shared(
np.zeros((n_in, n_out), dtype=theano.config.floatX),
name='w', borrow=True)
self.b = theano.shared(
np.zeros((n_out,), dtype=theano.config.floatX),
name='b', borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape((mini_batch_size, self.n_in))
self.output = softmax((1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
self.y_out = T.argmax(self.output, axis=1)
self.inpt_dropout = dropout_layer(
inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
self.output_dropout = softmax(T.dot(self.inpt_dropout, self.w) + self.b)
def cost(self, net):
"Вернуть логарифмическую функцию правдоподобия."
return -T.mean(T.log(self.output_dropout)[T.arange(net.y.shape[0]), net.y])
def accuracy(self, y):
"Вернуть точность мини-пакета."
return T.mean(T.eq(y, self.y_out))
#### Разное
def size(data):
"Вернуть размер набора данных `data`."
return data[0].get_value(borrow=True).shape[0]
def dropout_layer(layer, p_dropout):
srng = shared_randomstreams.RandomStreams(
np.random.RandomState(0).randint(999999))
mask = srng.binomial(n=1, p=1-p_dropout, size=layer.shape)
return layer*T.cast(mask, theano.config.floatX)Задачи
- В текущем виде метод SGD требует вручную выбрать количество эпох для обучения. В книге мы уже обсуждали автоматический способ выбора количества эпох для обучения, раннюю остановку. Измените network3.py так, чтобы программа могла делать раннюю остановку.
- Добавьте в Network метод, возвращающий точность на основе произвольного набора данных.
- Измените SGD так, чтобы можно было задавать скорость обучения η как функцию от номера эпохи (поработав над этой задачей, вы, вероятно, найдёте интересным обсуждение по ссылке).
- Ранее в этой главе я описал технику расширения обучающего набора через применение небольших вращений, искажений и переносов. Измените network3.py, включив в неё все эти техники. Учтите, что если только у вас нет огромного количества памяти, нет смысла генерировать новые данные целиком. Стоит рассмотреть альтернативные варианты.
- Добавьте возможность загрузки и сохранения сетей.
- Недостаток текущего кода – малое количество инструментов для диагностики. Можете ли вы придумать, какую диагностику стоит добавить, чтобы понять, насколько сеть переобучается? Добавьте её.
- Мы использовали для ReLU ту же технику инициализации, что и для сигмоидных (и танг-) нейронов. Оправдание такой инициализации относилось конкретно к сигмоиде. Рассмотрите сеть, полностью состояющую из ReLU (включая выход). Покажите, что масштабирование всех весов сети на константу c>0 просто масштабирует выход в c L−1 раз, где L – количество слоёв. Что изменится, если последний слой будет softmax? Что думаете по поводу использования сигмоидной инициализации для ReLU? Сможете ли вы придумать процедуру инициализации получше? Отмечу, что это открытая проблема, которая не имеет простого и всеобъемлющего ответа. Однако её разработка поможет вам лучше понимать сети, состоящие из ReLU.
- Наш анализ проблемы нестабильного градиента относился к сигмоидным нейронам. Как изменится анализ в случае, когда сеть будет состоять из ReLU? Можете ли вы придумать хороший способ изменения такой сети, чтобы она не страдала от проблемы нестабильного градиента? Примечание: слово «хороший» подразумевает некие исследования. Довольно легко придумать способы провести такие изменения – однако я недостаточно плотно занимался такими исследованиями, чтобы найти какую-нибудь по-настоящему хорошую технологию.