Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Всем привет! Обычно, когда я собираю корзину в супермаркете, я беру продукты по очереди в том порядке, в каком они находятся в списке. Недавно я шел по магазину и, наворачивая очередной круг в поисках товара, который лежит в отделе, где я уже был, я подумал, можно было бы сэкономить уйму времени составляя список так, чтобы, собирая продукты подряд, я бы шел по оптимальному маршруту, не прилагая умственных усилий. Сперва я хотел заранее составлять список таким образом, но это сложно и неинтересно, так что я решил автоматизировать этот процесс и вот что из этого вышло:

Задумка такая: сперва берем исходный неотсортированный список и группируем в нем продукты по категориям (мясо, молочка и т.д.) затем, зная отделы, куда предстоит зайти, и их расположение, строим оптимальный маршрут через заданные точки. После этого располагаем группы товаров в соответствии с очередностью посещения отделов. Плюсом к этому нужен будет какой-то интерфейс, так как вести список покупок в виде питоновского списка неудобно, в качестве такого интерфейса я решил использовать телеграм-бота.
Группируем товары
Для примера будем использовать вот такой список:
Творог Тушенка Бананы Фундук Фарш Хлеб Яйца Пиво Хлопья Яблоки Перец Кетчуп Котлеты Лимонад Мороженное
Начнем с того, что составим перечень отделов в магазине. Для этого я пошел в ближайший перекресток и составил таблицу такого типа:
Имя | x | y | Вход |
Выпечка | 15 | 3 | хлеб, плюшка, булка |
Орехи | 15 | 2 | орех |
Напитки | 7 | 4 | напитки |
Заморозка | 1 | 4 | мороженое, пельмени, заморозка |
Первая колонка содержит название отдела, вторая и третья – его координаты в условных единицах измерения, последняя колонка содержит примеры товаров, которые там продаются. На первых порах я хотел в последней колонке перечислить вообще всё, что я обычно там покупаю, тогда группировать будет легко, достаточно посмотреть к какому отделу относится каждый товар из списка и всё. Этот подход имеет несколько минусов. Во-первых, если появится что-то новое – этот товар придется всякий раз руками добавлять в таблицу, что неудобно. Во-вторых, даже одно и то же можно записать по-разному, скажем можно написать греча или гречка, горох или горошек все варианты перебирать тоже не хотелось.
Решение нашлось такое: вместо слов можно оперировать эмбеддингами. Эмбеддинги - очень удобный инструмент, они позволяют работать не со строками, а с векторами, отражающими их смысл. Например, чтобы определить, насколько два слова близки по смыслу можно посчитать норму разности соответствующих им векторов. Разность векторов, соответствующих словам 'Напитки' и 'Пиво' будет намного меньше разности векторов для слов 'Хлеб' и 'Пиво', так можно понять, что пиво можно купить скорее в отделе напитков, чем в хлебном.
Я пользовался русскоязычными эмбеддингами Navec. Он содержит 500 тысяч слов, и имеет библиотеку, которая предоставляет удобный интерфейс в виде питоновского словаря. Слово используется в качестве ключа, по которому возвращается вектор из 300 значений.
Теперь алгоритм немного изменился, для каждой позиции в списке измеряем ее близость с примерами продуктов из четвертой колонки и относим ее к тому отделу, где содержится пример наиболее близкий по смыслу. Это позволяет решить проблему с новыми позициями и с разными написаниями одних и тех же продуктов: эмбеддинги для 'гороха' и для 'горошка' практически одинаковые. Итого, получаем такой словарь:
{'Выпечка': ['Хлеб'],
'Завтраки': ['Хлопья'],
'Консервы': ['Тушенка'],
'Молоко/Сыр/Яйца': ['Творог', 'Яйца'],
'Мясо': ['Фарш', 'Котлеты'],
'Напитки': ['Пиво', 'Лимонад'],
'Овощи/Фрукты': ['Бананы', 'Яблоки'],
'Орехи': ['Фундук'],
'Приправы': ['Перец', 'Кетчуп']}
Обратите внимание, что фундук попал в орехи, хотя фундука нет среди примеров товаров этого отдела.
Строим оптимальный маршрут
Координаты из 2 и 3 столбцов преобразуем в матрицу смежности M так, что элемент M(i,j) содержит расстояние от отдела i до отдела j. В моем случае визуализация матрицы смежности выглядит так:
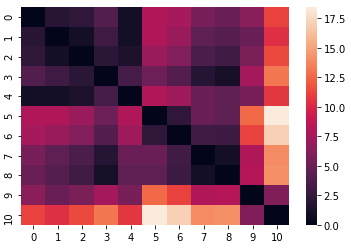
Поскольку товары уже сопоставлены с отделами, в матрицу попадают только отделы, в которые я планирую заходить. В данном случае 11 отделов.
Далее надо построить оптимальный маршрут. Первая мысль - применить жадный алгоритм, т.е. из каждого отдела идем в тот, который ближе всего. Но такой подход не всегда дает оптимальный результат. Ниже простой пример, где надо обойти 4 точки, стартуя из точки А. Для кратчайшего пути надо сперва посетить не самую ближнюю точку.

Будем использовать динамическое программирование. Создадим матрицу A размером n ⨉ 2ⁿ где n - количество отделов. Матрица будет содержать длины кратчайших путей, проходящих через точки, соответствующие столбцу матрицы и заканчивающихся в точке, соответствующей строке матрицы. Номер столбца кодирует маршрут в виде битовой маски.
Поясню на примере. Предположим A(5,1105) = 10. 1105 в переводе в двоичную систему будет 10001010001, это значит что мы посетили отделы 1, 5, 7 и 11, которые соответствуют единицам. Номер строки 5 - говорит о том, что последней мы посетили точку №5. Соответственно, маршрут минимальной длинны через точки 1,5,7 и 11 с конечным пунктом в точке 5 имеет длину 10.
Сначала заполняем столбцы, содержащие только одну единицу в двоичном представлении — это пути, состоящие из одной точки. Затем столбцы, содержащие две единицы, три и т.д. Заполняем по мере увеличения количества единиц в номере столбца, т.к. для вычисления их значений используются предыдущие заполненные столбцы.
К примеру, столбцы, содержащие 1 и 2 единицы уже заполнены, и мы хотим вычислить значение первой строки 15 столбца. Переводим 15 в двоичную систему получаем 1101. Значит мы ищем длину минимального маршрута через точки 1,2 и 4, оканчивающийся в точке 1.
Он равен минимальному из 2 значений, M(1,2) + A(2, 5) и M(1,4) + A(4, 5). Тут мы смотрим на 5 столбец, так как в двоичном представлении он имеет вид 0101 то есть предыдущее состояние перед искомым. Так заполняем все клетки. Клетки, соответствующие невозможному состоянию, заполняем бесконечными значениями.
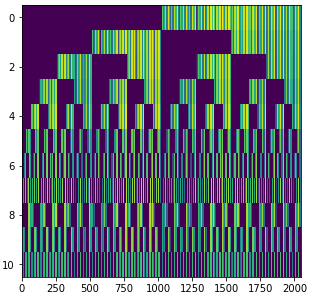
В итоге нас интересует последний столбец. Он соответствует ситуации, когда мы обошли все точки маршрута. Выбираем минимальное значение в столбце и с помощью матрицы строим маршрут.
Тут я решил сделать небольшую доработку. В случае, если среди категорий присутствует заморозка, мы всегда строим маршрут так, чтобы он оканчивался в этом отделе. Так у замороженных продуктов меньше шансов растаять.
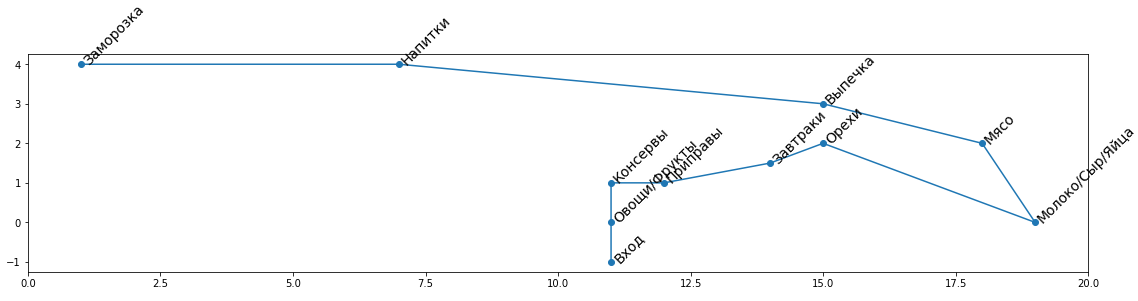

Интересно как маршрут полностью перестраивается в зависимости от того есть в списке заморозка или нет. Видно, что решение получается гораздо оптимальнее, чем просто прокладка маршрута без учета заморозки и заход в этот отдел в конце.
Пишем телеграм-бота
Про то как сделать телеграм-бота написано много статей, я расскажу про основные моменты.
В качестве хостинга я выбрал google cloud platform, там я создал виртуальную машину на Debian, и установил на нее:
- python3 – на нем написан весь код,
- git – чтобы было удобно накатывать изменения,
- mySQL – там будут храниться списки покупок,
- tmux – чтобы бот не выключался при закрытии ssh-сессии.
Для взаимодействия с api телеграма используется библиотека aiogram.
Бот понимает всего 3 команды: /del# - удаляет позицию # из списка /clear - очистить список /sort - показать отсортированный список
Если бот получает сообщение без команды, оно воспринимается как позиция для занесения в список.
Когда к боту подключается новый пользователь в базе данных создается таблица user_xxxxxxxx, где xxxxxxxx - id пользователя в телеграме, далее весь список, будет храниться в этой таблице.

Вот такой результат, спасибо, что дочитали до конца, ссылка на проект на github https://github.com/Megachell/ListOptimizerBot





