Оптимизация цен на основе эластичности

Статья подготовлена для конференции Aha'22 и рассказывает про задачу выставления оптимальных цен. Я в последнее время работал над этой задачей в Яндекс Маркете и попробовал выписать ряд вещей, которые мне видятся важными в контексте этой задачи. Раньше я занимался задачами, связанными с Машинным Обучением (Machine Learning, ML) в рекламных технологиях, и ещё год назад тема ценообразования для меня была абсолютно новой. Соответственно, мне было важно разобраться с терминологией, возможностью применения ML для ценообразования, алгоритмами вычисления оптимальных цен на основе кривых спроса, а также выписать формулы оптимальных цен для каких-то частных случаев. Надеюсь, это будет кому-то интересно и полезно.

Возможно, я что-то не понимаю и упускаю что-то важное, пишите про это в комментариях.

Ценообразование в Яндекс Маркете

Яндекс Маркет – это маркетплейс, в котором десятки тысяч продавцов могут размещать свои товары. Продавцы сами решают какие товары продавать и по каким ценам. Но иногда Яндекс Маркет сам выступает одним из таких продавцов. И именно для продающихся таким способом товаров Маркет имеет возможность выставлять свои цены.

Что такое кривая спроса и эластичность?

Кривая спроса – это то, как продажи зависят от цены. Чем меньше цена, тем больше продаж и наоборот.

Кривая спроса – это очень важная для бизнеса штука, так как она определяет то, какую цену нужно ставить на товар, чтобы достичь той или иной бизнес цели. Большая часть бизнесов думают о прибыли и поэтому задача формулируется как

Зная кривые спроса для каждого товара, найти такие цены, которые максимизируют совокупную прибыль.

И тут сразу озвучу моменты, которые всплывают в голове у бывалых трейд маркетологов:

• Как получить эти знания о кривых? Есть целый ряд сложностей:

  • Позиций много, несколько тысяч, а у кого-то и под миллион.

  • Кривые меняются во времени.

  • Иногда это не гладкие кривые, а ступенчатые функции, и ступеньки находятся в точках цен конкурентов, и получается, что нужно мониторить эти цены, а это целая наука. Иногда конкуренты имеют другие цены и другие условия доставки, гарантийный срок, свежесть и могут иметь другой уровень сервиса поддержки. И это важно учитывать.

  • Спрос на товар зависит не только от его цены, но и от цен на соседние товары; можно привлечь покупателей скидками на избранный набор товаров, а продажи поднимутся на всех товарах.

• Даже если кривая известна, то задача не просто максимизировать прибыль. Есть ряд дополнительных аспектов оптимального ценообразования:

  • кумулятивный price perсeption от всех товаров;

  • захват рынка (важна не только прибыль, но и суммарный оборот);

  • сроки годности и распродажа устаревающих моделей;

  • распродажа "дедстоков" (запасов, которые давно лежат на стоке, и видимо, уже не продадутся по текущей цене).

Здесь хочется написать фразу "we will address these issues later". Я понимаю всю сложность реального мира, и часть этих сложностей нам в Яндексе Маркете удалось учесть в нашей работе над алгоритмизацией ценообразования. То, о чём мне хотелось бы в этой статье рассказать – это

• математическая составляющая задачи выставления оптимальных цен;

• что и как можно сделать с помощью "серебряной пули" 21 века – Machine Learning.

State of Art

Поиск технических и научных статей по темам "Price elasticity prediction" (как обучать/вычислять кривую спроса) и "Price optimization" (как выставлять цену) не привел меня к желаемым результатам. Каких-то готовых рецептов и того, что можно было бы назвать "математическими основами оптимизации цен на базе эластичности", я не нашел (возможно, плохо старался).

Но безусловно, статей про это много и можно найти статьи с правильными общими словами, например:

Machine Learning for Retail Price Optimization: The Price is Right

Using machine learning algorithms to optimize the pricing process is a must for pricing teams of mature retailers with at least thousands of products to reprice regularly. As the technology is gaining popularity in the industry, the ability to manage ML-powered software will soon be an indispensable part of a pricing or category manager’s job description. There’s simply no way around it, as it gives pricing managers the unprecedented level of precision and speed of decision-making across any number of products.

Erik Rodenberg, CEO, Black Wave Consulting Group

Price optimization notebook for apparel retail using Google Vertex AI

The product prices often change based on the observed market response, sell-through rates, supply disruptions, and other factors. Rule based or manual price management in spreadsheets doesn’t scale well to large catalogs with thousands of items. These methods are slow, error prone and can often lead to inventory build up or substantial revenue losses. Machine Learning methods are both faster and provide more formal optimality guarantees. These models can significantly improve the productivity of human experts by allowing them to automate large parts of their decision making process

Встречаются статьи, в которых пишут, что надо использовать современные методы ML, нейросети, градиентные деревья (gradient boosted trees) и тщательно готовить данные.

Встречаются также отдельные страницы с названиями "Калькулятор оптимальных цен" или "Базовые методы оптимизации цен", но в них либо нет формул, либо есть какие-то очень простые и, на мой вкус, странные формулы, которые не открыли мне свою магию. Формул, которые открыли бы мне суть происходящего, давали какие-то новые инсайты, я не нашёл, и ещё раз замечу, что, возможно, дело во мне.

Но возможно (!), что это засекреченное знание. У меня есть конспирологическая теория, что методы получения кривых спроса, а также формулы оптимальных цен тщательно скрываются бизнесами. Можно найти целые "конторы", которые занимаются исключительно вычислением актуальных эластичностей (то, что ниже определяется как производная нормализованных кривых спроса) и продают свою компетенцию выставления оптимальных цен, и им открытость информации ни к чему.

Что ж, в таком случае этот текст и наш доклад на Aha 22 уменьшат степень засекреченности этих знаний, занавес тайны будет будет частично приоткрыт.

Но, независимо от этого, даже если вы готовы покупать у кого-то компетенцию по выставлению оптимальных цен, всё равно хочется понять, а в чём, собственно, сложность, и почему эту задачу нельзя решить за пару месяцев, наняв студента ШАД (или можно?). Давайте разберёмся.

Примеры кривых

Удобно работать с нормализованными кривыми спроса, а именно, с функциями E(r), которые в качестве аргумента имеют нормализованную цену 

r = price / price₀,

а значение функции – это не сами продажи, а множитель к продажам.

То есть, если продажи для цены price₀ равны demand₀, то продажи для цены price – это

demand₀ · E(price / price₀)

то есть

В качестве базовой цены предлагается брать среднюю цену по продажам за последние 4 недели. Вообще, выбор базовой цены – непростой вопрос, от выбора этой цены зависит функция E(r). Хотя есть вариант кривой спроса

в котором выбор базовой цены неважен. Здесь s – это параметр, определяющий эластичность. Здорово, что (заглядывая вперёд) именно это семейство кривых, в определённом смысле, типично, и для большинства товаров кривые спроса в области небольших изменений цен (±30%) можно приблизить кривой из этого семейства с некоторым s.

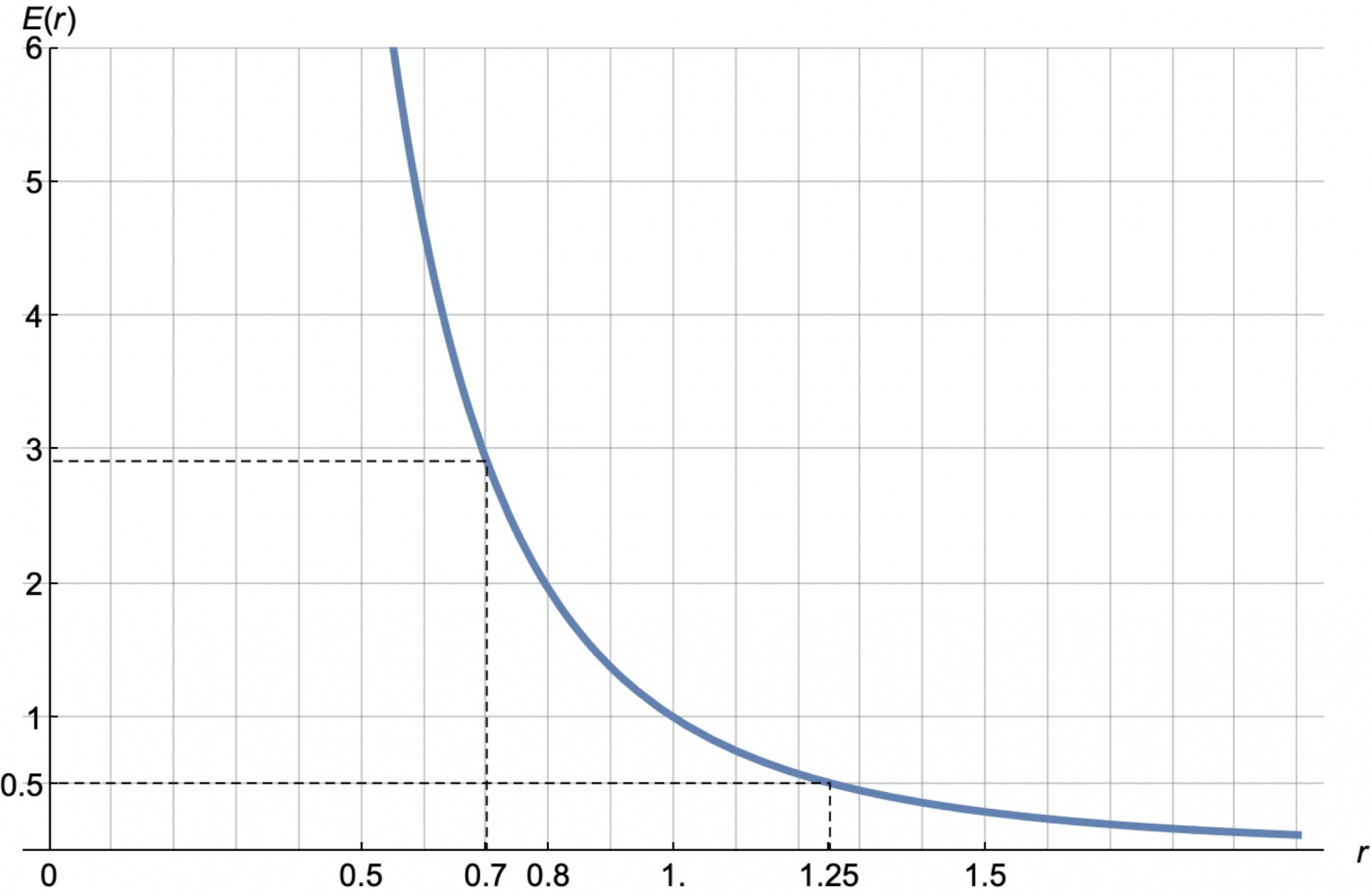
Здесь мы получаем примерно троекратное увеличение продаж при скидке порядка 30% (r=0.7). И падение примерно в 2 раза при наценке 25% (r = 1.25).

Везде дальше под кривой спроса я буду иметь в виду такую нормализованную кривую спроса E(r).

Вот примеры кривых E(r) для реальных продаваемых в Яндекс Маркет товаров. Они были получены с помощью нейросетей, построенных на базе PyTorch:

Верхний график представлен в обычных осях, а нижний в логарифмических (и по оси X и по оси Y). Степенная кривая в логарифмических осях выглядит как прямая. И видно, что некоторые кривые спроса в логарифмических осях очень похожи на прямые, другие выпуклы вниз, а другие – вверх. Соответственно такие кривые мы будем называть степенными (синяя), сверх-степенными (желтая), и суб-степенными (светло-зелёная). А некоторые кривые сложно отнести к одному из этих трёх классов (голубая).

Интерпретация кривой спроса

Видно, что для разных товаров 30%-скидка может повышать продажи в 3, 5, 10 или даже в 50 раз. Желтая кривая на графике выше – это, условно говоря, "Чай", то есть товар,

• покупаемый многими (товар-для-всех);

• регулярно покупаемый;

• с известной нормальной ценой;

• с возможностью быстро сравнивать цены в разных магазинах.

Давайте нарисуем эту кривую отдельно, уже синим цветом:

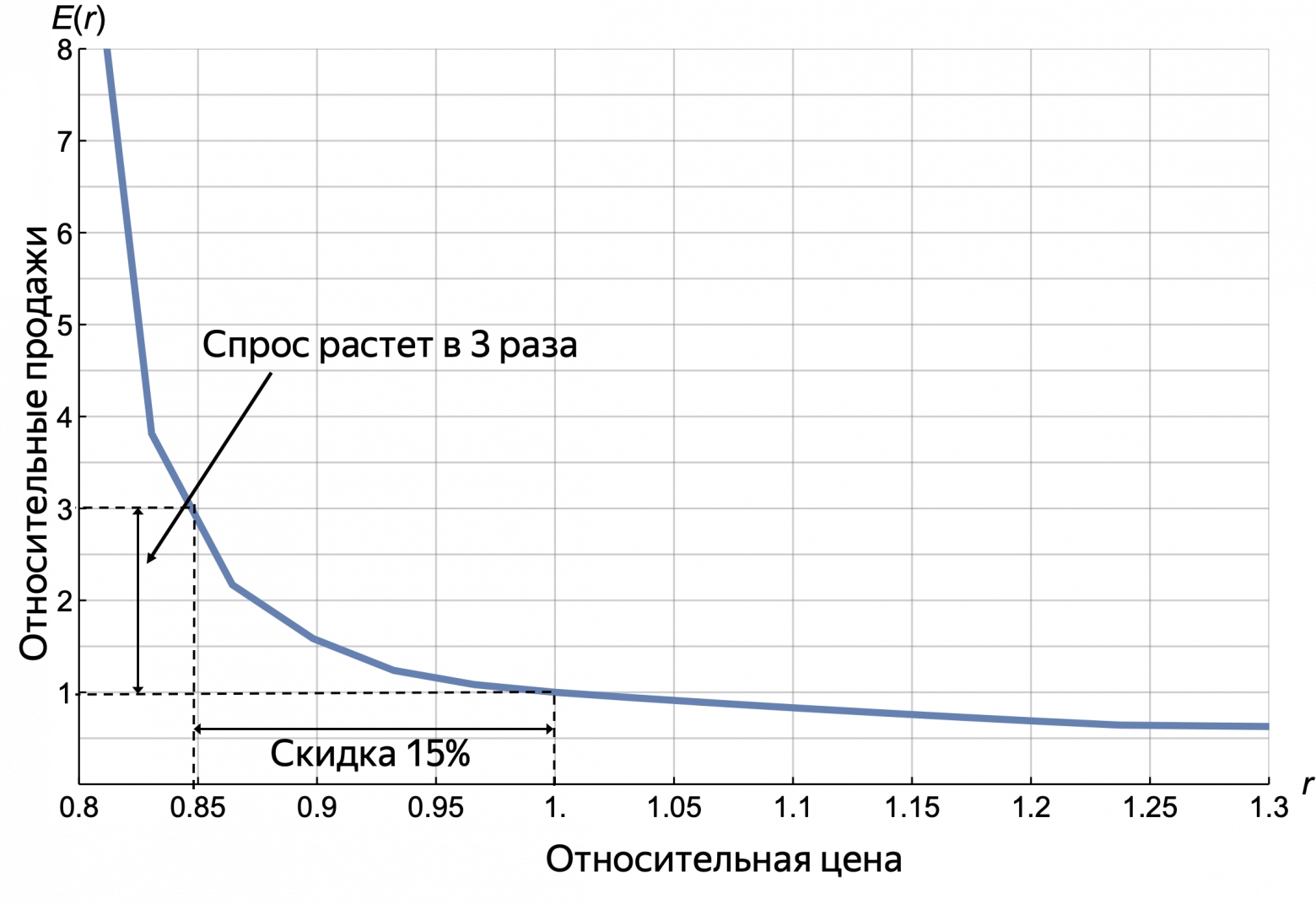
Про эту кривую спроса можно сказать следующее:

• Есть точка резкого роста продаж, точка перегиба (при движении влево) в районе 0.8, то есть в районе скидки -20%. Это область, где мы становимся дешевле конкурента.

• Это товар-герой – он может увеличить продажи и в 50 раз.

• Он слабо эластичный при малых скидках – он дешёвый и пользователи не будут менять маркетплейс из-за условных 10 рублей.

Slope

Первой важной характеристикой нормализованной кривой спроса является сила наклона в точке 1. Обозначим эту силу наклона словом slope. Это и есть эластичность для случая малых скидок / наценок.

Например, slope = 4 означает, что продажи вырастут на 4%, если цену уменьшить на 1%. То есть, буквально, slope – это коэффициент размена процентов продаж на процент изменения цены в области малых движений цен.

Величина slope характеризует кривую лишь в малой окрестности базовой цены. Если ваша задача осторожно "сёрфить", то есть пошагово несильно менять цены, то этого параметра вполне достаточно для поиска оптимальных цен.

Но понятно, что есть множество кривых спроса с одинаковым slope, но по-разному себя ведущих в области больших скидок. Тот же условный "Чай" имеет малый slope в окрестности r = 1, но внезапно вырастает до множителя 12 в районе r = 0.8.

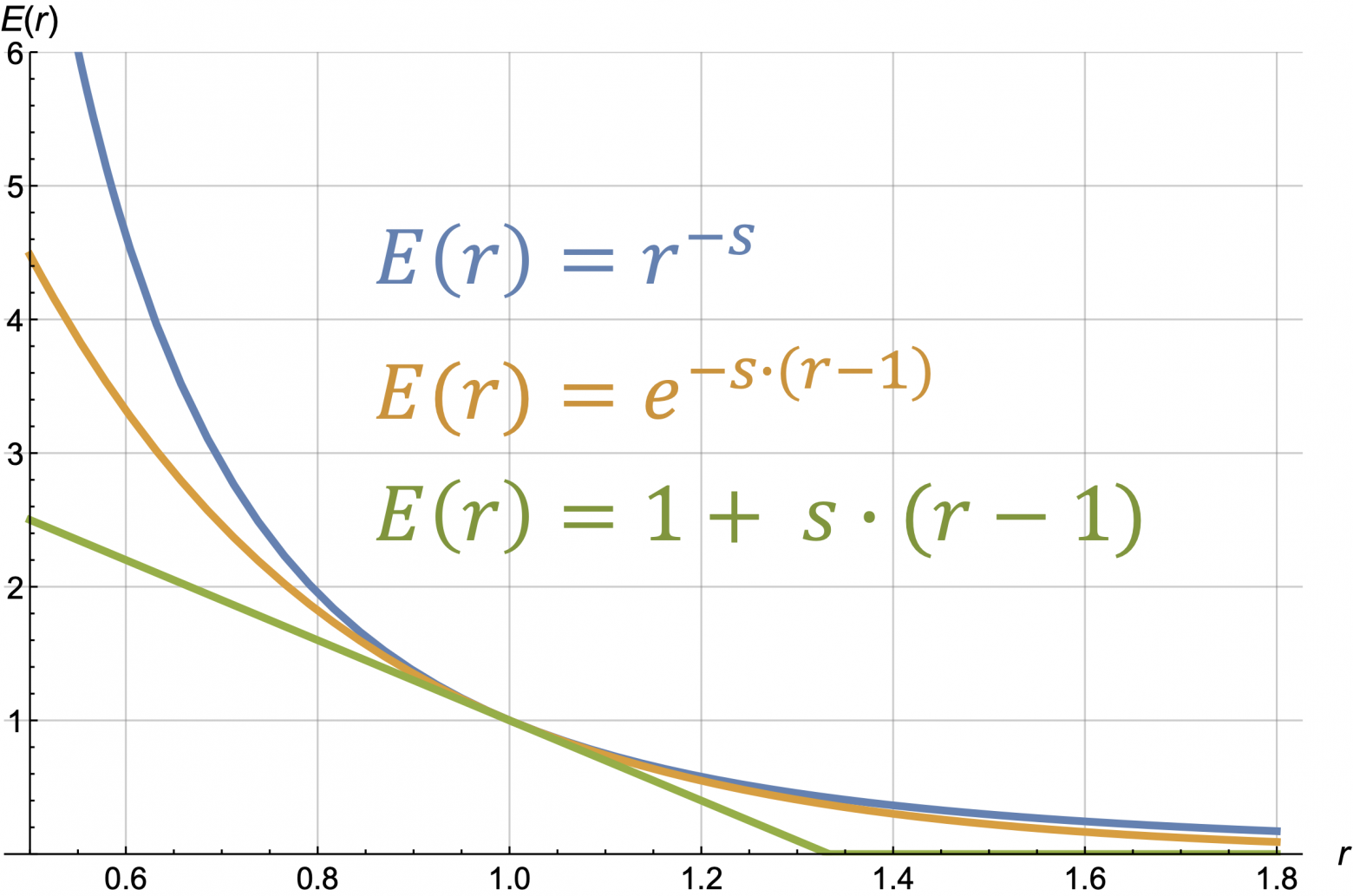
Вот картинка с четырьмя разными кривыми, заданными формулами, c одинаковым значением slope:

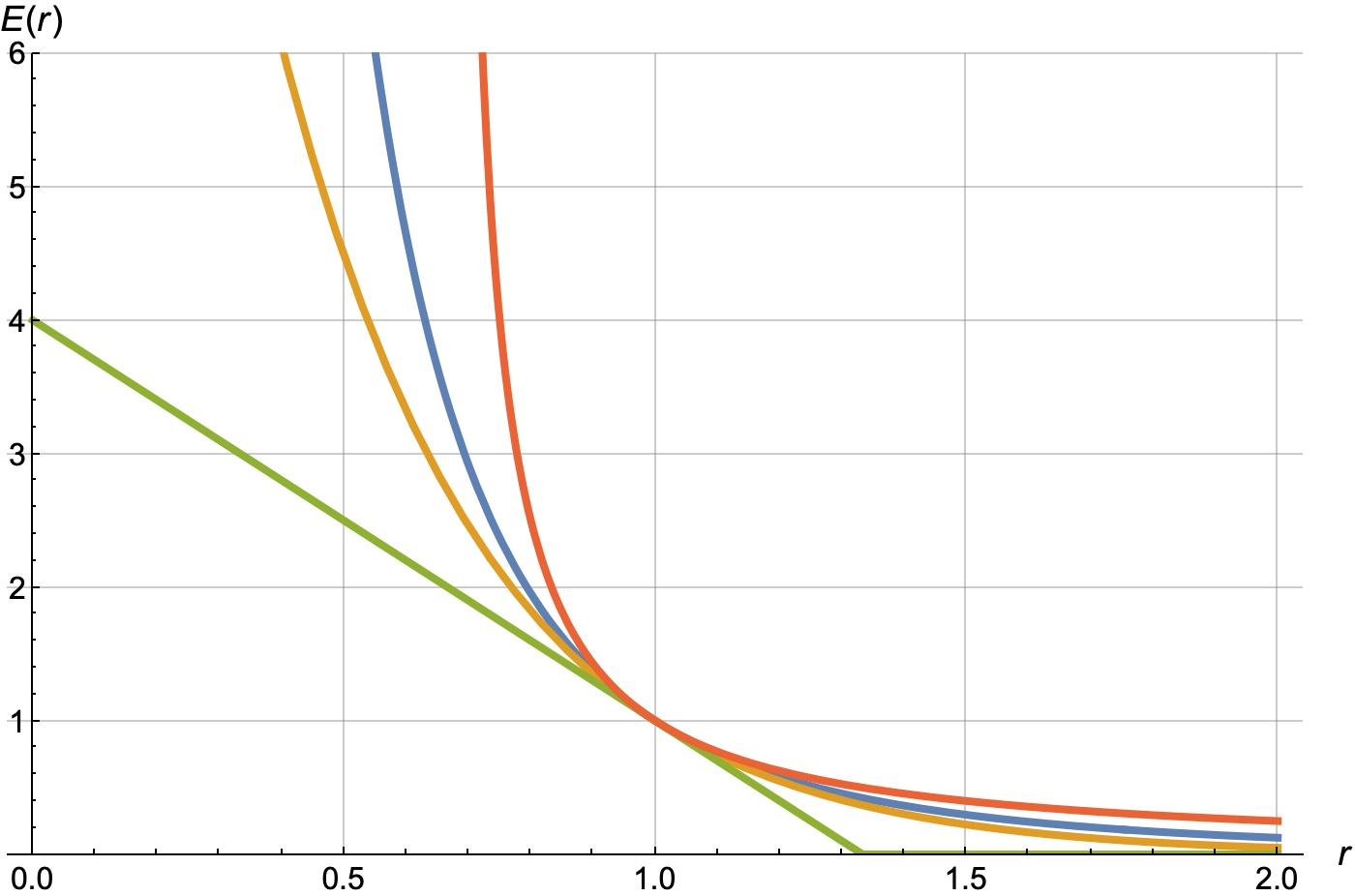
Это простейшие кривые, для которых можно получать формульные результаты, в частности формулу оптимальной цены для максимизации прибыли или комбинации оборота и прибыли (ответы приведены ниже!) (прим. для гиперболической кривой ответы вырожденные и не приведены).

Факторы, влияющие на эластичность

Давайте перечислим основные факторы, влияющие на slope.

• Базовая эластичность. Во-первых, есть некоторое нормальное базовое значение slope для каждого товара. Это то, что характеризует спрос на этот товар в зависимости от цены при некоторых нормальных условиях.

• Ожидаемость скидок. Но есть факторы, которые меняют эластичность. Например, ретейл поводы типа Чёрной Пятницы или праздники могут не только изменить сам спрос, но и поменять кривую эластичности. Ритейл поводы и праздники делают скидки ожидаемыми и увеличивают естественную реакцию на скидки.

• Видимость товара и скидок. Важно, чтобы скидки были хорошо видны. Это и цветные ценники, зачёркнутая цена, разнообразные "плашки" на карточках товаров в интернет магазинах. Можно делать специальные блоки в приложении и на сайте, делать специальное ранжирование в лентах, помещать товары со скидкой на хорошо видимые витрины.

• Понятность. Для промокодов и разных купонов важна понятность условий использования. Должно быть просто их применить и понять размер своей выгоды.

Базовая эластичность в свою очередь раскладывается на другие факторы, но все они касаются уже непосредственно самого товара, его тематической категории, ценовой категории, популярности, актуальности.

Основная мысль здесь такая:

Эластичность – это не фиксированное статическое свойство товара, это то, что меняется и над чем можно и нужно работать.

Термины от группы ДЦО Яндекс Маркета

Величина slope (эластичность) описывает лишь наклон кривой E(r) в точке r = 1. И можно огрубить ситуацию до нескольких классов эластичности, например,

• низкоэластичные: slope ≤ 2

• среднеэластичные: 2 < slope ≤ 4

• высокоэластичные: 4 < slope ≤ 10

• сверхэластичные: slope > 10

Можно также говорить про наклон не только в точке 1, но и конкретизировать размер скидки и говорить про:

Эта величина как раз и называется эластичностью скидки (1 - r) ·100%

Кроме упомянутых выше терминов предлагается использовать ещё такие:

• нечувствительность к малым изменениям: slope < 2 в зоне [0.9, 1.1], но при этом нормальный рост продаж при больших скидках, соответствующий slope > 4

• точки роста:  точки, в окрестности которых кривая имеет большой наклон; обычно там есть точка перегиба, и обычно это происходит в области цены конкурента;

• товары-паровозы: товары, рост продаж которых влечёт рост продаж N других фиксированных товаров (N вагонов), например телефоны и аксессуары к ним;

• товары-магниты: товары, рост продаж которых влечёт рост продаж многих других товаров; за ними приходят в магазин, и часто они являются первыми товарами в корзине;

• корзинообразующие товары: товары, которые с большой вероятностью, кладут в корзину первыми;

• распространённый товар: товар, который есть во многих магазинах;

• высококонкурентный товар: у этого товара много аналогов в вашем магазине или в других магазинах;

• товары-для-всех: товары, которые купят более 30% пользователей, если дать скидку 50%

• товары с ограниченным потенциалом роста: товары, при увеличении скидки на которые продажи растут с какого-то момента не так сильно, или даже перестают расти и выходят на константу;

Эти специфические термины позволяют инженерам и маркетологам лучше понимать друг друга, маркетологам более формально ставить задачи, а инженерам воплощать "хотелки" маркетологов в конкретные классификаторы и формулы для ранжирования товаров. То есть, буквально, инженеры могут обучать прогнозаторы типа

• E(r);

• вероятность того, что E(0.7) > 10;

• степень N "паровозности товара";

• степень "магнитности товара";

• вероятность того, что пользователь сравнит цену на этот товар с ценой в соседнем магазине;

• какая доля пользователей купит этот товар, если случайному пользователю предлагать на главной витрине скидку 50%.

и потом использовать эти прогнозаторы для отбора и ранжирования товаров.

Задача для примера: как, имея эти прогнозаторы, отобрать топ kvi-товаров?

KVI-товары – это товары, которые влияют на восприятие покупателем цен магазина (price perception). Если попросить маркетолога разложить это на базовые компоненты, то получатся, например, такие пункты:

• это высокоэластичные товары;

• это корзинообразующие товары;

• это товары-магниты;

• это распространённые товары, цену на которые часто сравнивают между магазинами;

• это регулярно покупаемые товары.

И соответственно инженер, имея под рукой 5 соответствующих прогнозаторов, может "сварганить" меру kvi-ности товара.

Другой пример – это товары-герои. Их можно было бы определить как:

• товары-для-всех

• с высокой "магнитностью"

• и E(0.7) > 30

Товары-герои – это то, что логично брать для больших промо акции с медийной поддержкой и для главных витрин в ваших магазинах.

Таким образом, если у вас есть набор базовых прогнозаторов, то списки товаров для той или иной промоактивности на уровне витрин или ценообразования вы можете получать с помощью "алхимии" из базовых прогнозаторов с участием маркетолога и инженера.

Обучение кривой спроса

Меры kvi-ности или геройности товара – это конечно, важно и интересно, но базовая вещь в ценообразовании – это кривая спроса E(r) и именно её нужно обучить в первую очередь.

Возможно, кому-то сама концепция "обучения кривой спроса" звучит непонятно. Как можно обучить кривую спроса? Её можно просто узнать, задав разные цены для одного и того же товара в разные периоды.

На это хочется сказать следующее:

• Явно узнать кривые спроса для товаров, попробовав разные цены, на практике невозможно; на это не хватит времени, и не будет таких периодов стабильности, чтобы можно было сравнивать продажи неделя к неделе. Необходимо как-то извлекать/обобщать информацию из естественных движений цен и продаж в прошлом.

• В прошлом цена менялась и из этих исторических данных можно попытаться извлечь сигнал об эластичности. Хотя можно и случайно "шевелить" цены , чтобы получать информацию о продажах при разных ценах. Это "случайное шевеление" называется exploration. Мы это не делали, и похоже, что в нашем случае естественных исторических данных достаточно, чтобы получить приемлемый результат.

• Товары похожи друг на друга по разным аспектам (аналоги, одна категория, одна ценовая категория, популярность) и поэтому, даже если цена на некий товар X не менялась, или менялась мало, или только в одну сторону, то есть надежда, что есть похожие товары и от них можно "унаследовать" кривые спроса. Есть принципиальная возможность использовать исторические данные по разным похожим товарам для взаимного обогащения и выводить в итоге формулу кривой спроса для любого товара по его свойствам

• Хорошая новость такая – сегодня есть достаточно развитая и продолжающая активно развиваться область компьютерных наук – Machine Learning, в которой есть готовые решения – алгоритмы и технологии – позволяющие по историческим данным получать ответы. По сути ML предоставляет набор инструментов, который позволяет, в частности, автоматизировать задачу получения кривой спроса для товара по его свойствам, и "одним махом" решается задача определения близости товаров друг другу и то, как разным товарам, близким по тому или иному аспекту, правильно "наследовать" полезную историческую информацию о том, к какому росту продаж привела та или иная скидка.

По сути инженер ML может сделать такую "чёрную коробку", в которую можно отправить данные вида

Поле чего она обучится – научится решать задачу прогнозирования столбца sales (число продаж). А именно, ей на вход можно будет подавать аналогичную таблицу, но без столбца "sales", и она сама дорисует этот столбец прогнозными значениями. Можно взять одну строчку из такой таблицы и попробовать подставить в столбец price самые разные значения и в итоге получить разные значения sales. Это и будет прогнозируемая кривая спроса. Важную роль играют факторы (features) – это несколько столбцов с разнообразной информацией о товаре (категория товара, среднее число продаж за последний месяц, цена у конкурента в этот день) и дне (день недели, праздник, период распродаж и др.).

Факторы – это и есть ключ к задаче, именно в факторах ищутся закономерности и какие-то обобщения – как та или иная комбинация факторов влияет на спроса. Цена – это тоже фактор, но особенный, так как мы его рассматриваем как переменную величину и во время прогноза задаём руками.

Сложности в задаче обучения кривой

В задаче обучения кривой спроса есть ряд сложных моментов, методы преодоления которых выходят за рамки этой статьи. Например, такие

• Для промоакций и цены разные эластичности. Вообще для каждой промомеханики (скидка, промокод, купон) может быть своя кривая, а точнее не для промомеханики, а для комбинации факторов связанных с маркетингом и не только (см. выше "Факторы, влияющие на эластичность" – видимость, ожидаемость, понятность).

• Если скидки сопровождаются какой-то дополнительной промоактивностью (реклама в телевизоре, на сайте, на витрине магазина, пушами в приложении), то эластичность во многом определяется качеством и проработкой этой промоактивности.

• Long-term vs short term кривые могут отличаться. То есть изменение цены может повлиять на продажи, но не сегодня и завтра, а через пару месяцев.

Учёт этих моментов, видимо, не простая задача.

Подготовка данных для обучения

Чистим данные

Тут всё как всегда – нужно тщательно готовить данные, перепроверяя разумность и чистоту данных, выкидывать опасные "сэмплы". А именно, полезно убрать из обучающих данных (train dataset) строчки, которые затрагивают

• OOS (out of stock);

• распродажи остатков товара;

• мертвые сезоны (шубы летом);

• и вообще, нужно выкидывать любые выбросов на графике продаж конкретного товара – странные отклонений как вверх, так и вниз.

Сезонность

Следующий сложный момент – сезонность. Изменение продаж иногда связано с сезонностью и хотелось бы, чтобы ML не приписывал к цене для случаев, когда вход, выход из сезона совпал с изменением цены.

Здесь есть подход основанный на добавлении факторов про сезон на уровне категорий товаров, но вполне рабочий. Учёт сезонности, похоже сложная задача, и не смотря на то, что она невооружённым глазом видна на уровне категорий, на уровне товаров она не работает – товар, который в сезон выстрелил в прошлом году не выстрелит в этом, его место займет аналог. Сезонные множители сильно разняться между товарами одной категории и не повторяются год от года. Но для задачи обучения нормализованной кривой спроса, оказывается, сезонность не так важна. Как дальше станет понятно, оптимальная цена определяется именно нормализованной кривой спроса, и абсолюты продаж не так важны. Она из простых идей добавить учёт сезонности в обучения – это просто добавить фактор про день года, но при этом полезно проконтролировать, что этот фактор не приводит к переобучению (overfitting). Проверка может заключаться в добавлении специальной регуляризации этого фактора методом его зашумления при обучении или уменьшением числа слоёв в специальной "короткой ноге нейросетки", в которую на вход подаются такие опасные факторы. Но об этом речь ещё впереди.

Многофакторные модели

Вообще, разговор про сезонность подводит нас к важному пониманию необходимости многофакторной модели. Нам хотелось бы, чтобы часть движений продаж могла смогла объяснить не движением цены, а чем-то другим, например:

• сезонностью и праздниками;

• изменением погоды;

• действиями конкурентов (reference prices);

• маркетинговой активностью (вашей, или конкурентов).

Поэтому полезно добавлять соответствующие этим явлениям факторы, чтобы они брали на себя объяснение некоторых движений продаж и в результате при факторе price оставалась чистая правильная эластичность по цене. Хотя, честно говоря, мы в Яндекс Маркете погоду как фактор ещё не добавили.

Проблема многих факторов

Объяснение из предыдущего параграфа намекает, что есть и проблема другого сорта. Некоторые факторы могут содержать информацию о цене и тем самым "очистить" эластичность по цене от самой цены. Например, добавив фактор price_yesterday (цена вчера) мы рискуем попасть в ситуацию, что ML часть зависимости продаж от цены price (цена сегодня, в день date) поместит в зависимость от фактора price_yesterday, так как очень часто будет ситуация price_yesterday = price. Это пример понятной явной утечки. Но утечки бывают более сложные, например, если вы в качестве факторов возьмёте вектор продаж последние 14 дней, то тогда есть опасность, что в уменьшении продаж вчера нейросеть заподозрит увеличение цены вчера, и будет права. Ну а дальше опять та же история – если вчера цена была высокой, то и сегодня скорее всего тоже, и поэтому в фактор price можно даже не заглядывать.

Задача регрессии

Давайте выберем какой-либо товар и посмотрим цены и продажи за последние N дней, в итоге на плоскости (log(price), log(sale+1)) можно получить "облако" из N точек.

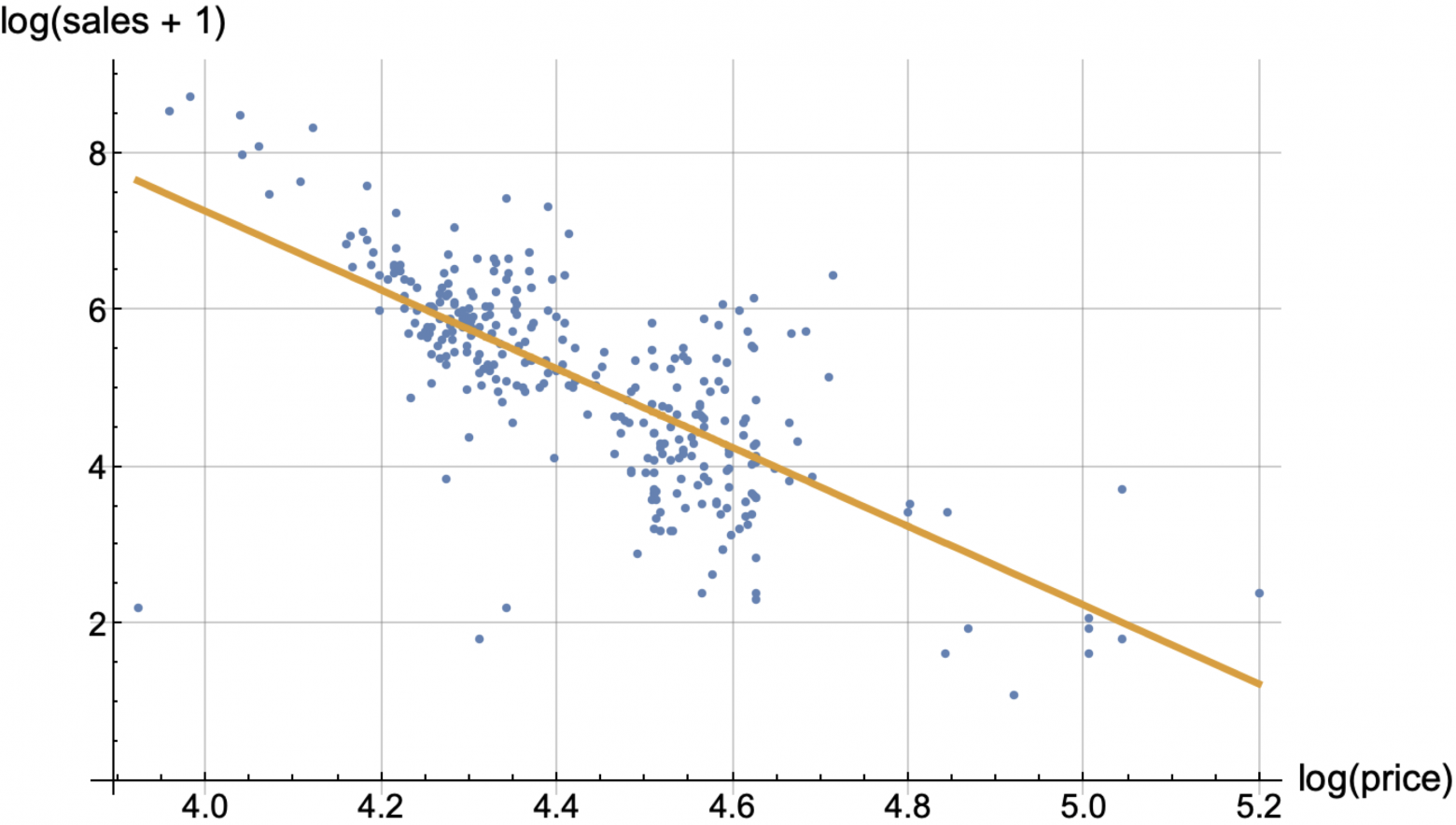
Именно в таких осях у нас живут нейросети и разные регрессионные модели, то есть модели у нас на выходе имеют не sales, а predict = log(sales + 1) и predited_sales вычисляются по формуле max(0, exp(predict) - 1). То, что мы заставляем модели прогнозировать не продажи, а какую-то нелинейную функцию от продаж, мы называем target_transform. Мы попробовали самые разные варианты target_transform и остановились на этом.

Мотом можно попробовать провести прямую линию через это облако точек, решая стандартную регрессионую задачу уменьшения суммы квадратов отклонений точек от прямой. И этот вариант уже дает более менее приемлемое решение.

Но в этом варианте особенно важно проделать то, что выше я обозначил как "чистку данных" (от OOS, мертвых сезонов, распродаж дедстока и др.).

Следующий важный шаг – это проводить не прямую, а например, сумму sigmoid-функций (перевернутых), чтобы находить точки скачков продаж – точки, связанные либо с психологическими границами, либо с ценами конкурентов.

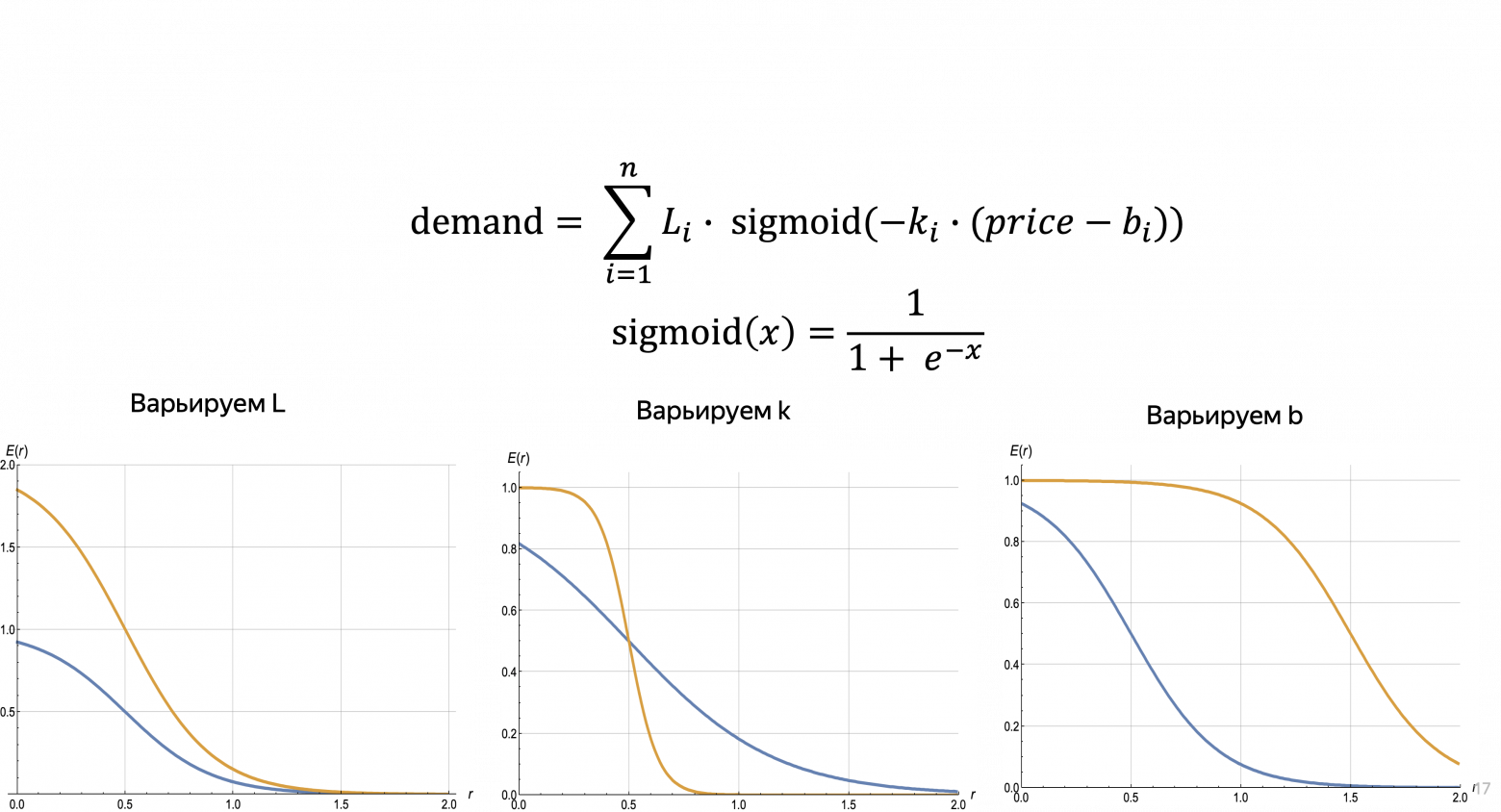
В итоге такой параметризации можно получать прогнозные кривые E(r) такого вида.

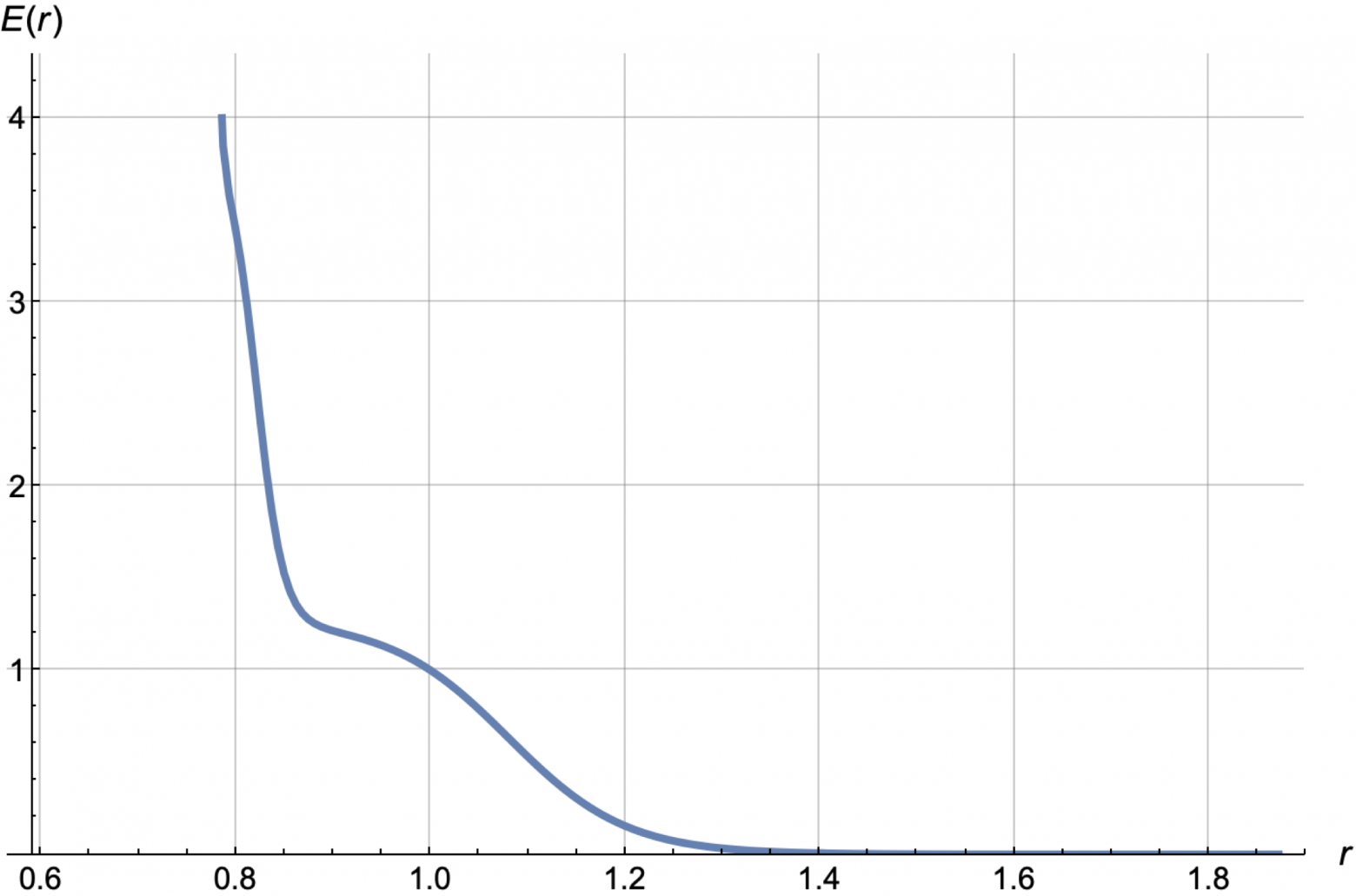
Но замена линейной регрессии на параметрическую – это полшага. Важно, чтобы

• модели могли прогнозировать не только прямые на плоскости (f(price), g(sales));

• модели были многофакторные, чтобы при цене "оседала" очищенная эластичность.

Факторы

Вот наш список факторов.

• Фичи продаж и цен за последние N дней

• Корреляции продаж и цен за последние N дней

• Цены конкурентов

• Эмбеддинги товара, категорий товаров

• Информация о промо (если была какая-то дополнительная к скидке промоактивность)

• Сезонность

• Время доставки

Тут интересны факторы "Корреляции продаж и цен за последние N дней". Пусть у вас есть средняя цена в день и продажи в день для последних 42 дней. Тогда вы можете вычислять

для разных u и v. Каждая пара u и v даёт фактор. Здесь можно брать какие-либо другие нелинейные функции от sales и price, например, логарифмы.

Подготовка факторов и их нормализация для нейросетей – особое искусство, от которого сильно зависит качество результата. Мой персональный "алхимический набор" такой:

• По возможности все факторы делать безразмерными, например:

  • вместо avg_d28_price – средняя цена за n=28 дней – я добавляю avg_d28_price_norm = log(avg_d28_price / price₀);

  • вместо avg_d28_sales – средние продажи за 28 дней – я добавляю avg_d28_sale_norm = log(avg_d28_sales / demand₀).

• Если и добавляю фактор с размерностью (руб. или штуки продаж), то логарифмирую его.

• Если какой-то фактор можно очистить от странностей, то нужно это сделать, например, средние продажи по 42 дням можно сделать средними продажами за 42 дня по "чистым" дням, где чистые дни – это дни без распродаж и без OOS.

• Если очистка какого-то фактора выглядит сложной, то нужно дать необходимые данные в виде факторов, чтобы нейросеть сама смогла сделать очистку; например, можно дать вектор данных о продажах в день за последние 14 дней, а также вектор с информацией был ли товар но стоке для каждого из этих 14 дней. Но как я писал выше давать данные о продажах в предыдущие дни опасно, так как через них протекает сигнал об изменении цены, поэтому в нашем случае полезно делать чистку руками.

Фильтрация периодов стабильности

Следующий важный шаг, который был проделан – это выкидывание из train dataset 98% случайных строк, в которых цена слабо (менее чем на 5%) отличается от средней цены за 42 дня. Этим мы подчёркиваем, что нам важны моменты смены цены, и заставляем модель уделять этому больше внимания, нежели задаче прогнозирования спроса в дни стабильной цены.

Архитектура нейросети

Если говорить коротко и по существу, то у нас лучше всего отработала нейросетевая модель, в которой

• глубина равна 9, средний размер внутреннних слоев равен 15;

• число факторов на входе равно ~70;

• transformed_target = log(sales +1);

• размер train_dataset от 4 млн до 20 млн (мы делали модели для разных ассортиментов – брали все товары, или избранное подмножество);

• сделана нормализация факторов на входе (каждый фактор отнормирован так, что его среднее равно 0, а дисперсия на train dataset равна 1);

• есть один residual connection;

• есть парочка LayerNorm.

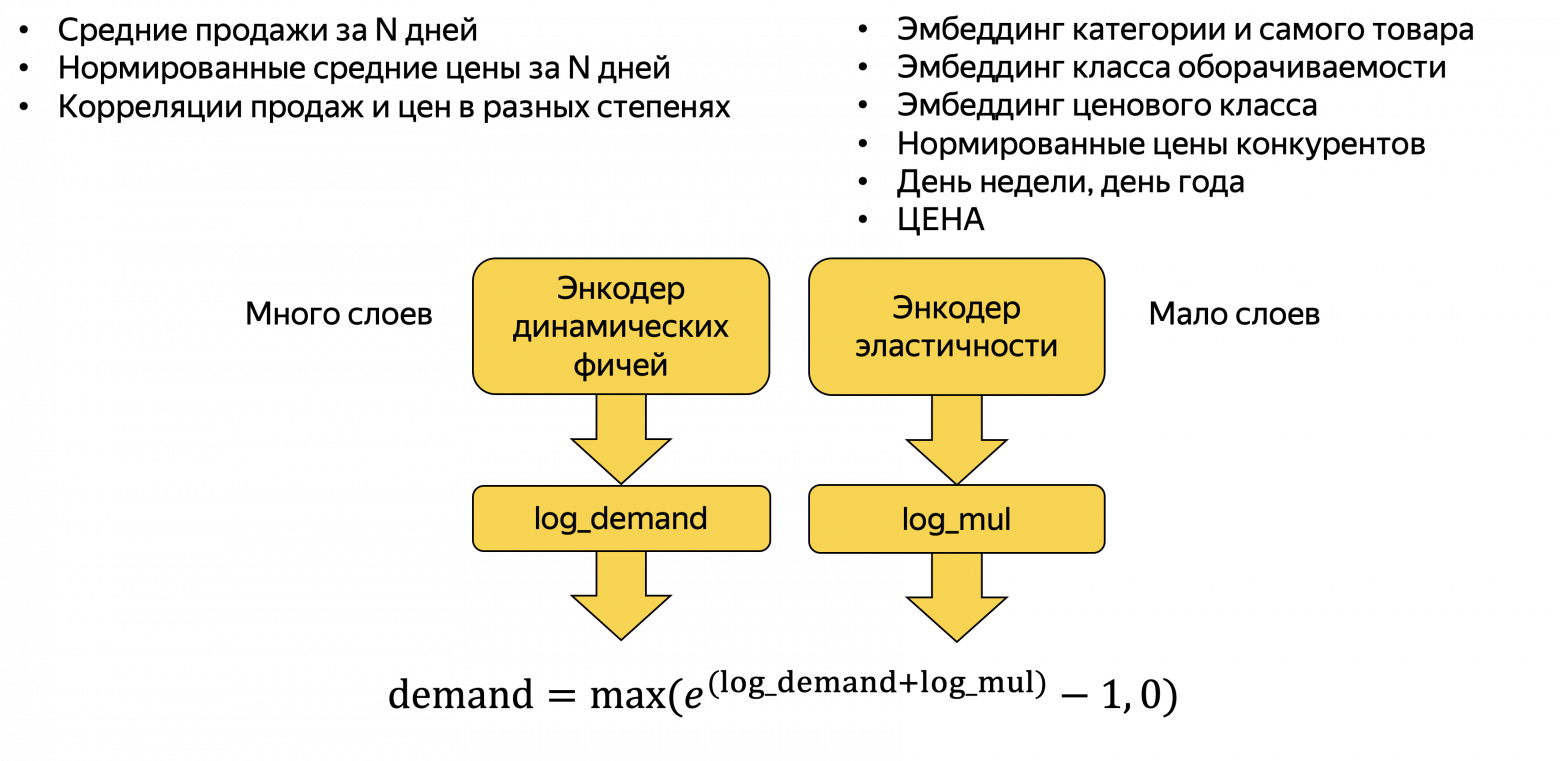
"Левая нога" (энкодер динамических фичей) имеет примерно такой код (class DemandNet1):

import torch
import torch.nn as nn

class DatasetNormalization(nn.Module):
    """
        Just add this layer to normalize you raw features
        (but do not forget to take log of counters-like features by yourself, using features_transforms)
    """
    def __init__(self, x, nonorm_suffix_size=0):
        super().__init__()
        mu = torch.mean(x, dim=(-2,))
        std = torch.clamp(torch.std(x, dim=(-2,)), min=0.001)
        if nonorm_suffix_size > 0:
            mu = torch.cat((mu, torch.zeros(nonorm_suffix_size)))
            std = torch.cat((std, torch.ones(nonorm_suffix_size)))
        self.p_mu = nn.Parameter(mu, requires_grad=False)
        self.p_std = nn.Parameter(std, requires_grad=False)

    def forward(self, x):
        # ParameterList can act as an iterable, or be indexed using ints
        return (x - self.p_mu) / self.p_std
      
class DemandNet1(nn.Module):
    """
    This network is the first to try.
    + DatasetNormalization
    + Some Linear + ReLU, one LayerNorm inside
    + one residual connection
    """
    __constants__ = ['output_size']

    def __init__(
        self, 
        x_norm_prefix, # часть или весь train_dataset без embeddings,
                       #  чтобы вычислить DatasetNormlization layer
        mid_size: int = 5,
        embed_size: int = 0,
        output_size: int = 1,
        activation: nn.Module = nn.ReLU()
    ):
        super().__init__()
        input_size = len(x_norm_prefix[0]) + embed_size
        self.norm = DatasetNormalization(x_norm_prefix, embed_size)
        self.output_size = output_size
        self.leg = nn.Sequential(
            nn.Linear(input_size, mid_size),
            activation,
            nn.Linear(mid_size, mid_size),
            nn.LayerNorm(mid_size),
            activation,
            nn.Linear(mid_size, mid_size),
            activation,
            nn.LayerNorm(mid_size)
        )
        self.body = nn.Sequential(
            nn.Linear(input_size + mid_size, mid_size),
            activation,
            nn.Linear(mid_size, mid_size),
            activation,
            nn.Linear(mid_size, output_size)
        )

    def forward(self, x):
        x1 = self.norm(x)
        x2 = self.leg(x1)
        x = torch.cat((x1, 4 * x2), dim=1)
        yp = self.body(x)
        return torch.squeeze(yp) if self.output_size == 1 else yp

Правая нога – это более сложная штука и её я приводить не буду. В принципе, вы можете использовать одноногую архитектуру (вся сетка DemandNet1 как одна нога и в неё отправить все факторы) – это даёт результат не сильно хуже по метрикам.

Иногда хочется прогнозировать не продажи в один день (завтра или через K дней), а вектор продаж (продажи через K дней, через K + 1 день, через через K + 2 день, ...). Соответственно есть возможность делать тензорный таргет лишь бы ваш Loss это поддерживал.

Также на вход нейросетке я подавал эмбединги категориальных факторов. Не вдаваясь в подробности, перечислю их имена: sku, sku_category, sku_level_1_category, normalized_sku_name, price_class, demand_class. Каждый из этих 6 идентификаторов "эмбедился" в пространство малой размерности (2, 3, 4 или 5) и они в сумме давали дополнительные embed_size = 20 факторов.

В качестве loss-функции для transformed_target можно брать обычный MSELoss, но еще неплохо работает слегка модифицированный SmoothL1Loss с параметрами qx=0.65 и beta=1.0 – это квантильный лосс для 65% квантили со сглаженной вершинкой:

import torch.nn as nn
import torch.nn.functional as F

class SmoothQLoss(nn.L1Loss):
    __constants__ = ['reduction', 'beta', 'qx']

    def __str__(self):
        return f"{self.__class__.__name__}(beta={self.beta}, qx={self.qx})"

    def __init__(
        self,
        size_average=None,
        reduce=None,
        reduction: str = 'mean',
        qx: float = 0.5,
        beta: float = 0.1,
    ) -> None:
        super().__init__(size_average, reduce, reduction)
        self.beta = beta
        self.qx = qx

    def forward(self, predict: torch.Tensor, target: torch.Tensor) -> torch.Tensor:
        m = 2.0 * self.qx - 1.0
        shift = self.beta * m
        if self.reduction == 'mean':
            return (
                F.smooth_l1_loss(target - shift, predict, reduction=self.reduction, 
                                 beta=self.beta)
                + m * torch.mean(target - predict - 0.5 * shift)
            )
        elif self.reduction == 'sum':
            return (
                F.smooth_l1_loss(target - shift, predict, reduction=self.reduction, 
                                 beta=self.beta)
                + m * torch.sum(target - predict - 0.5 * shift)
            )

Метрики качества прогноза кривой спроса

Во время экспериментов с факторами и архитектурой сети важно иметь простую offline-метрику, которая позволяет быстро решать, хорошее было изменение или нет. В конечном итоге мы пришли к метрике, которая в Catboost известна как QueryRMSE.

В качестве группы (query_id) мы взяли пару group = (категория товара, ценовая категория товара), а в качестве таргета – y = log(sales+ 1).

Идея заключается в том, что для каждой группы ищется аддитивная поправка , которая минимизирует средний квадрат отклонения (mean square error, MSE) между y_true = log(fact_sales+ 1) и y_predicted = log(predicted_sales+ 1) :

а потом полученные значения ошибок в группах усредняются, возможно, с некоторыми весами:

Эта метрика, в отличие от обычной метрики ошибки mse, меньше думает об ошибке в абсолютах, и больше – про ошибки в нормализованной кривой спроса. Метрика corr_mse буквально прощает аддитивные ошибки в группах.

Но аддитивные ошибки для y = log(sales + 1) – это, грубо говоря, мультипликативные ошибки в прогнозе самих sales. То есть, если мы в своем прогнозе для всех товаров в группе ошибемся в 2 раза, метрика нам это простит и не зачтёт как ошибку. Ей важно, чтобы мы правильно прогнозировали отношения продаж для товаров из одной группы.

ML пайплан

Важные слова, которые нельзя не сказать. Залогом успеха ML исследований и внедрения ML в работающую систему всегда является полный пайплайн, который позволяет собрать все необходимые данные, сформировать train dataset и test dataset, обучить несколько вариантов моделей на train dataset, сделать для них прогноз на test dataset, вычислить метрики и сформировать таблицу с этими результатами. Важно, чтобы этот пайплайн был

• от исходных данных до таблицы победителей сортированной по одной метрике (чтобы не спорить, какая модель лучше);

• воспроизводимый (иначе нет веры);

• быстро работающий (от идеи до проверки результата день или меньше);

• без багов (это, конечно, вряд ли, но помечтаем);

• с отдельной кнопкой для запуска "в прод" и кнопкой для "отката".

Использование кривой спроса

Задача максимизации прибыли

Когда у вас есть кривая спроса, вы можете явно решить задачу максимизации прибыли. Давайте упрощённо, упуская некоторые моменты налогообложения, запишем формулу для прибыли:

Здесь были введены дополнительные обозначения:

Сам cost – это закупочная цена + операционные расходы + ещё что-то – не так важно, что. Максимально точное общее определение для наших целей такое:

cost – это то, то надо вычитать из цены, чтобы получить нечто пропорциональное прибыли.

Введём функцию относительной прибыли :

Задача максимизации прибыли по сути сводится к поиску цены r, которая максимизирует P(r).

Рассмотрим пример.

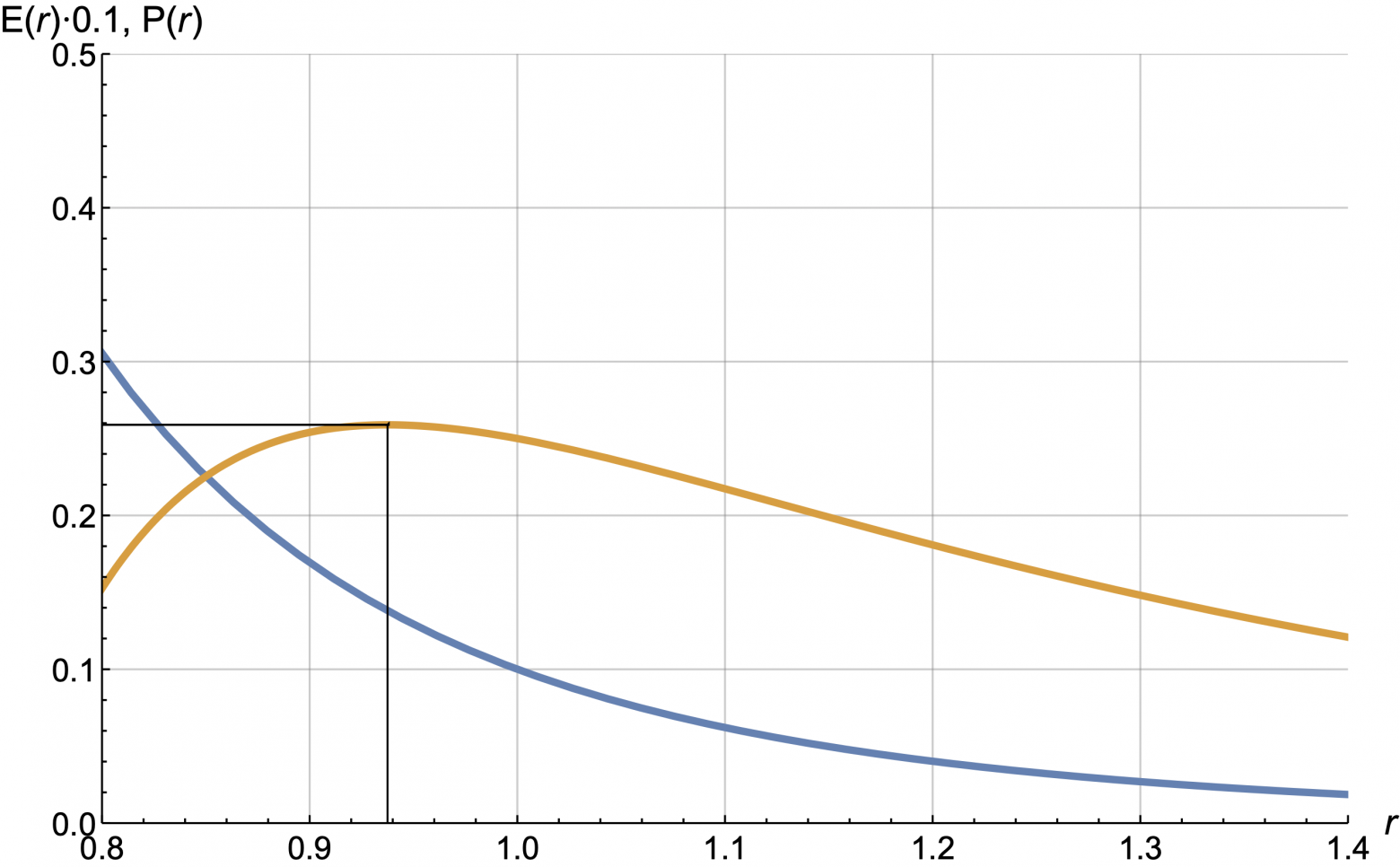
График прибыли (желтый) имеет максимум где-то в окрестности числа 0.94, то есть для максимизации прибыли цену price₀ надо уменьшить на 6%. Для степенной кривой E(r) максимум прибыли достигается для цены

Я дальше выпишу формульные ответы для этой задачи для других кривых как частный случай другой, более общей задачи.

Задача баланса оборот vs прибыль

Задача Яндекс Маркета – это не задача максимизации прибыли. Нам важны продажи и адекватность цен. Если сильно огрубить ситуацию, то задача близка к задаче балансировки между двумя метриками – оборотом и прибылью.

А когда речь идёт о балансе, то неизбежно появляется метод множителей Лагранжа.

Метод множителей Лагранжа в примненении к нашему случаю выглядит так:

• Задача 1: Максимизируй при условии, что

при некоторых условиях может быть заменена на

• Задача 2: Максимизируй с некоторым .

Суть в том, что для каждого положительного решение второй задачи даёт ответ на первую задачу для какого-то . Надо просто угадать , чтобы попасть в нужное. Не всегда это удаётся. Здесь отметим, что сам Лагранж проработал случай ограничений типа равенства, то есть, в нашем случае, условий вида, и по факту на практике для нормальных кривых мы достигаем именно равенства. Случай условий в виде нестрогих неравенств был проработан другими математиками, см. условия Каруша — Куна — Таккера.

Интерпретация λ

У числа λ есть простая интерпретация. Каждое λ даёт точку на плоскости (оборот, прибыль). Эти точки вместе образуют синюю кривую на графике ниже.

Желтая прямая – это касательная к синей кривой в точке, в которой мы оказались.

Вам нужно просто угадать такое значение λ, чтобы касательная прямая с такой силой наклона как раз касалась точки с нужным вам значением прибыли.

Есть альтернативная, более правильная школы мысли, когда первично значение λ, а не ограничения на прибыль. Попробую вас в этом сейчас убедить. Когда вы каждый день целитесь в какую-то прибыль, у вас каждый день получается какая-то своя λ. Но меняющееся λ – это плохо. Почему? Аналогия такая. Пусть вы покупаете на рынке помидоры каждый день, и продавцы там так устроены так, что чем больше покупаешь у них помидоры, тем больше цену они назначают. Каждый следующий помидор чуть дороже чем предыдущий. Именно поэтому на рынок нужно ходить каждый день, так как утром цены поменьше, а потом растут. Помидоры не тухнут, и можно было бы один раз закупиться надолго, но, к сожалению, цена для большой партии в один день высокая. Если вы вчера в итоге купили последний помидор по цене 10 руб., а сегодня по 15 руб., то вы поступили неэффективно, так как вчера можно было купить еще парочку по цене чуть больше 10, а сегодня последние помидоры по 15 руб. не покупать. Значение λ – это и есть цена последнего помидора. А помидор – это 1 рубль прибыли, который вы покупаете за λ рублей оборота.

Конечно, бизнесу проще думать про конкретное значение прибыли и про кеш, который им важно иметь каждый месяц, чтобы покрыть уже запланированные расходы. Но оптимальное решение заключается в том, чтобы волшебным образом угадать λ и не менять его длительное время или лишь слегка "подруливать", типа раз в неделю λ = 7.4 менять на λ = 7.2. Можно брать λ с запасом, а избытки прибыли уметь оперативно тратить с хорошим разменом на оборот в каких-то промо акциях.

Ответы от Лагранжа

Рассмотрим три семейства кривых.

Ответы "от Лагранжа" для них выглядят следующим образом:

Оптимальные значения r обозначены на следующих картинках пунктирными линиями

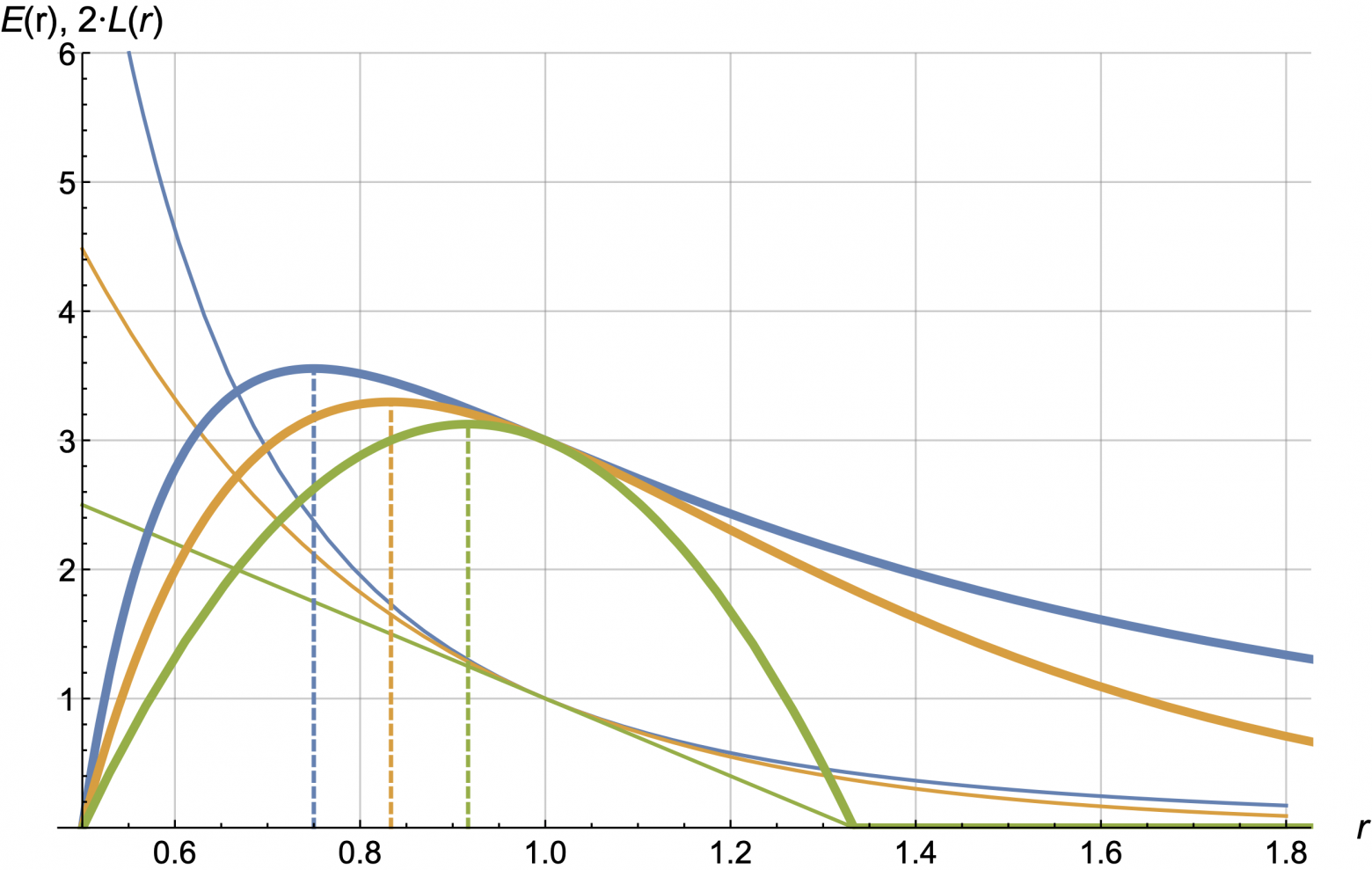
Обсудим первый (синий) вариант как самый типичный.

Когда нужно ставить цену в точности равную c. И на продажах этого товара мы не будем ничего зарабатывать, но и терять тоже не будем. Если же , то цена будет меньше c, и на этом товаре мы будем терять прибыль (и это нормально и правильно), а на товарах с мы будем зарабатывать.

Когда эластичность мала и приближается к 1, формула говорит ставить сколь угодно большую цену. Это связано с тем, что степенная кривая не совсем правильно описывает область высоких наценок и это надо учитывать при использовании этой формулы. Простейший вариант исправления этой неприятности, это

• добавление в E(r) экспоненциального затухания продаж с некоторой наценки;

• и поиск максимума L численным образом.

Алгоритм

Здесь важно то, что задача решается не отдельно для каждого товара, а для совокупности. Ограничение П₀ – это ограничение на суммарную прибыль по всем товарам.

В этой формуле все величины gmv₀, r, E(r) и c свои для каждого sku.

Если прибыль покажется вам маленькой, увеличьте λ до 5. Если всё ещё мало, то увеличивайте до 10. Если прибыль вам понравиться, то дальше вы можете постепенно уменьшать λ чтобы растить продажи и завоёвывать рынок.

Шаги 2 и 3 на самом деле можно не зацикливать, а просто, прострелять сотню вариантов и выбрать понравившееся значение по метрикам оборот и прибыль. Но я намеренно обозначил здесь цикл, имея в виду, что процесс должен быть реализован через реальное выставление цен на практике и регулярное подруливание в направлении необходимого результата. Нужно постоянно искать разрезы, где модель ошибается, исправлять эти ошибки, и снова проверять на реальных продажах и так далее.

Takeaways

• Обучение кривых спроса:

  • Тщательная подготовка данных (иначе garbage in – garbage out).

  • Многофакторность (чтобы другие факторы забирали на себя часть объяснений изменения числа продаж).

  • Отработанный ML пайплайн (чтобы проверить сотни вариантов моделей и отобрать лучшую).

  • Нейросети предоставляют сейчас хороший инструментарий, чтобы опытный ML-алхимик получил приемлемые результаты и обошёл множество подводных камней.

• Оптимальная цена:

  • Лагранж "рулит" для экономических задач про баланс нескольких KPI.

  • Одна из рабочих формул оптимальной цены:
    
    

• Успех мероприятия = ML + Аналитика + Экспертные знания.

  • ML-инженеры могут обучить E(r).

  • Эксперты – указать как влиять на E(r), указать на некоторые странности в результатах и помочь улучшить модель, устранив эти странности, обозначить области применимости формул.

  • Аналитики – делать честные оценки алгоритмов ценообразования, находить ошибки и делать правильные выводы.