Объявляю пятиминутку без разговоров о некомпьютерных вирусах на IT-сайте! А ведь без шуток. Если вы говорите по-французски или живёте во Франции, то вы можете участвовать в конкурсе, который я организую в нашем НИИ в рамках конференции jFIG2020 (французские дни компьютерной графики). Но даже если вы не можете участвовать, читайте про рейтрейсинг на пальцах. Моя основная задача — нести свет культуры компьютерной графики в ширнармассы!
Итак, как сделан этот шейдер, который анонсирует сам конкурс?
Если вдруг вы его не узнали, то это воксель-арт версия стэнфордского кролика:

Год назад я уже написал пару статей о том, насколько просто рисовать всякие картинки:
Общий принцип
До сих пор я много рассказывал об общих принципах компьютерной графики, но практически всегда показывал примеры на голом цпп. На сей раз будем греть планету не при помощи центрального процессора, но графической карты! Кстати, я не шучу, это мой первый шейдер на shadertoy, так что не стесняйтесь меня поправлять.
Итак, общий принцип рейтрейсинга крайне примитивен. Мы берём камеру, перед ней определяем сетку пикселей (наш экран), через каждый пиксель испускаем луч, и смотрим, где именно он пересекается с нашей сценой, что даёт нам цвет текущего пикселя. Вот иллюстрация:
А вот главный кусок кода рейтрейсинга: мы просто проходимся по всем пикселям и в итоговый фреймбуфер пишем получившийся цвет. Обратите внимание на #pragma omp parallel for! Вычисления для всех пикселей абсолютно независимы друг от друга.
vec3 origin = [...];
#pragma omp parallel for
for (size_t j = 0; j<height; j++) {
for (size_t i = 0; i<width; i++) {
vec3 direction = [...];
framebuffer[i+j*width] = cast_ray(origin, direction);
}
}Этап первый: заливаем картинку градиентом
Давайте попробуем то же самое сделать на графической карте. Моя задача на данный момент суметь залить картинку градиентом, чисто для того, чтобы убедиться, что я могу контролировать вывод на экран. Вот что должно получиться:

А вот так выглядит код, который позволяет добиться нужного нам эффекта. Посмотреть и запустить код этого этапа можно по этой ссылке.
void mainImage( out vec4 fragColor, in vec2 fragCoord ) {
vec2 uv = fragCoord/iResolution.xy;
vec3 col = vec3(uv.x, uv.y, 0.);
fragColor = vec4(col, 1.);
}Основная разница с предыдущим кодом в том, что тут нет двойного цикла по всем пикселям картинки, это за нас делает сама графическая карта. Функция mainImage вызывается для каждого пикселя картинки, она на вход получает координаты пикселя fragCoord и на выход должна дать его цвет fragColor. Просто, правда? Посмотрите, каких эффектов могут добиться монстры:
На такие высоты я, конечно, не целюсь, моя задача научить основам (здорово я вывернулся, да? типа, я бы мог, да вот только недосуг!). Вышеприведённый код — это фрагментный шейдер. Разумеется, существуют и другие типы шейдеров, но это не входит в тему сегодняшнего разговора.
Этап второй: рисуем название конференции
Теперь я хочу поверх всего написать название конференции, должно выглядеть вот так:

Посмотреть и запустить код этого этапа можно непосредственно на shadertoy.
Как это работает? Очень просто! Представьте себе, что у нас есть двумерный массив булевских значений bool jfig[32][18]. Разобьём нашу картинку на сетку 32x18 квадратиков, и осветлим те, что соотвутствуют значению true в массиве jfig:
void mainImage( out vec4 fragColor, in vec2 fragCoord ) {
vec2 uv = fragCoord/iResolution.xy;
vec3 col = vec3(uv.x, uv.y, 0.);
vec2 coord = fragCoord/iResolution.xy*vec2(32, 18);
if (jfig(uint(coord.x), uint(coord.y))) {
col += vec3(.5);
}
fragColor = vec4(col, 1.);
}Разумеется, хранить напрямую 32*18 массив булевских значений я не хочу, т.к. bool в языке glsl занимает… 32 бита! Поэтому я храню бинарную картинку в битовом поле jfig_bitfield и функция bool jfig(in uint x, in uint y) выковыривает нужный бит путём нехитрых манипуляций с битовым полем:
#define JFIGW 32u
#define JFIGH 18u
uint[] jfig_bitfield = uint[]( 0x0u,0x0u,0x0u,0xf97800u,0x90900u,0xc91800u,0x890900u,0xf90900u,0x180u,0x0u,0x30e30e0u,0x4904900u,0x49e49e0u,0x4824820u,0x31e31e0u,0x0u,0x0u,0x0u );
bool jfig(in uint x, in uint y) {
uint id = x + (JFIGH-1u-y)*JFIGW;
if (id>=JFIGW*JFIGH) return false;
return 0u != (jfig_bitfield[id/32u] & (1u << (id&31u)));
}Этап третий, самый важный: добавляем фон
В итоге у нас должна получиться вот такая картинка:

Посмотреть и запустить код этого этапа можно непосредственно на shadertoy. Этот этап я назвал самым важным, поскольку именно здесь мы проделаем основную работу по рейтрейсингу. Ведь фоновая картинка у нас не просто плоская, а самая настоящая кубическая текстура.
Вот так выглядит наш код:
struct Ray {
vec3 origin;
vec3 dir;
};
vec3 cast_ray(in Ray ray) {
return texture(iChannel0, ray.dir).xyz;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord ) {
const float fov = 3.1416 / 4.;
vec2 uv = (fragCoord/iResolution.xy*2. - 1.)*tan(fov/2.);
uv.x *= iResolution.x/iResolution.y;
vec3 orig = vec3(0., 0., 1.);
vec3 dir = normalize(vec3(uv, -1));
vec3 col = cast_ray(Ray(orig, dir));
fragColor = vec4(col, 1.);
}Самое сложное в этом коде — это первые пять строчек после объявления функции mainImage. Что там происходит? Давайте разбираться. Предположим, камера у меня находится в начале координат, и при этом направлена вдоль оси -z. Давайте я это проиллюстрирую вот такой картинкой, она показывает камеру сверху, ось y торчит прямо из монитора:
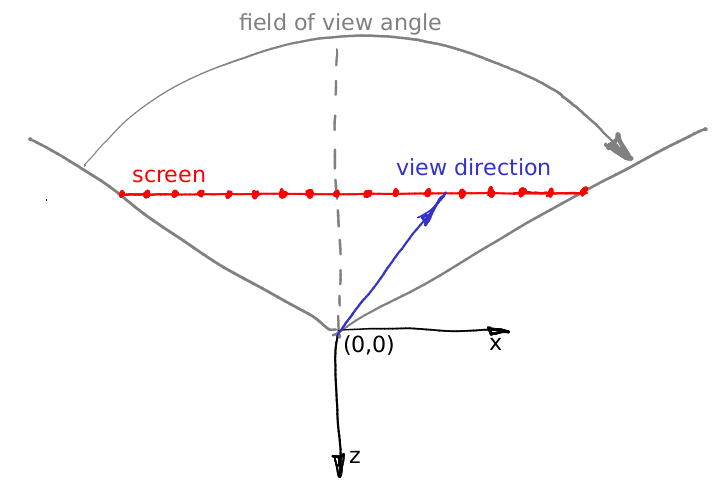
Экран у меня лежит на плоскости с уравнением z=-1. Угол обзора (константа) задаёт сектор, который будет будет виден на экране. На этой картинке у меня экран шириной 16 пикселей, как мы можем посчитать его длину в мировых координатах? Очень просто. Давайте рассмотрим треугольник, образованный красной, серой и пунктирной серой линиями. Легко видеть, что tan(fov/2) = (screen width) * 0.5 / (screen - camera distance). Мы поместили экран на расстоянии одного метра от камеры, таким образом, (screen width) = 2 * tan (fov/2).
А теперь давайте представим, что мы хотим пропустить луч из камеры через 12й пиксель на экране, то есть, мы хотим посчитать синий вектор. Как это сделать? Каково расстояние от левого угла экрана до конца вектора? Начнём с того, что это 12+0.5 пикселей. Мы знаем, что 16 пикселей экрана соответствуют 2*tan(fov/2) метрам. Таким образом, кончик вектора находится на (12+0.5)/16 * 2*tan(fov/2) метров от левого края экрана, ну или на расстоянии (12+0.5) * 2/16 * tan(fov/2) - tan(fov/2) от пересечения экрана с осью -z. Добавьте в это рассуждение соотношение сторон экрана и вы получите строго пять самых сложных строчек моего кода.
В отличие от иллюстрации, у меня в коде камера находится в точке (0,0,1), а экран на плоскости z=0, но это абсолютно не меняет вычислений.
Этап четвёртый: пускаем камеру по кругу
Как и прежде, посмотреть и запустить код этого этапа можно непосредственно на shadertoy. Примерно вот такой результат нам нужен:
Раньше наша камера была фиксирована в точке (0,0,1) и смотрела вдоль оси -z, а теперь она ездит по окружности с единичным радиусом и её взгляд прикован к началу координат. Семь новых строчек кода и коррекция двух строчек старого дают всё что нам нужно:
vec3 rotateCamera(in vec3 orig, in vec3 dir, in vec3 target) {
vec3 zAxis = normalize(orig - target);
vec3 xAxis = normalize(cross(vec3(0., 1., 0.), zAxis));
vec3 yAxis = normalize(cross(zAxis, xAxis));
mat4 transform = mat4(vec4(xAxis, 0.), vec4(yAxis, 0.), vec4(zAxis, 0.), vec4(orig, 1.));
return (transform * vec4(dir, 0.)).xyz;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord ) {
[...]
vec3 orig = vec3(-sin(iTime/4.), 0., cos(iTime/4.));
vec3 dir = normalize(vec3(uv, -1));
dir = rotateCamera(orig, dir, vec3(0.));
[...]
}Этап пятый: рисуем квадратик
Теперь давайте нарисуем квадратик с длиной ребра полметра, живущий на плоскости z=0:

Для этого нам достаточно добавить совсем немного кода в функцию cast_ray():
vec3 cast_ray(in Ray ray) {
if (abs(ray.dir.z)>1e-5) {
float dist = (0. - ray.origin.z) / ray.dir.z;
if (dist > 0.) {
vec3 point = ray.origin + ray.dir*dist;
if (point.x>-.25 && point.x<.25 && point.y>-.25 && point.y<.25) {
return vec3(0.2, 0.7, 0.8);
}
}
}
return texture(iChannel0, ray.dir).xyz;
}Посмотреть и запустить код этого этапа можно непосредственно на shadertoy.
Как это работает? Для начала нам нужно найти точку пересечения луча и плоскости, в которой живёт квадратик (z=0). Я проверяю, не параллелен ли луч плоскости if (abs(ray.dir.z)>1e-5). Уравнение луча выглядит следующим образом: vec3 point = ray.origin + dist*ray.dir, где dist — это расстояние от текущей точки луча до начала, правильно? Нам известна координата z точки пересечения (z=0); тогда расстояние от начала луча до точки пересечения считается как float dist = (0. - ray.origin.z) / ray.dir.z. Ну а дальше дело техники, получив точку пересчения point мы проверяем, укладываются ли координаты x и y в квадрат со стороной полметра с центром в начале координат. Вуаля!
Этап шестой: рисуем куб
Ну раз уж мы умеем нарисовать один квадрат, нам совсем несложно нарисовать шесть квадратов, которые составляют куб! Посмотреть и запустить код этого этапа можно непосредственно на shadertoy.

Вот так выглядит код пересечения произвольного луча с кубом, ориентированным по осям системы координат:
struct Box {
vec3 center;
vec3 halfsize;
};
bool box_ray_intersect(in Box box, in Ray ray, out vec3 point, out vec3 normal) {
for (int d=0; d<3; d++) {
if (abs(ray.dir[d])<1e-5) continue;
float side = (ray.dir[d] > 0. ? -1.0 : 1.0);
float dist = (box.center[d] + side*box.halfsize[d] - ray.origin[d]) / ray.dir[d];
if (dist < 0.) continue;
point = ray.origin + ray.dir*dist;
int i1 = (d+1)%3;
int i2 = (d+2)%3;
if (point[i1]>box.center[i1]-box.halfsize[i1] && point[i1]<box.center[i1]+box.halfsize[i1] &&
point[i2]>box.center[i2]-box.halfsize[i2] && point[i2]<box.center[i2]+box.halfsize[i2]) {
normal = vec3(0);
normal[d] = side;
return true;
}
}
return false;
}Этап седьмой: освещение
А теперь давайте добавим диффузное освещение (flat shading), мы же шейдеры рисуем :)

Посмотреть и запустить код этого этапа можно непосредственно на shadertoy. Вот так выглядит наша функция шейдинга:
struct Light {
vec3 position;
vec3 color;
};
Light[] lights = Light[]( Light(vec3(-15,10,10), vec3(1,1,1)) );
vec3 cast_ray(in Ray ray) {
vec3 p, n;
if (box_ray_intersect(Box(vec3(0.), vec3(.25)), ray, p, n)) {
vec3 diffuse_light = vec3(0.);
for (int i=0; i<lights.length(); i++) {
vec3 light_dir = normalize(lights[i].position - p);
diffuse_light += lights[i].color * max(0., dot(light_dir, n));
}
return vec3(0.2, 0.7, 0.8)*(vec3(.7,.7,.7) + diffuse_light);
}
return texture(iChannel0, ray.dir).xyz;
}Этап восьмой: рисуем кролика
Раз уж мы умеем рисовать один куб, то нарисовать несколько не должно составить труда:

Посмотреть и запустить код этого этапа можно непосредственно на shadertoy. Ровно как и в случае с логотипом (двумерной картинкой), я определяю кролика как трёхмерный массив булевых значений, упакованный в битовое поле:
#define BUNW 6
#define BUNH 6
#define BUND 4
#define BUNVOXSIZE 0.1
uint[] bunny_bitfield = uint[]( 0xc30d0418u, 0x37dff3e0u, 0x7df71e0cu, 0x004183c3u, 0x00000400u );
bool bunny(in int cubeID) {
if (cubeID<0 || cubeID>=BUNW*BUNH*BUND) return false;
return 0u != (bunny_bitfield[cubeID/32] & (1u << (cubeID&31)));
}Если вам не очень наглядны константы типа 0xc30d0418u, то вот так они выглядят в человекочитаемом варианте :)
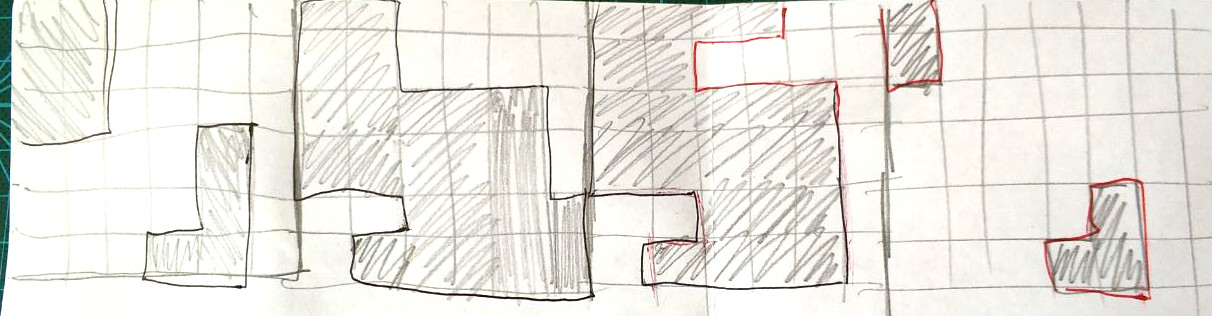
Ну а дальше пишем функцию пересечения луча и вокселизированного кролика:
bool bunny_ray_intersect(in Ray ray, out vec3 point, out vec3 normal) {
float bunny_dist = 1e10;
for (int i=0; i<BUNW; i++) {
for (int j=0; j<BUNH; j++) {
for (int k=0; k<BUND; k++) {
int cellID = i+j*BUNW+k*BUNW*BUNH;
if (!bunny(cellID)) continue;
Box box = Box(vec3(i-BUNW/2,j-BUNH/2,-k+BUND/2)*BUNVOXSIZE+vec3(.5,.5,-.5)*BUNVOXSIZE, vec3(1.,1.,1.)*BUNVOXSIZE*.45);
vec3 p, n;
if (box_ray_intersect(box, ray, p, n) && length(p-ray.origin) < bunny_dist) {
bunny_dist = length(p-ray.origin);
point = p;
normal = n;
}
}
}
}
return bunny_dist < 1e3;
}И в функции cast_ray() заменяем вызов box_ray_intersect() на bunny_ray_intersect(). Вот и кролик!
Этап девятый: раскрашиваем кролика
Ну и самая последняя вещь — это раскрасить кубики в разные цвета. Посмотреть и запустить код этого этапа можно непосредственно на shadertoy.
Тут я велосипед не стал изобретать, и честно стянул чужой код, который для данного целого числа (номер кубика) даёт цвет:

Всё, наш шейдер готов!
Shadertoy.com полон крайне интересных шейдеров, но зачастую понять, как они устроены, могут только эксперты. Если вам интересна эта тема, можете попробовать разобрать мой мультяшный взрыв (кликабельно):

Напоминаю, что если вы говорите по-французски или живёте во Франции, то вы можете претендовать на приз (RTX Quadro) в нашем конкурсе jFIG2020. Правила конкурса будут опубликованы в начале недели, но в целом достаточно мне прислать ссылку на ваш шейдер, а так же на как можно более подробное описание того, как он работает.
Если же вы не живёте во Франции и не говорите по-французски, то хоть на физический приз вы претендовать и не сможете, но вы можете участвовать во всей этой движухе на внеконкурсной основе, нашу нематериальную благодарность и всемирную славу обеспечим :)
Да и вообще пофиг призы, самое главное расцвечивать пиксели!