Поговорим про перформанс-анализ

Когда начинается разговор про перформанс-тестирование, то большинство программистов размышляет только о проведении замеров и сборе метрик, в то время как намного важнее задуматься об анализе собранных значений. Понять, как правильно использовать измеренные метрики и извлечь из них максимум пользы, — не такая уж и простая задача.

Сегодня мы обсудим основные задачи и сложности перформанс-анализа: поговорим о том, как изучать сырые данные и сводные метрики, применять статистические тесты, сравнивать перформансные распределения, писать перформансные тесты, анализировать историю замеров и выбирать правильные метрики. С этим нам поможет Андрей Акиньшин — ниже представлены видеозапись и расшифровка его доклада.

Доклад был сделан летом на нашей .NET-конференции DotNext. Заметим, что 2-5 декабря пройдет новый DotNext, где тему производительности тоже осветят — например, в докладе «Как легко измерить производительность CPU и паттерны аллокации памяти несколькими строками на C#».

Презентацию доклада Андрея можно посмотреть тут.
Далее — повествование от лица спикера.

Задачи перформанс-анализа

Давайте начнём с того, как выглядит типичный день обычного перформанс-инженера.

Порядок действий довольно простой. Нужно взять проблему, изучить её, придумать решение и реализовать его. Потом нужно взять следующую проблему, изучить её, придумать решение и реализовать его. И так от начала трекера и до заката.

Хотя, если подумать, то так выглядит типичный день не только для перформанс-инженеров, но и для многих других инженеров. Так вот, поговорим о том, как выбраться из порочного круга непрерывного решения внезапных проблем. Говорить будем в контексте производительности приложений, но многие идеи и подходы могут пригодиться в любой технической деятельности.

Тема перформанс-анализа очень большая, но в ней можно выделить четыре основных задачи:

• Анализ распределений. Он даёт ответ на вопрос о том, какова продолжительность некоторой операции. Увы, если мы N раз замерим один и тот же метод, то получим N разных значений. А как их агрегировать — не очень понятно. Часто можно услышать, что вроде бы брать среднее — плохо, брать медиану — плохо, брать любую другую метрику — тоже плохо.
• Сравнение бенчмарков. Вот есть у нас два варианта алгоритма, и нужно понять, какой из них быстрее. Но если начать мерить, то порой оказывается, что в половине случаев быстрее первый, а в другой половине — второй. Как в этом случае принять бизнес-решение о выборе правильного алгоритма для продакшна — тоже не очень понятно.
• Анализ истории. Гоняется, скажем, набор некоторых тестов на CI-сервере после каждого коммита. И вроде есть ощущение, что по этим данным мы можем обнаружить моменты, в которые всё стало работать медленнее. Но из-за шума и большого разброса значений логика обнаружения вызывает огромное количество трудностей.
• Написание перформанс-тестов. Это мечта многих разработчиков и тестировщиков — написать некоторую логику и сказать ей: не регрессируй по производительности. Если логика стала работать медленнее, то тест должен сразу упасть. А если не стала — то не должен. Звучит просто ровно до того момента, когда вы попытаетесь написать такой тест. У большинства моих знакомых первые 30 попыток оказываются неудачными, после чего они бросают это занятие.

Источники вдохновения

Сегодня я буду много рассказывать о различных подходах и алгоритмах для решения этих задач. Появились эти подходы не на пустом месте, а в результате многолетнего опыта работы над несколькими проектами.

Первый из них — BenchmarkDotNet. Это библиотека для точных и надёжных замеров перформанса .NET-приложений, которую я начал делать семь лет назад как маленький pet project. К сожалению, с ним случилось самое страшное, что вообще может случиться с опенсорс-проектом: он стал популярным. Сейчас у проекта тысячи пользователей и миллионы скачиваний.

А страшно это потому, что все эти пользователи постоянно пишут мне и задают разные вопросы. И самый популярный вопрос звучит так: «Ну, вот замерил я производительность, получил какие-то циферки, а дальше-то что делать?» И это очень хороший вопрос. Действительно, далеко не всегда понятно как анализировать результаты замеров.

Тогда я решил завести ещё один проект — Perfolizer. В нём я потихоньку собираю разные алгоритмы для перформанс-анализа, которые доступны в виде NuGet-пакета и в виде command line-тулов. Сначала пользователи радовались, но потом они начали задавать новый вопрос: «Ну, применил я эти алгоритмы, получил какие-то результаты, а дальше-то что делать?» И это тоже очень хороший вопрос, на который я попытаюсь вам ответить сегодня.

А ответ основан на опыте, который я получил в компании JetBrains, работая над проектом Rider. Это кросс-платформенная среда разработки для .NET на базе ReSharper и IntelliJ IDEA. Проект довольно большой: в нём несколько десятков миллионов строчек кода, и каждый день добавляются сотни новых коммитов. Производительность — это одна из главных фич, которая важна для наших пользователей. Увы, судьба складывается так, что у нас постоянно возникают перформанс-проблемы в самых неожиданных местах. Их нужно оперативно находить, изучать и побеждать. В ходе этой бесконечной борьбы появилось довольно много хороших подходов, которыми я сегодня поделюсь с вами. Давайте же отправимся в волшебную страну перформанс-анализа и разберёмся со всеми этими задачами.

План

— 1. Изучаем сырые данные
— 2. Изучаем сводные метрики
— 3. Применяем статические тесты
— 4. Сравниваем перформансные распределения
— 5. Анализируем историю замеров
— 6. Анализируем точки разладки
— 7. Пишем перформансные тесты
— 8. Допускаем ошибки
— 9. Читаем методическую литературу
— 10. Резюме
— 11. Титры

1. Изучаем сырые данные

И начнём мы с анализа сырых данных. Это отправная точка для многих перформанс-исследований: нужно глазами посмотреть на графики и понять, что там происходит. Давайте попробуем сделать это вместе.

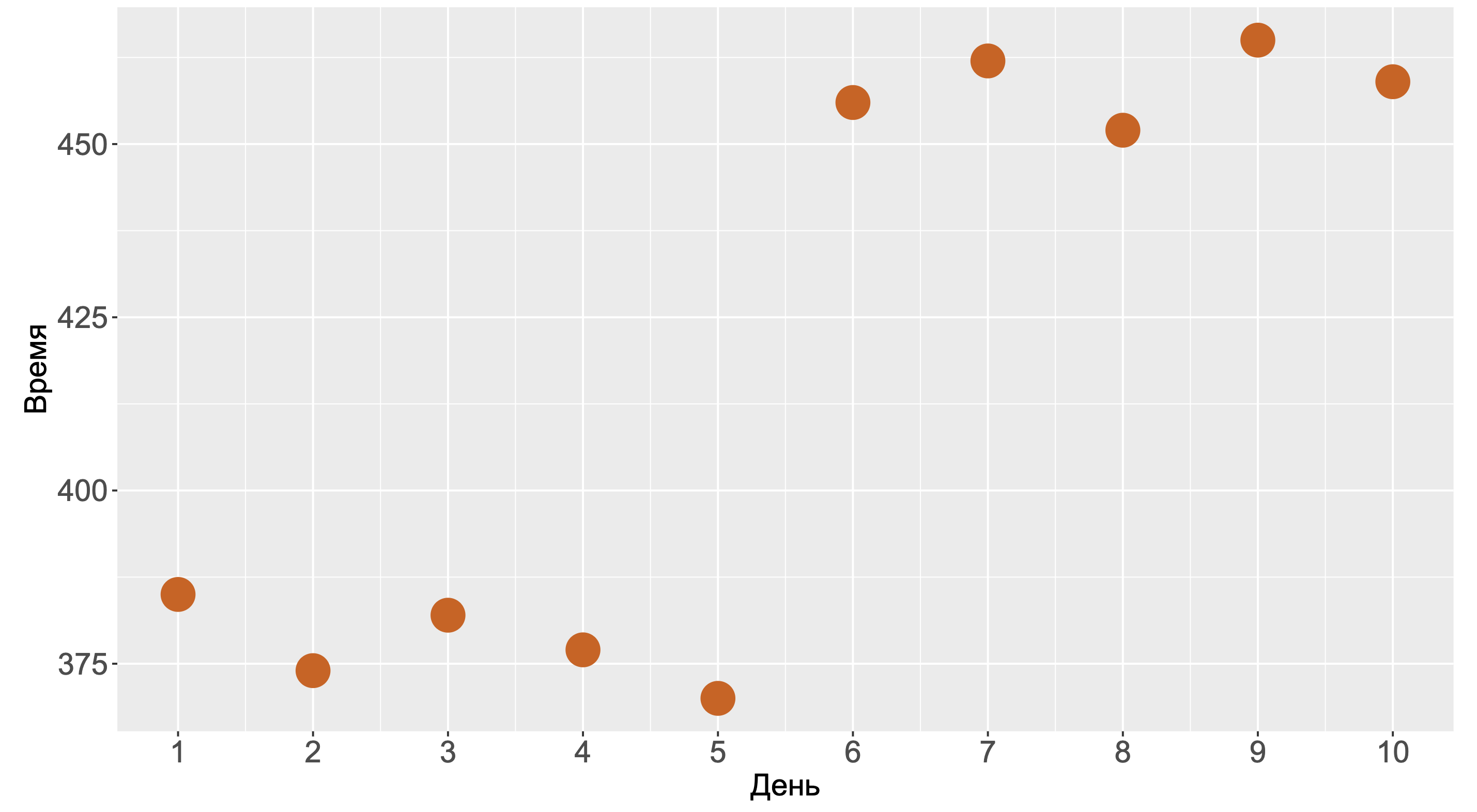
Посмотрите на этот график. За ним скрывается бенчмарк, который мы запускали в течение десяти дней. На каждый день приходится один-единственный замер. С одной стороны, график выглядит так, будто на шестой день у нас произошла деградация. С другой стороны, мы могли получить такую картинку и без деградаций, просто из-за того, что нам не повезло.

Давайте решим вот какую задачку. Допустим, у нас имеется десять тысяч тестов, каждый из которых запускался по разу в течении десяти дней. При этом исходный код никто не меняет, тесты всё время замеряют одно и тоже. Какова вероятность получить хотя бы один подобный график, на котором последние пять замеров больше, чем первые пять замеров?

Для простоты предположим, что форма распределения нам известна и она бимодальна. Какова вероятность того, что первые пять замеров будут из первой моды, а последние пять замеров — из второй?

Правильный ответ: 2^–10 или 0,0009765625. Вроде выглядит как довольно маленькая вероятность, но давайте вспомним, что у нас десять тысяч тестов. Несложно подсчитать вероятность того, что хотя бы на одном тесте мы получим такую псевдо-деградацию. Получится практически 100%.

В качестве упражнения попробуйте обобщить эту формулу на случай произвольного распределения и посмотрите, что получится там. А мы продолжим работать с нашей моделью и посмотрим на зависимость вероятности от количества тестов.

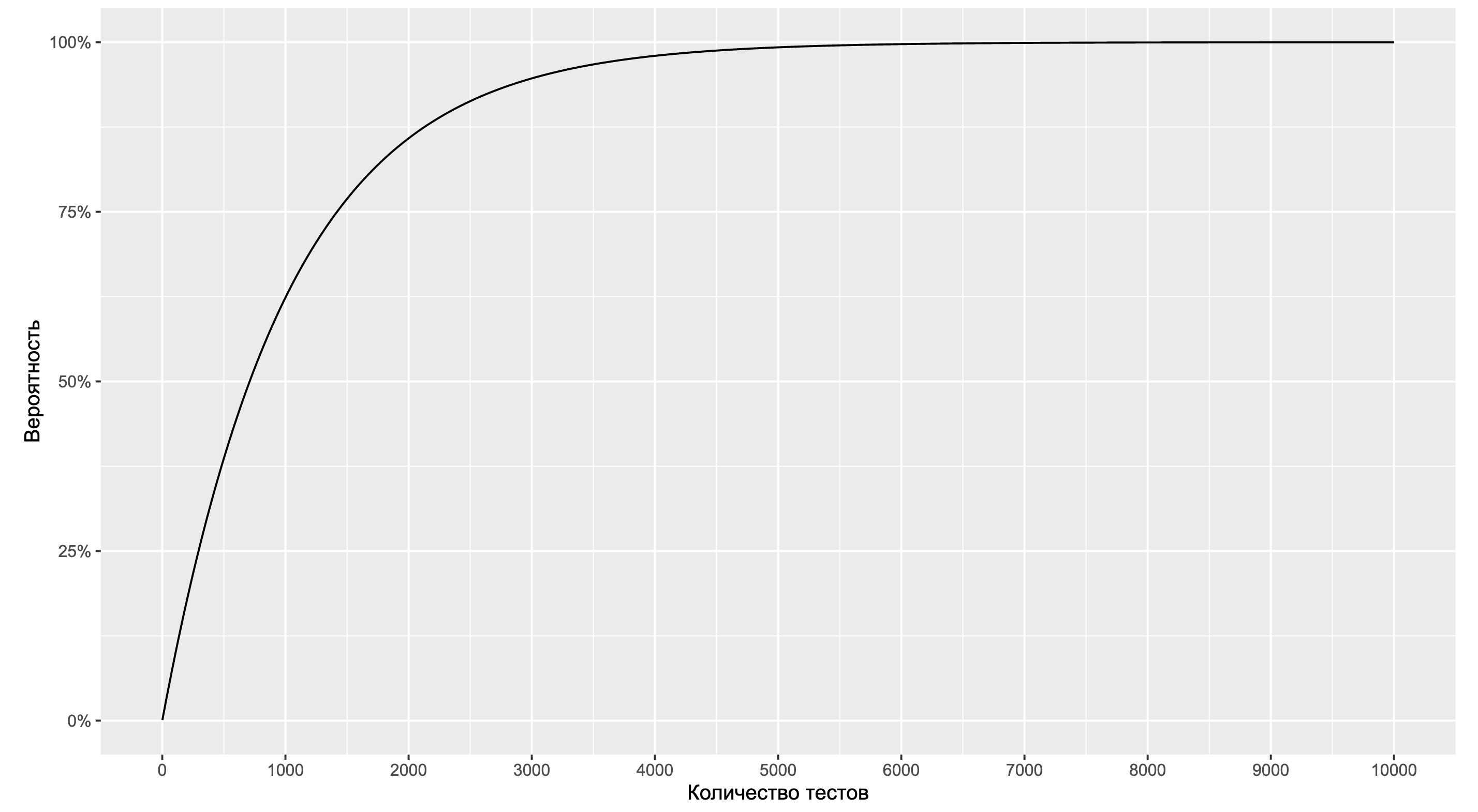
Как можно видеть, мы приближаемся к 100% уже на 5000 тестов. А это довольно маленькое количество тестов по энтерпрайзным меркам. Если же мы обобщим форму распределения и начнём искать другие типы ситуаций с подозрительными графиками, то мы имеем все шансы их найти уже на 1000 тестов. Если систематически смотреть на эти графики, то скорее всего мы быстро наткнёмся на подобные картинки. И тут начинаются проблемы, так как наш мозг очень любит искать паттерны.

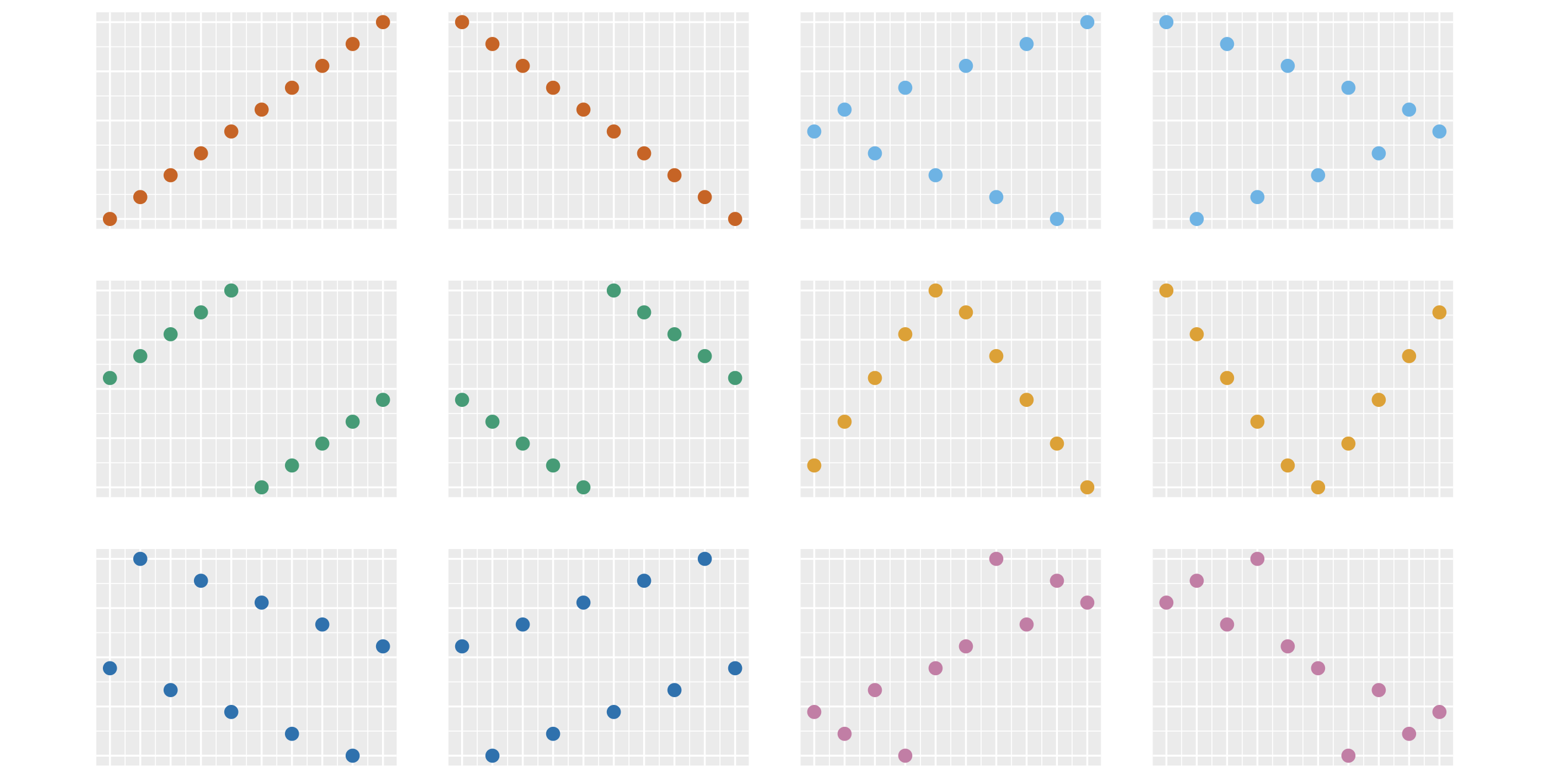
Сейчас вы видите 12 разных картинок. На каждой изображены 10 точек. Набор ординат точек на всех картинках одинаковый, отличается только их порядок. При большом количестве тестов велика вероятность получить любую из этих картинок совершенно случайно. Однако у нашего мозга есть удивительная способность видеть структуру и взаимосвязи в случайных и бессмысленных данных. По научному такой феномен называется апофения.

Даже на полностью рандомных данных человек всегда найдёт несколько ситуаций, когда захочется сказать: «Мы никак не могли получить такую картинку случайно, тут явно есть закономерность!» На этом свойстве нашего мозга базируется большое количество разных когнитивных искажений. Последствия бывают самые разные.
От веры в то, что танец с бубном поможет ускорить программу, до десятков бесполезных часов, которые проведены в поисках проблемы, которой на самом деле нет.

Кто лучше всех разбирается в перформанс-анализе?

На эту тему написано большое количество статей, но я решил для верности провести собственный эксперимент. В течение долгих недель я методично изучал разные перформанс-графики и пытался отгадать ситуации, в которых у нас есть проблемы.
В какой-то момент я решил начать записывать, насколько хорошо у меня получается. Процент успешных угадываний составил 20–30%. Это не так уж и плохо, лучше, чем у многих моих коллег.

Но я задался вопросом: «Можно ли угадывать ещё лучше?» Тогда я сделал из этих графиков набор задачек, в которых нужно было найти деградации. Ответ можно было дать автоматически, нажимая клавиши на клавиатуре. Я пошёл с этим набором к начальнику нашего .NET-отдела и попросил прорешать задачки… его кошку Осю. Сначала Ося восприняла эту идею без особого энтузиазма. Но вскоре её удалось усадить за клавиатуру, чтобы она нажимала на клавиши и давала ответы на задачки. Процент угадываний получился 45–55%.

Таким образом, Ося — намного более квалифицированный интуитивный перформанс-инженер, чем я. Увы, работать у нас фултайм Ося не захотела. К счастью, её логику принятия решений удалось аппроксимировать монеткой. Орёл — есть деградация, решка — нет деградации. Такой подход позволяет значительно улучшить качество анализа.

Общий вывод: сырые данные контринтуитивны и обманчивы. Даже если у вас большой опыт разбора всяких графиков, интуиция может создавать большое количество трудностей. И можно было бы продолжать пользоваться монеткой, но монеток на все расследования не напасёшься. Да и вручную смотреть на все эти графики довольно утомительно. Хочется иметь более доступный, надёжный и автоматизированный инструмент.

2. Изучаем сводные метрики

В такие моменты программисты начинают рассуждать о том, что нужно как-то агрегировать наши данные. Мол, надо подсчитать какие-то сводные метрики, засунуть их в умную формулу, и всё сразу станет хорошо.

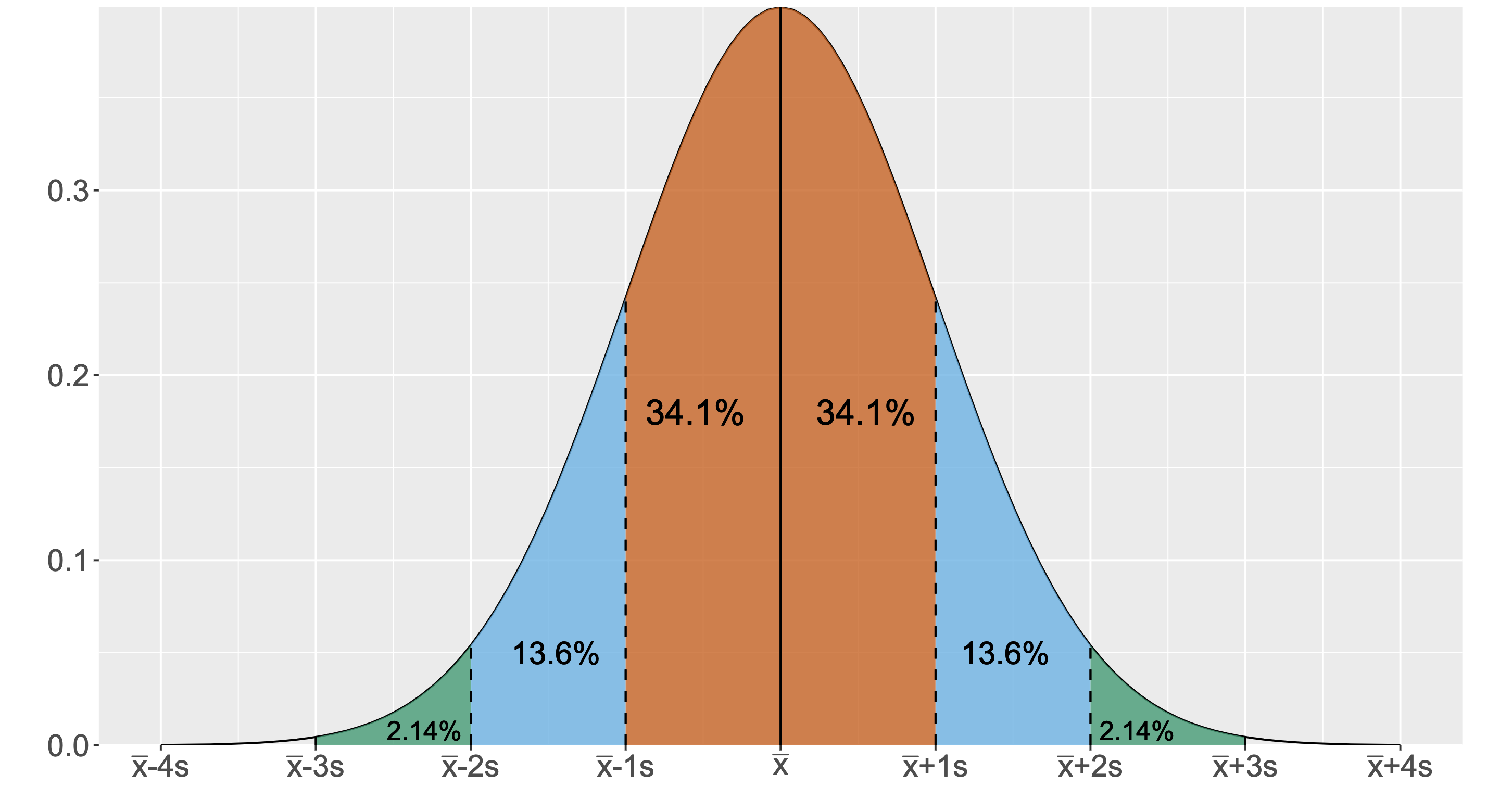
При работе с этими метриками в голове часто возникает картинка нормального распределения. Скорее всего, вы видели подобную картинку в учебниках по матстатистике. Однако сомневаюсь, что встречали нормальное распределение в реальной жизни.

Нужно признать, что нормальное распределение действительно возникает в некоторых предметных областях при определённых математических построениях. Но на сырых перформансных данных вероятность встретить идеальное нормальное распределение практически нулевая. Поэтому дальше мы будем полагать, что условие нормальности не выполняется. Распределение может иметь сколь угодно странную форму. Но, увы, людям инстинктивно хочется использовать нормальное распределение в качестве ментальной модели. Его проще всего себе представить. Давайте проведём эксперимент.

Посмотрите на эту таблицу и постарайтесь сходу сказать, какой из двух методов быстрее. Большинство людей смотрят только на среднее значение и игнорируют остальные метрики, так как с ними довольно сложно работать.

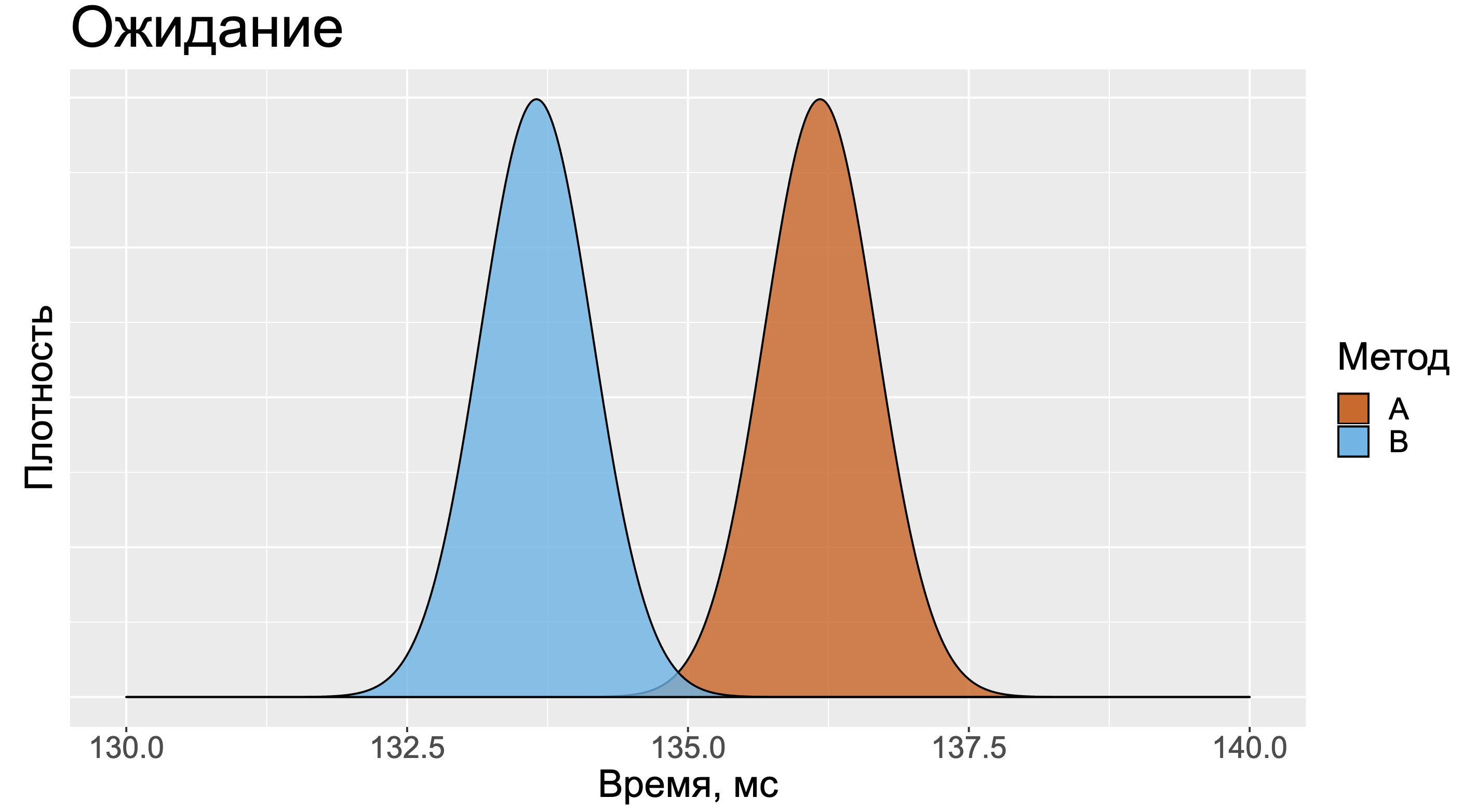
В данном случае хочется представить два примерно одинаковых нормальных распределения. Распределение для метода А будет немного правее, так как среднее значение замеров у него больше.

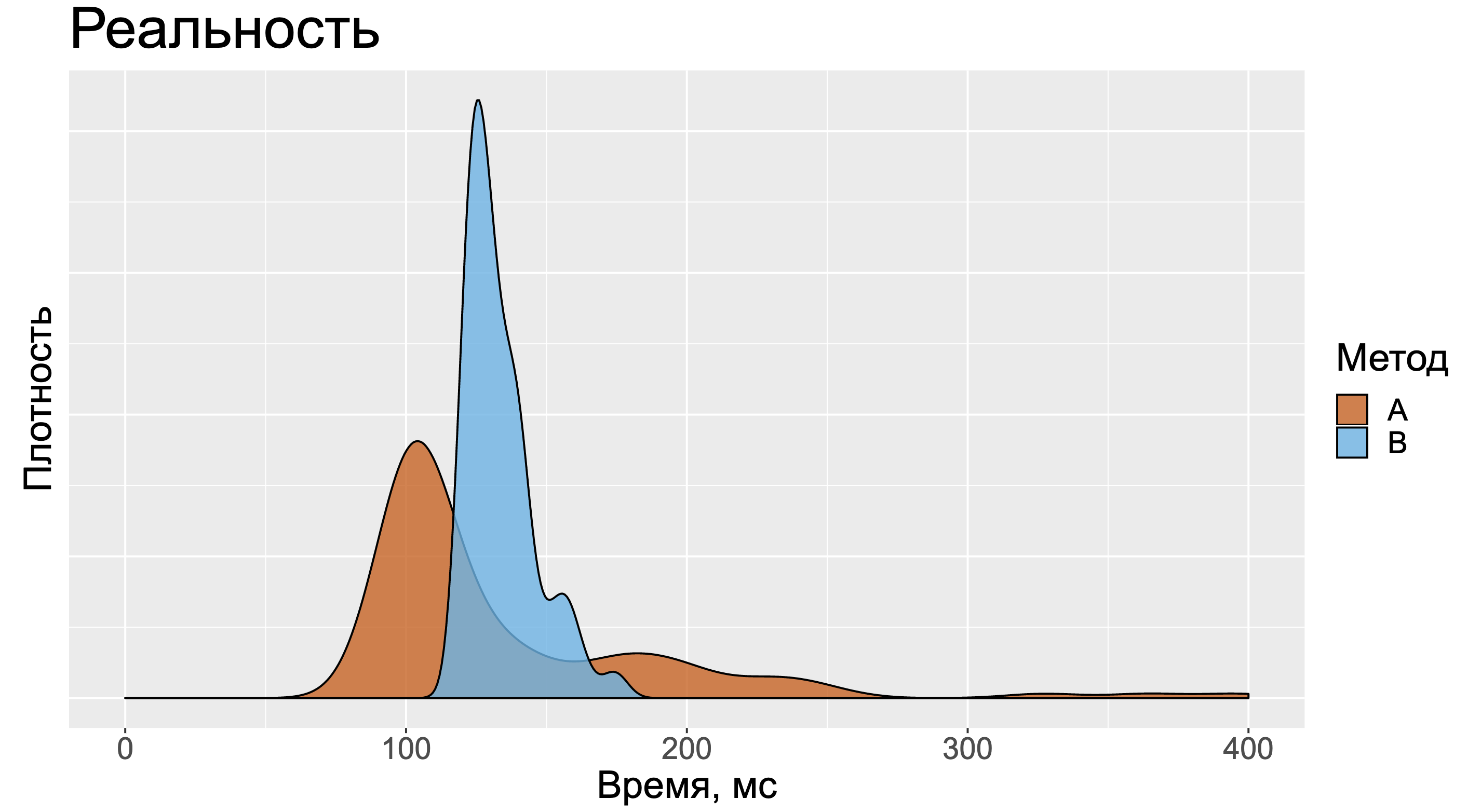
Но в реальности картинка может оказаться более сложной. Для методов А и B нельзя сказать кто быстрее. Когда-то быстрее А, когда-то быстрее B. И вроде бы большое значение стандартного отклонения должно было нас немного насторожить.
А тот факт, что медиана замеров метода А намного меньше медианы замеров метода B, должен был бы нас взволновать ещё сильнее.

Увы, в реальной жизни появляется привычка игнорировать дополнительные метрики. Особенно, если вы изучаете большое количество сводных таблиц с результатами бенчмарков. Слишком уж напряжно смотреть сразу на дюжину разных метрик, удерживать их в голове и пытаться сопоставить их друг с другом. Эффект обманчивости сводных метрик хорошо описан в научной литературе.

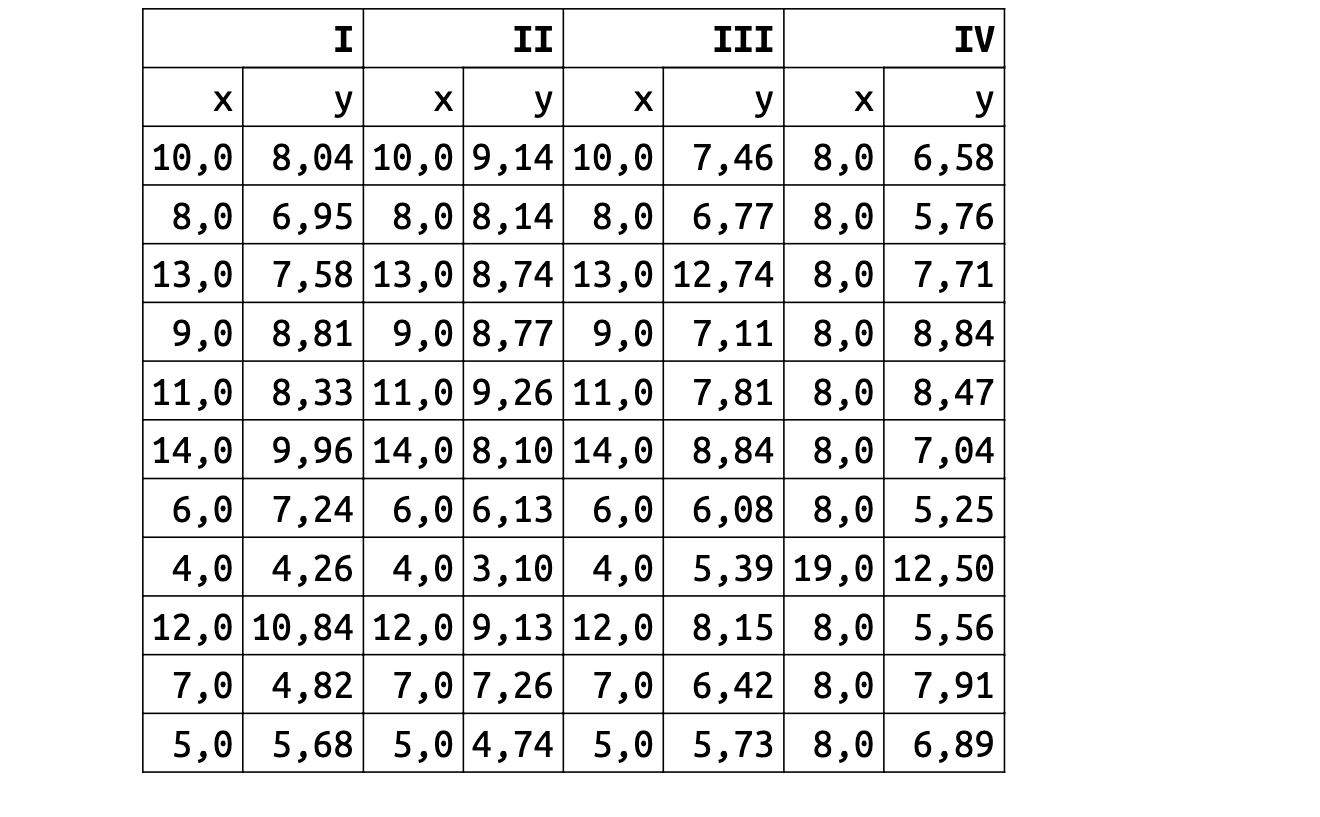
Одним из классических примеров подобной проблемы является квартет Энскомба 1973 года. Он состоит из четырёх наборов данных, в каждом из которых есть 11 пар значений x и y. Анализировать подобные сырые данные глазами тяжко. Поэтому возникает желание посмотреть на метрики.

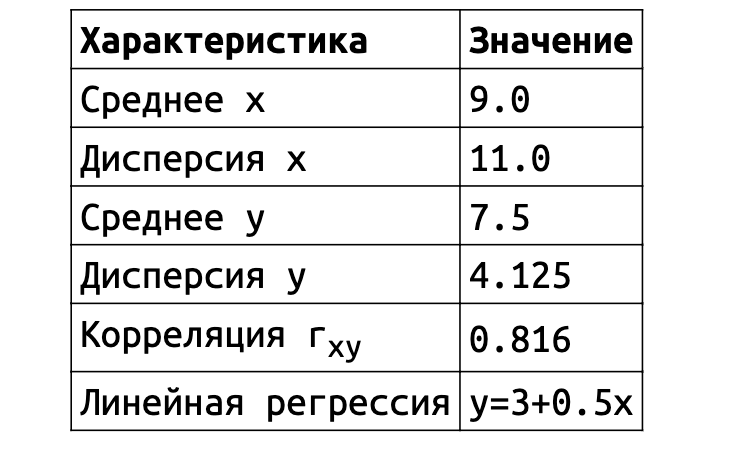
И тут начинается самое интересное. Значения средних, дисперсии, корреляции и формулы линейной регрессии оказываются практически одинаковыми для всех наборов данных.

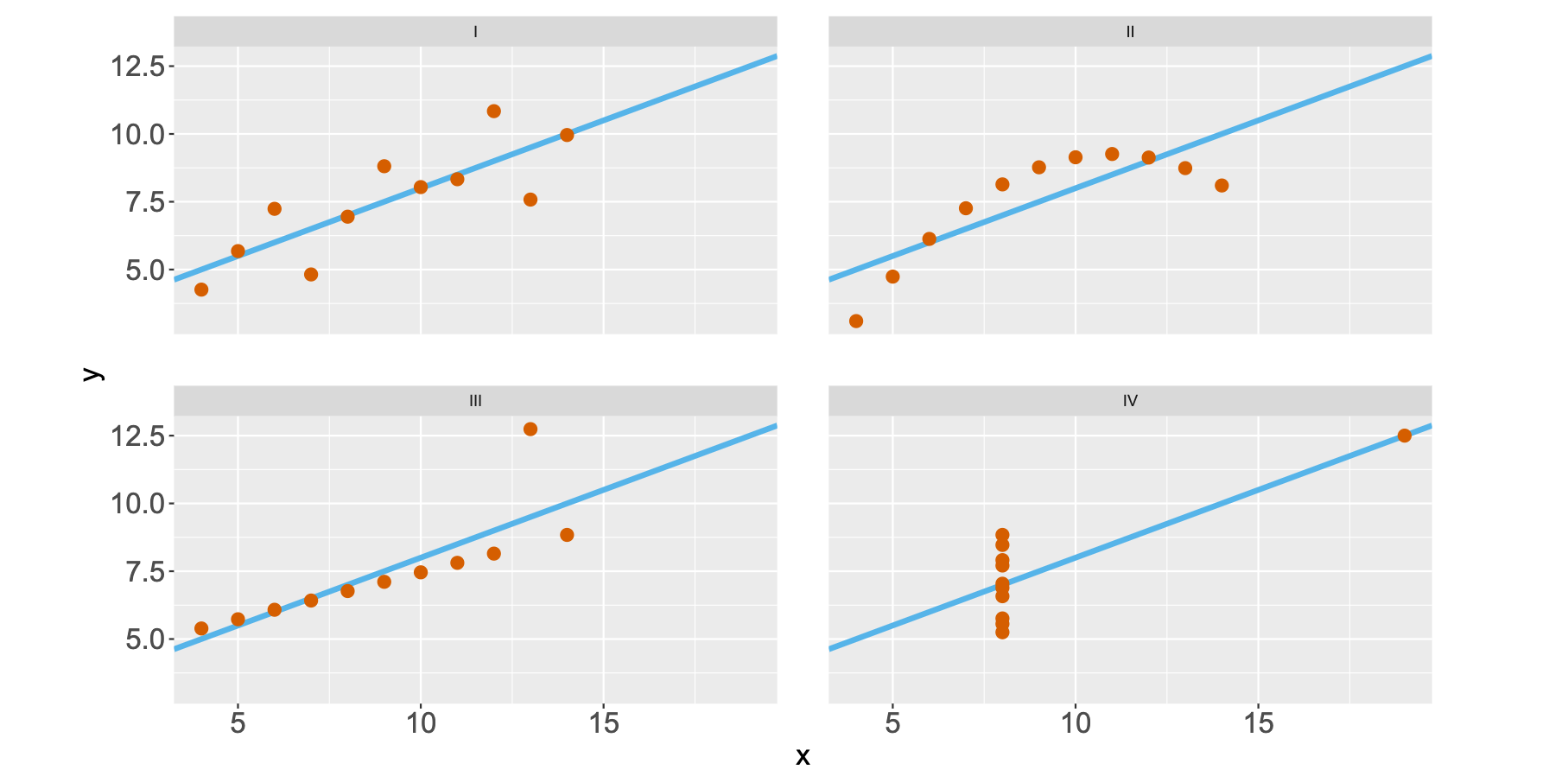
Однако форма этих данных абсолютно разная. Классические метрики скрывают от нас эту информацию. Даже если вы очень круто разбираетесь в матстатистике, вы не сможете обнаружить разницу между наборами данных только по метрикам. Просто потому, что такова их природа.

Из более свежих работ хочется отметить статью 2017 года "Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing", в которой пара канадских учёных нарисовала очаровательный набор разных картинок с одинаковыми значениями средних, дисперсий и корреляций.

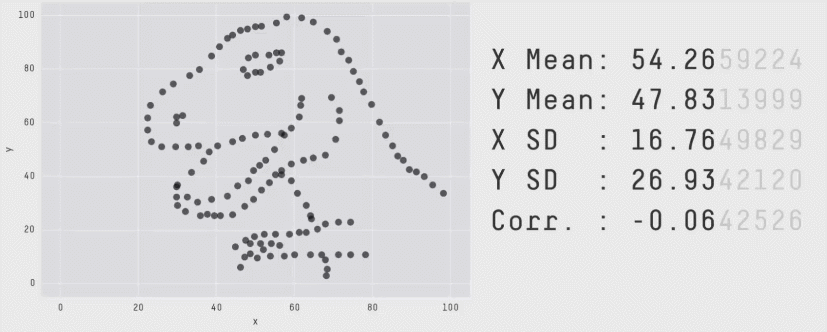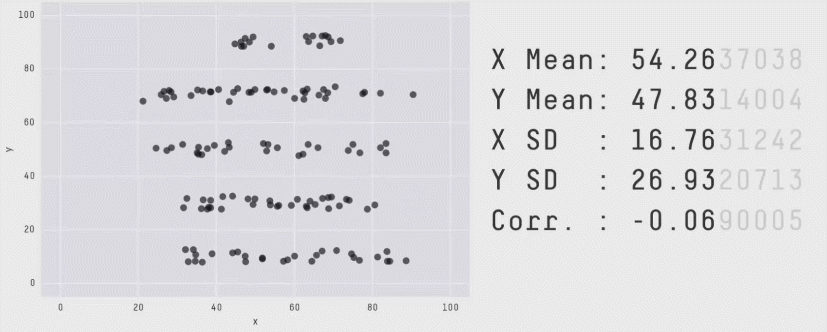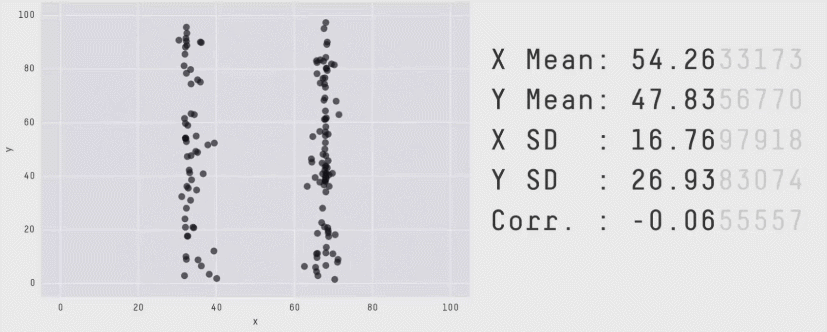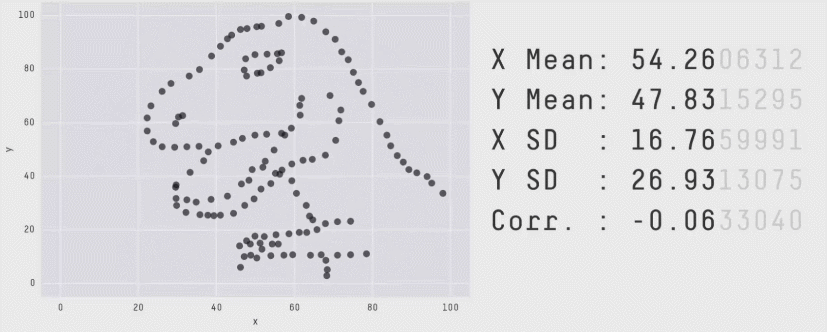
Ситуация аналогична квартету Энскомба: сводные метрики совпадают, но форма данных кардинально различается. И это грустно, так как вся классическая статистика построена на подсчёте каких-то странных метрик и попытках извлечь из них полезную информацию. Попытки победить в подобной угадайке могут обернуться провалом. Хочется создать подход, в котором статистические отчёты не будут нас обманывать столь подлым способом.

Статистика должна быть дружелюбной

К счастью, у нас есть компьютеры, с помощью которых мы можем сделать статистику более дружелюбной. Сейчас я покажу вам один из способов, который можно эффективно использовать на практике.

Основная идея в том, что мы будем описывать распределения с помощью интервалов, в которые попадает основная масса значений. Ведь именно это нас на самом деле интересует на первом этапе перформанс-исследования. Нам хочется примерно узнать сколько времени занимает тот или иной метод. Ответ «примерно 100–200 мс» зачастую нас вполне устроит.

Обычно мы пытаемся сами домыслить такой интервал по среднему и дисперсии, используя нормальное распределение в качестве ментальной модели. Почему бы не подсчитать такой интервал сразу? Но тут истинные математики возмутятся: «Как же мы будем сравнивать распределения без классических метрик? А что, если у нас есть большие выбросы?» Это может быть для нас важно, но эта информация в табличке отсутствует.

К счастью, обладая базовыми навыками программирования, можно легко обнаружить такие ситуации и отобразить эту информацию в табличке.

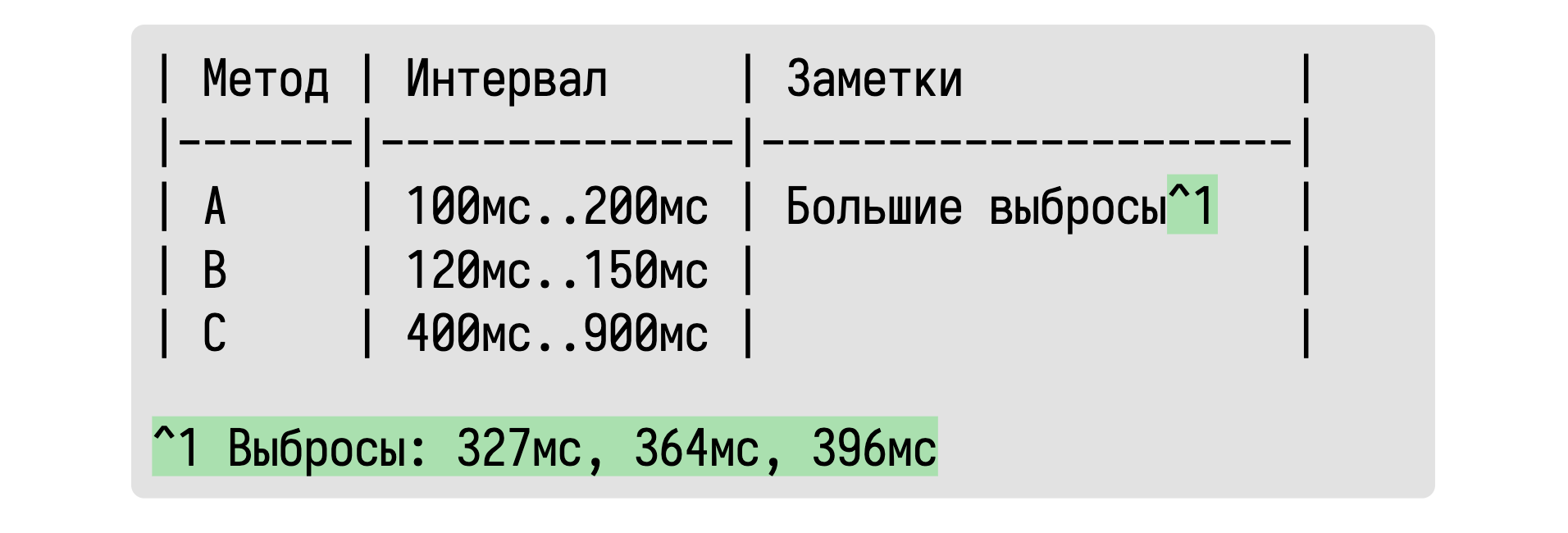
Если нас волнуют конкретные значения выбросов, то мы их можем также выписать. А что, спросите вы, если какой-то интервал оказался очень неточным из-за маленького размера выборки?

Про это тоже можно написать.

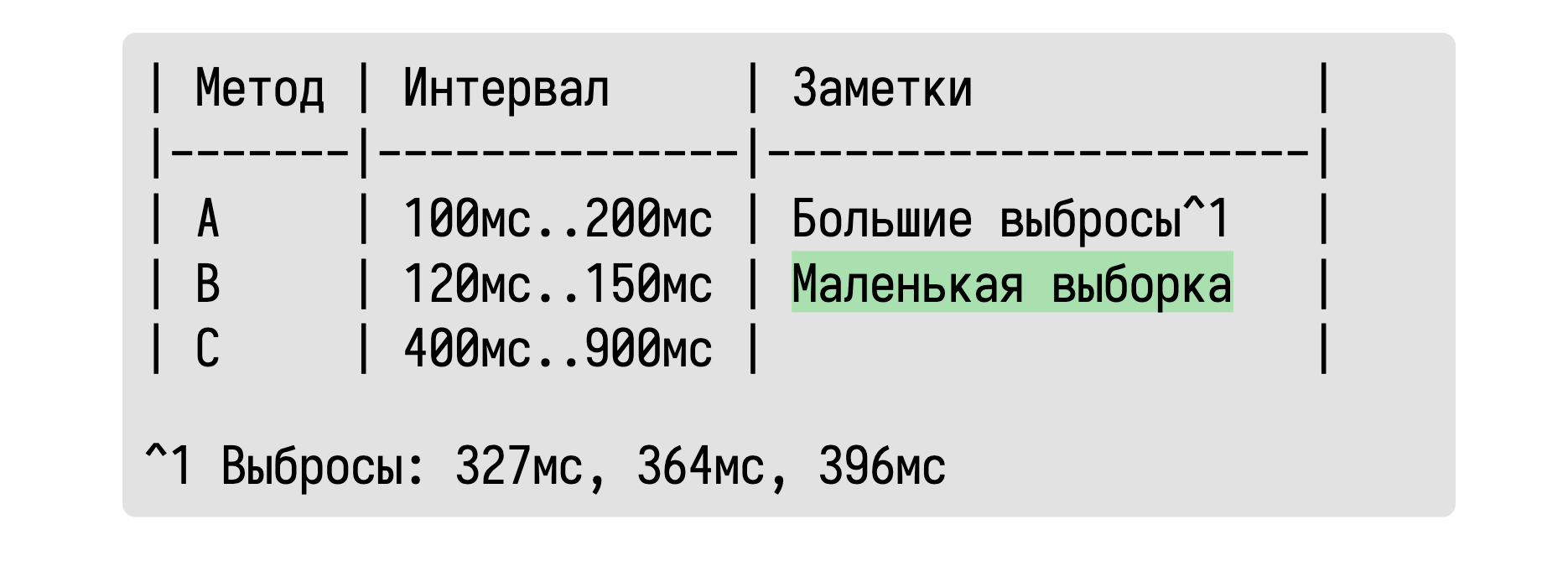
Если выборка слишком мала для получения достоверного результата, то можно просто это указать.

А что, спросите вы, если у нас распределение мультимодальное? Мы не сможем об этом узнать по такой табличке!

Мультимодальность тоже отлично обнаруживается.

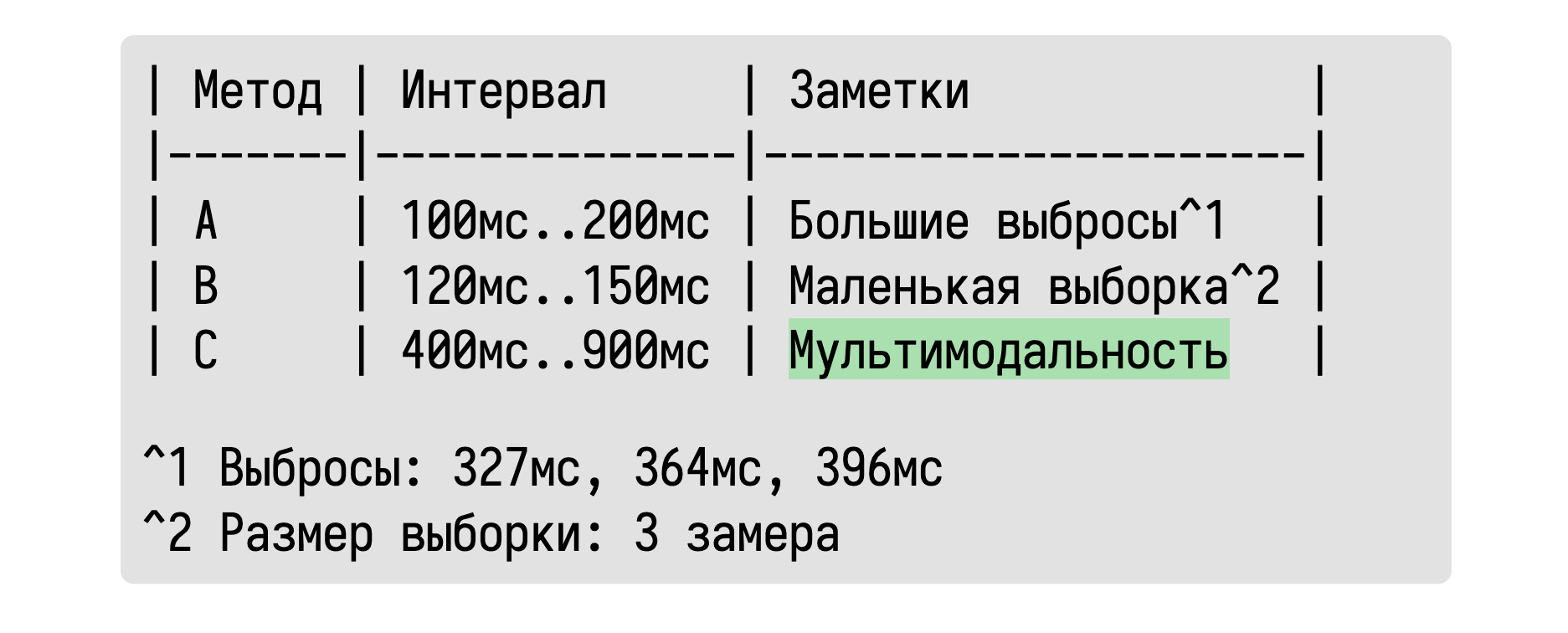
А если внутри нашего интервала существуют два или более подынтервалов, которые содержат основную массу значений, то давайте просто напишем об этом.

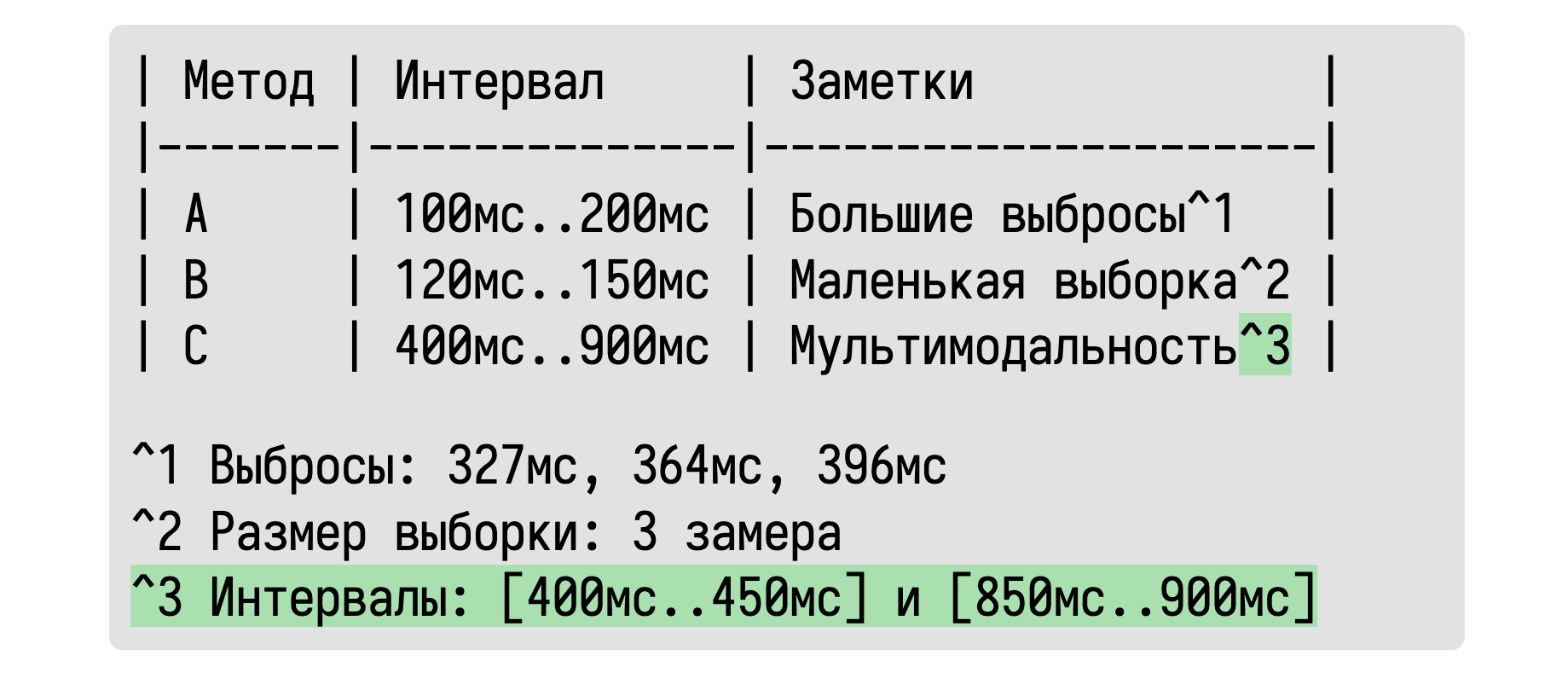
В классических статистических подходах мы должны угадывать подобные эффекты по непонятным для многих значениям дисперсии, стандартных ошибок, квантилей и прочих не особо легко интерпретируемых метрик. Вместо этого мы можем обнаружить все эти эффекты автоматически и вывести предупреждение о них только в тех случаях, когда это важно.

Источники шума и модальности

Необходимо также хорошо понимать, откуда берутся подобные распределения.
Программы исполняются в довольно сложных окружениях, где много разных факторов могут повлиять на ваши замеры. Вот основные источники:

• Планировщик операционной системы: он сам решает, когда будет исполняться ваш бенчмарк и как будет делиться ресурсами с другими процессами.

  
  

• Многопоточность: как только в программе появляется несколько потоков и хотя бы одна блокировка, программа вовсе становится недетерминированной. Из-за этого может появляться и мультимодальность, и очень большой разброс значений.

  
  

• Выравнивание кода и данных: производительность может очень сильно зависеть от того, в какие области оперативной оперативной памяти вы попали.

  
  

• Кэш процессора — ещё один заклятый враг любого перформанс-инженера. От его состояния производительность многих алгоритмов может скакать в несколько раз.

  
  

• Изменение частоты процессора: современные компьютеры могут динамически менять частоту CPU по собственному усмотрению.

  
  

• Термальный троттлинг — мой любимый пример на эту тему. Идея проста: если ваш любимый ноутбук перегрелся, то частота процессора может заметно упасть, чтобы вашим коленкам было не так горячо.

  
  

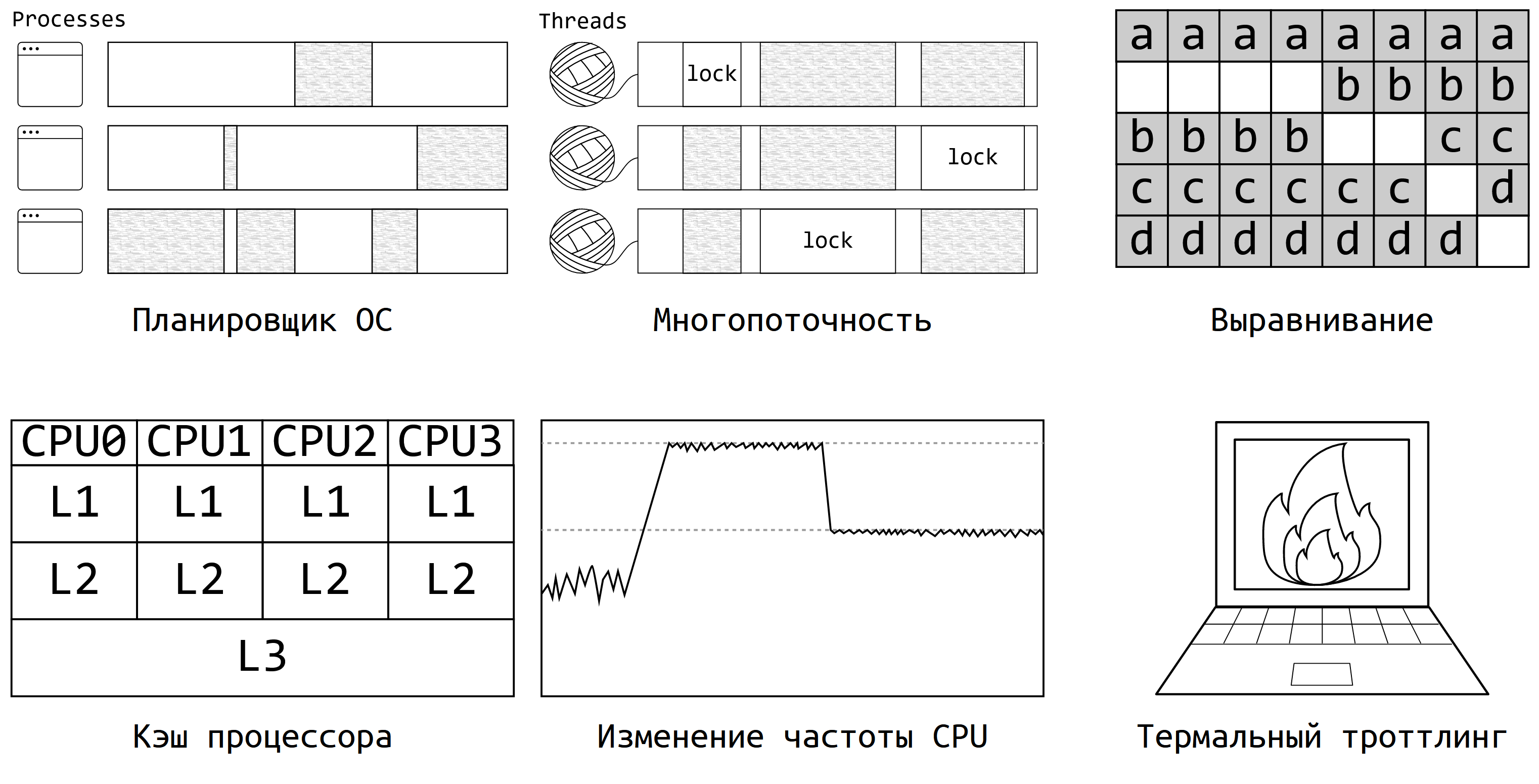
Я очень люблю рассказывать про то, как термальный троттлинг легко можно пронаблюдать в домашних условиях.

Давайте возьмём макбук и поместим его в два разных физических окружения. В первом случае он будет лежать в морозилке, а во втором будет завёрнут в одеялко вблизи керамического тепловентилятора. С помощью тепловизора можно убедиться в значительной разнице между температурами ноутбука в каждом из случаев. В морозилке мне удалось довольно легко удержать частоту на уровне 3,5 ГГц.
Запустив любой CPU-bound бенчмарк можно получить набор эталонных замеров. В одеялке же макбук быстро начинает перегреваться и скидывает частоту до базовых 2,5 ГГц.

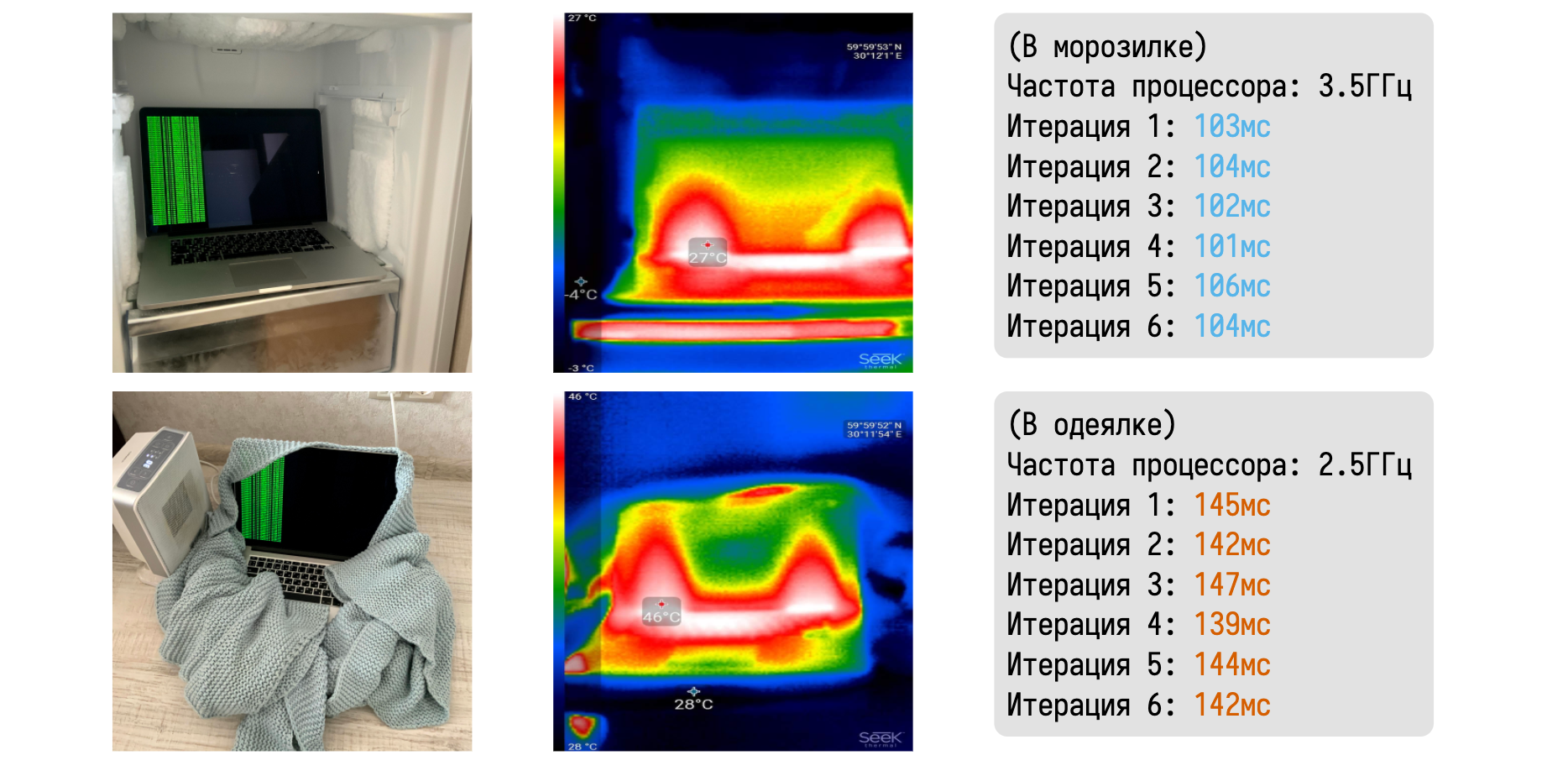
Результаты нашего бенчмарка сразу начинают драматически деградировать. Знание таких феноменов очень помогает при анализе значений замеров. На всех наших перформанс-агентах мы всегда записываем температуру процессора до и после бенчмарка. При возникновения троттлинга в логи пишется жирное предупреждение о недостоверности результатов. Подобные автоматические проверки хорошо дополняют дружелюбную сводную таблицу, показывая не только наличие странных феноменов в распределениях, но и их возможные причины.

Можно очень долго рассказывать о конкретных анализах и проверках, но мне хочется, чтобы вы запомнили основную идею: статистика может быть дружелюбной. Более того, она должна быть дружелюбной.

Вместо того, чтобы играть в угадайку при анализе обманчивых сводных метрик, можно сразу выводить те факты, которые мы хотим знать о наших замерах. С помощью этого мы легко можем решить нашу первую-перфоманс задачу по анализу распределений.

3. Применяем статистические тесты

Теперь можно перейти второй задаче по сравнению двух распределений. Скажем, есть у нас две версии алгоритма, нужно понять, есть ли между ними значительная разница в производительности.

Если вы погуглите на эту тему, то быстро наткнётесь на советы по использованию тестов на статистическую значимость. Ну что ж, давайте попробуем пойти этим путём, который довольно распространён в современном мире. Прежде всего, взглянем на типичную деградацию, которую нам хотелось бы уметь обнаруживать.

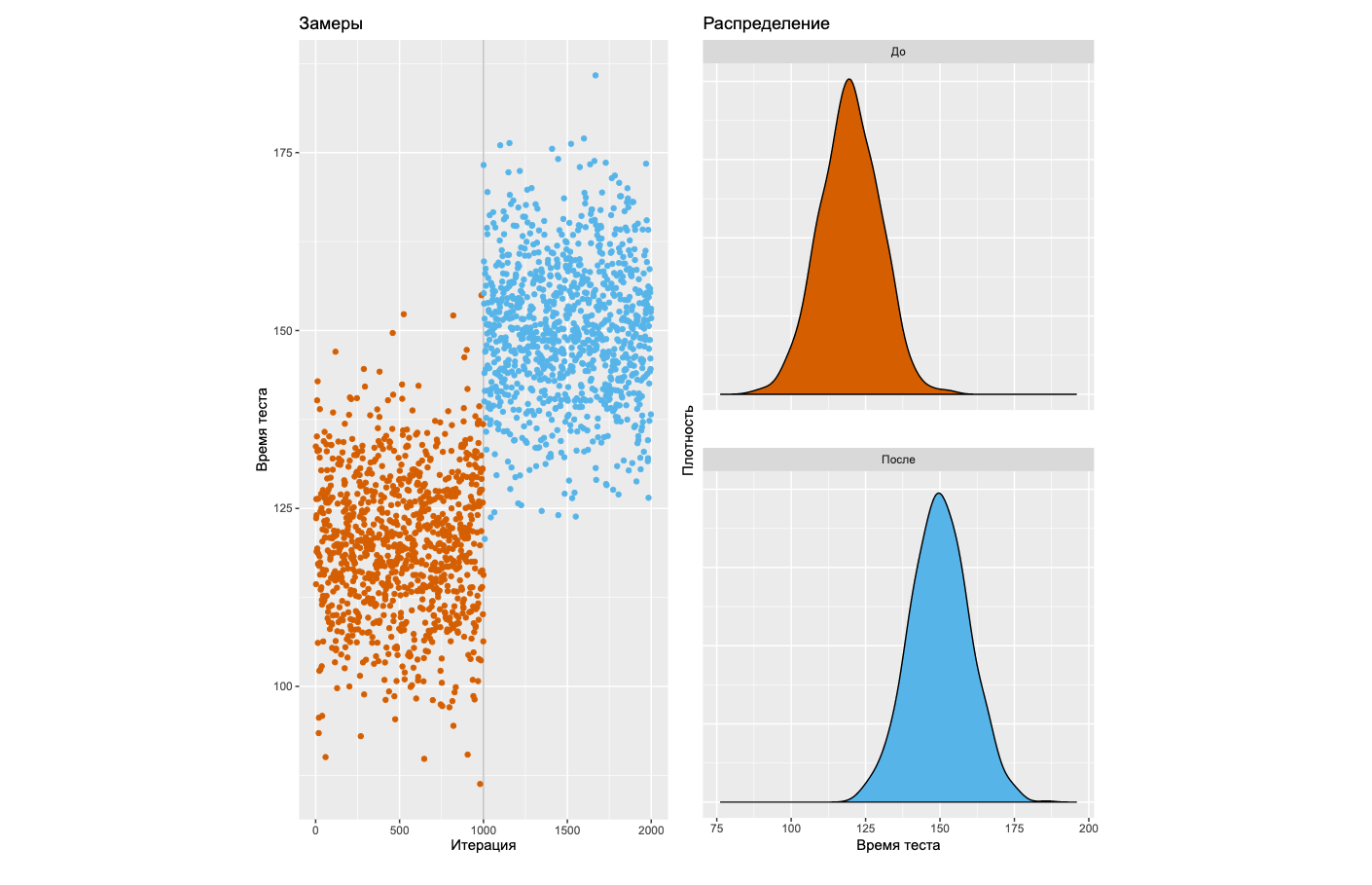
Слева вы видите график замеров некоторого бенчмарка на 2000 итераций. Детектор паттернов в вашем мозге мгновенно говорит, что после тысячной итерации произошла явная деградация. Справа можно посмотреть на плотности распределений до и после этого загадочного момента. Давайте научимся детектировать подобные ситуации с помощью статистических тестов!

Тут мы встречаем первую проблему: разных тестов очень много. Какой из них использовать — не очень понятно. Но давайте предположим, что мы выбрали какой-то тест. Неважно какой, они все работают примерно по одной схеме.

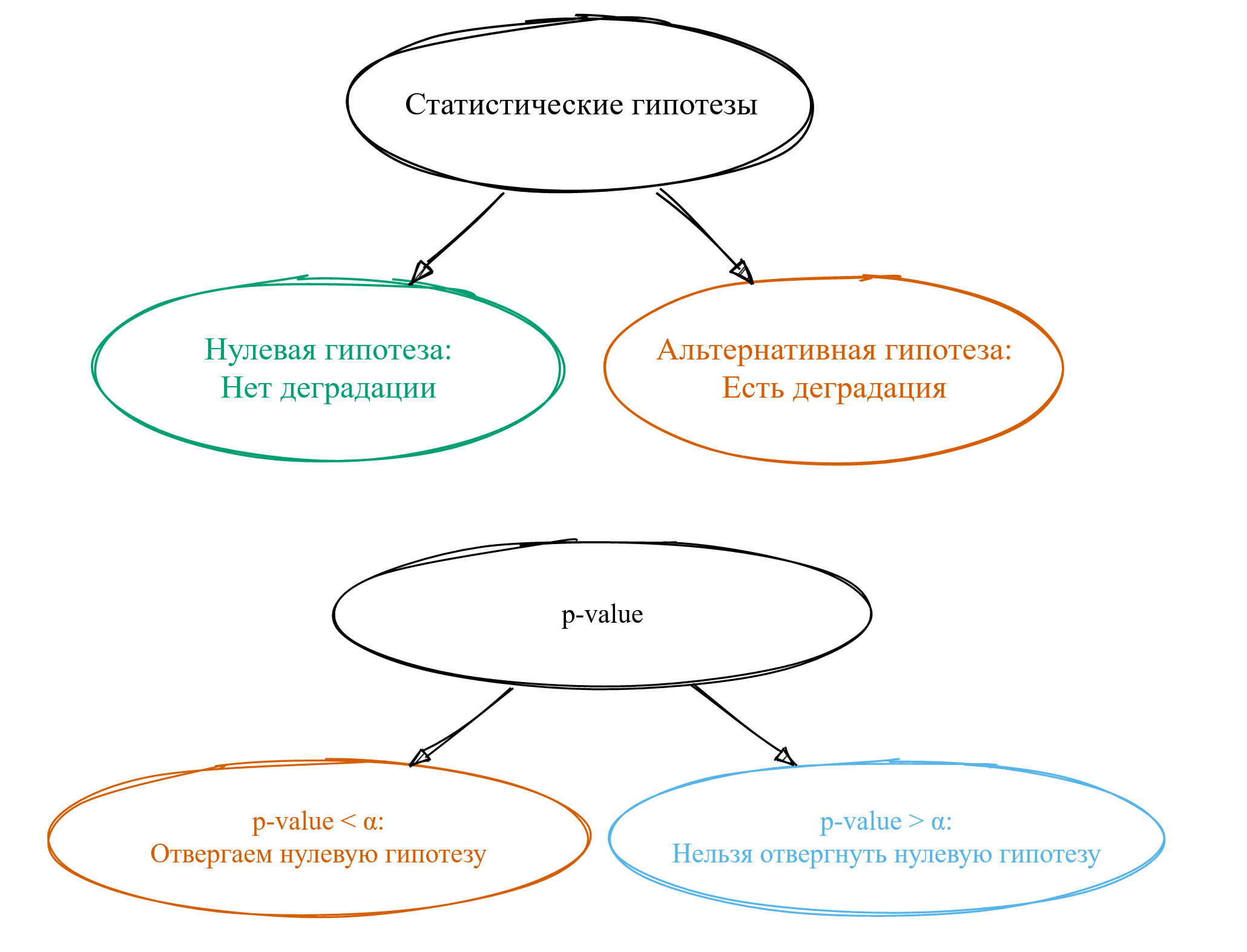
Прежде всего, нам нужно сформулировать так называемые статистические гипотезы. Обычно их две. Первая называется нулевой гипотезой: она будет нам говорить о том, что у нас нет деградации. Вторая называется альтернативной гипотезой: она говорит нам о том, что у нас есть деградация. Как по мне, термины ужасные — в современном мире такой нейминг никогда бы не прошёл code review.

Забавно, что термин «альтернативные гипотезы» придумали Нейман и Пирсон в 1933 году, но термин «нулевая гипотеза» им не особо нравился. Его придумал Фишер спустя два года, но идея использования альтернативных гипотез ему не очень нравилась.
В общем, имеющееся именование — это исторический курьёз, который магически распространился по научной литературе. И теперь это легаси с нами навсегда.

В результате применения статистических тестов обычно получается магическая метрика под названием p-value. Мало кто понимает, что она означает, но основная масса пользователей статистических тестов научились её использовать.

Если p-value оказалось меньше некоторой константы α, то мы говорим об отвергании нулевой гипотезы. Из такого утверждения хочется сделать вывод о том, что у нас есть деградация, но это далеко не всегда так.

Если же p-value оказалось больше магической константы α, то говорят, что «нельзя отвергнуть нулевую гипотезу». Тут начинаются большие сложности с интерпретацией, а смысл фразы остаётся для многих загадкой. Путём сложной цепочки логических выводов люди приходят к тому, что, наверное, это означает, что деградации всё-таки нет. Однако на самом деле это означает, что чёрт его знает, есть ли у нас деградация или нет — не совсем тот результат, который мы хотели бы получить. Но давайте продолжим вспоминать матчасть.

Статистические ошибки

Давайте взглянем на самые главные ошибки, которые можно допустить:

• Ошибка первого рода: деградации на самом деле нет, но мы думаем, что есть. Так называемый false positive.
• Ошибка второго рода: деградация есть, но мы думаем, что её нет. Это false negative.
• Ошибка третьего рода: ситуация, когда мы получили ответ не на тот вопрос, на который мы хотели ответить. На мой взгляд, это самая главная ошибка, но её анализом зачастую пренебрегают.

Теперь поговорим о вероятностях этих ошибок.

Вероятность ошибки первого рода обозначается буквой α. Магическое значение по умолчанию, которое все зачем-то используют, составляет 0,05.

Вероятность ошибки второго рода обозначается буквой β. Тут у нас появляется ещё одна магическая константа в качестве значения по умолчанию она равна 0,20.

Вероятность ошибки третьего рода никак не обозначается и её никто не считает, но в среднем по больнице она очень большая.

Давайте теперь поговорим про характеристики статистических тестов и приведённые магические числа.

Самая главная характеристика называется уровень статистической значимости, который совпадает с α.

Одно из первых упоминаний 0,05 в качестве дефолтного значения можно найти в работе Фишера 1935 года. Там всё написано на иностранном языке, поэтому я решил засунуть этот текст в Google Translate и перевести на понятный язык — на C#.

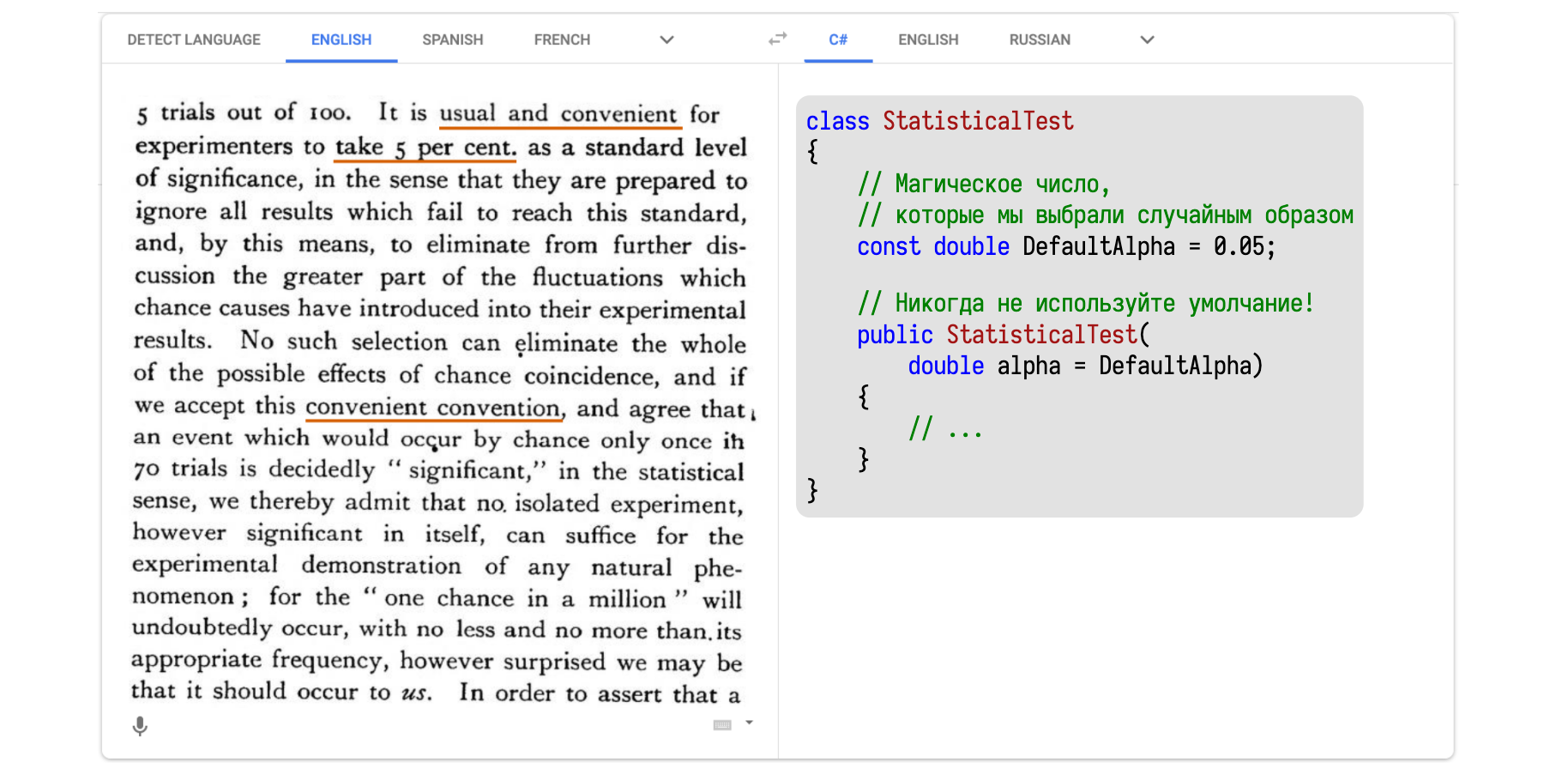
В тексте написано примерно следующее: мол, надо хорошенько подумать, что брать в качестве значения для α, но думать сложно и лень. Поэтому давайте придумаем удобное соглашение о значении по умолчанию, чтобы хоть что-то было, от чего можно отталкиваться. Мотивацию для выбора именно 0,05 можно найти в другой работе Фишера 1926 года в сельскохозяйственном журнале, где он пишет о том, как правильно оценивать эффективность удобрения полей навозом.

Перейдём ко второй характеристике статистических тестов, которая называется статистическая мощность. И равна она не β, как некоторые могли подумать, а 1 — β. Просто потому, что математики очень любят консистентность.

Волшебное число 0,20 можно найти в работе Коэна 1988 года. Тут тоже иностранный язык. Засовываем текст в Google Translate и получаем C#-версию.

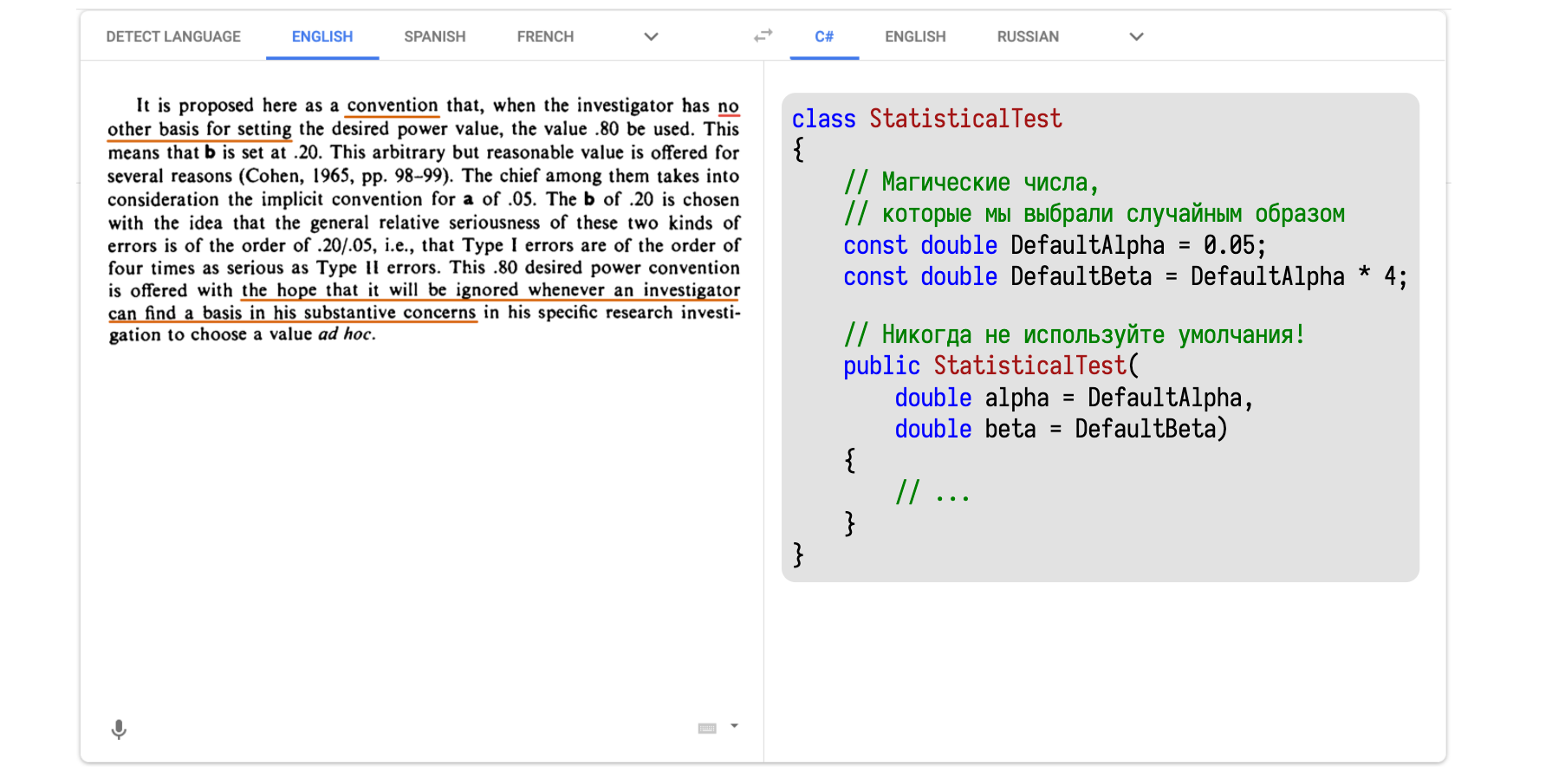
Тут написано, что нужно всегда тщательно думать о том, что взять в качестве β.
И только если у нас совсем нет никаких идей о том, что именно изучается, зачем изучается, то можно взять 0,2. А получилось это число благодаря умножению известных нам 0,05 на 4. Четвёрка тоже взята с потолка.

То есть Коэн умножил одно случайное магическое число на другое случайное магическое число, получил 0,2 и обрёк несколько поколений математиков на использование этого значения в качестве индустриального стандарта.

К счастью, заниматься анализом мощности довольно сложно, поэтому в подавляющем большинстве случаев столь важный этап проведения статистического теста благополучно игнорируется. Но вот с α приходится как-то работать, так как именно с ним сравнивается p-value.

Число очень неудобное и мешает работать, поэтому в случае слишком большого p-value математики придумывают эвфемизмы, чтобы обосновать значимость неудачных исследований: «почти значимый», «положительный тренд», «убедительный результат», «близкий к критическому уровню» и сотни других оправданий появляются в научных статьях каждый год. Особенно страшно становится, когда читаешь статьи по медицине, когда авторы пытаются как-то оправдать потраченные гранты. Но и в перформанс-анализе постоянно возникают проблемы. Просто система спроектирована так, что вызывает дикий соблазн сжульничать и использовать результаты статистического теста некорректным образом.

Использование статистических тестов

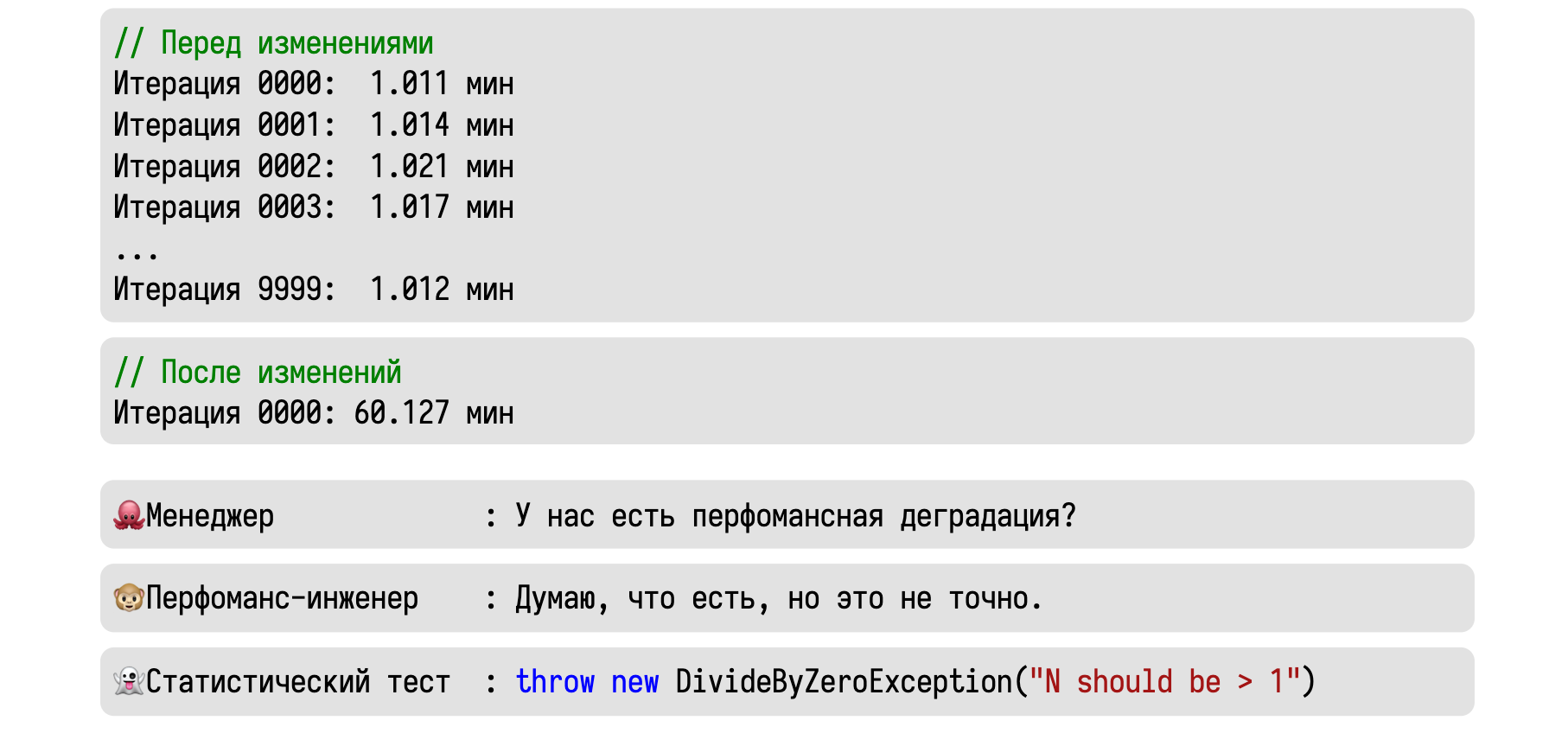
Давайте теперь попробуем использовать всё это на практике. Представим, что мы сделали 10000 итераций некоторого бенчмарка и стабильно получали значение около одной минуты.

Затем мы сделали некоторые изменения, выполнили одну итерацию и получили сразу 60 минут. Приходит менеджер и спрашивает, есть ли у нас тут перформанс-деградация.

Вменяемый инженер скажет, что скорее всего есть, но уверенности в этом нет.
Это мог быть единичный случай какого-то хитрого рейса, в результате которого всё зависло.

А статистический тест вообще ничего не скажет. Основная часть тестов считает дисперсию, которую нельзя подсчитать при наличии единственного замера.

Давайте попробуем ещё раз. Начальные условия те же: 10000 итераций по одной минуте. После изменений в исходном коде мы выполнили три итерации, каждая из которых заняла час. Теперь, если менеджер спросит о том, есть ли у нас деградация, то хороший инженер ответит, что скорее всего есть.

Крайне маловероятно, что наш чудо-рейс не проявлял себя 10000 раз, а потом внезапно стрельнул три раза подряд. Стоит поизучать этот феномен и разобраться, куда же ушёл целый час. А статистический тест скажет нам, что нельзя отвергнуть нулевую гипотезу.

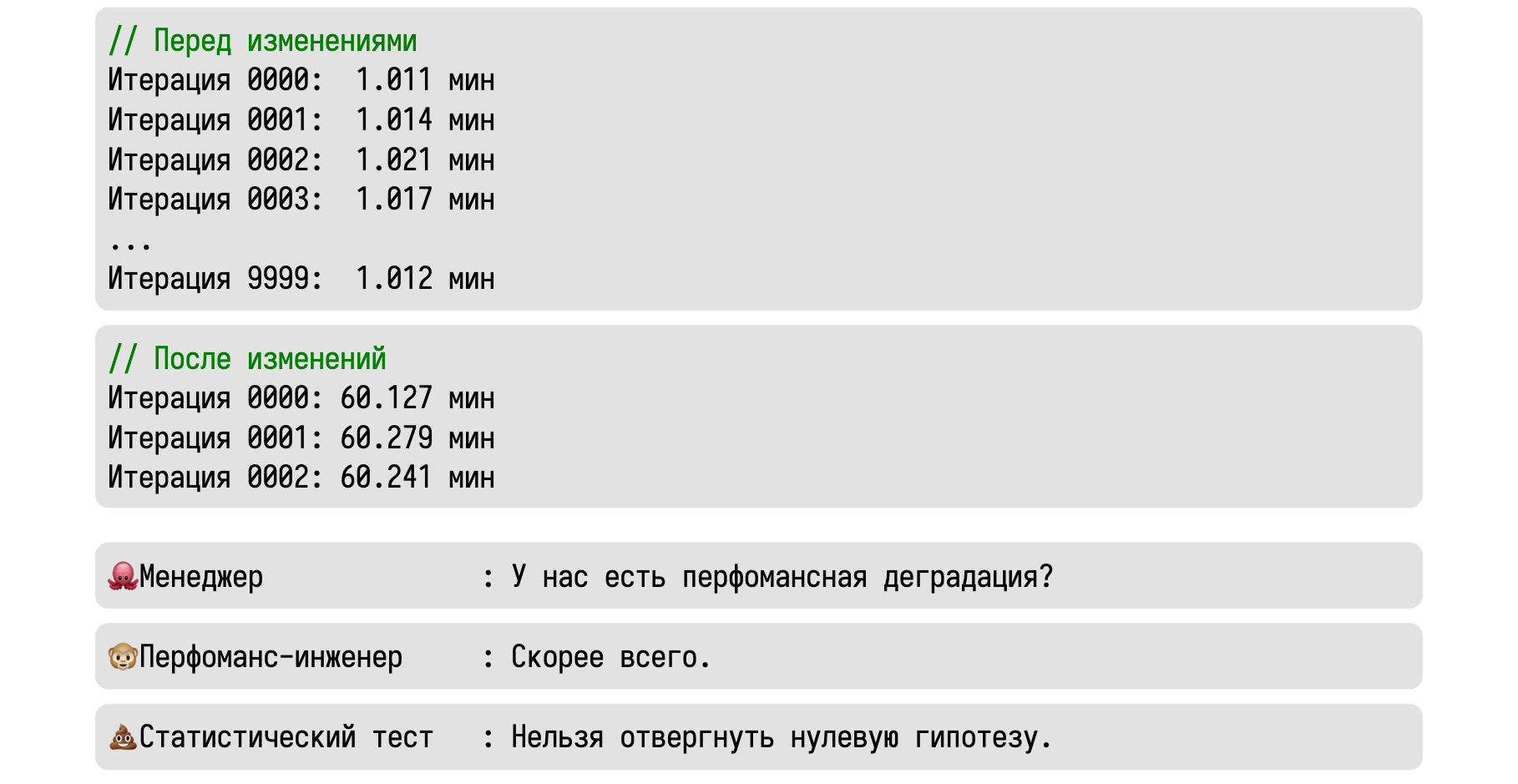
Многие думают, что этим он на самом деле хочет сказать, что деградации нет. Но в действительности он хочет сказать, что у нас недостаточно данных, чтобы обнаружить статистически значимую разницу. В статистике есть ещё одно магическое число: 30. Утверждается, что нам нужно сделать 30 итераций, чтобы чего-то значимое обнаружить. Но, согласитесь, глупо ждать 30 часов, чтобы убедиться в наличии проблемы. Да, в данной ситуации с тремя замерами мы не можем обнаружить статистически значимую разницу. Но мы можем обнаружить практически значимую разницу. А это намного важнее.

Ещё один пример: представьте, что вы добавили проверку на null в одном из методов.
Вы уверены, что null никогда не придёт, но на всякий случай решили это проверить.

Получаем стандартный вопрос от менеджера о том, есть ли у нас деградация. Нормальный инженер разумно рассудит, что мы добавили нового кода, а этот код занимает какое-то время. Значит, наш метод должен работать немного дольше.

А статистический тест опять нам скажет, что нельзя отвергнуть нулевую гипотезу.
На самом деле, в теории, если мы сделаем очень много итераций, то разницу можно будет и обнаружить. Но делать мы так, конечно, не будем.

В итоге получаем ситуацию, что вне зависимости от наличия или отсутствия маленькой деградации, статистический тест будет что-то бормотать про невозможность отвергания нулевой гипотезы. Бессмысленный результат, от которого довольно мало толка. А проблема в том, что мы совершили ошибку третьего рода: мы изначально задали неправильный вопрос.

Давайте попробуем ещё раз. Хороший менеджер должен был спросить, насколько велика деградация. Программисты каждый день пишут новый код и повсеместно вносят сотни деградаций в разные места. И это нормально. На практике мы не должны волноваться о всех деградациях, нас интересуют только самые большие деградации.

Хороший инженер скажет, что деградация очень маленькая, можно не волноваться.
Если бы мы сделали очень много итераций, то могли бы тут обнаружить статистически значимую разницу. Но вот только практически значимая разница бы всё равно не появилась. А вот статистические тесты на такой вопрос отвечать совсем не умеют, не эту задачу они решают.

В завершение этого раздела мне хотелось бы рассказать одну историю про использование p-value, за которую группа очень умных исследователей получила почётную награду по неврологии. Они занимались функциональной магнитно-резонансной томографией и решили провести следующий эксперимент. Подопытному показывали фотографии людей и спрашивали у него, какие по его мнению эмоции испытывают люди на фотографиях. Наборы фотографий показывались по 10 секунд, после чего подопытному давали 12 секунд на отдых. Общая продолжительность эксперимента составила почти 6 минут.

Полученные снимки фМРТ были проанализированы с помощью статистических тестов с пороговым значением для p-value 0,001, в результате чего были определены фотографии, которые вызывали определённые реакции в мозге. И это было бы абсолютно типичным исследованием, но вот только подопытным был… мёртвый атлантический лосось.

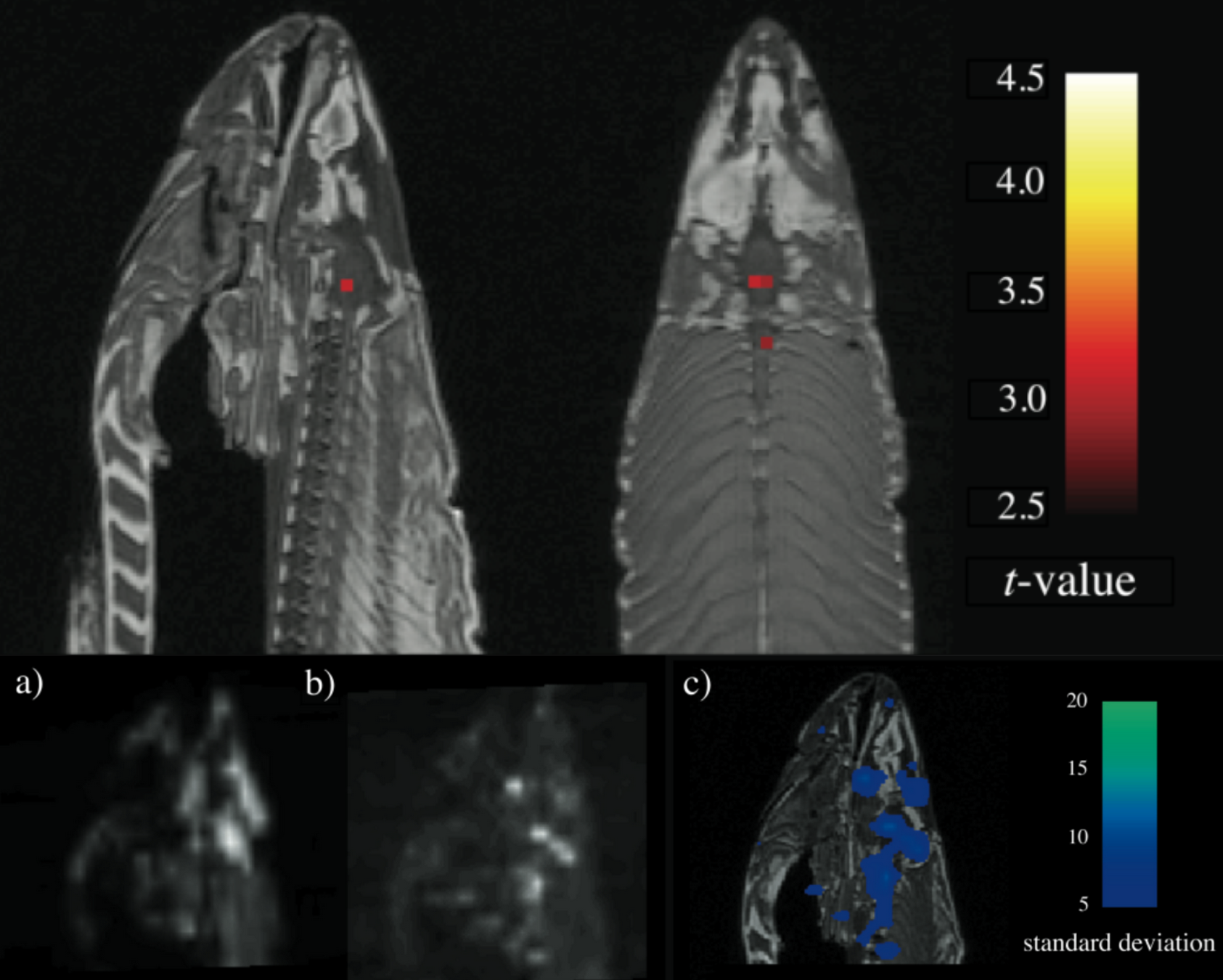
Всего за 6 минут учёные получили статистический значимый результат, который заключался в том, что у дохлой рыбы есть мозговая активность. А почётной наградой была Шнобелевская премия.

Резюмируем:

• Cтатистические тесты сложны для восприятия и использования.
• Они обладают множеством скрытых ограничений.
• У них всё очень плохо с воспроизводимостью.
• Они отвечают не на тот вопрос, на который мы хотим ответить.

Если вам неохота во всё это вникать, то можете просто запомнить, что статистические тесты просто не нужны в перформанс-анализе. Сразу хочу сказать, что это моё личное мнение, есть большое количество умных учёных, которые со мной не согласны.

Тут нужно понимать, что мы не говорим о том, что статистические тесты работают неправильно. Они хорошо решают ту задачу, для которой они создавались. Иногда они в каком-то виде могут решить вашу задачу и выдать более или менее вменяемые результаты. Но вот только в реальной жизни чаще всего можно использовать другие подходы, которые намного лучше справятся с вашими задачами.

Но довольно про плохие подходы. Давайте поговорим о хороших подходах, с помощью которых можно получить полезную информацию.

4. Сравниваем перформансные распределения

Как сравнить два распределения и не наступить на грабли? Методов великое множество. В целом, я рекомендую смотреть в стороны байесовской статистики и функций правдоподобия. В качестве метрик лучше всего использовать оценки на конкретные точки или, что ещё лучше, на интервалы. Мы не будем обсуждать все возможные варианты оценок, их слишком много. Вместо этого я расскажу о том, что я использую на практике для решения повседневных реальных проблем.

Начнём с анализа того, что у нас может пойти не так. В простейшем случае при внесении изменений в исходный код, всё распределение целиком может сдвинуться.

Если у нас имеется эффект мультимодальности, а он довольно часто возникает в перформанс-мире, то сдвинуться может только одна мода.

А может получиться так, что сдвигаются две моды, причём в разные стороны. То есть после изменений в части случаев мы начинаем работать быстрее, а в другой части — медленнее — типичная ситуация для изменения трейдофов.

Анализировать подобные проблемы нам поможет функция сдвига. Строится она довольно просто.

Представьте, что у вас есть два распределения. Разделим первое распределение на четыре части, в каждой из которых будет присутствовать ровно четверть ваших замеров. Точки, разделяющие такие части, называются квартилями.

Аналогичную процедуру повторим со вторым распределением. Далее нужно подсчитать разницу между соответствующими квартилями в первом и втором распределении. Можно подсчитать на сколько у нас уехал первый, второй и третий квартиль.

Распределение можно разрезать не на четыре части, а на произвольное количество частей. Общее название для точек разделения частей — квантили.

Если разделить распределение на очень-очень много частей и подсчитать сдвиг для каждого квантиля, то получим функцию сдвига. Она для каждого числа от нуля до единицы говорит, как сдвинулся соответствующий квантиль.

На первой картинке вы видите функцию сдвига для всего распределения. Легко понять, что тут происходит: для каждого квантиля сдвиг оказался положительным, все квантили уехали на тридцать условных попугаев вправо. На второй картинке процентов 70 распределения осталось на месте, а оставшиеся 30% сдвинулись. Это соответствует сдвигу одной моды. А на третьей картинке мы видим сдвиг двух мод. Одна часть распределения уехала влево, то есть ускорилась, а другая часть уехала вправо, то есть замедлилась.

По аналогии можно построить функцию пропорции. Её отличие в том, что вместо абсолютной разницы мы считаем отношение между соответствующими квантилями.
Функция пропорции показывает, на сколько процентов изменился каждый фрагмент распределения.

Функции сдвига и пропорции помогают быстро понять, что произошло. На данной картинке вы видите тримодальное распределение, у которого сдвинулась средняя мода. Обычные сводные метрики вроде среднего значения или дисперсии могут почти не измениться при такой трансформации. Но функция сдвига мгновенно показывает нам суть изменений.

Ссылка для тех, кто хочет рассмотреть более детально

А тут у нас творится какое-то непотребство: распределениям стало очень плохо. Даже глядя на графики распределений, сложно сказать, что именно поменялось. Функция сдвига опять оказывается очень удачной визуализации. Если говорить о конкретных способах подсчёта, то у нас есть очень много разных подходов. Есть разные алгоритмы для построения функции плотности распределения и для подсчёта квантилей.

Для маленьких выборок у функции сдвига нужно откидывать крайние значения, чтобы получить воспроизводимый результат. Для точек функции сдвига можно также оценивать доверительные интервалы, для расчёта которых тоже есть разные способы. Например, можно использовать обычный бутстрап, чтобы улучшить точность оценок. А ещё все значения функции можно свернуть в интервал, который будет оценивать минимальное и максимальное значение функции.

Все это заслуживает отдельного доклада, поэтому опустим обсуждение технических деталей реализации и продолжим говорить в целом про подход.

На графики смотреть не очень удобно, поэтому было бы здорово обобщать большое количество экспериментов в виде таблички. На данном примере у нас есть метод A, который мы считаем эталонным. Метод B работает в 1,5–3 раза медленнее, чем метод A. Для метода C пропорция составляет 1,2–1,4 раза, а для метода D — 1,2–1,3 раза.
Не нужно помнить определения сложных статистических метрик, чтобы понять происходящее.

Представьте, что мы заменили метод A на методы B, C, D на разных продакшн-серверах — и наши бенчмарки показали деградации. Тут можно получить разумный вопрос от менеджера о том, действительно ли у нас есть все эти деградации. У нас же довольно мало данных в таблице, это может быть просто случайный шум.

Мы можем ожидать ответа от нашего инженера вида: «В случаях B и C деградация скорее всего есть, там собрано много данных». А для метода D инженер может сказать: «Ну, тут непонятно, данных мало, надо бы собрать ещё замеров». И это именно тот ответ, который хочет получить менеджер, так как понятно, что с ним делать.
В случаях B и C надо разбираться, что произошло, а в случае D нужно сделать ещё замеры.Приятный контраст со странным предложениями про нулевые гипотезы, с которым совершенно непонятно, что делать.

А знаете что? Нам не обязательно беспокоить нашего инженера каждый раз, и такие штуки тоже можно автоматизировать.

Мы же знаем нашу предметную область, мы знаем бизнес-требования к производительности. Вполне можно написать простые проверки, которые ответят на наш вопрос без привлечения человеческих ресурсов.

Я бы мог ещё несколько часов рассказывать про хитрые математические нюансы, но мне хотелось, чтобы вы просто запомнили одну вещь. Самое главное — задать правильный вопрос. Вместо поиска каких-то абстрактных деградаций неизвестного размера нужно концентрироваться на том, насколько большие деградации у нас имеются. Если вопрос правильный, то нужные алгоритмы можно подобрать по ходу работы. А если использовать подход с дружелюбной статистикой, то будет вообще хорошо.

5. Анализируем историю замеров

Настало время перейти к третьей задаче перформанс-анализа и поговорить о том, как правильно работать с историей замеров. Прежде всего нужно понять, что характер изменений может быть очень разным.

Представьте, что у нас есть бенчмарк с фиксированным распределением. В какой-то момент происходит небольшая деградация, но вместо со сдвигом всего распределения меняется его форма. Потом происходит ещё одна большая деградация с очередным изменением формы.

После этого начинает расти разброс значений. Среднее значение и медиана остались на месте, а дисперсия увеличилась.

А потом наше распределение внезапно становится бимодальным. И тут уже сложно сказать деградация ли это или ускорение, но что-то важное определённо поменялось. А потом распределение и вовсе становится тримодальным.

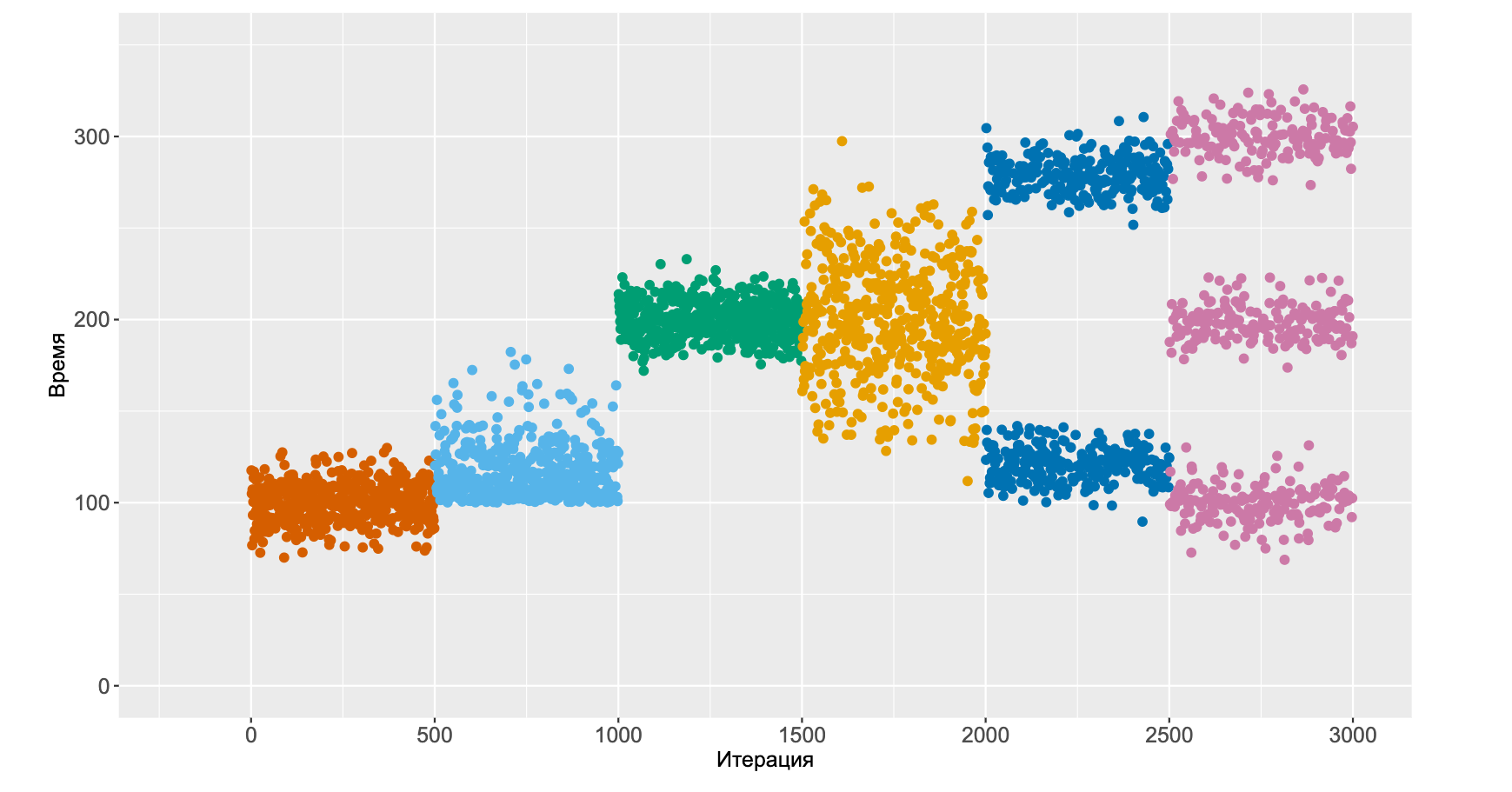
Описать такое в терминах деградаций довольно сложно.
Можно лишь сказать, что что-то поменялось, и это изменение выглядит довольно важным.

Точки, в которых что-то такое происходит, в русской литературе называются точками разладки. В английской литературе есть более удачный термин — changepoints.

Для обнаружения точек разладки есть очень много разных алгоритмов. Сейчас вы видите довольно неплохую сводную таблицу из одной хорошей статьи, последняя ревизия которой публиковалась несколько месяцев назад. С этой статьи хорошо начать ознакомление с этим замечательным разделом математики. Но мы будем обсуждать только то, что хорошо работает на практике и быстро выдаёт надёжные результаты на перформанс-данных.

Из всех представленных методов мне больше всего понравился алгоритм ED-PELT из статьи 2017 года. У него неплохая точность при адекватной скорости работы. Точную асимптотику оценить сложно, но она явно быстрее, чем O(n2).

Идея алгоритма базируется на динамическом программировании. Положим, у нас есть некоторая история замеров. Каждому замеру мы сопоставляем некоторую стоимость, которая говорит нам о том, насколько удачно мы можем найти точки разладки на участке истории от начала и до текущего замера. Также у нас есть обратные рёбра, которые указывают на предыдущую точку разладки в предположении, что текущий замер является последним. Положим, что мы подсчитали стоимость и обратные рёбра для некоторого количества замеров, но тут появляется новый замер.

Мы перебираем всех возможных кандидатов на предыдущую точку разладки.

Для каждого такого ребра можно оценить его стоимость, которая будет показывать, насколько удачен такой вариант разбиения. Ну и применяем стандартную формулу динамического программирования, которая позволяет оценить оптимальную стоимость для нового замера. Предыдущая точка разладки, в которой обнаружился минимум, позволяет нам определить обратное ребро.

Ура, мы подсчитали новую стоимость!

Если текущий замер действительно является последним в нашей истории, то пройдя по обратным рёбрам, можно восстановить все точки разладки. Алгоритм довольно прост, но вот только его сложность O(N²). Тут нам поможет подход под названием PELT, про который можно почитать в статье 2012 года.

Он предлагает довольно простую эвристику: мы можем по ходу выполнения алгоритма перебирать не все возможные предыдущие точки разладки, а только некоторую часть.
На реальных данных можно обнаружить довольно много предыдущих точек, про которые можно сразу сказать, что они не помогут нам минимизировать функцию стоимости. Эта эвристика помогает в разы ускорить алгоритм поиска точек разладки и очень быстро получить результаты даже на большой истории.

Функция стоимости на эмпирическом распределении

Остаётся только вопрос с тем, как выбрать функцию стоимости. Давайте быстро взглянем на основные формулы.

Обозначим множество замеров буквой x, а индексы точек разладки — буквой τ.

Далее введём эмпирическую функцию распределения, которая для каждой пары соседних точек разладки сопоставит значению t количество замеров на соответствующем интервале, которые этот t не превышают.

После этого можно выписать непараметрическую функцию максимального правдоподобия. Можно сказать, что для каждого участка между точками разладки она определяет степень его гомогенности.

Далее довольно хитрым способом считаются позиции некоторых квантилей, которые мы будем брать из распределения, основанного вообще на всех замеров из нашей истории. Нам также понадобится ввести штраф на появление новых точек разладки.
Без штрафа мы можем объявить, что абсолютно все замеры являются разладками, а это не совсем то, что нам хочется. В итоге мы получаем красивую формулу стоимости ребра. Она суммирует оценки гомогенности покрываемого участка истории по всем квантилям с помощью функции правдоподобия и добавляет к этому наш штраф.

Если вы ничего не поняли, то это нормально. Мне потребовалось перечитать статью раз 7, чтобы разобраться во всех тонкостях. Я показал эти формулы только затем, чтобы у вас появилось общее представление и в голове остались ключевые слова, которые могут помочь при поиске и анализе разных алгоритмов поиска разладок, если вы решите углубиться в эту область.

Самое главное, что этот алгоритм работает. И работает довольно неплохо. Особенно если у вас не очень много точек разладки.

Но есть проблема: функция стоимости основана на квантилях из полного распределения всех наших точек. Это приводит к тому, что при наличии большого количества разладок алгоритм будет их систематически пропускать.

Если мы хотим анализировать истории замеров за несколько месяцев, то такой пропуск важных разладок может быть не очень приемлемым.

Давайте попробуем придумать другую функцию стоимости! Пусть у нас есть два распределения. Для удобства разведём их по оси ординат. Найдём интервал, на котором распределения пересекаются. Далее подсчитаем, какой процент занимает интервал пересечения от интервалов каждого из распределений. Перемножив эти два числа, мы и получим новую функцию стоимости.

Давайте посмотрим, как такая метрика работает в различных случаях.

Если распределения не пересекаются, то метрика равна нулю. А если они совпадают, то метрика равна единице. Если же одно распределение занимает половину от другого распределения, то метрика равна 0,5. А если интервал пересечения занимает половину от каждого из распределений, то метрика равна 0,25.

Подход довольно интересный, но вот только он не учитывает форму распределения.
Результат может быть легко испорчен наличием нескольких больших выбросов. Но есть способ улучшить наши вычисления.

(Если вы обратили внимание на то, что площади десятипроцентных сегментов на этом графике не совсем совпадают, то подробнее об этом можно почитать тут.)

Для этого нужно разрезать каждое распределение на части. Например, с помощью децилей мы можем его разделить на десять равных частей. После этого можно применить ту же формулу для каждой пары децильных отрезков, просуммировав их с разными весами. С выбором этих весов можно экспериментировать, но прямо сейчас мы не будем углубляться в детали подбора коэффициентов. Это не особо увлекательно. Вместо этого попытаемся ответить на более интересный вопрос о том, как же нам быстро подсчитать значение квантилей на заданном отрезке.

И в этом нам поможет структура данных под названием Range Quantile Queries или RQQ. Она основана на сбалансированных вейвлет-деревьях. Это может звучать не очень понятно, поэтому давайте быстренько посмотрим на то, как такие деревья строятся.

Допустим у нас есть некоторый массив чисел. Весь массив целиком будет корнем нашего дерева. Найдём в нём медиану и покрасим элементы массива в два цвета.
Один цвет для чисел, которые меньше медианы, а другой — для чисел, которые больше медианы. Под первыми напишем букву L, а под вторыми — букву R. Эти буквы подскажут нам, куда попадёт каждый из элементов текущего узла. Элементы с буквой L попадут в левого ребёнка корня, а с буквой R — в правого. Далее мы повторяем процедуру для дочерних узлов, разделяя числа в каждом узле по соответствующей медиане. По аналогии строим третий уровень дерева и повторяем процедуру для новых узлов. Узлы, в которых оказался один элемент, становятся листьями дерева, а к остальным мы продолжаем применять нашу процедуру разделения по медиане. В итоге приходим к состоянию, когда каждое из чисел оригинального массива оказалось в одном из листьев. Ура, наше дерево готово!

Как мы видим, на уровне листьев мы получили отсортированную версию массива. Данная структура данных строится один раз за O(N*log(N)) и позволяет за O(log(N)) получить значение заданного квантиля на заданном отрезке. Попробуйте на досуге самостоятельно додумать, как именно делается такая операция. Если не получится, то можно подсмотреть в оригинальной статье, там всё довольно неплохо расписано.

Без Rqq для получения значения квантиля на отрезке нам бы пришлось каждый раз сортировать каждый отрезок, что значительно ухудшило бы производительность алгоритма в целом. А с использованием Rqq всё считается довольно быстро.
Назовём новый алгоритм поиска разладок RqqPelt.

Работает он немного дольше по сравнению с EdPelt, но зато он способен находить все точки разладки даже на большой истории. Мы уже несколько месяцев гоняем RqqPelt в Rider на наших наборах тестов и он показывает очень хорошие результаты. Надо признаться, что есть небольшой процент false positives, но зато мы ещё ни разу не пропустили ни одной важной разладки.

Как начать это использовать?

Звучит это довольно сложно, но для начала использования подобных алгоритмов не нужно вникать во всю математику.

Просто попробуйте

Для начала лучше всего просто попробовать эти алгоритмы на вашем проекте и посмотреть, есть ли от него польза. Автор алгоритма EdPelt сделал пакет на языке R со своим алгоритмом. В Perfolizer я добавил реализацию как EdPelt, так и RqqPelt.
Можете попробовать использовать его через NuGet-пакет или просто из командной строки. Интерфейс предельно простой: вы даёте на вход историю замеров, а на выходе получаете индексы точек разладки.

Анализируйте ограничения

Если окажется, что на вашем проекте от подобного подхода есть польза, то дальше можно заняться анализом ограничений.

Вам нужно подумать о нескольких вещах:

• Сколько у вас тестов? Можно работать с дюжиной выверенных бенчмарков, а можно попытаться анализировать все несколько сотен тысяч тестов, которые у вас есть.
• Сколько замеров на каждый тест вы можете себе позволить? Можно пытаться работать с одним замером в день, а можно делать сотни замеров в день.
• Какой масштаб изменений вы хотите обнаруживать? Некоторых устроит, если они будут находить деградации от 100%, а кому-то очень важно находить даже 5-процентные деградации.
• Сколько времени вы готовы потратить на поиск? Устроит ли вас, если обработка всей базы замеров будет занимать несколько часов или вы хотите получать результаты за несколько минут?

Зная все эти ограничения, вы можете подобрать оптимальный алгоритм конкретно для вашего проекта. К сожалению, универсальных алгоритмов, которые подходят абсолютно для всех проектов не существует. Но теперь у вас в голове есть самое главное: общее представление об подходах к поиску разладок и набор ключевых слов. Этого вполне достаточно, чтобы начать изучать тему и подобрать решение, которое в ваших условиях принесёт максимальную пользу.

История про медленный NuGet-сервер

В завершение раздела хочется рассказать ещё одну из моих любимых историй.

В Rider у нас есть набор тестов, которые покрывают функциональность нашего пакетного менеджера. В том числе, они работают с официальным репозиторием пакетов nuget.org. За производительностью этих тестов мы методично следим.

Перенесёмся в май 2018 года. Система мониторинга уже развернута, у нас есть красивые графики и автоматические алерты. Графики показывают идеальные результаты, каждый тест проходит за две-три секунды. Так продолжается некоторое время… Четвёртого мая мы обнаруживаем, что один из запусков занял 125 секунд. Он был всего один, поэтому мы решили пока ничего не делать и продолжить наблюдение.

Пятого мая у нас уже было два прогона по 125 секунд. За шестое мая мы получили четыре прогона по 125 секунд и один прогон на 250 секунд. Седьмого мая мы поняли, что ситуация становится очень грустной и с ней нужно разбираться.
Написать репро не составило труда, и мы быстро нашли проблему.

Некоторый процент оригинальных TLS1.2-запросов к нугетному серверу подвисал и падал по таймауту через две минуты, после чего происходил даунгрейд на TLS1.1 и повторный запрос. Какой-то процент повторных запросов тоже отваливался по таймауту через две минуты. Далее происходил даунгрейд на TLS1.0 и ещё один уже третий запрос. Какой-то процент из этих запросов тоже таймаутился, но дальше даунгредиться было некуда, поэтому запрос падал и ничего не возвращал.

Проблема была на стороне нугетного сервера, поэтомы мы написали об этом в Microsoft, и они быстренько всё починили. Самое важное в этой истории то, что у нас был анализ истории и мультимодальности распределений, поэтому мы мгновенно нашли проблему. Судя по всему, на стороне Microsoft такого анализа не было, или он работал не особо хорошо.

В результате у них появилась реальная продуктовая проблема, которая влияла на пользователей всех .NET IDE, включая их собственную Visual Studio. Обнаружить и локализовать подобную проблему без автоматизированной аналитики очень-очень сложно. Мораль: анализировать историю полезно.

На вашем CI-сервере или продакшн-сервере уже наверняка есть много полезных данных. Потратив немного усилий, можно добавить к ним очень мощную аналитику и бесплатно узнавать о важных перформанс-проблемах максимально оперативно. Это позволит починить данные проблемы до того, как пользователи начнут на них жаловаться.

6. Анализируем точки разладки

Однако после первой попытки реализовать поиск точек разладки, вы можете столкнуться с ситуацией, когда этих точек очень много. И просмотреть их все вручную не получится. Что же делать?

Давайте вкратце поговорим об анализе уже найденных разладок. Самый эффективный подход предельно прост. Разбиваем историю по точкам разладки. Для каждой пары соседних участков истории считаем функцию сдвига или функцию пропорции. Превращаем эти функции в интервалы и сортируем по ним тесты. В полученной сводной таблице мы увидим самые критичные проблемы на самом верху.

Тут тоже есть определённый процент ложных результатов. Но самое главное, что в реальной жизни основная часть критичных проблем очень быстро попадает вверх такой таблице.

Можно строить такие таблицы не только по точкам разладки, но и по распределениям на отдельных участках истории.

Я очень люблю сортировать распределения по дисперсии. В тестах с большим разбросом по перформанс-замерам зачастую можно встретить много продуктовых проблем.

А ещё можно сортировать тесты по мультимодальности. Если в распределении несколько чётко выраженных мод, то это также может оказаться плохим симптомом.

Для многих клиент-серверных проектов важно смотреть не только на медианное время, но и на процентили. Много полезного можно обнаружить, отсортировав распределения по 95-му или 99-му процентилям. Учтите, что у вас должно быть достаточное количество замеров, чтобы корректно вычислить эти процентили.

А ещё можно сортировать распределения по наличию экстремально больших замеров.

Я вам рассказал про свои любимые метрики для сортировки, но вы можете придумать свои метрики, которые подходят под бизнес-требования в вашем конкретном проекте.

В теории всё это может звучать довольно здорово. Но, как говорил Йоги Берра, в теории между теорией и практикой разницы быть не должно, хотя на практике она есть.

Ищем разладки в реальной жизни

Давайте посмотрим как всё это работает в реальной жизни.
Перенесёмся в 4 ноября 2019 года, понедельник. Мы только что развернули новый алгоритм поиска разладок и начали следить за графиками. Для начала мы начали смотреть за билд-конфигурациями с самыми обычными юнит-тестами, которые запускались на виртуальных агентах. Пять дней всё было довольно неплохо.

В субботу наши тесты начали внезапно ходить немного быстрее. У нас были настроены алерты на все точки разладки, поэтому мы сразу об этом узнали. Порадовались, что кто-то, видимо, что-то прооптимизировал, перформанс улучшился, мы об этом узнали — красота.

Но вот только в понедельник случилась деградация и перформанс вернулся на прежний уровень. Скорость работы по сравнению с прошлой неделей не уменьшилась, поэтому мы решили пока что ничего не делать.

Но на следующих выходных ситуация повторилась. Мы немного подумали и догадались, в чем причина. По будням нагрузка на билд-сервер довольно большая: ресурсов мало, тесты ходят долго. По выходным часть сотрудников перестаёт работать, нагрузка падает, ресурсы освобождаются, тесты начинают ходить быстрее.

Вроде бы всё разумно, но вот наш алгоритм поиска разладок жизнь к такому не готовила. Захотелось избавиться от подобных систематических уведомлениях о ложных разладках.

Учитывая периодическую природу возникновения разладок, мы решили применить быстрое преобразование Фурье, перевести наши замеры в частотную плоскость, разложить его по гармоникам, выделить доминантные колебания, удалить их из оригинального сигнала, применить обратное преобразование Фурье, и только после этого запустить алгоритм поиска разладок на очищенном временном ряде. Мы довольно быстро реализовали это решение и избавились от ложных нотификациях по субботам и понедельникам. (Реализация показана на скриншоте выше)

Следующие три дня всё было хорошо. Но в среду вечером всем разработчикам пришло сообщение, что в мы начинаем готовиться к релизу и в понедельник будет feature freeze.

Все сразу начали запускать много билдов на сервере. Нашим графикам стало не очень хорошо. Преобразование Фурье больше не спасало, поэтому мы решили разобраться в проблеме детально.

Смотрим на железо

Давайте посмотрим на железо, на котором крутятся наши тесты.

У нас в серверной стоит хорошее интеловское ведёрко. Внутри находится два Xeon-процессора, на каждом 22 физических ядра.

На ведёрко приходится 19 виртуальных агентов, каждый из которых получает два физических ядра. Вроде бы особых проблем с ресурсами процессора быть не должно.

Но вот только все агенты используют общий SSD-диск — именно он и может оказаться проблемой.

Строим модель нагрузки

Мы решили построить модель нагрузки и написали бенчмарк, который активно читал с диска и писал на диск большие объёмы данных. Далее мы подготовили окружение для запуска этого бенчмарка в параллель на нескольких агентах и начали следить за временем их исполнения.

При запуске бенчмарка на одном агенте время его работы составило примерно 4,5 минуты. При запуске двух бенчмарков на двух параллельных агентах мы получили примерно 5,5 минут в каждом случае. На трёх агентах мы получили примерно 7 минут на бенчмарк.

Постепенно увеличивая нагрузку, мы пришли к тому, что при 19 параллельно запущенных дисковых бенчмарках мы получаем 33 минуты на каждый запуск.
То есть время бенчмарка может плавать от 4 до 33 минут в зависимости от общей нагрузки на сервер.

Глядя на этот график, многие мои коллеги говорят мне, что нельзя анализировать замеры в такой ситуации. А я всегда отвечаю, что мне никто не может запретить анализировать замеры. Действительно, не очень просто находить настоящие продуктовые проблемы при таком разбросе значений. Но иметь большой разброс — это нормально в перформанс анализе, мы должны учиться работать с такими данными. Сложности только делают задачу интереснее.

Мы ввинтили некоторое количество костылей в нашу логику анализов, и она успешно работает. А для написания костылей мы использовали построенную модель нагрузки: учёт количества единовременно работающих виртуальных агентов позволяет отнормировать результаты замеров.

Есть некоторый процент ложноположительных результатов, но я трачу на их просмотр не более двух-трёх минут в день. Зато мы каждый месяц успешно находим несколько довольно критичных реальных перформанс-проблем благодаря этой системе.

А достигается успех с помощью аккуратной сортировки всех точек разладки по разным критериям и учётом особенности наших агентов. Если бы мы использовали магические числа и посылали бы нотификации в случаях, когда время теста превысило бы заданную константу, то пользоваться системой было бы очень сложно.

Наличие волшебной сортировки сделало наши анализы действительно полезными.
В общем, не используйте магические числа — используйте сортировку.

7. Пишем перформансные тесты

Теперь пришло время разобраться с тем, как узнавать о деградациях не ретроспективно спустя какое-то время, а сразу. И помогут нам в этом перформанс-тесты!

В индустрии есть несколько распространённых подходов к написанию таких тестов. Самый простой — абсолютное условие. Мы просто падаем, если время теста превысило заданный таймаут. Этот способ очень плохой, так как он слишком зависит от железа, на котором исполняется тест.

Тут может появиться идея использовать относительное условие. Давайте введём некоторый эталонный бенчмарк и будем считать относительную производительность.

Если полученное число превышает заданное количество условных попугаев, то тест падает. Часть проблем с портабильностью бенчмарка данный подход действительно решает. Увы, любые источники шума, мультимодальность, выбросы и прочие эффекты быстро заставят этот тест мигать. Он будет падать просто так без реальных деградаций в исходном коде.

Как и в случае с разладками, нам поможет адаптивный подход. Можно написать бенчмарк следующим образом. Сначала мы загружаем историю замеров данного бенчмарка для данной конкретной машины. Далее мы делаем N итераций бенчмарка на текущей ревизии. И применяем хитрую математическую формулу, чтобы определить, есть ли у нас деградация. Ситуация стала лучше, но у нас всё ещё есть одна константа — количество итераций.

Можно сделать алгоритм ещё адаптивнее с помощью статистического последовательного анализа. Давайте рассмотрим этот подход с самого начала теста. Мы всё так же загружаем историю замеров. Далее делаем один-единственный замер на текущей ревизии. После этого задаёмся вопросом, есть ли у нас деградация.
Нужно помнить, что нас интересуют только значимые деградации, поэтому для каждого теста нужно заранее подумать о том, какого рода деградации нас будут интересовать. После того, как мы аккуратно определили целевые деградации, на заданный вопрос можно дать три разных ответа.

Можно сказать, что деградации нет — тест зелёный. Можно сказать, что деградация есть — тест красный. А можно сказать, что нам недостаточно данных для ответа на вопрос, нужно сделать больше замеров. И повторяем процесс до тех пор, пока не получим нужный результат.

Конечно, можно было бы сказать, что итераций много не бывает и делать их по 1000 штук каждый раз. Но тогда общая продолжительность запуска всех бенчмарков могла бы занимать часы, дни или даже месяцы. Тернарная логика позволит вам достичь оптимального соотношения между точностью перформанс-теста и временем его работы. Для логики проверки на деградацию стоит избегать использования статистических тестов.

Помимо уже рассмотренных проблем, сюда добавляется эффект под названием p-hacking. Вы не можете просто так добавлять в вашу выборку новые замеры и повторять тест. Это приведёт к значительному увеличению количества ошибок первого рода.
С этим можно бороться используя разные подходы вроде коррекции Холма-Бонферрони. При должном усердии можно заставить стат. тесты работать для такой задачи. Но на вашем пути будет множество подводных камней и соблазнительных возможностей выстрелить себе в ногу. Намного лучше использовать функции сдвига и пропорции.

Как принять решение?

Рассмотрим один пример на тему того, как можно реализовать логику принятия решений.

Построим некоторым образом кривую, задающее соотношение между размером деградации и количеством итераций, которые мы готовы совершить, чтобы эту деградацию обнаружить.

Делаем первую итерацию, считаем функцию пропорции, сжимаем её до одного числа, отмечаем точку на графике. Далее делаем вторую итерацию, обновляем значение функции пропорции, отмечаем точку на графике. Продолжаем процесс до тех пор, пока не встретимся с нашей волшебной линией.

В данном случае мы заранее договорились, что для обнаружения деградации на 100% нам достаточно 9 итераций. Подход выглядит костыльным и не очень математическим, но очень хорошо ложится на реальную жизнь. Математические формулы зачастую требуют от нас такого количества итераций, которое мы не можем себе позволить.
С помощью такой кривой мы можем заточить систему перформанс-тестов под наши конкретные требования.

Учтите, что это не готовый алгоритм, а только утрированное описание общего подхода — внутри большое количество пространства для творчества. Например, вы можете экспериментировать со способом превращения функции пропорции в одно число. Можете выбрать более сложную метрику для оси абсцисс. Проценты не всегда работают хорошо, так как не учитывают дисперсию. В случае нормальных распределений можно было бы использовать индекс d Коэна, но для перформанс-распределений нужно подбирать его непараметрические аналоги.

Приведённая кривая может быть не кривой, а хитрой комбинаций сложных условий.
Кривая символизирует собой наши бизнес-ограничения, которые мы часто забываем учитывать. Иногда мы просто не можем позволить себе такое количество итераций, которое требует от нас математика для получения статистически значимого результата. И это тоже нормально.

А что в реальной жизни?

Самое интересное в том, как приспособить этот подход к вашим бизнес-требованиям в реальной жизни.

Рассмотрим ещё один пример из райдерных тестов, в которых помимо общей продолжительности теста замеряются отдельные метрики.

Как мы видим, это сложный интеграционный тест, который занимает около пяти минут.
Но отдельные стадии этого теста могут занимать несколько секунд или даже доли секунды. При этом деградаций в этих отдельных стадиях мы тоже допускать не хотим.

Сравнивая два участка истории по общему времени работы целого теста, мы не видим каких-то очевидных проблем.

Но если посмотреть на первую метрику, то можно увидеть, что один-два раза на сотню итераций мы видим деградацию в десять раз. Препарирование логов показало, что проблема связана с хитрым рейсом, который в ближайшее время починить не получится. Приходится жить с такими феноменами на графиках и уметь их обрабатывать. В одной из первых версий логики перформанс-тестов мы предположили, что при возникновении десятикратной деградации можно падать после первой итерации. Увы, на данной метрике такой подход не работает, поэтому минимальное количество итераций для обнаружения проблемы поднялось до двух.

На второй метрике в какой-то момент распределение стало бимодальным. С вероятностью 1/2 мы наблюдаем двукратную деградацию. Учитывая, что общая продолжительность теста составляет 5 минут, мы решили, что мы не хотим делать больше 5 итераций. Ведь интеграционных тестов много, и мы хотим, чтобы они все проходили за разумное количество часов. Но в случае подобного феномена, один раз из 32 мы получаем ситуацию, когда все пять замеров второй метрики показывают деградацию, тест падает. К сожалению, побороться с такими проблемами в общем случае у нас так и не получилось.

Спасает адаптивная природа теста. Спустя пару дней ложных срабатываний, накапливается история, необходимая для переобучения теста. После этого он волшебным образом перестаёт падать.

В этом и вся прелесть адаптивного подхода, он справляется со многими проблемами сам без участия человека. После нескольких неудачных попыток нам удалось построить стабильную инфраструктуру для перформанс-тестов. Да, иногда бывают проблемы с ложным падениями, но их не так много. Зато мы пришли к состоянию, когда серьёзную деградацию физически невозможно вмёрджить в мастер-ветку.
Перформанс-тесты буду стабильно падать, и мёрдж не пройдёт. И это действительно работает. И вы тоже можете написать такую инфраструктуру для вашего проекта.

8. Допускаем ошибки

Должен признать, что всё это выглядит довольно сложным, с первого раза может не получиться. И тут стоит немного поговорить про ошибки. Да, техническая часть выглядит довольно сложной, но там нет ничего сверхсложного — со всеми алгоритмами вполне можно разобраться. Самые главные проблемы на пути к светлому перформансному будущему являются ментальными, они у вас в голове.

Для начала хочется рассказать историю про Томаса Уотсона-старшего — основателя корпорации IBM, который руководил ей больше 40 лет. В компании работал молодой топ-менеджер, который подавал большие надежды. Однажды он принял участие в рискованном проекте и потерял более 10 миллионов долларов — ужасная ситуация!
Нервничающий менеджер пришёл в кабинет к Уотсону и робко сказал: «Я думаю, вы хотите, чтобы я уволился?»

На что Уотсон ответил: «Вы шутите? Мы только что потратили на ваше обучение 10 млн долларов!» И это был блестящий ответ действительно грамотного руководителя.

Эту историю я прочитал в прекрасной книжке «Ошибки, которые были допущены (но не мной)». Она о том, насколько сложно обычному человеку признавать ошибки. В нашей культуре есть такой стереотип, что допускать ошибки — плохо. Если ты ошибся, значит ты тупой и неквалифицированный, тебя нужно уволить. А на самом деле, допускать ошибки — это круто! Это самый эффективный способ чему-то научиться.
Послушав доклад или прочитав книгу, вы можете обзавестись интересными идеями, но у вас не появится навыков. Действительно понять, как нужно что-то делать, можно только путём проб и ошибок. Чтобы процесс был эффективнее, могу дать вам пару советов.

Написание постмортемов. Если вы где-то облажались, то не пытайтесь скрыть свою ошибку и как можно скорее её забыть. Постарайтесь извлечь из неё максимум пользы. Проанализируйте ситуацию и поймите, что и где пошло не так. Подумайте, что нужно сделать, чтобы в будущем подобных проблем не возникало. В команде должна быть такая культура, чтобы процесс извлечения пользы из ошибок вызывал уважение.

Кросс-бенчмаркинг. Если вы работаете над какой-то оптимизацией в одиночку, то вам может быть сложно написать на неё нормальные бенчмарки. Психология так устроена, что вам может быть некомфортно искренне пытаться найти у себя проблемы.
Ведь если окажется, что вы всё сделали неправильно, то все скажут, что вы тупой, ведь вы сделали ошибку. В обычном тестировании считается нормальным, что один человек пишет код, а другой его тестирует. Но вот в перформанс-тестировании такая практика не очень распространена. Привлеките к перформанс-анализу коллег, которые помогут найти возможные ошибки. При таком подходе вы не только исправите ошибки на ранних стадиях, но и очень многому научитесь.

В ходе доклада некоторым могло показаться, что мне сразу было понятно, как решать те или иные задачи. Но я пришёл к этому знанию в процессе большого количества неудач. Я рассказал штук десять подходов, которые действительно работают на практике, но я могу рассказать ещё несколько сотен подходов, которые работать не будут.

Например, сегодня я много ругал статистические тесты. Но, должен признаться, я сам их активно использовал около пяти лет. И неоднократно рекомендовал их к использованию на докладах. Применять их в реальной жизни получалось плохо, но мне казалось, что просто со мной что-то не так. Ведь это индустриальный стандарт, много умных учёных их используют, и у них всё нормально.

А потом пришло озарение: что-то не так может быть с самими тестами. Я прочитал несколько дюжин статей критики статистических тестов и понял, что большая часть научного сообщества занимается какой-то ерундой. Люди не понимают, как правильно использовать инструмент, но журналы требуют написать в статье значение p-value, поэтому его приходится считать. Приходится p-хакать слишком большое значение p-value и описывать эвфемизмами вроде «почти значимый результат».

В итоге имеем десятки тысяч дурацких статей по медицине, биологии, психологии, физике и другим наукам в очень приличных журналах — отчасти потому, что людям некомфортно признавать ошибки.

Хочется рассказать ещё одну байку из книжки Талеба «Чёрный лебедь» про Карла Поппера — главного идеолога теории фальсифицируемости. Однажды у Карла Поппера спросили, можно ли «фальсифицировать фальсификацию». То есть можно ли проявить скептицизм по отношению к самой концепции скептицизма. Карл Поппер ответил, что выгонял студентов с лекций и за менее тупые вопросы.

Не уверен, что эта история произошла на самом деле, но она даёт хорошую пищу для размышлений.

В общем, развивайте критическое мышление, старайтесь во всём сомневаться и получайте удовольствие от собственных ошибок.

9. Читаем методическую литературу

Я сегодня рассказал про большое количество подходов для перформанс анализа, но не стал углубляться в технические детали реализации. Возможно, у некоторых из вас появилось желание всё-таки углубиться в данную тему и почитать умные книжки.

Увы, хорошая методическая литература конкретно про перформанс-анализ почти отсутствует. Дело в том, что это сложная дисциплина, которая сочетает множество других дисциплин. Поэтому я лишь могу порекомендовать разные хорошие книжки по смежным областям. Ни одна из них не сделает вас крутым перформанс-инженером, но комплексный взгляд на проблематику позволит вам выбрать верное направление и на собственном опыте всему научиться.

Кроме книжек также полезно читать разные научные работы. Искать статьи, в которых написано что-то адекватное и полезное, довольно сложно. Из-за исторически сложившейся монополии на рынке научных журналов, вы можете столкнуться с ситуацией, что некоторые статьи продаются за деньги. Небольшая заметка среднего качества легко может стоить 50 баксов.

Напоминаю, что пиратство — это плохо. Поэтому не нужно использовать сайт Sci-Hub, который позволяет мгновенно получить бесплатный доступ практически к любой публикации. В Twitter есть хороший совет на тему того, что не нужно добавлять на панель закладок скрипт, который дописывает sci-hub.tw к доменному имени. Ведь это позволит получить нелегальный доступ к бесценным знаниям вообще в один клик.

Помните, что учиться — это круто. Чем больше людей будет заниматься темой перформанс-анализа, тем быстрее наступит светлое будущее, в котором у нас есть хорошие проверенные инструменты для решения всех популярных задач.

10. Резюме

Вместо повторения названий всех алгоритмов мне хочется дать шесть советов для начинающих и опытных перформанс-инженеров.

Образовывайтесь в перформансной науке. Читайте умные книжки и статьи.

Анализируйте данные, которые у вас есть.
Не бывает плохих данных, бывают недоанализированные.

Адаптируйтесь к изменчивым и сложным перформанс-распределениям.
Не используйте магические константы, старайтесь писать адаптивные алгоритмы.

Сомневайтесь во всём и не доверяйте своей интуиции. Помните, что кошка Ося скорее всего окажется более квалифицированным перформанс-инженером, чем вы.

Думайте о том, почему мир устроен так, как он устроен. Если вы видите странный перформанс-эффект, то попытайтесь разобраться, почему он возник.

Ошибайтесь и делайте вывод из собственных ошибок. Это самый эффективный способ действительно чему-то научиться.

На самом деле эти советы подходят любым инженерам, вне зависимости от рода их деятельности. Подходы для решения сложных технических проблем базируются на одних и тех же идеях. Самые главные инструменты, с помощью которых вершится прогресс, это не какие-то фреймворки и алгоритмы, это критическое мышление и упорство. Вместе мы сможем оказаться в мире, где все программы работают быстро и никогда не тормозят!

11. Титры

Визуальное оформление

• Beamer theme gallery: Pittsburgh (Оформление слайдов)
• Okabe, Masataka, and Kei Ito. "Color universal design (cud)-how to make figures and presentations that are friendly to colorblind people." J Fly: Data Depository for Drosophila Researchers (2008).
  https://jfly.uni-koeln.de/color/
  (Цветовая палитра графиков, адаптированная для дальтоников)

Создание презентации

• remark: A simple, in-browser, markdown-driven slideshow tool (Движок для этой презентации)

Графики и иллюстрации

• Wickham, Hadley. "ggplot2." Wiley Interdisciplinary Reviews: Computational Statistics 3, no. 2 (2011): 180-185. (Графики)
• R package with functions for drawing density and frequency trail waterfall plots (Каскадные графики)
• Sketchviz (Блок-схемы)
• Grapholite: State-of-the-art diagrams editor for Desktop, iPad and Windows 10 tablets (Диаграммы)
• Adobe Illustrator (Иллюстрации)
• Paint.NET (Иллюстрации)

Основные шрифты

• Ubuntu Mono (Шрифт для текста)
• Iosevka (Шрифт для кода)
• Caveat (Шрифт для комиксов)
• Tinos (Шрифт для блок-схем)

Оборудование для эксперимента с термальным троттлингом

• MacBook Pro (Retina, 15-inch, Mid 2015, 2,5 GHz Quad-Core Intel Core i7, 16 GB 1600 MHz DDR3)
• Тепловентилятор керамический Vitek VT-2052
• Плед ИГАБРИТТА из IKEA
• Холодильник NEFF
• Тепловизор Seek Thermal Compact для Android

Используемые и упомянутые интернет-ресурсы

• https://en.wikipedia.org/
• https://getemoji.com/
• https://sci-hub.se/
• https://twitter.com/Protohedgehog/status/1005837592275881984

Источники фотографий

• Карл Поппер
• Томас Уотсон старший
• Craig M. Bennett
• Abigail A. Baird
• Michael B. Miller
• George L. Wolford
• Биткоины
  Photo by Thought Catalog on Unsplash

Вдохновение для иллюстраций

• Слайд "Типичный день перфоманс-инженера"
  Charmander the Firefighter
• Слайд "Кросс-бенчмаркинг"
  Инструкция по сборке IKEA

Библиография

Про способность находить закономерности:

• Tversky, Amos, and Daniel Kahneman. "Belief in the law of small numbers." Psychological bulletin 76, no. 2 (1971): 105.
• Панчин, Александр. "Апофения." СПб.: Питер, 2019. — 256 с. ISBN 978-5-4461-1086-5
• Taleb, Nassim. Fooled by randomness: The hidden role of chance in life and in the markets. Vol. 1. Random House Incorporated, 2005.

Про статистические тесты:

• Cohen, Jacob. "The earth is round (p<. 05)." In What if there were no significance tests?, pp. 69-82. Routledge, 2016.
• Amrhein, Valentin, Fränzi Korner-Nievergelt, and Tobias Roth. "The earth is flat (p> 0.05): significance thresholds and the crisis of unreplicable research." PeerJ 5 (2017): e3544.
• Wasserstein, Ronald L., Allen L. Schirm, and Nicole A. Lazar. "Moving to a world beyond “p< 0.05”." (2019): 1-19.
• Winder, W. C. "What you always wanted to know about testing but were afraid to ask." American dairy review (1973).
• Grieve, Andrew P. "How to test hypotheses if you must." Pharmaceutical statistics 14, no. 2 (2015): 139-150.
• Krawczyk, Michał. "The search for significance: a few peculiarities in the distribution of P values in experimental psychology literature." PloS one 10, no. 6 (2015).

Про cтатистический последовательный анализ:

• Lakens, Daniël. "Performing high‐powered studies efficiently with sequential analyses." European Journal of Social Psychology 44, no. 7 (2014): 701-710.

Про размер аффекта:

• Peng, Chao-Ying Joanne, and Li-Ting Chen. "Beyond Cohen's d: Alternative effect size measures for between-subject designs." The Journal of Experimental Education 82, no. 1 (2014): 22-50.
• Wilcox, Rand. "A Robust Nonparametric Measure of Effect Size Based on an Analog of Cohen's d, Plus Inferences About the Median of the Typical Difference." Journal of Modern Applied Statistical Methods 17, no. 2 (2019): 1.
• Tomczak, Maciej, and Ewa Tomczak. "The need to report effect size estimates revisited. An overview of some recommended measures of effect size." (2014).

Про функцию сдвига:

• Doksum, Kjell. "Empirical probability plots and statistical inference for nonlinear models in the two-sample case." The annals of statistics (1974): 267-277.
• Doksum, Kjell A., and Gerald L. Sievers. "Plotting with confidence: Graphical comparisons of two populations." Biometrika 63, no. 3 (1976): 421-434.
• Rousselet, Guillaume. "the shift function: a powerful tool to compare two entire distributions." 2016
• Rousselet, Guillaume. "Bayesian shift function." (2018)
• Akinshin, Andrey. "Distribution comparison via the shift and ratio functions." (2019)

Про разладку:

• Haynes, Kaylea, Paul Fearnhead, and Idris A. Eckley. "A computationally efficient nonparametric approach for changepoint detection." Statistics and Computing 27, no. 5 (2017): 1293-1305.
• Akinshin, Andrey. "Implementation of efficient algorithm for changepoint detection: ED-PELT." (2019)

Про k-й наименьший элемент:

• Gagie, Travis, Simon J. Puglisi, and Andrew Turpin. "Range quantile queries: Another virtue of wavelet trees." In International Symposium on String Processing and Information Retrieval, pp. 1-6. Springer, Berlin, Heidelberg, 2009.
• Alexandrescu, Andrei. "Fast deterministic selection." arXiv preprint arXiv:1606.00484 (2016).

Про квантильные оценки:

• Harrell, Frank E., and C. E. Davis. "A new distribution-free quantile estimator." Biometrika 69, no. 3 (1982): 635-640.

Раз этот хабрапост вас так заинтересовал, что вы добрались до конца — вероятно, вас заинтересует и конференция DotNext 2-5 декабря: там тоже будет много ценного контента для .NET-разработчиков.