С чего начать постройку дрона-дирижабля

Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!

Начинать следует с проектирования. Проектирования внутренней оболочки. Вернее сначала внешней, допустим мы её уже спроектировали и она выглядит так:

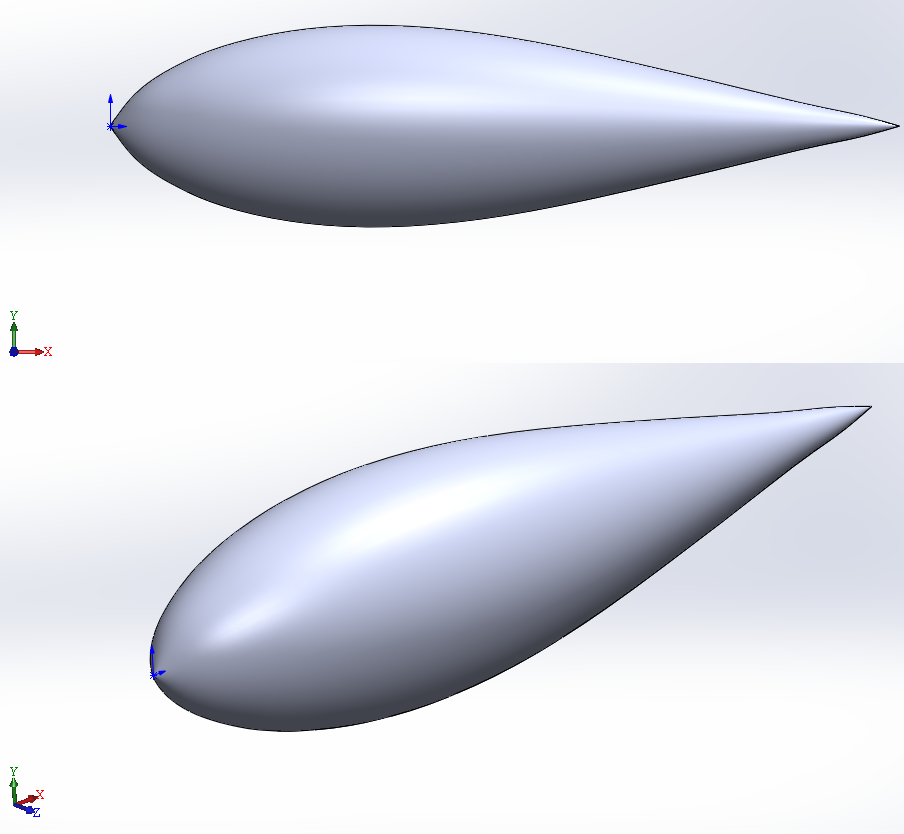
Тут её размер примерно 5 метров в длину и метр с чем-то в ширину (или толщину). Оболочка должна быть небольшой (ведь дрон - это дрон), главное достаточной для поднятия небольшого груза, эта поднимет 4 кг.

А, кстати, в реальности она может быть похожа на эту:

Рис. 2 - Оболочка в реальности (не та что на рисунке 1, другая, но это не важно, лишь для примера)

О, а тут я тестирую её =) :

Но сейчас не об этом, нужно спроектировать внутреннюю оболочку. Я её называю - пузырь... Внутренний пузырь дирижабля. Он нужен для того, чтобы дрон смог взлетать на высоту и приземлятся обратно. Еще он нужен для парирования погодных условий. Также он важен для того, чтобы поддерживать избыточное давления в дирижабле (тогда он становится твёрдый и хорошо держит форму). Сложно объяснить для чего нужен пузырь, это нужно увидеть своими глазами... Увидеть зависимость параметров атмосферы от высоты (кто не видел, конечно, сейчас покажу, секунду):

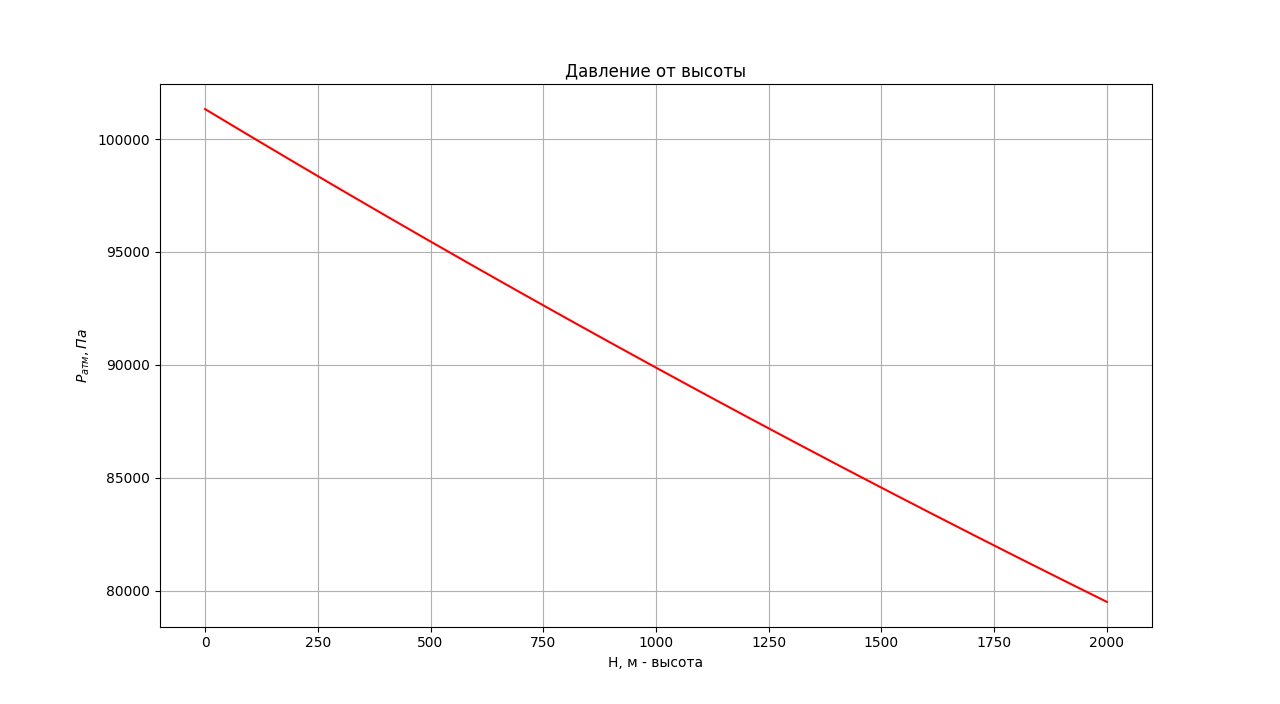
Рис. 4 - Параметры стандартной атмосферы

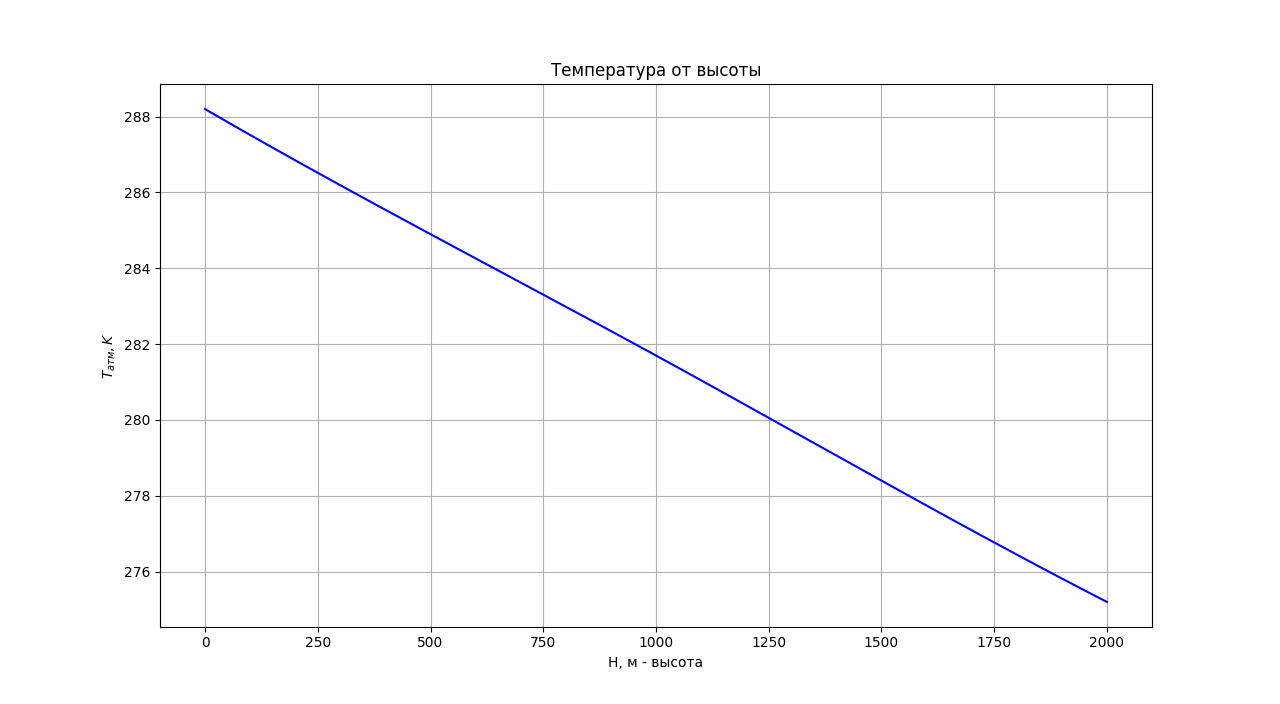
Они все падают, снижаются с высотой. А это значит, что если мы накачаем оболочку водородом на земле, внутри у неё будет давление немножко больше атмосферного. Но как только мы подымемся на высоту, оно станет больше наружного уже не немножко, а очень даже множко. Разница давлений вырастет, и оболочка раз и лопнет. Законы физики. Все шарики, которые люди запускают в праздники, поднимаются на некоторою высоту и лопаются. Они не летят в космос, и даже не путешествуют по планете стабилизировавшись на конечной высоте в ветряных потоках атмосферы. Потому нам нужен внутренний пузырь. Это будет отличать наш аппарат от стратостатов всяких и метеозондов, которые раздуваются с высотой до меняют свою форму. Наш дрон должен быть как дрон что здесь, что там. Это моё условие. =)

В общем пузырь служит для закачки балласта. У земли дирижабль будут держать не мешки с песком или кирпичами, а воздух. Да, именно обычный воздух. Его полно вокруг, его можно насосом как закачивать так и откачивать и делать это быстро.

И первым делом мы посчитаем объем пузыря и остальные интересные параметры. Сейчас проспойлерю и покажу соотношение объемов уже просчитанное, а потом приступим к вычислениям.

Для проектирования пузыря запишем математическую модель задачи. Для этого нужно лишь вспомнить уравнение состояния идеального газа:

$pV=\frac m MRT$

здесь – давление, – объем, – масса, – молярная масса, $R=8.314 \: {Дж}/(мольK)$ – универсальная газовая постоянная, T – температура.

Для дальнейшей работы нам понадобятся молярные массы воздуха и водорода (он лучше чем гелий) (в системе СИ):

$M_{\mathit{возд}}=28.97 \cdot 10^{-3}\mathit{кг}/\mathit{моль}$ $M_{\mathit{вод}}=2\cdot10^{-3}\mathit{кг}/\mathit{моль}$

Оболочка с пузырем образуют систему (в произвольный момент времени), изображенную на рисунке 6.

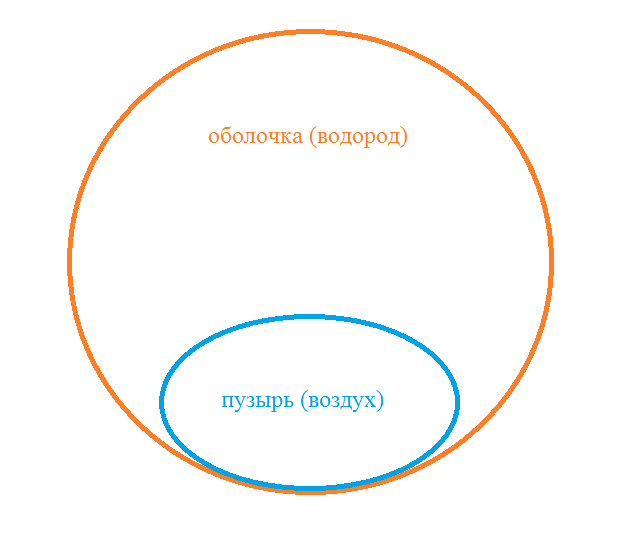
Объем дирижабля равен объему оболочки – величина постоянная, и в данном случае равна:

$V_Т=3.33 \: м^3$

здесь индекс Т означает «тела», то бишь объем всего тела (дирижабля).

А вот объем водорода, объем воздуха и масса воздуха – величины переменные, так как в процессе эксплуатации воздух то нагнетается, то откачивается из пузыря тем самым варьируя данные параметры.

Очевидно, что в оболочке и пузыре давления и температуры равны. Также понятно, что температура равна атмосферному, а давление равно атмосферному, но с некоторым избытком (который также является переменной величиной, ибо давление в оболочках не обязательно должно равняться строго атмосферному). Для каждого резервуара можно записать уравнение:

$k\left(h\right) \cdot P_{\mathit{атм}}\left(h\right) \cdot \left(V_Т-V_{\mathit{пуз}}\left(h\right)\right)=\frac{m_{\mathit{вод}}}{M_{\mathit{вод}}}R \cdot T\left(h\right)$ $k\left(h\right) \cdot P_{\mathit{атм}}\left(h\right) \cdot V_{\mathit{пуз}}\left(h\right)=\frac{m_{\mathit{возд}}\left(h\right)}{M_{\mathit{возд}}}R \cdot T\left(h\right)$

здесь переменные величины записаны как зависящие от высоты. В данных формулах фигурирует не само давление в оболочках, а коэффициент избыточного давления k, так удобнее (мне). Атмосферное давление и температура известные, они выше уже изображались графическими зависимостями. А вот остальные переменные пока неизвестные.

Поделим одно уравнение на другое:

$\frac{V_Т-V_{\mathit{пуз}}\left(h\right)}{V_{\mathit{пуз}}\left(h\right)}=\frac{m_{\mathit{вод}}}{M_{\mathit{вод}}} \cdot \frac{M_{\mathit{возд}}}{m_{\mathit{возд}}\left(h\right)}$

Немного преобразуем его арифметическими операциями:

$V_Т=\frac{m_{\mathit{вод}}}{M_{\mathit{вод}}} \cdot \frac{M_{\mathit{возд}}}{m_{\mathit{возд}}\left(h\right)} \cdot V_{\mathit{пуз}}\left(h\right)+V_{\mathit{пуз}}\left(h\right)$

Итого имеем:

$V_{\mathit{пуз}}\left(h\right)=\frac{V_Т}{1+\frac{m_{\mathit{вод}}}{M_{\mathit{вод}}} \cdot \frac{M_{\mathit{возд}}}{m_{\mathit{возд}}\left(h\right)}}$

Также мы можем записать еще одно уравнение – величина силы Архимеда равна силе тяжести (сократили на g):

$ρ_{\mathit{возд}}\left(h\right) \cdot V_Т=m_{\mathit{конст}}+m_{\mathit{вод}}+m_{\mathit{возд}}\left(h\right)$

Здесь плотность воздуха атмосферы зависит от высоты, а масса водорода и конструкции (под конструкцией имеется в виду и масса конструкции и полезный груз) – постоянные величины, но пока неизвестные.

Выразим из этого уравнение массу воздуха:

$m_{\mathit{возд}}\left(h\right)=ρ_{\mathit{возд}}\left(h\right) \cdot V_Т-m_{\mathit{конст}}-m_{\mathit{вод}}$

Подставляя эту зависимость в формулу для $V_{\mathit{пуз}}\left(h\right)$ будем практически иметь формулу, но в ней пока неизвестны два параметра - масса водорода и конструкции.

Найти их можно из следующих соображений. Нужно определиться на какую максимальную высоту будет летать дрон. Вот я уже определился, это 2000 м. Теперь запишем выше представленное уравнение в граничных точках:

$ρ_{\mathit{возд}}\left(0\right) \cdot V_Т=m_{\mathit{конст}}+m_{\mathit{вод}}+m_{\mathit{возд}}\left(0\right)$ $ρ_{\mathit{возд}}\left(2000\right) \cdot V_Т=m_{\mathit{конст}}+m_{\mathit{вод}}+m_{\mathit{возд}}\left(2000\right)$

Но так как масса воздуха в пузыре на максимальной высоте будет равна нулю (он то нам нужен как хранитель балласта, а на максимальной высоте по логике вещей весь балласт должен быть сброшен), имеем:

Вычитая из первого уравнения второе, определим массу воздуха на нулевой высоте:

$m_{\mathit{возд}}\left(0\right)=\left(ρ_{\mathit{возд}}\left(0\right)-ρ_{\mathit{возд}}\left(2000\right)\right) \cdot V_Т$

Теперь запишем уравнение состояния газа для пузыря на нулевой высоте:

$V_{\mathit{пуз}}\left(0\right)=m_{\mathit{возд}}\left(0\right)\frac{R \cdot T\left(0\right)}{M_{\mathit{возд}} \cdot k\left(0\right) \cdot P_{\mathit{атм}}\left(0\right)}$

Здесь справа всё известно, окроме коэффициента k на нулевой высоте. Из опыта могу открыть секрет, для оболочек изготовленных из металлизированных пленок его лучше задать равным у земли примерно 1.03. При 1.05 оболочка лопнет... А при 1.03 она уже достаточно хорошо держит форму, да что там хорошо - она натянута как барабан. Избыточное давление при этом как нетрудно понять примерно 3 кПа.

Итого у нас уже имеется и объем пузыря (ведь на нулевой высоте он будет максимальным, загружен балластом до краев).

А вот теперь пришло время записать уравнение сост. ид. газа для оболочки дирижабля на нулевой высоте и найти таким образом массу водорода:

$m_{\mathit{вод}}=\frac{k\left(0\right) \cdot P_{\mathit{атм}}\left(0\right) \cdot M_{\mathit{вод}}}{R \cdot T\left(0\right)} \cdot \left(V_Т-V_{\mathit{пуз}}\left(0\right)\right)$

И массу конструкции теперь легко определить:

$m_{\mathit{конст}}=ρ_{\mathit{возд}}\left(2000\right) \cdot V_Т-m_{\mathit{вод}}$

Вроде все как-то запутанно, но на самом деле тут обычная система линейных уравнений 4-го порядка, можно и так: сначала записать и решить как слау.

Итого, значения получаются равными для нашего случая:

$m_{\mathit{вод}}=0.23985 \: \mathit{кг}$ , $m_{\mathit{конст}}=3.112 \: \mathit{кг}$ , $m_{\mathit{возд}}\left(0\right)=0.7276 \: \mathit{кг}$ , $V_{\mathit{пуз}}\left(0\right)=0.57664 \: м^3$ .

Теперь, когда всё известно, можно и графики зависимостей построить по формулам:

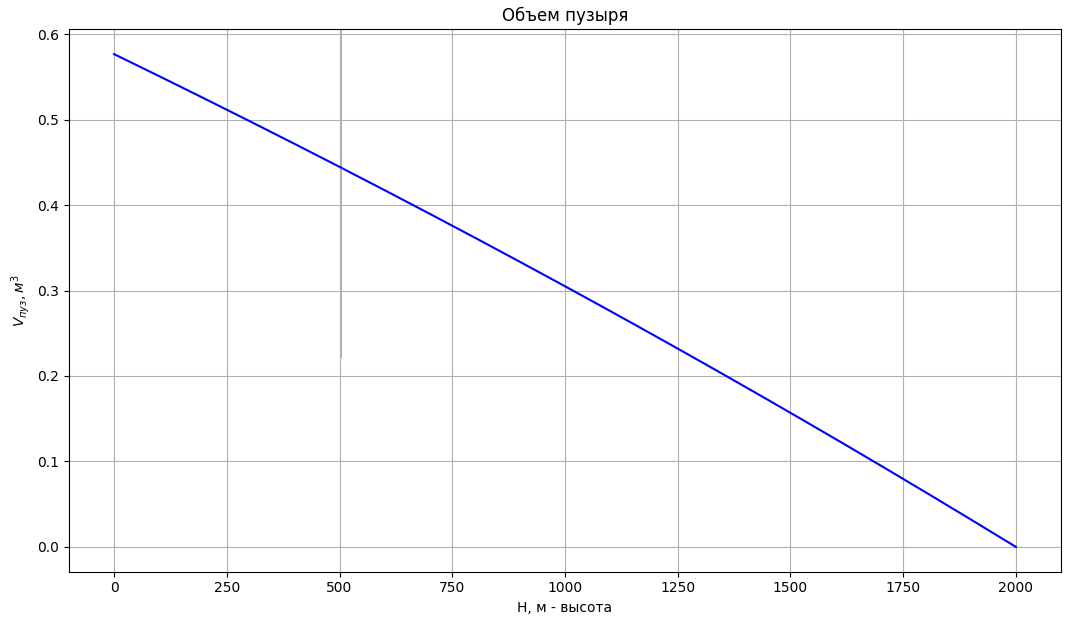
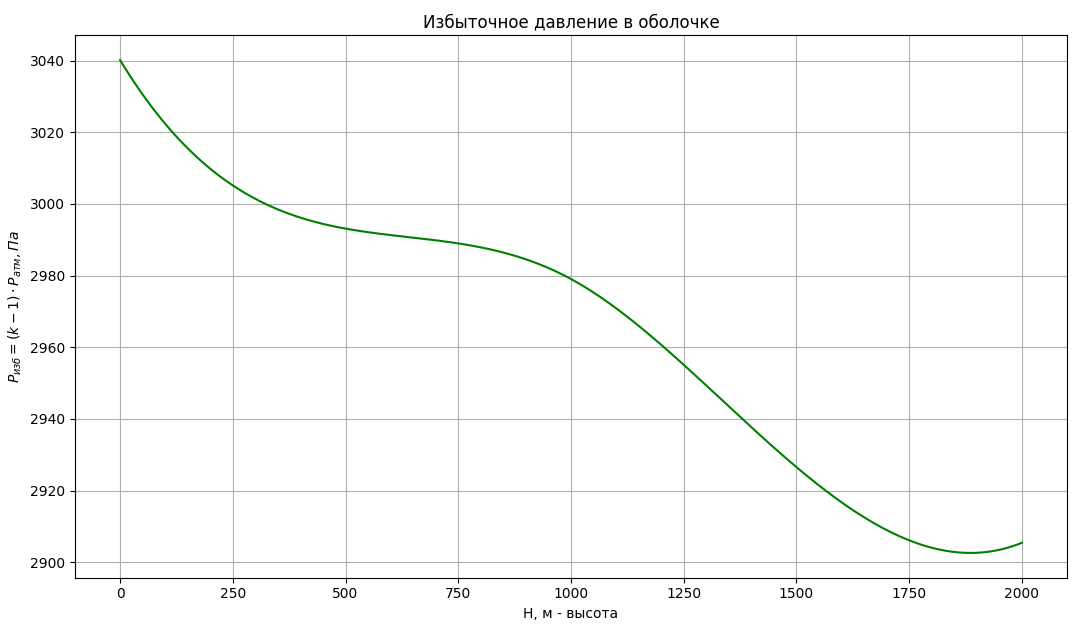
$V_{\mathit{пуз}}\left(h\right)=\frac{V_Т}{1+\frac{m_{\mathit{вод}}}{M_{\mathit{вод}}} \cdot \frac{M_{\mathit{возд}}}{ρ_{\mathit{возд}}\left(h\right) \cdot V_Т-m_{\mathit{конст}}-m_{\mathit{вод}}}}$ $k\left(h\right)=\frac{m_{\mathit{вод}}}{M_{\mathit{вод}}}R \cdot \frac{T\left(h\right)}{P_{\mathit{атм}}\left(h\right) \cdot \left(V_Т-V_{\mathit{пуз}}\left(h\right)\right)}$

Ну вот и всё. Всё устраивает, всё правильно получается. Можно сказать пузырь готов. Рассчитать его размеры исходя из объема можно.

Таким образом дрон-дирижабль оснащенный пузырем внутри способен взлетать на высоту 2 км и при этом не то что не лопнет, так он еще и форму держать будет и давление практически постоянное, и колебания атмосферы можно держать в узде. Всё.

А потом можно доделать дрон до конца и летать в реальности примерно как в симуляции:

Спасибо за внимание.

Источник: https://habr.com/ru/post/577930/

Вернуться к списку

Интересные статьи

Узкоспециализированная видеореклама на YouTube: как и с чего начать

В наше время медийная реклама — один из самых эффективных способов донести до целевой аудитории информацию о своем продукте и завоевать ее доверие. Но когда дело касается узкоспециализиро...

Описание сервиса маркетплейс 1С-Битрикс. Как начать разрабатывать приложения для marketplace?

Маркетплейс – это сервис от 1С-Битрикс, который позволяет разработчикам делиться своими решениями с широкой аудиторией, состоящей из клиентов и других разработчиков.

Netflix за 45 минут: Краткий рассказ о system design-интервью, чего ожидать + подборка полезных ссылок

В нашем блоге мы много пишем о построении карьеры в ИТ в разных странах, поиске работы, отличиях в процессе собеседований крупных компаний. В сегодняшней статье мы пойдем дальше и...

PocketBook: итоги года, или Чего нового и важного случилось в 2019 году

Приветствую всех! 2019-й вот-вот завершится, и поэтому сегодня уже вполне уместно поговорить об итогах года. Точнее, не столько об итогах, сколько о самых важных событиях для компании PocketBook ...

Southbridge в Челябинске и Битрикс в Kubernetes

В Челябинске проходят митапы системных администраторов Sysadminka, и на последнем из них я делал доклад о нашем решении для работы приложений на 1С-Битрикс в Kubernetes. Битрикс, Kubernetes, Сep...