Шифрование на основе квантовых блужданий для Интернета Вещей в сетях 5G

В наше время каждый слышал о сотовых сетях нового поколения 5G. Неотъемлемой частью 5G является поддержка сценариев Интернета Вещей. А что вообще такое Интернет Вещей? Если говорить простыми словами, то это набор устройств, которые должны взаимодействовать друг с другом при минимальном вмешательстве человека. Исследователи считают, что сети 5G могут быть использованы для большого количества различных сценариев Интернета Вещей, таких как медицина, умные города, регулирование транспортных заторов, обеспечение работы аварийных служб, обеспечение работы промышленных предприятий и т.д. Для реализации таких сценариев сети 5G предусматривают новые сетевые архитектуры, сервисы, приложения и прочие механизмы.

При этом важнейшей задачей при проектировании таких сетей является обеспечение безопасности при передаче и хранении данных. Особенно важное внимание нужно обратить на проблему безопасности мультимедийного контента, который предполагается для передачи в большом количестве сценариев. Современные классические (не квантовые) методы криптографии всё ещё являются достаточно надежными для использования в современных технологиях. Однако, стремительное развитие квантовых вычислений ставит под сомнение надежность классических методов, основанных на математических вычислениях, в недалеком будущем. Поэтому уже сейчас необходимо создавать и развивать квантовые методы шифрования для будущих приложений. В данной статье мы рассмотрим шифрование на основе квантовых блужданий для видео-трафика и файлов, предлагаемые для использований в сценариях Интернета Вещей в сетях 5G.

Квантовые блуждания

Думаю, что многие слышали про случайные блуждания из математики, физики или другой дисциплины. Не вдаваясь в строгие математические термины скажем, что случайное блуждание это процесс, в котором некий объект периодически совершает шаги в произвольном направлении. Типичным примером подобного процесса является задача про пьяного матроса, который каждую условную секунду совершает шаг влево или вправо с одинаковой вероятностью. Интересной особенностью тут является то, что в среднем «ходок» удаляется от стартового положения на некоторое расстояние, причем это расстояние растет как квадратный корень из числа шагов. Данная модель имеет огромное количество приложений в различных дисциплинах, например она используется для моделирования диффузии.

По аналогии с классическими случайными блужданиями существуют квантовые блуждания. Если вы имеете какое-то представление о квантовой механике, то знаете, что здесь не имеет смысла говорить о каких-либо положениях частицы, а можно говорить только о вероятностях оказаться в тех или иных положениях. Мы будем рассматривать блуждание частицы в кольце, состоящем из N вершин. Состояние частицы при этом состоит из двух частей: «монетка» (это может быть спин электрона) и «ходок» (отвечает за положение в кольце). При этом шаг заключается в применении операторов «подбрасывания монеты» и сдвига. Сложные формулы из квантовой механики можно посмотреть в спойлере, здесь заметим лишь, что в результате после произвольного числа шагов вычисляются вероятности нахождения в каждом из положений кольца. Эти вероятности и являются интересующим нас результатом квантовых блужданий.

Формулы из квантовой механики

Функция состояния состоит из «монетки» |c⟩ и «ходокa» |x⟩:

Опрератор шага блуждания состоит из двух частей:

$\hat{E} = \hat{F}(\hat{I} \otimes \hat{O}),$

параметрического опрератора «подбрасывания монеты»:

$\hat{O} = \begin{pmatrix} \cos \alpha & \sin \alpha \\ \sin \alpha & -\cos \alpha \end{pmatrix}$

и оператора «сдвига»:

$\hat{F} = \sum_{x =0}^{N-1} |(x + 1)~mod~N, 0 \rangle \langle x, 0| + \sum_{x =0}^{N-1} |(x - 1)~mod~N, 1 \rangle \langle x, 1|.$

Фунция состояния после w шагов:

$|Q \rangle_{w} = (\hat{E})^{w} |Q \rangle_{initial}.$

При этом получается следующее распределение вероятностей:

$P(x, w) = \sum_{c \in \{0, 1\}}\left| \langle x, c| (\hat{E})^{w}| Q_{initial} \rangle \right|^2$

Формулы для двумерного случая аналогичны, при этом там используется два оператора подбрасывания монеты с разными параметрами и два оператора шага блуждания. Последовательность применения этих операторов определяется заданной битовой строкой S. Подробнее можно почитать здесь.

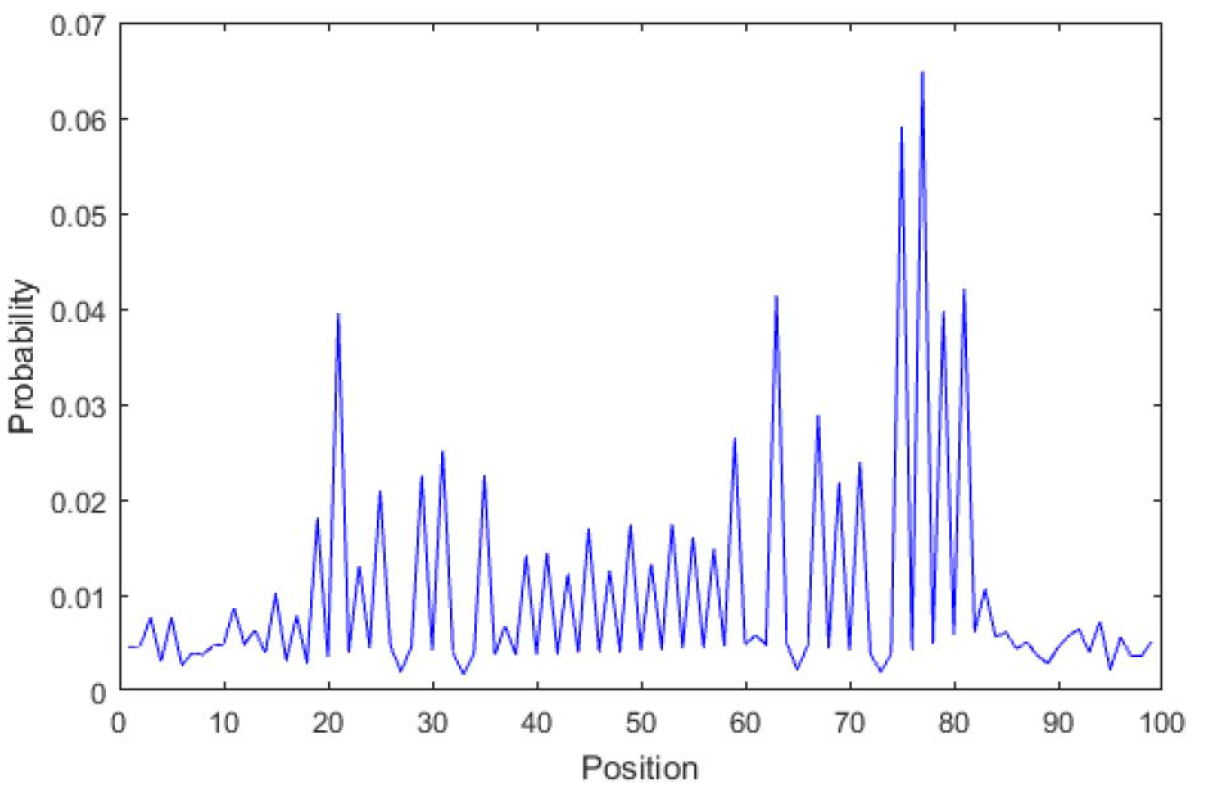
Для предложенных ниже алгоритмов используется два вида блужданий: одномерные и двумерные. Примеры распределений вероятности в этих случаях можно видеть на рисунках ниже. Квантовые блуждания могу быть реализованы на квантовых компьютерах, как например здесь.

S-блок

Фундаментальным элементом блочных шифров является -блок или блок подстановок. Этот блок осуществляет нелинейное преобразование одной группы битов в другую. Рассмотрим реализацию такого блока на основе одномерного квантового блуждания.

Конструирование S-блока, состоящего из B элементов включает следующие шаги:

Выбираем секретный ключ, то есть параметры одномерного квантового блуждания: размер кольца N, количество шагов, начальное состояние «монеты» и параметр оператора «подбрасывания монеты». В результате блуждания получаем вектор вероятностей размера N.
Изменяем размер вектора в соответствии с длиной B S-блока, получаем вектор R.
Упорядочиваем элементы вектора R по возрастанию, получаем вектор S.
В качестве последовательности для S-блока выбираем последовательность индексов элементов вектора R в векторе S.

Пример такого конструирования представлен на схеме:

Конструирование S-блока на основе квантового блуждания

Шифрование видео

Как уже было отмечено выше, шифрование видео трафика является важной задачей в применении к Интернету Вещей в сетях 5G. Рассмотрим алгоритм шифрования видео, состоящего из f кадров размера m x n и 3 каналов:

Выбираем секретный ключ, то есть параметры двумерного квантового блуждания: размер кольца N, битовая строка, описывающая шаги блуждания, начальное состояние “монетки” и параметры двух операторов “подбрасывания монетки”. В результате блуждания получаем матрицу вероятностей размера N × N.
Изменяем размер матрицы в соответствии с размером последовательности кадров.
Переводим получившуюся матрицу в матрицу K целых чисел в диапазоне от 0 до 255.
Выполняем побитовую операцию xor (исключающее или) между кадрами и матрицей K.
Конструируем два S-блока размерами n и m соответственно по алгоритму из предыдущего пункта.
Применяем S-блоки для перестановки битов в каждом кадре и получаем закодированные кадры

Тоже самое формулами

$\begin{align} & 1) (N, S, \chi, \delta, \alpha_0, \alpha_1) \rightarrow P(N \times N) \\ & 2) R = resize(P, f \times m \times n \times 3) \\ & 3) K_i = fix(R_i \cdot 10^8) mod 256 \\ & 4) X_i = bitxor(farme_i, K_i) \\ & 5) (N, w, \chi, \delta, \alpha) \rightarrow S_n, S_m \\ & 6) EncFrame_i = permutation(X_i, S_n, S_m) \end{align}$

Дешифрование видео происходит путем выполнения данных действий в обратном порядке. Схема шифрования и расшифрования представлена на рисунке ниже.

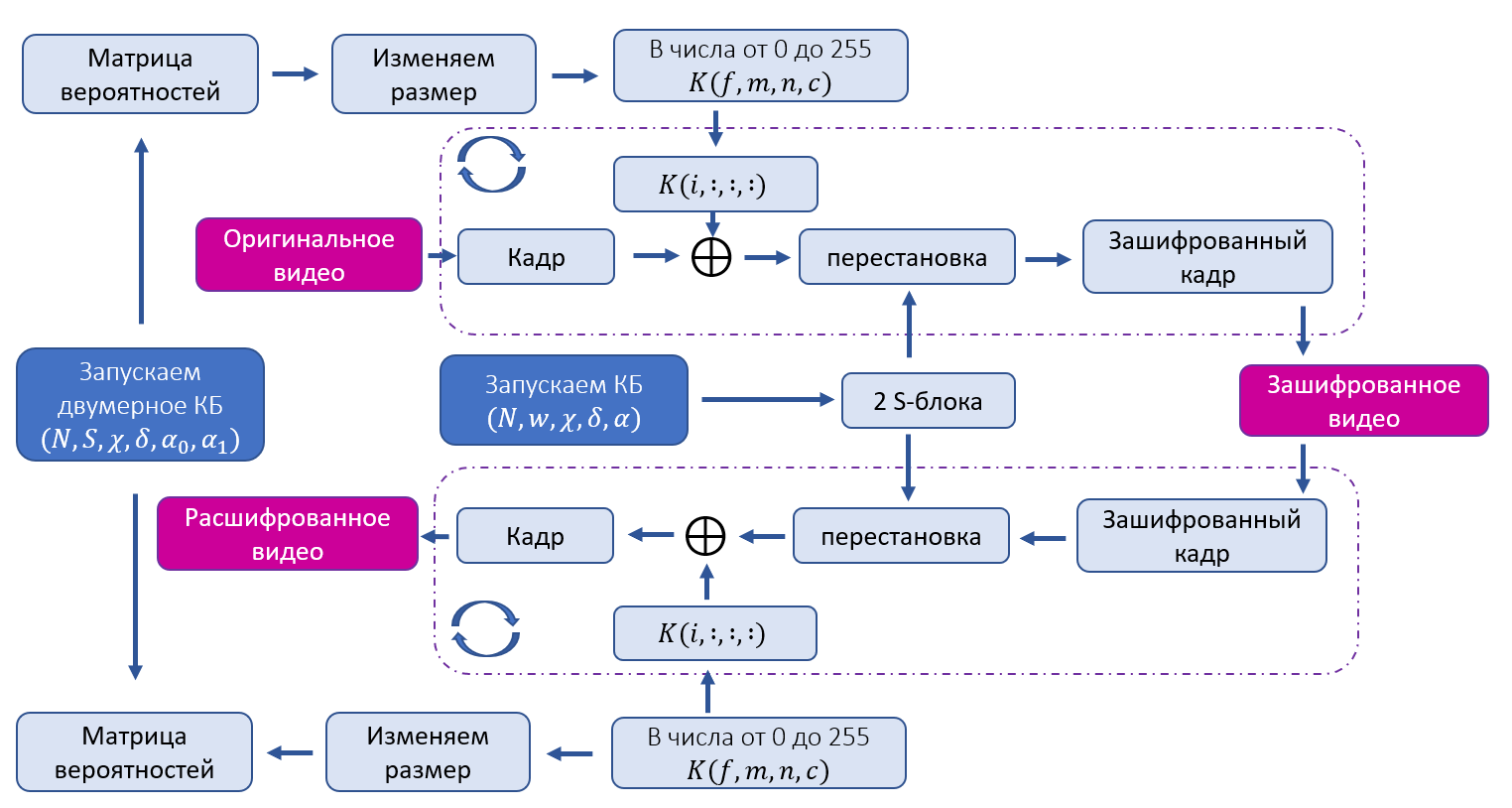
Далее на рисунке приведен пример шифрования и расшифрования кадра. Ниже располагаются графики корреляции в соседних пикселях красного канала по разным направлениям для оригинального (сверху) и зашифрованного (снизу) кадров. Как видно, после шифрования пиксели перестали коррелировать, а значит потенциальный злоумышленник не сможет извлечь информацию из зашифрованных кадров.

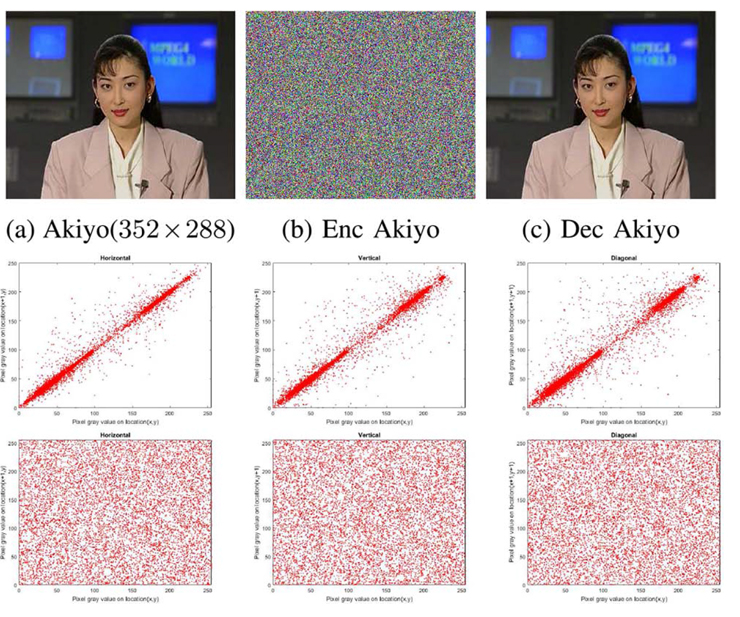
Шифрование файлов

В данном разделе рассмотрим алгоритм шифрования файлов для хранения в облачном хранилище сетей 5G. Это могут быть файлы любого типа: изображение, аудио, видео, текст и т.д., так как алгоритм работает с ними как с битовыми наборами. Для шифрования битового набора BF выполняются следующие действия:

Вычисляем матрицу вероятностей P размера N × N (аналогично пункту 1 алгоритма шифрования видео).
Переводим матрицу P в вектор PK размера length(BF) / 8.
Переводим вектор PK в битовый вектор K.
Выполняем операцию побитовое xor (исключающее или) между BF и K.
Конструируем S-блок размером 256 алгоритму из соответствующего пункта
Применяем S-блок к каждому элементу полученной последовательности и получаем закодированный файл.

Тоже самое формулами

$\begin{align} & 1) (N, S, \chi, \delta, \alpha_0, \alpha_1) \rightarrow P(N \times N) \\ & 2) R = resize(P, length(BF) / 8) \\ & 3) K = dec2bin(fix(PK \cdot 10^8)~ mod ~2^8, 8) \\ & 4) X = bitxor(BF, K) \\ & 5) (N, w, \chi, \delta, \alpha) \rightarrow S_{256} \\ & 6) EncFile = permutation(X, S_{256}) \end{align}$

Расшифрование происходит путем выполнения данных действий в обратном порядке. Схема шифрования и расшифрования представлена ниже.

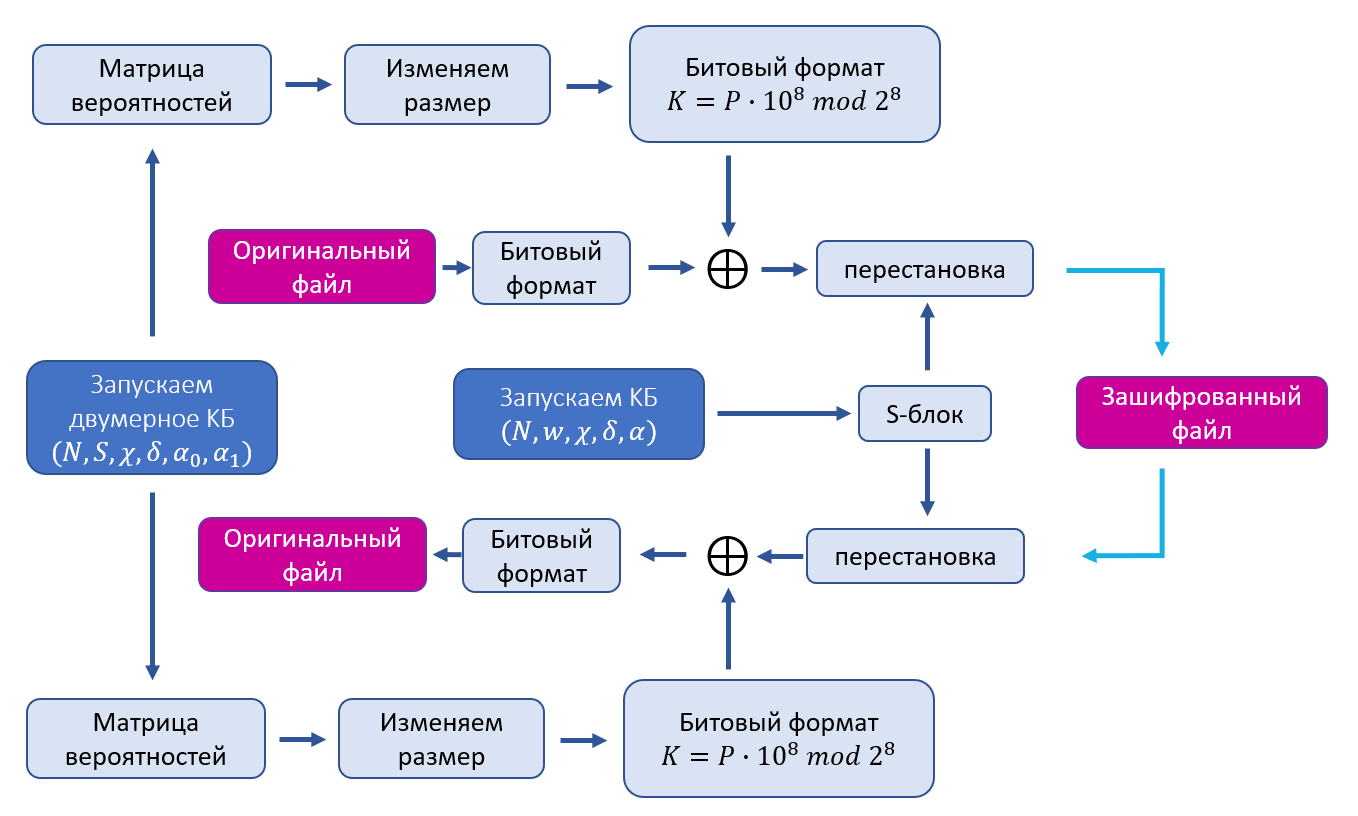
Основным преимуществом данных алгоритмов по сравнению с классическими является то, что генерация ключевого потока в них основана не на математических вычислениях, а на физических свойствах квантовых систем. Выше было показана эффективность алгоритма с точки зрения коэффициента корреляции между соседними пикселями. Алгоритмы являются эффективными и с точки зрения других криптографических метрик, подробнее об этом можно почитать здесь.

Сценарий использования в сетях 5G

Наконец, попробуем представить как будет выглядеть сеть 5G, в которой будут использоваться предложенные алгоритмы. Различные приложения обмениваются информацией через базовые станции 5G, которые в том числе взаимодействуют с облачными хранилищами. Пользователи используют параметры ключей для шифрования данных по рассмотренным выше алгоритмам. Зашифрованные данные передаются через сеть другим пользователям или в облачное хранилище. При этом пользователи обмениваются параметрами ключей через защищенные квантовые каналы или иным защищенным методом. При несанкционированном запросе на чтение данных из облачного хранилища удастся получить лишь зашифрованные данные, не несущие никакой информации.

Сценарий использования алгоритмов в сетях 5G

В заключение стоит отметить, что несмотря на то, что в оригинальной работе данные алгоритмы предлагаются к использованию в сетях 5G, ничто не запрещает использовать их в любух других сетях и системах. Так что не удивляйтесь, если уже в ближайшем будущем подобные алгоритмы станут частью нашей обыденной жизни.

Источник: https://habr.com/ru/post/531774/

Вернуться к списку

Интересные статьи

Программирование устройств на основе модуля ESP32

Микроконтроллер — это интегральная схема, способная выполнять программы. Сегодня на рынке представлено множество таких моделей от самых разных производителей. Цены на эти устройства п...

Кейс: Автоматизация инстамагазина. Продаёте через сообщения в соцсетях?

Сегодня решил-таки описать последний проект, т.к. это прикольное и в то же время не стандартное решение. Начало Есть большой сегмент магазинов, услуг и вообще бизнес моделей, по которой в...

Настройка в интернет-магазине на 1С-Битрикс бизнес-смыслов

Бизнес-смыслы появились в Битриксе в начале 2016 года, но мало кто понимает, как их правильно использовать для удобной настройки интернет-магазинов.

5 вещей, которые чаще всего не понимают новички в JavaScript

Всем привет! В конце сентября в OTUS стартует новый поток курса «Fullstack разработчик JavaScript». В преддверии начала занятий хотим поделиться с вами авторской статьей, подготовленной специальн...

Как id Software создавала Wolfenstein 3D на основе технологий из Commander Keen

Данная статья является фрагментом книги Game Engine Black Book: Wolfenstein 3D — подробного исследования, посвящённого истории, коду и разработке оказавшего огромное влияние на игровую отрасль ...