Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В этом посте описывается генератор уровней для моей игры-головоломки Linjat. Пост можно читать и без подготовки, но он легче усвоится, если сыграть в несколько уровней. Исходный код я выложил на github; всё обсуждаемое в статье находится в файле
Примерный план поста:
Чтобы понять, как работает генератор уровней, нужно, к сожалению, разобраться с правилами игры. К счастью, они очень просты. Головоломка состоит из сетки, содержащей пустые квадраты, числа и точки. Пример:

Цель игрока — прочертить вертикальную или горизонтальную линию через каждое из чисел при соблюдении трёх условий:
Пример решения:
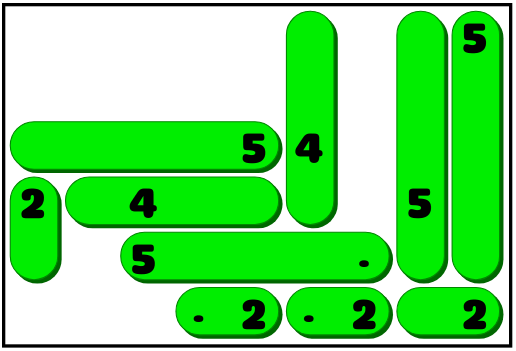
Ура! Дизайн игры готов, UI реализован, и теперь единственное, что осталось — найти несколько сотен хороших головоломок. А для подобных игр обычно не имеет смысла пытаться создавать такие головоломки вручную. Это работа для компьютера.
Что делает головоломку для этой игры хорошей? Я склонен считать, что игры-головоломки можно разбить на две категории. Есть игры, в которых ты исследуешь сложное пространство состояний от начала до конца (например, Sokoban или Rush Hour), и в которых может быть и не очевидно, какие состояния существуют в игре. И есть игры, в которых все состояния известны с самого начала, и мы постепенно вылепливаем пространство состояний с помощью процесса устранения лишних (например, Sudoku или Picross). Моя игра определённо относится ко второй категории.
Игроки предъявляют очень отличающиеся требования к этим разным видам головоломок. Во втором случае они ожидают, что головоломку можно решить только дедукцией, и что им никогда не понадобится возврат назад/угадывание/процесс проб и ошибок[0][1].
Недостаточно знать, можно ли решить головоломку только с помощью логики. Кроме того, нам нужно как-то понять, насколько хороши создаваемые головоломки. В противном случае большинство уровней будет просто тривиальным шлаком. В идеальной ситуации этот принцип можно было использовать также для создания плавной кривой прогресса, чтобы при прохождении игроком игры уровни постепенно становились сложнее.
Первый шаг к удовлетворению этих требований — создание солвера игры, оптимизированного для этой цели. Солвер грубого перебора с возвратом назад (backtracking) позволит быстро и точно определить, решаема ли головоломка; кроме того, его можно модифицировать, чтобы он определял, является ли решение уникальным. Но он не может дать представления о том, насколько сложна на самом деле головоломка, потому что люди решают их по-другому. Солвер должен имитировать поведение человека.
Как же человек решает эту головоломку? Вот пара очевидных ходов, которым учит внутриигровой туториал:
Подобные рассуждения — самая основа игры. Игрок ищет способы растянуть немного одну линию, а затем снова изучает поле, потому что оно может дать ему информацию, чтобы сделать ещё один логический вывод. Создания солвера, следующего этим правилам, будет достаточно, чтобы определить, сможет ли человек решить головоломку без возврата назад.
Однако это ничего не говорит нам о сложности или интересности уровня. Кроме решаемости, нам каким-то образом нужно численно оценить сложность.
Очевидная первая идея для функции оценки: чем больше ходов требуется для решения головоломки, тем она сложнее. Вероятно, в других играх это хорошая метрика, но моей, скорее всего, важнее количество допустимых ходов, которые есть у игрока. Если игрок может сделать 10 логических выводов, то он, скорее всего, найдёт один из них очень быстро. Если верный ход только один, то это потребует больше времени.
То есть в качестве первой аппроксимации нам нужно, чтобы дерево решений было глубоким и узким: есть длинная зависимость ходов от начала до конца, и в каждый момент времени есть только малое количество способов продвинуться вверх по цепочке[2].
Как нам определить ширину и глубину дерева? Однократное решение головоломки и оценка созданного дерева не дадут точного ответа. Точный порядок делаемых ходов влияет на форму дерева. Нам нужно рассмотреть все возможные решения и сделать с ними что-то вроде оптимизации по лучшим и худшим случаям. Мне знакома техника грубого перебора графов поиска в играх-головоломках, но для этого проекта я хотел создать однопроходной солвер, а не какой-то исчерпывающий поиск. Из-за фазы оптимизации я стремился к тому, чтобы время выполнения солвера измерялось не в секундах, а в миллисекундах.
Я решил этого не делать. Вместо этого мой солвер на самом деле не делает один ход за раз, а решает головоломку по слоям: взяв состояние, он находит все допустимые ходы, которые можно сделать. Затем применяет все эти ходы одновременно и начинает заново в новом состоянии. Количество слоёв и максимальное число ходов, найденное на одном слое, затем используются как приближенные значения глубины и ширины дерева поиска в целом.
Вот как при этой модели выглядит решение одной из сложных головоломок. Пунктирные линии — это линии, растянутые на этом слое солвера, сплошные — те, которые не менялись. Зелёные линии имеют правильную длину, красные ещё не завершены.

Следующая проблема заключается в том, что все делаемые игроком ходы создаются равными. То, что мы перечислили в начале этого раздела — просто здравый смысл. Вот пример более сложного правила дедукции, на поиск которого потребуется немного больше размышлений. Рассмотрим такое поле:

Точки в C и D можно покрыть только пятёркой и средней четвёркой (и ни одно число не может покрыть обе точки одновременно). Это значит, что четвёрка посередине должна покрыть одну точку из двух, а значит не может быть использовала для покрытия A. Следовательно, точку A должна закрыть четвёрка в левом нижнем углу.
Очевидно, что было бы глупо считать эту цепочку рассуждений равной простому выводу «этой точки можно достичь только из этого числа». Можно ли в функции оценки придавать этим более сложным правилам больший вес? К сожалению, в солвере на основе слоёв это невозможно, потому что в нём не гарантировано нахождение решения с наименьшими затратами. Это не только теоретическая проблема — на практике довольно часто бывает так, что часть поля решаема или единственным сложным рассуждением, или цепочкой гораздо более простых ходов. По сути, солвер на основе слоёв находит кратчайший, а не самый малозатратный путь, и это нельзя отразить в функции оценки.
В результате я пришёл к такому решению: я изменил солвер таким образом, чтобы каждый слой состоял только из одного типа рассуждений. Алгоритм обходит правила рассуждений в приблизительном порядке сложности. Если правило находит какие-то ходы, то они применяются, и на этом итерация завершается, а следующая итерация начинает список с самого начала.
Затем решению присваивается оценка: каждому слою назначаются затраты на основании одного правила, которое в нём использовалось. Это всё равно не гарантирует, что решение будет самым малозатратным, но при правильном подборе весов алгоритм хотя бы не будет находить затратное решение, если существует дешёвое.
Кроме того, это очень походит на то, как головоломки решают люди. Они сначала пытаются найти лёгкие решения, и начинают активно шевелить мозгами, только если простых ходов нет.
Предыдущий раздел определял, хорош или плох конкретный уровень. Но только этого недостаточно, нам нужно ещё как-то сгенерировать уровни, чтобы солвер мог их оценить. Очень маловероятно, что случайно сгенерированный мир будет решаемым, не говоря уже об интересности.
Основная идея (она ни в коем случае не нова) заключается в попеременном использовании солвера и генератора. Давайте начнём с головоломки, которая, вероятно, нерешаема: просто расположим в случайных квадратах ячейки числа от двух до пяти:

Солвер работает до тех пор, пока не сможет дальше развиваться:
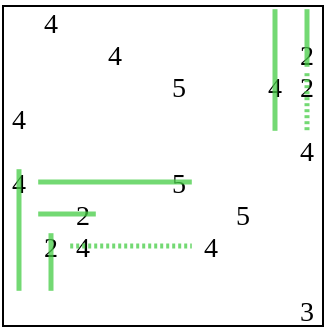
Затем генератор добавляет в головоломку ещё информации в виде точки, после чего продолжается выполнение солвера.
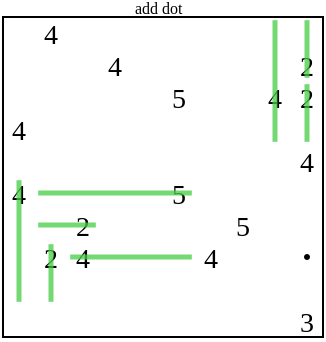
В этом случае добавленной точки солверу недостаточно для дальнейшего развития. Потом генератор будет продолжать добавлять новые точки, пока это не удовлетворит солвер:

А затем солвер продолжает свою обычную работу:

Этот процесс продолжается или пока головоломка не будет решена, или пока не останется больше информации для добавления (например, когда каждая клетка, которую можно достичь из числа, уже содержит точку).
Этот метод работает только в том случае, если добавляемая новая информация не может сделать неверными любые из ранее сделанных выводов. Это было бы сложно сделать при добавлении в сетку чисел[3]. Но добавление на поле новых точек обладает таким свойством; по крайней мере, для правил рассуждения, которые я использую в этой программе.
Куда алгоритм должен добавлять точки? В конце концов я решил добавлять их в пустое пространство, которое можно закрыть в начальном состоянии наибольшим количеством линий, чтобы каждая точка стремилась выдавать как можно меньше информации. Я не пытался специально разместить точку в том месте, где она была бы полезна для продвижения в решении головоломки на момент, когда солвер застрянет. Это создаёт очень удобный эффект: большинство точек кажется в начале головоломки совершенно бесполезными, из-за чего головоломка кажется сложнее, чем есть на самом деле. Если всё это множество очевидных ходов, которые может сделать игрок, но почему-то не один из них не срабатывает в должной мере. В результате получилось, что генератор головоломок ведёт себя немного по-свински.
Этот процесс не всегда создаёт решение, но он довольно быстр (порядка 50-100 миллисекунд), поэтому для генерации уровня можно просто повторить его несколько раз. К сожалению, обычно он создаёт посредственные головоломки. С самого начала есть слишком много очевидных ходов, поле заполняется очень быстро и дерево решений оказывается довольно неглубоким.
Описанный выше процесс создавал посредственные головоломки. На последнем этапе я использую эти уровни как основу для процесса оптимизации. Он работает следующим образом.
Оптимизатор создаёт пул, в котором содержится до 10 вариантов головоломки. Пул инициализируется новой сгенерированной случайной головоломкой. На каждой итерации оптимизатор выбирает из пула одну головоломку и выполняет её мутацию.
Мутация удаляет все точки, а затем немного изменяет числа (т.е. уменьшает/увеличивает значение случайно выбранного числа или перемещает число в другую клетку сетки). Можно применить к полю одновременно несколько мутаций. Затем мы запускаем солвер в специальном режиме генерации уровней, описанном в предыдущем разделе. Он добавляет в головоломку достаточное количество точек, чтобы она снова стала решаемой.
После этого мы снова запускаем солвер, на этот раз в обычном режиме. Во время этого прогона солвер отслеживает a) глубину дерева решений, b) частоту необходимости разных видов правил, c) ширину дерева решений в разные моменты времени. Головоломка оценивается на основании описанных выше критериев. Функция оценки предпочитает глубокие и узкие решения, а уровни повышенной сложности также придают больший вес головоломкам, в которых требуется использовать более сложные правила рассуждений.
Затем в пул добавляется новая головоломка. Если в пуле содержится больше 10 головоломок, то наихудшая отбрасывается.
Этот процесс повторяется несколько раз (меня устроило примерно 10000-50000 итераций). После этого версия головоломки с наибольшей оценкой сохраняется в базу данных уровней головоломки. Вот как выглядит прогресс наилучшей головоломки на протяжении одного прогона оптимизации:

Я пробовал использовать и другие способы структурирования оптимизации. В одной версии использовалась имитация отжига, другие были генетическими алгоритмами с различными операциями кроссинговера. Ни одно из решений не проявило себя так же хорошо, как наивный алгоритм с пулом восходящих к вершине вариантов.
Когда головоломка имеет уникальное единственное решение, то возникает интересное затруднение. Можно ли допускать, чтобы игрок предполагал, что решение одно, и делал выводы исходя из этого? Будет ли честно, если генератор головоломок предположит, что игрок так и сделает?
В посте на HackerNews я говорил, что существует четыре варианта подхода к такой ситуации:
Изначально я выбрал последний вариант, и это было ужасной ошибкой. Оказалось, что я учёл только один способ, которым уникальность решения приводила к утечке информации, и он на самом деле довольно редок. Но есть и другие; один из них по сути присутствовал в каждом генерируемом мной уровне и часто приводил к тому, что решение становилось тривиальным. Поэтому в мае 2019 года я изменил режимы Hard и Expert, использовав третий вариант.
Самый раздражающий случай — это двойка с пунктирной линией на таком поле:
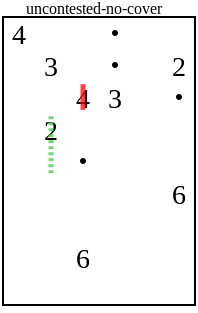
Почему хитрый игрок может сделать такой вывод? Двойка может закрывать любой из четырёх соседних квадратов. Ни в одном из них нет точек, поэтому они необязательно должны быть закрыты линией. А находящийся внизу квадрат не имеет наложений ни с какими другими числами. Если существует единственное решение, то это должен быть случай, когда другие числа закрывают остальные три квадрата, а двойка закрывает квадрат под ней.
Решение заключается в том, чтобы при распознавании таких случаев добавлять ещё несколько точек:

Ещё один распространённый случай — двойка с пунктиром на этом поле:
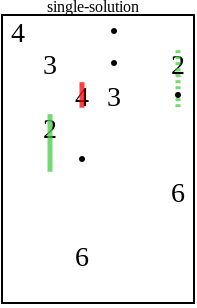
Квадраты слева и сверху от двойки ничем не отличаются. Ни в одном из них нет точки, и ни один нельзя достичь из любого другого числа. Любое решение, в котором двойка закрывает верхний квадрат, будет иметь соответствующее решение, в котором она закрывает левый квадрат, и наоборот. Если бы существовало единственное уникальное решение, то этого не могло бы быть, и двойка должна была закрывать нижний квадрат.
Подобный тип случаев я решил способом «если болит, то не трогай». Солвер применял это правило на раннем этапе в списке приоритетов и присваивал таким ходам большой отрицательный вес. Головоломки с такой особенностью обычно отбрасываются оптимизатором, а немногие оставшиеся отбрасываются на этапе окончательного выбора уровней для опубликованной игры.
Это не полный список, во время плейтестинга с намеренным поиском ошибок я нашёл множество других правил для уникальных решений. Но большинство из них казались редкими и их было довольно обнаружить, поэтому они не очень упрощали игру. Если кто-то решит головоломку, пользуясь подобными рассуждениями, то я не буду ставить это им в вину.
Изначально игра разрабатывалась как эксперимент по процедурной генерации головоломок. Дизайн игры и генератор шли рука об руку, поэтому сами техники сложно применить напрямую в других играх.
Вопрос, на который у меня нет ответа: оправдало ли себя вложение таких усилий в процедурную генерацию? Отзывы игроков о дизайне уровней были очень противоречивыми. В положительных комментариях обычно говорилось о том, что в головоломках всегда ощущается какая-то хитрая уловка. В большинстве негативных отзывов мне писали, что в игре не достаёт градиента сложности.
У меня есть ещё пара головоломок в зачаточной стадии, и мне так понравился генератор, что скорее всего для них я использую подобный процедурный подход. Изменю я только одно: с самого начала буду проводить активный плейтестинг с поиском ошибок.
[0] Или, по крайней мере, так мне казалось. Но когда я понаблюдал за игроками вживую, то почти половина из них просто делала догадки, а затем итеративно их прорабатывала. Ну да ладно.
[1] Читателям моей статьи также стоит прочитать статью Solving Minesweeper and making it better Магнуса Хоффа.
[2] Уточню, что глубина/узость дерева — это метрика, которую я посчитал значимой для своей игры, а не для всех других головоломок. Например, существует хороший аргумент о том, что головоломка Rush Hour интересна, если в ней есть несколько путей к решению почти, но не совсем одинаковой длины. Но так получилось потому, что Rush Hour — это игра на поиск кратчайшего решения, а не просто какого-нибудь решения.
[3] За исключением добавления единиц. В первой версии головоломки не было точек, и план заключался в том, чтобы при необходимости дополнительной информации генератор добавлял единицы. Но это казалось слишком ограничивающим.
src/main.cc.Примерный план поста:
- Linjat — это логическая игра, в которой нужно закрыть все числа и точки в сетке линиями.
- Головоломки процедурно генерируются при помощи комбинации из солвера, генератора и оптимизатора.
- Солвер пытается решить головоломки так, как это делал бы человек, и присваивает каждой головоломке оценку интересности.
- Генератор головоломок создан таким образом, чтобы можно было с лёгкостью менять одну часть головоломки (числа) и при этом все остальные части (точки) менялись таким образом, чтобы головоломка оставалась решаемой.
- Оптимизатор головоломок многократно решает уровни и генерирует новые вариации из наиболее интересных, найденных на текущий момент.
Правила
Чтобы понять, как работает генератор уровней, нужно, к сожалению, разобраться с правилами игры. К счастью, они очень просты. Головоломка состоит из сетки, содержащей пустые квадраты, числа и точки. Пример:

Цель игрока — прочертить вертикальную или горизонтальную линию через каждое из чисел при соблюдении трёх условий:
- Линия, идущая через число, должна иметь ту же длину, что и число.
- Линии не могут пересекаться.
- Все точки необходимо закрыть линиями.
Пример решения:

Ура! Дизайн игры готов, UI реализован, и теперь единственное, что осталось — найти несколько сотен хороших головоломок. А для подобных игр обычно не имеет смысла пытаться создавать такие головоломки вручную. Это работа для компьютера.
Требования
Что делает головоломку для этой игры хорошей? Я склонен считать, что игры-головоломки можно разбить на две категории. Есть игры, в которых ты исследуешь сложное пространство состояний от начала до конца (например, Sokoban или Rush Hour), и в которых может быть и не очевидно, какие состояния существуют в игре. И есть игры, в которых все состояния известны с самого начала, и мы постепенно вылепливаем пространство состояний с помощью процесса устранения лишних (например, Sudoku или Picross). Моя игра определённо относится ко второй категории.
Игроки предъявляют очень отличающиеся требования к этим разным видам головоломок. Во втором случае они ожидают, что головоломку можно решить только дедукцией, и что им никогда не понадобится возврат назад/угадывание/процесс проб и ошибок[0][1].
Недостаточно знать, можно ли решить головоломку только с помощью логики. Кроме того, нам нужно как-то понять, насколько хороши создаваемые головоломки. В противном случае большинство уровней будет просто тривиальным шлаком. В идеальной ситуации этот принцип можно было использовать также для создания плавной кривой прогресса, чтобы при прохождении игроком игры уровни постепенно становились сложнее.
Солвер
Первый шаг к удовлетворению этих требований — создание солвера игры, оптимизированного для этой цели. Солвер грубого перебора с возвратом назад (backtracking) позволит быстро и точно определить, решаема ли головоломка; кроме того, его можно модифицировать, чтобы он определял, является ли решение уникальным. Но он не может дать представления о том, насколько сложна на самом деле головоломка, потому что люди решают их по-другому. Солвер должен имитировать поведение человека.
Как же человек решает эту головоломку? Вот пара очевидных ходов, которым учит внутриигровой туториал:
- Если точки можно достичь только из одного числа, то для закрытия точки нужно протянуть линию из этого числа. В этом примере точку можно достичь только из тройки, но не из четвёрки:
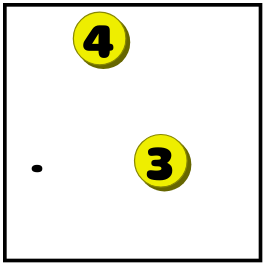
И это приводит к такой ситуации:

- Если линия не помещается в одном направлении, то её нужно расположить в другом. В показанном выше примере четвёрку больше нельзя расположить вертикально, поэтому мы знаем, что она будет горизонтальной:
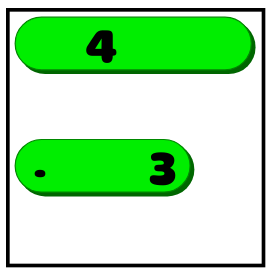
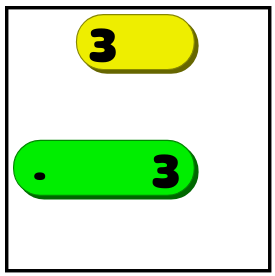
- Если известно, что линия длины X должна находиться в определённом положении (вертикаль/горизонталь) и недостаточно пустого пространства, чтобы разместить линию из X пустых клеток по обеим сторонам, то нужно покрыть несколько квадратов посередине. Если бы в показанном выше примере четвёрка была тройкой, то мы бы не знали, растягивается ли она до упора вправо или влево. Но мы бы знали, что линия должна закрывать два средних квадрата:
Подобные рассуждения — самая основа игры. Игрок ищет способы растянуть немного одну линию, а затем снова изучает поле, потому что оно может дать ему информацию, чтобы сделать ещё один логический вывод. Создания солвера, следующего этим правилам, будет достаточно, чтобы определить, сможет ли человек решить головоломку без возврата назад.
Однако это ничего не говорит нам о сложности или интересности уровня. Кроме решаемости, нам каким-то образом нужно численно оценить сложность.
Очевидная первая идея для функции оценки: чем больше ходов требуется для решения головоломки, тем она сложнее. Вероятно, в других играх это хорошая метрика, но моей, скорее всего, важнее количество допустимых ходов, которые есть у игрока. Если игрок может сделать 10 логических выводов, то он, скорее всего, найдёт один из них очень быстро. Если верный ход только один, то это потребует больше времени.
То есть в качестве первой аппроксимации нам нужно, чтобы дерево решений было глубоким и узким: есть длинная зависимость ходов от начала до конца, и в каждый момент времени есть только малое количество способов продвинуться вверх по цепочке[2].
Как нам определить ширину и глубину дерева? Однократное решение головоломки и оценка созданного дерева не дадут точного ответа. Точный порядок делаемых ходов влияет на форму дерева. Нам нужно рассмотреть все возможные решения и сделать с ними что-то вроде оптимизации по лучшим и худшим случаям. Мне знакома техника грубого перебора графов поиска в играх-головоломках, но для этого проекта я хотел создать однопроходной солвер, а не какой-то исчерпывающий поиск. Из-за фазы оптимизации я стремился к тому, чтобы время выполнения солвера измерялось не в секундах, а в миллисекундах.
Я решил этого не делать. Вместо этого мой солвер на самом деле не делает один ход за раз, а решает головоломку по слоям: взяв состояние, он находит все допустимые ходы, которые можно сделать. Затем применяет все эти ходы одновременно и начинает заново в новом состоянии. Количество слоёв и максимальное число ходов, найденное на одном слое, затем используются как приближенные значения глубины и ширины дерева поиска в целом.
Вот как при этой модели выглядит решение одной из сложных головоломок. Пунктирные линии — это линии, растянутые на этом слое солвера, сплошные — те, которые не менялись. Зелёные линии имеют правильную длину, красные ещё не завершены.

Следующая проблема заключается в том, что все делаемые игроком ходы создаются равными. То, что мы перечислили в начале этого раздела — просто здравый смысл. Вот пример более сложного правила дедукции, на поиск которого потребуется немного больше размышлений. Рассмотрим такое поле:

Точки в C и D можно покрыть только пятёркой и средней четвёркой (и ни одно число не может покрыть обе точки одновременно). Это значит, что четвёрка посередине должна покрыть одну точку из двух, а значит не может быть использовала для покрытия A. Следовательно, точку A должна закрыть четвёрка в левом нижнем углу.
Очевидно, что было бы глупо считать эту цепочку рассуждений равной простому выводу «этой точки можно достичь только из этого числа». Можно ли в функции оценки придавать этим более сложным правилам больший вес? К сожалению, в солвере на основе слоёв это невозможно, потому что в нём не гарантировано нахождение решения с наименьшими затратами. Это не только теоретическая проблема — на практике довольно часто бывает так, что часть поля решаема или единственным сложным рассуждением, или цепочкой гораздо более простых ходов. По сути, солвер на основе слоёв находит кратчайший, а не самый малозатратный путь, и это нельзя отразить в функции оценки.
В результате я пришёл к такому решению: я изменил солвер таким образом, чтобы каждый слой состоял только из одного типа рассуждений. Алгоритм обходит правила рассуждений в приблизительном порядке сложности. Если правило находит какие-то ходы, то они применяются, и на этом итерация завершается, а следующая итерация начинает список с самого начала.
Затем решению присваивается оценка: каждому слою назначаются затраты на основании одного правила, которое в нём использовалось. Это всё равно не гарантирует, что решение будет самым малозатратным, но при правильном подборе весов алгоритм хотя бы не будет находить затратное решение, если существует дешёвое.
Кроме того, это очень походит на то, как головоломки решают люди. Они сначала пытаются найти лёгкие решения, и начинают активно шевелить мозгами, только если простых ходов нет.
Генератор
Предыдущий раздел определял, хорош или плох конкретный уровень. Но только этого недостаточно, нам нужно ещё как-то сгенерировать уровни, чтобы солвер мог их оценить. Очень маловероятно, что случайно сгенерированный мир будет решаемым, не говоря уже об интересности.
Основная идея (она ни в коем случае не нова) заключается в попеременном использовании солвера и генератора. Давайте начнём с головоломки, которая, вероятно, нерешаема: просто расположим в случайных квадратах ячейки числа от двух до пяти:

Солвер работает до тех пор, пока не сможет дальше развиваться:

Затем генератор добавляет в головоломку ещё информации в виде точки, после чего продолжается выполнение солвера.

В этом случае добавленной точки солверу недостаточно для дальнейшего развития. Потом генератор будет продолжать добавлять новые точки, пока это не удовлетворит солвер:

А затем солвер продолжает свою обычную работу:

Этот процесс продолжается или пока головоломка не будет решена, или пока не останется больше информации для добавления (например, когда каждая клетка, которую можно достичь из числа, уже содержит точку).
Этот метод работает только в том случае, если добавляемая новая информация не может сделать неверными любые из ранее сделанных выводов. Это было бы сложно сделать при добавлении в сетку чисел[3]. Но добавление на поле новых точек обладает таким свойством; по крайней мере, для правил рассуждения, которые я использую в этой программе.
Куда алгоритм должен добавлять точки? В конце концов я решил добавлять их в пустое пространство, которое можно закрыть в начальном состоянии наибольшим количеством линий, чтобы каждая точка стремилась выдавать как можно меньше информации. Я не пытался специально разместить точку в том месте, где она была бы полезна для продвижения в решении головоломки на момент, когда солвер застрянет. Это создаёт очень удобный эффект: большинство точек кажется в начале головоломки совершенно бесполезными, из-за чего головоломка кажется сложнее, чем есть на самом деле. Если всё это множество очевидных ходов, которые может сделать игрок, но почему-то не один из них не срабатывает в должной мере. В результате получилось, что генератор головоломок ведёт себя немного по-свински.
Этот процесс не всегда создаёт решение, но он довольно быстр (порядка 50-100 миллисекунд), поэтому для генерации уровня можно просто повторить его несколько раз. К сожалению, обычно он создаёт посредственные головоломки. С самого начала есть слишком много очевидных ходов, поле заполняется очень быстро и дерево решений оказывается довольно неглубоким.
Оптимизатор
Описанный выше процесс создавал посредственные головоломки. На последнем этапе я использую эти уровни как основу для процесса оптимизации. Он работает следующим образом.
Оптимизатор создаёт пул, в котором содержится до 10 вариантов головоломки. Пул инициализируется новой сгенерированной случайной головоломкой. На каждой итерации оптимизатор выбирает из пула одну головоломку и выполняет её мутацию.
Мутация удаляет все точки, а затем немного изменяет числа (т.е. уменьшает/увеличивает значение случайно выбранного числа или перемещает число в другую клетку сетки). Можно применить к полю одновременно несколько мутаций. Затем мы запускаем солвер в специальном режиме генерации уровней, описанном в предыдущем разделе. Он добавляет в головоломку достаточное количество точек, чтобы она снова стала решаемой.
После этого мы снова запускаем солвер, на этот раз в обычном режиме. Во время этого прогона солвер отслеживает a) глубину дерева решений, b) частоту необходимости разных видов правил, c) ширину дерева решений в разные моменты времени. Головоломка оценивается на основании описанных выше критериев. Функция оценки предпочитает глубокие и узкие решения, а уровни повышенной сложности также придают больший вес головоломкам, в которых требуется использовать более сложные правила рассуждений.
Затем в пул добавляется новая головоломка. Если в пуле содержится больше 10 головоломок, то наихудшая отбрасывается.
Этот процесс повторяется несколько раз (меня устроило примерно 10000-50000 итераций). После этого версия головоломки с наибольшей оценкой сохраняется в базу данных уровней головоломки. Вот как выглядит прогресс наилучшей головоломки на протяжении одного прогона оптимизации:

Я пробовал использовать и другие способы структурирования оптимизации. В одной версии использовалась имитация отжига, другие были генетическими алгоритмами с различными операциями кроссинговера. Ни одно из решений не проявило себя так же хорошо, как наивный алгоритм с пулом восходящих к вершине вариантов.
Уникальное единственное решение
Когда головоломка имеет уникальное единственное решение, то возникает интересное затруднение. Можно ли допускать, чтобы игрок предполагал, что решение одно, и делал выводы исходя из этого? Будет ли честно, если генератор головоломок предположит, что игрок так и сделает?
В посте на HackerNews я говорил, что существует четыре варианта подхода к такой ситуации:
- Заявить о единственности решения с самого начала и заставить генератор, чтобы он создавал уровни, требующие такого вида рассуждений. Это плохое решение, потому что оно усложняет понимание правил. И обычно именно такие подробности люди забывают.
- Не гарантировать единственности решения: потенциально иметь множество решений и принимать их все. На самом деле это не решает проблему, а отодвигает её.
- Просто допустить, что это очень редкое событие, которое на практике не важно. (Именно такое решение использовалось в первоначальной реализации.)
- Изменить генератор головоломок таким образом, чтобы он не генерировал головоломки, в котором знание об уникальности решения помогало бы. (Вероятно, правильное решение, но требующее дополнительной работы.)
Изначально я выбрал последний вариант, и это было ужасной ошибкой. Оказалось, что я учёл только один способ, которым уникальность решения приводила к утечке информации, и он на самом деле довольно редок. Но есть и другие; один из них по сути присутствовал в каждом генерируемом мной уровне и часто приводил к тому, что решение становилось тривиальным. Поэтому в мае 2019 года я изменил режимы Hard и Expert, использовав третий вариант.
Самый раздражающий случай — это двойка с пунктирной линией на таком поле:

Почему хитрый игрок может сделать такой вывод? Двойка может закрывать любой из четырёх соседних квадратов. Ни в одном из них нет точек, поэтому они необязательно должны быть закрыты линией. А находящийся внизу квадрат не имеет наложений ни с какими другими числами. Если существует единственное решение, то это должен быть случай, когда другие числа закрывают остальные три квадрата, а двойка закрывает квадрат под ней.
Решение заключается в том, чтобы при распознавании таких случаев добавлять ещё несколько точек:

Ещё один распространённый случай — двойка с пунктиром на этом поле:

Квадраты слева и сверху от двойки ничем не отличаются. Ни в одном из них нет точки, и ни один нельзя достичь из любого другого числа. Любое решение, в котором двойка закрывает верхний квадрат, будет иметь соответствующее решение, в котором она закрывает левый квадрат, и наоборот. Если бы существовало единственное уникальное решение, то этого не могло бы быть, и двойка должна была закрывать нижний квадрат.
Подобный тип случаев я решил способом «если болит, то не трогай». Солвер применял это правило на раннем этапе в списке приоритетов и присваивал таким ходам большой отрицательный вес. Головоломки с такой особенностью обычно отбрасываются оптимизатором, а немногие оставшиеся отбрасываются на этапе окончательного выбора уровней для опубликованной игры.
Это не полный список, во время плейтестинга с намеренным поиском ошибок я нашёл множество других правил для уникальных решений. Но большинство из них казались редкими и их было довольно обнаружить, поэтому они не очень упрощали игру. Если кто-то решит головоломку, пользуясь подобными рассуждениями, то я не буду ставить это им в вину.
Заключение
Изначально игра разрабатывалась как эксперимент по процедурной генерации головоломок. Дизайн игры и генератор шли рука об руку, поэтому сами техники сложно применить напрямую в других играх.
Вопрос, на который у меня нет ответа: оправдало ли себя вложение таких усилий в процедурную генерацию? Отзывы игроков о дизайне уровней были очень противоречивыми. В положительных комментариях обычно говорилось о том, что в головоломках всегда ощущается какая-то хитрая уловка. В большинстве негативных отзывов мне писали, что в игре не достаёт градиента сложности.
У меня есть ещё пара головоломок в зачаточной стадии, и мне так понравился генератор, что скорее всего для них я использую подобный процедурный подход. Изменю я только одно: с самого начала буду проводить активный плейтестинг с поиском ошибок.
Примечания
[0] Или, по крайней мере, так мне казалось. Но когда я понаблюдал за игроками вживую, то почти половина из них просто делала догадки, а затем итеративно их прорабатывала. Ну да ладно.
[1] Читателям моей статьи также стоит прочитать статью Solving Minesweeper and making it better Магнуса Хоффа.
[2] Уточню, что глубина/узость дерева — это метрика, которую я посчитал значимой для своей игры, а не для всех других головоломок. Например, существует хороший аргумент о том, что головоломка Rush Hour интересна, если в ней есть несколько путей к решению почти, но не совсем одинаковой длины. Но так получилось потому, что Rush Hour — это игра на поиск кратчайшего решения, а не просто какого-нибудь решения.
[3] За исключением добавления единиц. В первой версии головоломки не было точек, и план заключался в том, чтобы при необходимости дополнительной информации генератор добавлял единицы. Но это казалось слишком ограничивающим.





