Привет, Хабр!
Мне давно хотелось добавлять в любые проекты Spring-анимации. Но делал я это только для React-проектов с помощью react-spring, так как не знал ничего другого.
Но наконец я решил разобраться, как оно все устроено и написать свою реализацию!
Если вы тоже хотите использовать Spring-анимации везде, заходите под кат. Там вы найдете немного теории, реализацию Spring на чистом JS и внедрение Spring-анимации во Vue с помощью компонентов и composition-api.

Реализация Spring-анимации на JS: https://playcode.io/590645/
Нужно добавить Spring-анимации в свой проект — возьмите Spring из библиотеки Popmotion.
Нужно добавить Spring-анимации в свой Vue-проект — возьмите Spring из библиотеки Popmotion и напишите себе обертку над ним.
Обычные css-анимации в вебе используют длительность и функцию расчета положения от времени.
Spring-анимации используют другой подход — физику пружины.
Для анимации мы задаем физические свойства системы: массу пружины, коэффициент упругости пружины, коэффициент трения среды. Затем мы растягиваем пружину на то расстояние, которое нам нужно проанимировать, и отпускаем ее.
Во фронтенд-проектах я вижу такие плюсы у Spring-анимаций:
1. Можно задать начальную скорость анимации
Если на сайте обрабатываются свайпы пальцами или перетаскивание мышкой, то анимации объектов будут выглядеть более натурально, если задать им начальную скорость как скорость свайпа или скорость мыши.

CSS-анимация, у которой не сохраняется скорость мыши

Spring-анимация, у которой пружине передается скорость мыши
2. Можно изменять конечную точку анимации
Если вы, например, хотите проанимировать объект до курсора мыши, то CSS'ом тут не поможешь — при обновлении положения курсора анимация инициализируется снова, из-за чего будет видно дерганье.
Со Spring-анимациями такой проблемы нет — если нужно поменять конечную точку анимации, то растягиваем или сжимаем пружину на нужный отступ.

Пример анимации элемента к курсору мыши; сверху — CSS-анимация, снизу — Spring-анимация
Возьмем обычную пружину с грузом. Она пока находится в состоянии покоя.
Потянем ее немного вниз. На пружину начинает действовать сила упругости (), которая стремится вернуть пружину в начальное положение. Когда мы отпустим пружину, она станет качаться по синусоиде:

Добавим силу трения. Пускай она будет прямо пропорциональна скорости пружины (). В таком случае колебания со временем станут затухать:
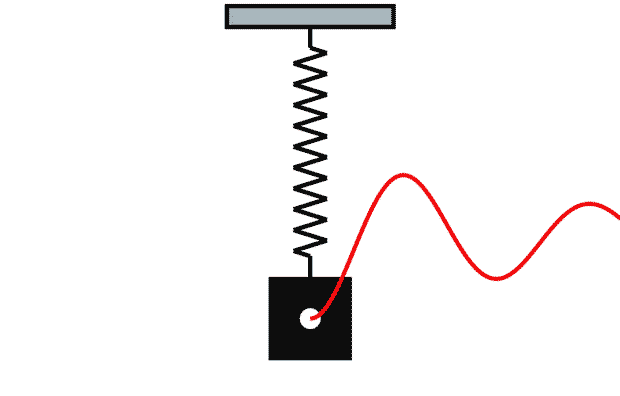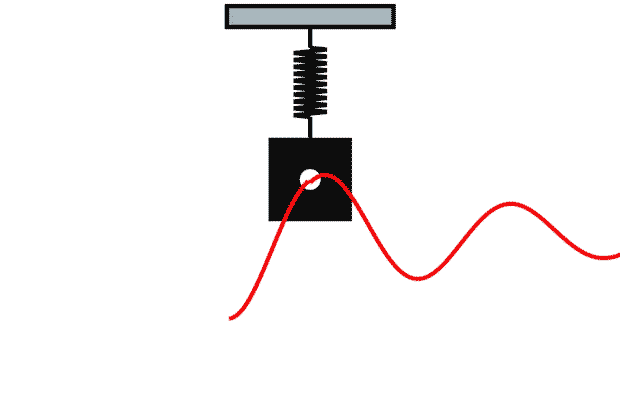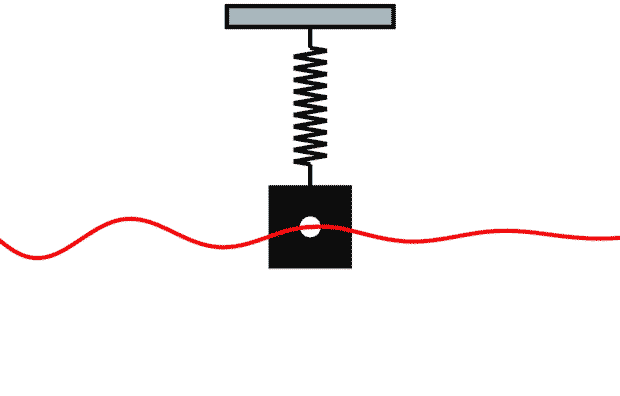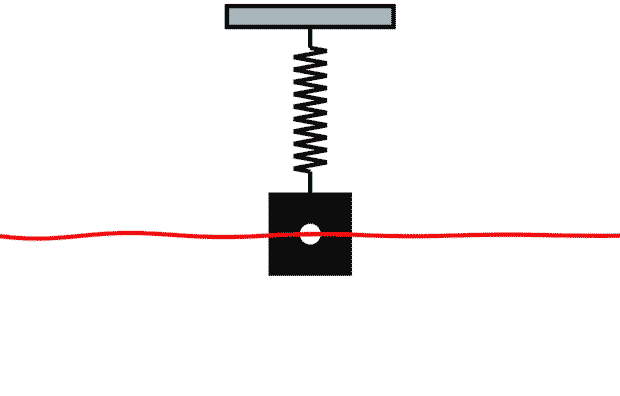
Мы хотим, чтобы наши Spring-анимации анимировались так же, как колеблется пружина при воздействии силы упругости и силы трения.
В контексте анимаций, разница между начальным и конечным значением анимации — это начальное растяжение пружины .
Перед началом анимации нам даны: масса пружины , коэффициент упругости пружины , коэффициент трения среды , растяжение пружины , начальная скорость .
Положение анимации рассчитывается несколько десятков раз в секунду. Временной интервал между расчетами анимации назовем .
Во время каждого нового расчета у нас есть скорость пружины и растяжение пружины на прошлом интервале анимации. Для первого расчета анимации , .
Начинаем считать положение анимации для интервала!
По второму закону Ньютона, сумма всех приложенных сил равна массе тела, умноженному на его ускорение:
На пружину действуют две силы — сила упругости и сила трения:
Распишем подробнее силы и найдем ускорение:
После этого мы можем найти новую скорость. Она равна сумме скорости на предыдущем интервале анимации и ускорению, умноженному на временной интервал:
Зная скорость, можно найти новое положение пружины:
Мы получили нужное положение, отображаем его пользователю!
Как только отобразили, начинаем новый интервал анимации. Для нового интервала , .
Анимацию стоит остановить, когда и становятся очень маленькими — в этот момент колебания пружины почти не видно.
У нас есть нужные формулы, осталось написать свою реализацию:
Песочница с кодом Spring-класса и примером его использования:
https://playcode.io/590645
С нашим классом Spring есть небольшая проблема — будет каждый раз разный при новых запусках анимации.
Откроете на старом мобильнике — будет равен 46 миллисекундам, нашему максимальному ограничению. Откроете на мощном компьютере — будет равняться 16-17 миллисекундам.
Меняющийся означает то, что длительность анимации и изменения анимируемого значения будут каждый раз немного разные.
Чтобы такого не происходило, можем поступить так:
Возьмем как фиксированное значение. При новом анимационном интервале мы должны будем вычислить, сколько времени прошло с прошлого интервала и сколько в нем фиксированных значений . Если время не делится без остатка на , то переносим остаток на следующий анимационный интервал.
Затем вычисляем и столько раз, сколько у нас получилось фиксированных значений. Последнее значение показываем пользователю.
Пример:
возьмем как 1 миллисекунда, между прошлым и новым анимационным интервалом прошло 32 миллисекунды.
Мы должны 32 раза рассчитать физику, и ; последний надо показать пользователю.
Вот так будет выглядеть метод doAnimationTick:
Таким методом расчета физики пользуется react-spring, в этой статьей можно прочитать подробнее.
Глядя на свойства системы — массу груза, коэффициент упругости и коэффициент трения среды — совсем непонятно, как ведет себя пружина. При создании Spring-анимаций эти переменные подбираются рандомно, пока программиста не удовлетворит «пружинистость» анимации.
Однако в физике для пружины с затуханием есть пара переменных, при взгляде на которые можно сказать, как ведет себя пружина.
Чтобы их найти, вернемся к нашему уравнению второго закона Ньютона:
Напишем его как дифференциальное уравнение:
Его можно переписать как:
где — частота колебаний пружины без учета силы трения, — коэффициент затухания.
Если решить это уравнение, то мы получим несколько функций , которые определяют положение пружины от времени. Решение сложу под спойлер, чтобы не растягивать статью слишком сильно, перейдем сразу к результату.
При мы получим уравнение, которое описывает затухающие колебания пружины. Чем меньше , тем ниже сила трения и больше видимых колебаний.
При мы получим уравнение с критическим трением, т.е. уравнение, при котором система возвращается к положению равновесия без колебаний, самым быстрым способом.
При мы получим уравнение, при котором система возвращается к положению равновесия без колебаний. Это будет происходить медленнее, чем при ; с увеличением уменьшается скорость схождения к положению равновесия.
Примеры анимаций при различных . Скорость анимации уменьшена в 4 раза
Помимо , есть еще одна понятная характеристика колебания пружины — период колебаний пружины без учета трения:
Мы получили два параметра:
→ , который определяет, насколько сильно анимация будет колебаться.
Возможные значения от 0 до 1.
Чем меньше , тем больше видимых колебаний будет у пружины. При 0 система не будет иметь силу трения, пружина будет колебаться без затухания; при 1 пружина будет сходиться к положению равновесия без колебаний.
Значения больше 1 нам не нужны — они работают как 1, только зря затягивают нашу анимацию.
→ , который будет говорить, насколько долго будет длиться анимация.
Стоит иметь в виду, параметр говорит о длительности одного колебания пружины без учета силы трения, а не об общей длительности анимации.
Теперь мы можем вывести коэффициент упругости и коэффициент трения среды, зная и и предполагая, что :
Реализуем эту логику в коде:
Теперь мы имеем метод getSpringValues, который принимает понятные для человека коэффициент затухания и период колебаний и возвращает массу пружины, коэффициент трения и коэффициент упругости.
Этот метод есть в песочнице по ссылке ниже, можете попробовать использовать его вместо обычных свойств системы:
https://playcode.io/590645
Чтобы удобно использовать Spring-анимации во Vue, можно поступить двумя способами: написать компонент-обертку или метод composition-api.
Давайте напишем компонент, который абстрагирует в себе использование Spring-класса.
Прежде чем писать его, представим как мы хотим его использовать:
Нам бы хотелось, чтобы:
Для полной функциональности компонент должен еще уметь изменять скорость пружины, но мы это не станем делать, чтобы не усложнять код.
Начинаем разработку:
Песочница с компонентом и примером его использования:
https://playcode.io/591686/
Для того, чтобы использовать composition-api, который появится во Vue 3.0, нам понадобится пакет composition-api.
Добавим его себе:
Теперь подумаем, каким бы мы хотели видеть наш метод для анимации:
Нам бы хотелось, чтобы:
Как и в случае с компонентом, не будем добавлять кастомизацию скорости пружины, чтобы не усложнять код.
Начинаем делать метод:
Песочница с методом composition-api и примером его использования:
https://playcode.io/591812/
В статье мы рассмотрели базовые особенности Spring-анимаций и внедрили их во Vue. Но у нас остался простор для доработок — во Vue-компоненты можно добавить возможность добавления новых полей после инициализации, добавить изменение скорости пружины.
Правда, писать в реальных проектах свой Spring совсем не обязательно: в библиотеке Popmotion уже есть готовая реализация Spring. Для Vue можно написать обертку, как мы сделали выше.
Спасибо, что дочитали до конца!
Мне давно хотелось добавлять в любые проекты Spring-анимации. Но делал я это только для React-проектов с помощью react-spring, так как не знал ничего другого.
Но наконец я решил разобраться, как оно все устроено и написать свою реализацию!
Если вы тоже хотите использовать Spring-анимации везде, заходите под кат. Там вы найдете немного теории, реализацию Spring на чистом JS и внедрение Spring-анимации во Vue с помощью компонентов и composition-api.

TL;DR
Реализация Spring-анимации на JS: https://playcode.io/590645/
Нужно добавить Spring-анимации в свой проект — возьмите Spring из библиотеки Popmotion.
Нужно добавить Spring-анимации в свой Vue-проект — возьмите Spring из библиотеки Popmotion и напишите себе обертку над ним.
Для чего нужны Spring-анимации
Обычные css-анимации в вебе используют длительность и функцию расчета положения от времени.
Spring-анимации используют другой подход — физику пружины.
Для анимации мы задаем физические свойства системы: массу пружины, коэффициент упругости пружины, коэффициент трения среды. Затем мы растягиваем пружину на то расстояние, которое нам нужно проанимировать, и отпускаем ее.
Во фронтенд-проектах я вижу такие плюсы у Spring-анимаций:
1. Можно задать начальную скорость анимации
Если на сайте обрабатываются свайпы пальцами или перетаскивание мышкой, то анимации объектов будут выглядеть более натурально, если задать им начальную скорость как скорость свайпа или скорость мыши.

CSS-анимация, у которой не сохраняется скорость мыши

Spring-анимация, у которой пружине передается скорость мыши
2. Можно изменять конечную точку анимации
Если вы, например, хотите проанимировать объект до курсора мыши, то CSS'ом тут не поможешь — при обновлении положения курсора анимация инициализируется снова, из-за чего будет видно дерганье.
Со Spring-анимациями такой проблемы нет — если нужно поменять конечную точку анимации, то растягиваем или сжимаем пружину на нужный отступ.

Пример анимации элемента к курсору мыши; сверху — CSS-анимация, снизу — Spring-анимация
Физика пружины
Возьмем обычную пружину с грузом. Она пока находится в состоянии покоя.
Потянем ее немного вниз. На пружину начинает действовать сила упругости (), которая стремится вернуть пружину в начальное положение. Когда мы отпустим пружину, она станет качаться по синусоиде:

Добавим силу трения. Пускай она будет прямо пропорциональна скорости пружины (). В таком случае колебания со временем станут затухать:

Мы хотим, чтобы наши Spring-анимации анимировались так же, как колеблется пружина при воздействии силы упругости и силы трения.
Считаем положение пружины для анимации
В контексте анимаций, разница между начальным и конечным значением анимации — это начальное растяжение пружины .
Перед началом анимации нам даны: масса пружины , коэффициент упругости пружины , коэффициент трения среды , растяжение пружины , начальная скорость .
Положение анимации рассчитывается несколько десятков раз в секунду. Временной интервал между расчетами анимации назовем .
Во время каждого нового расчета у нас есть скорость пружины и растяжение пружины на прошлом интервале анимации. Для первого расчета анимации , .
Начинаем считать положение анимации для интервала!
По второму закону Ньютона, сумма всех приложенных сил равна массе тела, умноженному на его ускорение:
На пружину действуют две силы — сила упругости и сила трения:
Распишем подробнее силы и найдем ускорение:
После этого мы можем найти новую скорость. Она равна сумме скорости на предыдущем интервале анимации и ускорению, умноженному на временной интервал:
Зная скорость, можно найти новое положение пружины:
Мы получили нужное положение, отображаем его пользователю!
Как только отобразили, начинаем новый интервал анимации. Для нового интервала , .
Анимацию стоит остановить, когда и становятся очень маленькими — в этот момент колебания пружины почти не видно.
Spring-анимация на JS
У нас есть нужные формулы, осталось написать свою реализацию:
class Spring {
constructor({ mass, tension, friction, initVelocity, from, to, onUpdate }) {
this.mass = mass; // Масса пружины
this.tension = tension; // Коэффициент упругости
this.friction = friction; // Коэффициент трения
this.initVelocity = initVelocity; // Начальная скорость
this.from = from; // От какого значения анимировать
this.to = to; // До какого значения анимировать
this.onUpdate = onUpdate; // Функция, вызывающаяся при обновлении значения
}
startAnimation() {
const callDoAnimationTick = () => {
const isFinished = this.doAnimationTick();
if (isFinished) {
return;
}
this.nextTick = window.requestAnimationFrame(callDoAnimationTick);
};
callDoAnimationTick();
}
stopAnimation() {
const { nextTick } = this;
if (nextTick) {
window.cancelAnimationFrame(nextTick);
}
this.isFinished = true;
}
doAnimationTick() {
const {
mass, tension, friction, initVelocity, from, to,
previousTimestamp, prevVelocity, prevValue, onUpdate,
} = this;
// Считаем Δt
const currentTimestamp = performance.now();
const deltaT = (currentTimestamp - (previousTimestamp || currentTimestamp))
/ 1000;
// Ограничим максимальный Δt 46 миллисекундами
const normalizedDeltaT = Math.min(deltaT, 0.046);
let prevSafeVelocity = prevVelocity || initVelocity || 0;
let prevSafeValue = prevValue || from;
// Считаем силу упругости, силу трения и ускорение
const springRestoringForce = -1 * tension * (prevSafeValue - to);
const dampingForce = -1 * prevSafeVelocity * friction;
const acceleration = (springRestoringForce + dampingForce) / mass;
// Считаем новую скорость и новое значение анимации
const newVelocity = prevSafeVelocity + acceleration * normalizedDeltaT;
const newValue = prevSafeValue + newVelocity * normalizedDeltaT;
// Проверяем анимацию на конец
const precision = 0.001;
const isFinished = Math.abs(newVelocity) < precision
&& Math.abs(newValue - to) < precision;
onUpdate({ value: newValue, isFinished });
this.previousTimestamp = currentTimestamp;
this.prevValue = newValue;
this.prevVelocity = newVelocity;
this.isFinished = isFinished;
return isFinished;
}
}
Песочница с кодом Spring-класса и примером его использования:
https://playcode.io/590645
Небольшое улучшение Spring-анимации
С нашим классом Spring есть небольшая проблема — будет каждый раз разный при новых запусках анимации.
Откроете на старом мобильнике — будет равен 46 миллисекундам, нашему максимальному ограничению. Откроете на мощном компьютере — будет равняться 16-17 миллисекундам.
Меняющийся означает то, что длительность анимации и изменения анимируемого значения будут каждый раз немного разные.
Чтобы такого не происходило, можем поступить так:
Возьмем как фиксированное значение. При новом анимационном интервале мы должны будем вычислить, сколько времени прошло с прошлого интервала и сколько в нем фиксированных значений . Если время не делится без остатка на , то переносим остаток на следующий анимационный интервал.
Затем вычисляем и столько раз, сколько у нас получилось фиксированных значений. Последнее значение показываем пользователю.
Пример:
возьмем как 1 миллисекунда, между прошлым и новым анимационным интервалом прошло 32 миллисекунды.
Мы должны 32 раза рассчитать физику, и ; последний надо показать пользователю.
Вот так будет выглядеть метод doAnimationTick:
class Spring {
/* ... */
doAnimationTick() {
const {
mass, tension, friction, initVelocity, from, to,
previousTimestamp, prevVelocity, prevValue, onUpdate,
} = this;
const currentTimestamp = performance.now();
const fractionalDiff = currentTimestamp - (previousTimestamp || currentTimestamp);
const naturalDiffPart = Math.floor(fractionalDiff);
const decimalDiffPart = fractionalDiff % 1;
const normalizedDiff = Math.min(naturalDiffPart, 46);
let safeVelocity = prevVelocity || initVelocity || 0;
let safeValue = prevValue || from;
// Рассчитываем физику для каждого 1-миллисекундного интервала
for (let i = 0; i < normalizedDiff; i++) {
const springRestoringForce = -1 * tension * (safeValue - to);
const dampingForce = -1 * safeVelocity * friction;
const acceleration = (springRestoringForce + dampingForce) / mass;
safeVelocity = safeVelocity + acceleration / 1000;
safeValue = safeValue + safeVelocity / 1000;
}
const precision = 0.001;
const isFinished = Math.abs(safeVelocity) < precision
&& Math.abs(safeValue - to) < precision;
onUpdate({ value: safeValue, isFinished });
// Отнимаем оставшуюся часть миллисекунды от текущего времени,
// так как мы ее не проанимировали
this.previousTimestamp = currentTimestamp - decimalDiffPart;
this.prevValue = safeValue;
this.prevVelocity = safeVelocity;
this.isFinished = isFinished;
return isFinished;
}
}
Таким методом расчета физики пользуется react-spring, в этой статьей можно прочитать подробнее.
Про коэффициент затухания и собственный период колебаний
Глядя на свойства системы — массу груза, коэффициент упругости и коэффициент трения среды — совсем непонятно, как ведет себя пружина. При создании Spring-анимаций эти переменные подбираются рандомно, пока программиста не удовлетворит «пружинистость» анимации.
Однако в физике для пружины с затуханием есть пара переменных, при взгляде на которые можно сказать, как ведет себя пружина.
Чтобы их найти, вернемся к нашему уравнению второго закона Ньютона:
Напишем его как дифференциальное уравнение:
Его можно переписать как:
где — частота колебаний пружины без учета силы трения, — коэффициент затухания.
Если решить это уравнение, то мы получим несколько функций , которые определяют положение пружины от времени. Решение сложу под спойлер, чтобы не растягивать статью слишком сильно, перейдем сразу к результату.
Решение уравнения
Кто хочет решить его сам, вот хорошее видео:
https://www.youtube.com/watch?v=uI2xt8nTOlQ
Нам дано линейное дифференциальное уравнение второго порядка:
Для его решения надо найти дискриминант у этого уравнения:
У данного уравнения будет три решения:
1. Решение при
мы получим при .
Общее решение линейного дифференциального уравнения второго порядка для выглядит так:
где — корни квадратного уравнения, написанного выше:
Получившееся решение:
где .
Получилась функция без гармонических колебаний, стремящаяся к 0.
2. Решение при
мы получим при .
Общее решение для выглядит так:
где — единственный корень квадратного уравнения, написанного выше:
Получившееся решение:
Получилась функция без гармонических колебаний, стремящаяся к 0. Она будет стремиться к нулю быстрее, чем при .
Правда, у меня не получилось придумать, как доказать, что эта функция сходится к 0 быстрее, чем при . Может, получится у вас в комментариях?
3. Решение при
мы получим при .
Общее решение для выглядит так:
и — это вещественная и мнимая части комплексных решений квадратного уравнения, написанного вначале:
Получившееся решение:
Получилось уравнение затухающих колебаний, стремящихся к 0.
Чем меньше , тем медленнее приближается к 0, т.е. будет больше видимых колебаний.
При затухания колебаний не будет.
https://www.youtube.com/watch?v=uI2xt8nTOlQ
Нам дано линейное дифференциальное уравнение второго порядка:
Для его решения надо найти дискриминант у этого уравнения:
У данного уравнения будет три решения:
1. Решение при
мы получим при .
Общее решение линейного дифференциального уравнения второго порядка для выглядит так:
где — корни квадратного уравнения, написанного выше:
Получившееся решение:
где .
Получилась функция без гармонических колебаний, стремящаяся к 0.
2. Решение при
мы получим при .
Общее решение для выглядит так:
где — единственный корень квадратного уравнения, написанного выше:
Получившееся решение:
Получилась функция без гармонических колебаний, стремящаяся к 0. Она будет стремиться к нулю быстрее, чем при .
Правда, у меня не получилось придумать, как доказать, что эта функция сходится к 0 быстрее, чем при . Может, получится у вас в комментариях?
3. Решение при
мы получим при .
Общее решение для выглядит так:
и — это вещественная и мнимая части комплексных решений квадратного уравнения, написанного вначале:
Получившееся решение:
Получилось уравнение затухающих колебаний, стремящихся к 0.
Чем меньше , тем медленнее приближается к 0, т.е. будет больше видимых колебаний.
При затухания колебаний не будет.
При мы получим уравнение, которое описывает затухающие колебания пружины. Чем меньше , тем ниже сила трения и больше видимых колебаний.
При мы получим уравнение с критическим трением, т.е. уравнение, при котором система возвращается к положению равновесия без колебаний, самым быстрым способом.
При мы получим уравнение, при котором система возвращается к положению равновесия без колебаний. Это будет происходить медленнее, чем при ; с увеличением уменьшается скорость схождения к положению равновесия.

Примеры анимаций при различных . Скорость анимации уменьшена в 4 раза
Помимо , есть еще одна понятная характеристика колебания пружины — период колебаний пружины без учета трения:
Мы получили два параметра:
→ , который определяет, насколько сильно анимация будет колебаться.
Возможные значения от 0 до 1.
Чем меньше , тем больше видимых колебаний будет у пружины. При 0 система не будет иметь силу трения, пружина будет колебаться без затухания; при 1 пружина будет сходиться к положению равновесия без колебаний.
Значения больше 1 нам не нужны — они работают как 1, только зря затягивают нашу анимацию.
→ , который будет говорить, насколько долго будет длиться анимация.
Стоит иметь в виду, параметр говорит о длительности одного колебания пружины без учета силы трения, а не об общей длительности анимации.
Теперь мы можем вывести коэффициент упругости и коэффициент трения среды, зная и и предполагая, что :
Реализуем эту логику в коде:
const getSpringValues = ({ dampingRatio, period }) => {
const mass = 1;
const tension = Math.pow(2 * Math.PI / period, 2);
const friction = 4 * Math.PI * dampingRatio / period;
return {
mass,
tension,
friction,
};
};
// Примеры использования
new Spring({
...getSpringValues({
dampingRatio: 0.3, // Пружина колеблется пару-тройку раз
period: 0.6, // Период колебания 600 мс
}),
from: 0,
to: 20,
onUpdate: () => { /* ... */ },
});
new Spring({
...getSpringValues({
dampingRatio: 1, // Пружина не колеблется
period: 0.2, // Период колебания 200 мс
}),
from: 0,
to: 20,
onUpdate: () => { /* ... */ },
});
Теперь мы имеем метод getSpringValues, который принимает понятные для человека коэффициент затухания и период колебаний и возвращает массу пружины, коэффициент трения и коэффициент упругости.
Этот метод есть в песочнице по ссылке ниже, можете попробовать использовать его вместо обычных свойств системы:
https://playcode.io/590645
Spring-анимация на Vue
Чтобы удобно использовать Spring-анимации во Vue, можно поступить двумя способами: написать компонент-обертку или метод composition-api.
Spring-анимация через компонент
Давайте напишем компонент, который абстрагирует в себе использование Spring-класса.
Прежде чем писать его, представим как мы хотим его использовать:
<template>
<div>
<SpringWrapper
:mass="1"
:tension="170"
:friction="14"
:animationProps="{ x, y }"
:animate="true"
v-slot="{ x: newX, y: newY }"
>
<div :style="{ transform: `translate(${newX}px, ${newY}px)` }" />
</SpringWrapper>
</div>
</template>
<script>
import SpringWrapper from 'path/to/SpringWrapper';
export default {
components: {
SpringWrapper,
},
data() {
return {
x: 0,
y: 0,
};
},
mounted() {
setTimeout(() => {
this.x = 100;
this.y = 100;
}, 1000);
},
};
</script>
Нам бы хотелось, чтобы:
- Можно было задать свойства пружины
- В параметре animationProps можно было указать те поля, которые мы хотим проанимировать
- В параметре animate передавалось значение, надо ли анимировать animationProps
- При любом изменении полей в animationProps они менялись с помощью Spring-анимации и передавались внутрь scoped-слота
Для полной функциональности компонент должен еще уметь изменять скорость пружины, но мы это не станем делать, чтобы не усложнять код.
Начинаем разработку:
const SpringWrapper = {
props: {
friction: { type: Number, default: 10 },
tension: { type: Number, default: 270 },
mass: { type: Number, default: 1 },
animationProps: { type: Object, required: true },
animate: { type: Boolean, required: true },
},
data: () => ({
// Объект с анимированными значениями
actualAnimationProps: null,
}),
created() {
this.actualAnimationProps = this.animationProps;
// Объект, в котором будут храниться Spring-объекты
this._springs = {};
},
watch: {
animationProps: {
deep: true,
// Обрабатываем любое изменение animationProps
handler(animationProps) {
const {
friction, tension, mass,
animate, actualAnimationProps, _springs,
} = this;
// Если не нужно анимировать поля, то сразу задаем их
if (!animate) {
this.actualAnimationProps = animationProps;
return;
}
// Проходимся по каждому полю для анимации
Object.entries(animationProps).forEach((([key, value]) => {
const _spring = _springs[key];
const actualValue = actualAnimationProps[key];
// Если у нас уже был Spring-объект,
// то растягиваем его до нужного значения
if (_spring && !_spring.isFinished) {
_spring.to = value;
return;
}
const spring = new Spring({
friction,
tension,
mass,
initVelocity: 0,
from: actualValue,
to: value,
onUpdate: ({ value }) => {
actualAnimationProps[key] = value;
},
});
spring.startAnimation();
_springs[key] = spring;
}));
}
},
animate(val) {
const { _springs } = this;
// Если нужно перестать анимировать поля,
// то выключаем все Spring-анимации
if (!val) {
Object.values(_springs).forEach((spring) => {
spring.stopAnimation();
})
this.actualAnimationProps = this.animationProps;
}
},
},
render() {
const { $scopedSlots, actualAnimationProps } = this;
// Передаем проанимированные значения в scopedSlot
return $scopedSlots.default(actualAnimationProps)[0];
},
};
Песочница с компонентом и примером его использования:
https://playcode.io/591686/
Spring-анимация через метод composition-api
Для того, чтобы использовать composition-api, который появится во Vue 3.0, нам понадобится пакет composition-api.
Добавим его себе:
npm i @vue/composition-api
import Vue from 'vue'
import VueCompositionApi from '@vue/composition-api';
Vue.use(VueCompositionApi);
Теперь подумаем, каким бы мы хотели видеть наш метод для анимации:
<template>
<div>
<div :style="{ transform: `translate(${x}px, ${y}px)` }" />
</div>
</template>
<script>
import useSpring from 'path/to/useSpring';
export default {
setup() {
const { x, y, animate } = useSpring({
mass: 1,
tension: 170,
friction: 10,
x: 0,
y: 0,
});
setTimeout(() => {
x.value = 100;
y.value = 100;
}, 1000);
return {
x,
y,
animate,
};
},
};
</script>
Нам бы хотелось, чтобы:
- Можно было задать свойства пружины
- Функция принимала на вход объект с полями, которые мы хотим проанимировать
- Функция возвращала computed-обертки. Setter'ы будут принимать на вход значения, которые мы хотим проанимировать; getter'ы будут возвращать проанимированное значение
- Функция возвращала animate-переменную, которая будет отвечать за то, надо нам проигрывать анимацию или нет
Как и в случае с компонентом, не будем добавлять кастомизацию скорости пружины, чтобы не усложнять код.
Начинаем делать метод:
import { reactive, computed, ref, watch } from '@vue/composition-api';
import { Spring } from '@cag-animate/core';
const useSpring = (initialProps) => {
const {
mass, tension, friction,
animate: initialAnimate,
...restInitialProps
} = initialProps;
// Создаем объект, в котором будут храниться проанимированные значения
const actualProps = reactive(restInitialProps);
const springs = {};
const mirrorProps = {};
Object.keys(initialProps).forEach(key => {
// Для каждой переменной создаем computed-обертку
//
// Getter возвращает проанимированное значение из actualProps
// Setter запускает Spring-анимацию
mirrorProps[key] = computed({
get: () => actualProps[key],
set: val => {
const _spring = springs[key];
const actualValue = actualProps[key];
if (!mirrorProps.animate.value) {
actualProps[key] = val;
return
}
if (_spring && !_spring.isFinished) {
_spring.to = val;
return;
}
const spring = new Spring({
friction,
tension,
mass,
initVelocity: 0,
from: actualValue,
to: val,
onUpdate: ({ value }) => {
actualProps[key] = value;
},
});
spring.startAnimation();
springs[key] = spring;
},
});
});
mirrorProps.animate = ref(initialAnimate || true);
watch(() => mirrorProps.animate.value, (val) => {
if (!val) {
Object.entries(springs).forEach(([key, spring]) => {
spring.stopAnimation();
actualProps[key] = spring.to;
});
}
});
return mirrorProps;
};
export default useSpring;
Песочница с методом composition-api и примером его использования:
https://playcode.io/591812/
Последнее слово
В статье мы рассмотрели базовые особенности Spring-анимаций и внедрили их во Vue. Но у нас остался простор для доработок — во Vue-компоненты можно добавить возможность добавления новых полей после инициализации, добавить изменение скорости пружины.
Правда, писать в реальных проектах свой Spring совсем не обязательно: в библиотеке Popmotion уже есть готовая реализация Spring. Для Vue можно написать обертку, как мы сделали выше.
Спасибо, что дочитали до конца!
Использованные материалы
- react-spring
- Demystifying UIKit Spring Animations
- Harmonic oscillator