Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Компания SpaceX, основанная небезызвестным Илон Маск, выпустила симулятор ручной стыковки корабля Crew Dragon с МКС. Если все пойдет по плану, стыковку проведут 27 мая 2020 года. Она будет проходить в полностью автоматическом режиме, но экипаж корабля сможет переключиться на ручное управление. Собственно, именно ручной режим и воспроизведен в симуляторе.
Сам симулятор расположен на сайте сайте и представляет собой, довольно проблематичную, на первый взгряд игрушку…
Космический челнок так и норовит улететь не туда… А точность с которой нужно попасть в шлюз составляет 20 см… по трем осям, а также по угловой скорости, скорости смещения и т.д.
Во мне заиграли патриотичные чувства и как-то стало обидно, за бывшую космическую державу, и я принял этот симулятор как вызов. Раз Маск решил показать сложность стыковки, и какие сложности их инженеры проходили, чтобы сделать программу автоматической стыковки, я решил написать, в свободное от работы время, программу на JavaScript, которая с легкостью состыкует Dragon и МКС в этом симуляторе.
Как тебе такое Илон Маск?

— Для начала немного истории.
Широко известный факт, что наш многоразовый космический корабль «Буран» был очень похож на американский челнок. А так же известно, что он летал всего только один раз, в отличии от американских «аналогов». Но мало кто знает, что его единственный полет был беспилотным. Он сам взлетел, сам приземлился и все это он сделал в очень плохие погодные условия. Американские Шатлы всегда приземлялись только в ручном режиме. Это было удивительно, принимая во внимание тот факт, что компьютеры раньше были не мощнее калькулятора. То, в теории, это не должно быть сложно, — подумал вчера вечером.
— Но дайте перейдем к сути. Что представляет собой симулятор на сайте SpaceX.
На старте мы видим общую информацию, что отклонение по всем параметрам должно быть в пределах 0.2 метра (20 см). Учитывая размеры станции и корабля, это довольно серьезное ограничение.
Запускаем симулятор и видим.

Сверху, справа и снузу центральной окружности — уговое отклонение коробля по трем осям.
Зеленым — текущее значение.
Синие — скорость в секунду с которым оно измениятся.
Слева смещение относительно, шлюза в метрах. Скорости смещения нет…
Контролёры управления внизу экрана представляют собой кнопки с дублированием их на клавиатуре.
Вот с них и начнем разбор программы, как наименее интересных.
Схема клавиатурных кнопок.

Левый блок отвечает за смещение относительно шлюза, а вот правый за смещение относительно осей.
Пишем, или находим в сети код, который умеет эмулировать клавиатруные нажатие на document. В моем случае код выглядел так.
Запишем коды кнопок:
Любая система управления подразумевает работу в цикле. Сделаем его наиболее простым, с шагом в 200 миллисекунд. За одно организуем счетчик, он нам еще понадобится.
Вернемся к структуре сайта.
Его интересной особенностью является, что МКС рисуется на канвасе, а вот информация о состоянии нашего космического корабля нарисованы обычной разметкой. Такое чувство, что разработчики сайта предполагали, что найдутся подобные энтузиасты, кто захочет «автоматизировать» игру и дали им такую возможность… А может разметкой, было сделать, тупо, проще.
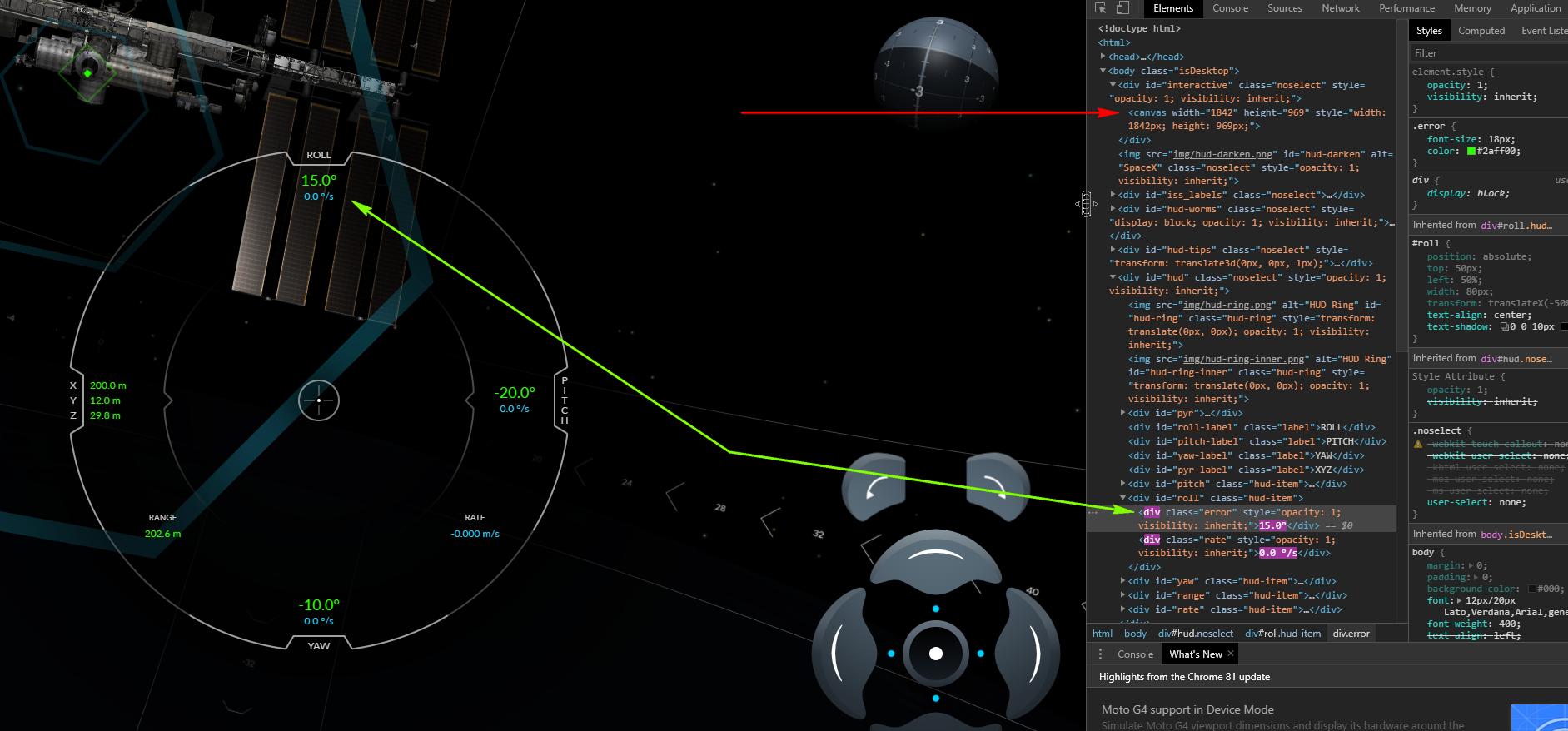
И так, допишем еще пару легких строк, дабы вытащить информацию о состоянии нашего космического аппарата.
Как можно заметить я вытащил далеко не всё. Я вытащил только значения смещения, но скорость изменения значений брать не стал и вот почему…
На самом деле, это уже третья итерация алгоритма. Сначала он представляя собой простой, который каждый 200 миллисекунд берет информацию о состоянии корабля и подгоняет его под 0.
Выглядело это так.
И на самом деле он вполне был рабочий. Особенно для угловых смещений. А для смещения по осям я использовал такой вариант.
Скорость смещения корабля относительно каждой из осей на экран не выводится, но её не сложно подсчитать.
И получалось довольно сносно. Классическая схема управления с обратной связью. И пока корабль был на удалении от МКС мы летели себе вполне ровненько [так мне тогда казалось]. Но проблемы начинались возле самого корабля. На самом деле корабль сильно колбасило и попасть с точностью 0.2 метра было физически невозможно. Дело в том, что смешение нашего корабля происходило… скажем так в непрерывном пространстве (с большой точностью), а вот мы видели лишь десятые доли от этого. И естественно, пытаясь реагировать на них каждые 200 миллисекунд, у нас получалось очень сильные действия по регулированию. Мы слишком много раз «тыкали на кнопки» при малейшем отклонении. А чем ближе к кораблю, тем сильнее значения смещения начинали скакать и мы фактически еще больше раскачивали корабль… Увеличивая амплитуду его движения…
Нужно было где-то взять недостающую точность. Во второй итерации в решении данной задачи, я сам постарался посчитать уже только на основе смещения скорости. И да, так вроде тоже получалось неплохо, но это не решило проблему с движением…
А в чем суть проблемы движения? Ну смотрите, мы находим в космическом пространстве и нажимая на кнопки управление придаём ускорение кораблю в той или иной плоскости. Но как только мы отпускаем кнопку движение не прекращается. В космическом пространстве, в связи с вакуумом, нет никакого сопротивления. И как только мы придали импульс (нажатием кнопки) корабль начал движение с этой скоростью… И его нужно как-то остановить. Остановить в симуляторе довольно легко – нужно дать обратный импульс.
Но на второй итерации решения, увеличенная точность ошибки не давала мне ответа о том, как мне корректировать скорость…
И вот здесь нам и потребовался «циркуль». Капитан любого корабля/судна должен рассчитывать маршрут заранее. Если он даст команду сбросить скорость после того как войдет в порт, то вряд ли он ювелирно пришвартуется. А нам, как раз, это и нужно.
Нам нужно рассчитать маршрут, капитаны обычно это делают с помощью циркуля с дискретным состоянием его наконечников. И сделаем тоже самое. Будем рассчитывать маршрут на секунду вперед, которая будет включать в себя пять итераций нажатий на кнопки ну или не будет…
Функция carculatePath, исходя их текущего значения отклонении, рассчитывает 5 шагов которые по идее должны это уклонение свести к 0. Необязательно на этой итерации, но каждый раз мы должны приближаться к заветному нулю в свой собственной более детальной сетке.
Собственно всё, мы рассчитываем маршрут каждую «равную» секунду (index % 5 === 0) и теперь нужно просто идти этим курсом.
Единственный расчет, который уцелел еще с первой итерации, это сближение с кораблем.
Тут довольно всё, хорошо, мы, на относительно малом ходу, движемся вперед
Под спойлером полный код. Вы можете сами проверить его работоспособность на сайте iss-sim.spacex.com
Собственно все. Всем спасибо за прочтение :)
П.С.
Да я немного хайпанул и поприкалывался. Не воспринимайте статью всерьез, я хотел почувствовать себя космонавтом, как Гагарин Юрий Алексеевич… Хотя это скорее инженерная работа Королёва Сергея Павловича, который к сожалению, так и не побывал в космосе, о котором мечтал…
Сам симулятор расположен на сайте сайте и представляет собой, довольно проблематичную, на первый взгряд игрушку…
Космический челнок так и норовит улететь не туда… А точность с которой нужно попасть в шлюз составляет 20 см… по трем осям, а также по угловой скорости, скорости смещения и т.д.
Во мне заиграли патриотичные чувства и как-то стало обидно, за бывшую космическую державу, и я принял этот симулятор как вызов. Раз Маск решил показать сложность стыковки, и какие сложности их инженеры проходили, чтобы сделать программу автоматической стыковки, я решил написать, в свободное от работы время, программу на JavaScript, которая с легкостью состыкует Dragon и МКС в этом симуляторе.
Как тебе такое Илон Маск?

Внимание! Данный алгоритм является «стебным», и не предназначал для использования его в реальных условиях. Автор не несет ответственности за любые прямые или косвенные убытки, нанесенные вашему космическому короблю или иным объектам при использовании данного алгоритма.
— Для начала немного истории.
Широко известный факт, что наш многоразовый космический корабль «Буран» был очень похож на американский челнок. А так же известно, что он летал всего только один раз, в отличии от американских «аналогов». Но мало кто знает, что его единственный полет был беспилотным. Он сам взлетел, сам приземлился и все это он сделал в очень плохие погодные условия. Американские Шатлы всегда приземлялись только в ручном режиме. Это было удивительно, принимая во внимание тот факт, что компьютеры раньше были не мощнее калькулятора. То, в теории, это не должно быть сложно, — подумал вчера вечером.
— Но дайте перейдем к сути. Что представляет собой симулятор на сайте SpaceX.
На старте мы видим общую информацию, что отклонение по всем параметрам должно быть в пределах 0.2 метра (20 см). Учитывая размеры станции и корабля, это довольно серьезное ограничение.
Запускаем симулятор и видим.

Сверху, справа и снузу центральной окружности — уговое отклонение коробля по трем осям.
Зеленым — текущее значение.
Синие — скорость в секунду с которым оно измениятся.
Слева смещение относительно, шлюза в метрах. Скорости смещения нет…
Контролёры управления внизу экрана представляют собой кнопки с дублированием их на клавиатуре.
Вот с них и начнем разбор программы, как наименее интересных.
Схема клавиатурных кнопок.

Левый блок отвечает за смещение относительно шлюза, а вот правый за смещение относительно осей.
Пишем, или находим в сети код, который умеет эмулировать клавиатруные нажатие на document. В моем случае код выглядел так.
function simulateKey(keyCode, type, modifiers) {
var evtName = (typeof (type) === "string") ? "key" + type : "keydown";
var modifier = (typeof (modifiers) === "object") ? modifier : {};
var event = document.createEvent("HTMLEvents");
event.initEvent(evtName, true, false);
event.keyCode = keyCode;
for (var i in modifiers) {
event[i] = modifiers[i];
}
document.dispatchEvent(event);
}
function keyPress(keyCode) {
simulateKey(keyCode)
setTimeout(() => simulateKey(keyCode, "up"), 15);
}
Запишем коды кнопок:
let _accelerator = 69;
let _brake = 81;
let _translateLeft = 65;
let _translateRigth = 68;
let _translateUp = 87;
let _translateDown = 83;
let _left = 37;
let _rigth = 39;
let _up = 38;
let _down = 40;
let _rollRigth = 105;
let _rollLeft = 103;Любая система управления подразумевает работу в цикле. Сделаем его наиболее простым, с шагом в 200 миллисекунд. За одно организуем счетчик, он нам еще понадобится.
let index = 0;
function A() {
index++;
setTimeout(A, 200);
}
A();
Вернемся к структуре сайта.
Его интересной особенностью является, что МКС рисуется на канвасе, а вот информация о состоянии нашего космического корабля нарисованы обычной разметкой. Такое чувство, что разработчики сайта предполагали, что найдутся подобные энтузиасты, кто захочет «автоматизировать» игру и дали им такую возможность… А может разметкой, было сделать, тупо, проще.

И так, допишем еще пару легких строк, дабы вытащить информацию о состоянии нашего космического аппарата.
let range = parseFloat($("#range .rate").outerText.split(' '));
let yDistance = parseFloat($("#y-range .distance").outerText.split(' ')[0]);
let zDistance = parseFloat($("#z-range .distance").outerText.split(' ')[0]);
let rollError = parseFloat($("#roll .error").outerText);
let pitchError = parseFloat($("#pitch .error").outerText);
let yawError = parseFloat($("#yaw .error").outerText);
let rate = parseFloat($("#rate .rate").outerText.split(' ')[0]);Как можно заметить я вытащил далеко не всё. Я вытащил только значения смещения, но скорость изменения значений брать не стал и вот почему…
На самом деле, это уже третья итерация алгоритма. Сначала он представляя собой простой, который каждый 200 миллисекунд берет информацию о состоянии корабля и подгоняет его под 0.
Выглядело это так.
if (rollError !== -rollSpeed) {
const rollLimit = (Math.abs(rollError) / 10);
if (0 < rollError && rollSpeed < rollLimit) {
keyPress(_rollRigth);
} else if (rollError < -0 && -rollLimit < rollSpeed) {
keyPress(_rollLeft);
}
}И на самом деле он вполне был рабочий. Особенно для угловых смещений. А для смещения по осям я использовал такой вариант.
const zLimit = (Math.abs(yawError) / 10);
if (0 < zDistance && zSpeed < zLimit) {
keyPress(_translateDown);
} else if (zDistance < 0 && -1 < zSpeed) {
keyPress(_translateUp);
}Скорость смещения корабля относительно каждой из осей на экран не выводится, но её не сложно подсчитать.
function carculateSpeed() {
let yDistance = parseFloat($("#y-range .distance").outerText.split(' ')[0]);
let zDistance = parseFloat($("#z-range .distance").outerText.split(' ')[0]);
ySpeed = yPrev - yDistance;
yPrev = yDistance;
zSpeed = zPrev - zDistance;
zPrev = zDistance;
setTimeout(carculateSpeed, 1000);
}
carculateSpeed();И получалось довольно сносно. Классическая схема управления с обратной связью. И пока корабль был на удалении от МКС мы летели себе вполне ровненько [так мне тогда казалось]. Но проблемы начинались возле самого корабля. На самом деле корабль сильно колбасило и попасть с точностью 0.2 метра было физически невозможно. Дело в том, что смешение нашего корабля происходило… скажем так в непрерывном пространстве (с большой точностью), а вот мы видели лишь десятые доли от этого. И естественно, пытаясь реагировать на них каждые 200 миллисекунд, у нас получалось очень сильные действия по регулированию. Мы слишком много раз «тыкали на кнопки» при малейшем отклонении. А чем ближе к кораблю, тем сильнее значения смещения начинали скакать и мы фактически еще больше раскачивали корабль… Увеличивая амплитуду его движения…
Нужно было где-то взять недостающую точность. Во второй итерации в решении данной задачи, я сам постарался посчитать уже только на основе смещения скорости. И да, так вроде тоже получалось неплохо, но это не решило проблему с движением…
А в чем суть проблемы движения? Ну смотрите, мы находим в космическом пространстве и нажимая на кнопки управление придаём ускорение кораблю в той или иной плоскости. Но как только мы отпускаем кнопку движение не прекращается. В космическом пространстве, в связи с вакуумом, нет никакого сопротивления. И как только мы придали импульс (нажатием кнопки) корабль начал движение с этой скоростью… И его нужно как-то остановить. Остановить в симуляторе довольно легко – нужно дать обратный импульс.
Но на второй итерации решения, увеличенная точность ошибки не давала мне ответа о том, как мне корректировать скорость…
И вот здесь нам и потребовался «циркуль». Капитан любого корабля/судна должен рассчитывать маршрут заранее. Если он даст команду сбросить скорость после того как войдет в порт, то вряд ли он ювелирно пришвартуется. А нам, как раз, это и нужно.
Нам нужно рассчитать маршрут, капитаны обычно это делают с помощью циркуля с дискретным состоянием его наконечников. И сделаем тоже самое. Будем рассчитывать маршрут на секунду вперед, которая будет включать в себя пять итераций нажатий на кнопки ну или не будет…
if (index % 5 === 0) {
calculatePath(roll, rollError);
calculatePath(pitch, pitchError);
calculatePath(yaw, yawError);
calculatePath(y, yDistance);
calculatePath(z, zDistance);
}Функция carculatePath, исходя их текущего значения отклонении, рассчитывает 5 шагов которые по идее должны это уклонение свести к 0. Необязательно на этой итерации, но каждый раз мы должны приближаться к заветному нулю в свой собственной более детальной сетке.
function calculatePath(data, value) {
data.path = [];
if (data.prev === value) {
data.speed = 0;
}
for (let i = 0; i < 5; i++) {
if (0 < value + data.speed * (i + 1)) {
data.speed -= 0.1;
data.path.push(-1);
} else if (value + data.speed * (i + 1) < -0) {
data.speed += 0.1;
data.path.push(1);
} else if (i > 0) {
if (0 < data.speed) {
data.speed -= 0.1;
data.path.push(-1);
} else if (data.speed < 0) {
data.speed += 0.1;
data.path.push(1);
} else {
data.path.push(0);
}
} else {
data.path.push(0);
}
}
data.prev = value;
}Собственно всё, мы рассчитываем маршрут каждую «равную» секунду (index % 5 === 0) и теперь нужно просто идти этим курсом.
let rollStep = roll.path[index % 5];
if (0 < rollStep) {
keyPress(_rollLeft);
} else if (rollStep < 0) {
keyPress(_rollRigth);
}
let pitchStep = pitch.path[index % 5];
if (0 < pitchStep) {
keyPress(_up);
} else if (pitchStep < 0) {
keyPress(_down);
}
let yawStep = yaw.path[index % 5];
if (0 < yawStep) {
keyPress(_left);
} else if (yawStep < 0) {
keyPress(_rigth);
}
let yStep = y.path[index % 5];
if (0 < yStep) {
keyPress(_translateRigth);
} else if (yStep < 0) {
keyPress(_translateLeft);
}
let zStep = z.path[index % 5];
if (0 < zStep) {
keyPress(_translateUp);
} else if (zStep < 0) {
keyPress(_translateDown);
}Единственный расчет, который уцелел еще с первой итерации, это сближение с кораблем.
Тут довольно всё, хорошо, мы, на относительно малом ходу, движемся вперед
const rangeLimit = Math.min(Math.max((Math.abs(range) / 100), 0.05), 2);
if (-rate < rangeLimit) {
keyPress(_accelerator);
} else if (-rangeLimit < -rate) {
keyPress(_brake);
}
Под спойлером полный код. Вы можете сами проверить его работоспособность на сайте iss-sim.spacex.com
Полный код
function simulateKey(keyCode, type, modifiers) {
var evtName = (typeof (type) === "string") ? "key" + type : "keydown";
var modifier = (typeof (modifiers) === "object") ? modifier : {};
var event = document.createEvent("HTMLEvents");
event.initEvent(evtName, true, false);
event.keyCode = keyCode;
for (var i in modifiers) {
event[i] = modifiers[i];
}
document.dispatchEvent(event);
}
function keyPress(keyCode) {
simulateKey(keyCode)
setTimeout(() => simulateKey(keyCode, "up"), 15);
}
let _accelerator = 69;
let _brake = 81;
let _translateLeft = 65;
let _translateRigth = 68;
let _translateUp = 87;
let _translateDown = 83;
let _left = 37;
let _rigth = 39;
let _up = 38;
let _down = 40;
let _rollRigth = 105;
let _rollLeft = 103;
let index = 0;
roll = {
path: [0, 0, 0, 0, 0],
prev: 0,
speed: 0,
}
pitch = {
path: [0, 0, 0, 0, 0],
prev: 0,
speed: 0,
}
yaw = {
path: [0, 0, 0, 0, 0],
prev: 0,
speed: 0,
}
z = {
path: [0, 0, 0, 0, 0],
prev: 0,
speed: 0,
}
y = {
path: [0, 0, 0, 0, 0],
prev: 0,
speed: 0,
}
function carculatePath(data, value) {
data.path = [];
if (data.prev === value) {
data.speed = 0;
}
for (let i = 0; i < 5; i++) {
if (0 < value + data.speed * (i + 1)) {
data.speed -= 0.1;
data.path.push(-1);
} else if (value + data.speed * (i + 1) < -0) {
data.speed += 0.1;
data.path.push(1);
} else if (i > 0) {
if (0 < data.speed) {
data.speed -= 0.1;
data.path.push(-1);
} else if (data.speed < 0) {
data.speed += 0.1;
data.path.push(1);
} else {
data.path.push(0);
}
} else {
data.path.push(0);
}
}
data.prev = value;
}
function A() {
let range = parseFloat($("#range .rate").outerText.split(' '));
let yDistance = parseFloat($("#y-range .distance").outerText.split(' ')[0]);
let zDistance = parseFloat($("#z-range .distance").outerText.split(' ')[0]);
let rollError = parseFloat($("#roll .error").outerText);
let pitchError = parseFloat($("#pitch .error").outerText);
let yawError = parseFloat($("#yaw .error").outerText);
let rate = parseFloat($("#rate .rate").outerText.split(' ')[0]);
if (index % 5 === 0) {
carculatePath(roll, rollError);
carculatePath(pitch, pitchError);
carculatePath(yaw, yawError);
carculatePath(y, yDistance);
carculatePath(z, zDistance);
}
let rollStep = roll.path[index % 5];
if (0 < rollStep) {
keyPress(_rollLeft);
} else if (rollStep < 0) {
keyPress(_rollRigth);
}
let pitchStep = pitch.path[index % 5];
if (0 < pitchStep) {
keyPress(_up);
} else if (pitchStep < 0) {
keyPress(_down);
}
let yawStep = yaw.path[index % 5];
if (0 < yawStep) {
keyPress(_left);
} else if (yawStep < 0) {
keyPress(_rigth);
}
let yStep = y.path[index % 5];
if (0 < yStep) {
keyPress(_translateRigth);
} else if (yStep < 0) {
keyPress(_translateLeft);
}
let zStep = z.path[index % 5];
if (0 < zStep) {
keyPress(_translateUp);
} else if (zStep < 0) {
keyPress(_translateDown);
}
const rangeLimit = Math.min(Math.max((Math.abs(range) / 100), 0.05), 2);
if (-rate < rangeLimit) {
keyPress(_accelerator);
} else if (-rangeLimit < -rate) {
keyPress(_brake);
}
index++;
setTimeout(A, 200);
}
A();Собственно все. Всем спасибо за прочтение :)

П.С.
Да я немного хайпанул и поприкалывался. Не воспринимайте статью всерьез, я хотел почувствовать себя космонавтом, как Гагарин Юрий Алексеевич… Хотя это скорее инженерная работа Королёва Сергея Павловича, который к сожалению, так и не побывал в космосе, о котором мечтал…